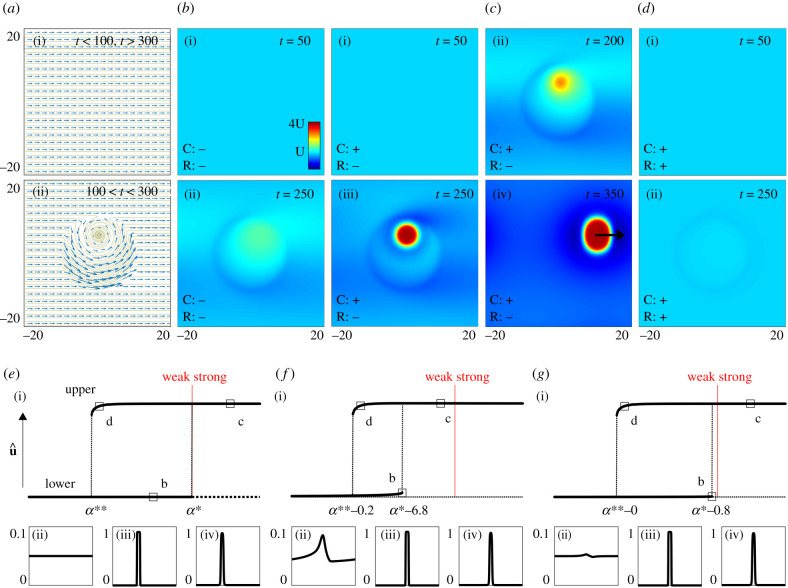
Figure 4.

Dynamics under non-uniform flow. (a) The flow field, w. (b–e) density u (colourscale in (b)(i)). (b) Excluding chemotaxis and rheotaxis (α = ϕ = 0), the population stays unclustered, though non-uniform flow leads to moderate accumulations. (c) Under weak chemotaxis and no rheotaxis (α = 10, ϕ = 0), flow-induced accumulations form into clusters that are sustained following removal of the vortex flow. (d) Addition of rheotaxis (α = 10, ϕ = 1) suppresses the clusters that formed in (c). In (a–d), the population is initially dispersed, u₀(x) = U, v₀(x) = U + ε(x). (e–g) Bifurcation diagrams of numerically determined steady states, u_s(x), represented via $\hat{u}={\text{max}}_{x\in \Omega }(u_s)-{\text{min}}_{x\in \Omega }(u_s)$. Bifurcation parameter is α. Solid branches indicate numerically stable steady states, dotted lines indicate unstable steady states. Representative steady states for the locations indicated by a square shown in below panels. (e) Uniform flow, no rheotaxis (ϕ = 0). (f) Uniform flow, interrupted by a region of slower flow, no rheotaxis (ϕ = 0). (g) As (f), but with rheotaxis (ϕ = 1). Simulations in (a–d) use $\Omega =[-20,20]\times [-20,20]$ and w(x, y, t) = (1, 0) + 0.005(− x − 10y, 10x − y)[tanh (t − 100) − tanh (t − 300)][1 − tanh (0.1x² + 0.1y² − 10)]. Simulations in (e–g) use $\Omega =[-50,50]$ and w(x) = 1.0 + ɛ(1.0 − tanh (x) + tanh (x − 10)), where (e) ɛ = 0, (f–g) ɛ = 0.01. In all simulations, U = 0.05, δ = 1 and ρ = 0.