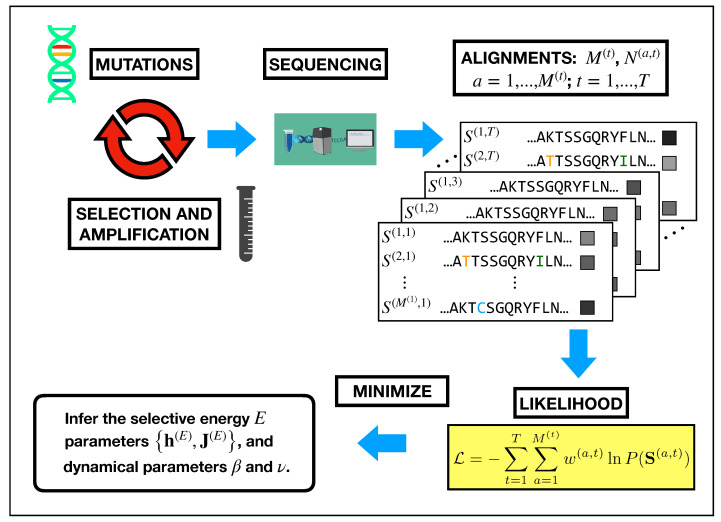
Figure 6.

Pictorial representation of data generation in a Directed Evolution experiment and how they are plugged into the likelihood function to perform the inference. The sequencing of repeated rounds of mutation and selection generates a set of multiple sequence alignments. There, we highlighted with colored letters the sites that have been mutated with respect to the wild-type, coinciding with the first row of the alignment. Moreover, at the right of the sequences, boxes in gray-scale represents the abundances (increasing from black to white). Each sample of sequences $\left\{{\mathit{S}}^{\left(t\right)}\right\}$ and the related abundances $\left\{{\mathit{N}}^{\left(t\right)}\right\}$ for $t=1,\cdots ,T$ are used to define the likelihood function, which subsequently depends only on the parameters to be inferred: ${\mathbf{\theta }}_H=\{{\mathit{h}}^{\left(E\right)},{\mathit{J}}^{\left(E\right)},\mathbf{\nu },\mathbf{\beta }\}$ (see Equations (1)–(3) and (7)). The inference of these parameters is based on the maximization of the log-likelihood. In order to determine the parameters $\mathbf{\beta }$ and $\mathbf{\nu }$, the maximization problem over the energetic parameters is repeated, performing a scan over a set of possible values. Then the pair $({\mathbf{\beta }}_{\mathrm{opt}},{\mathbf{\nu }}_{\mathrm{opt}})$ corresponding to the global maximum of the minus log-likelihood is retained.