Figure 1: Intuition of neural fragility - unbalanced and balanced networks.

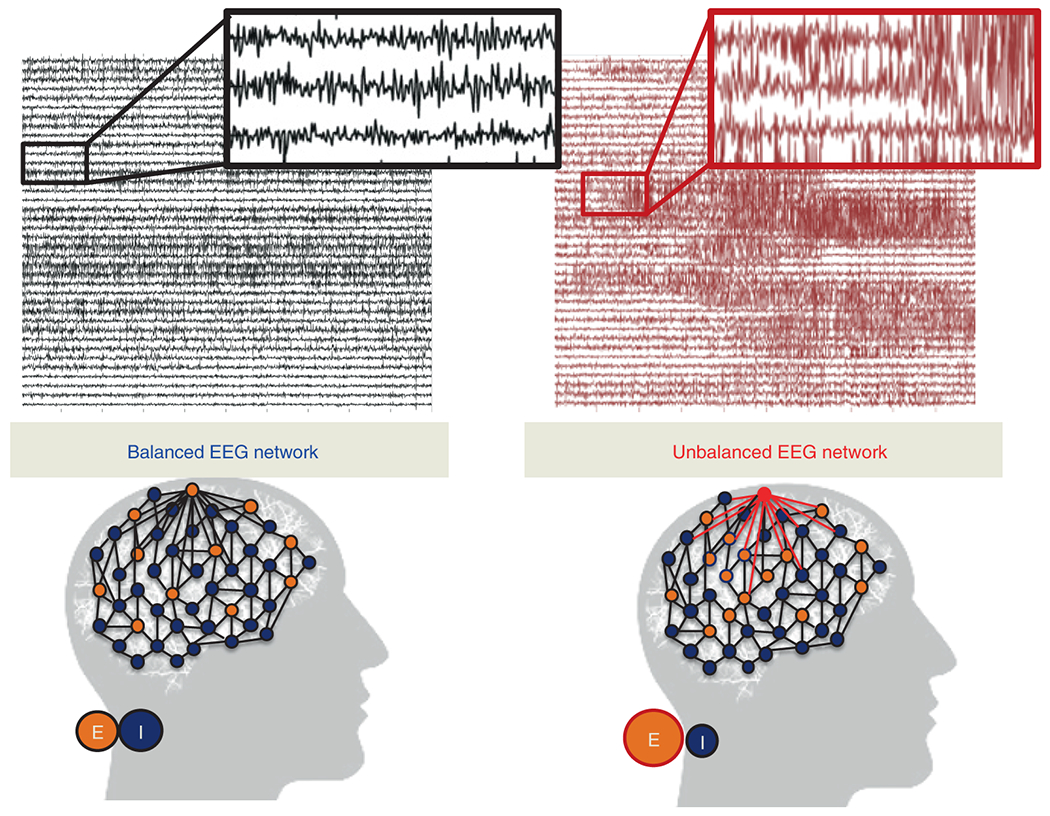
(Top) iEEG traces in between seizures (left) and during a seizure (right). (Bottom) network schematic showing change in connectivity (right) in fragile node that causes seizure. Describes qualitatively the concept of neural fragility in the context of a dynamical iEEG network, with nodes representing excitatory (E) and inhibitory (I) population of neurons. From a dynamical systems point of view, such imbalance arises from a few fragile nodes causing instability of the network in the form of over-excitation, or under-inhibition. We define fragility of a network node to be the minimum-energy perturbation applied to the node’s weights on its neighbors before rendering the network unstable [18, 16]. In systems theory, stable systems return to a baseline condition when a node is perturbed. In contrast, unstable systems can oscillate and grow when a node is perturbed. In the context of epilepsy, a fragile node is one that requires a smaller perturbation to lead to seizure activity. Fragility theory can be modeled in the context of linear dynamical systems: x(t + 1) = Ax(t). Perturbing the columns of the A matrix will alter dynamical connections of a particular node (i.e. that column) on its neighbors, resulting in an imbalanced network.