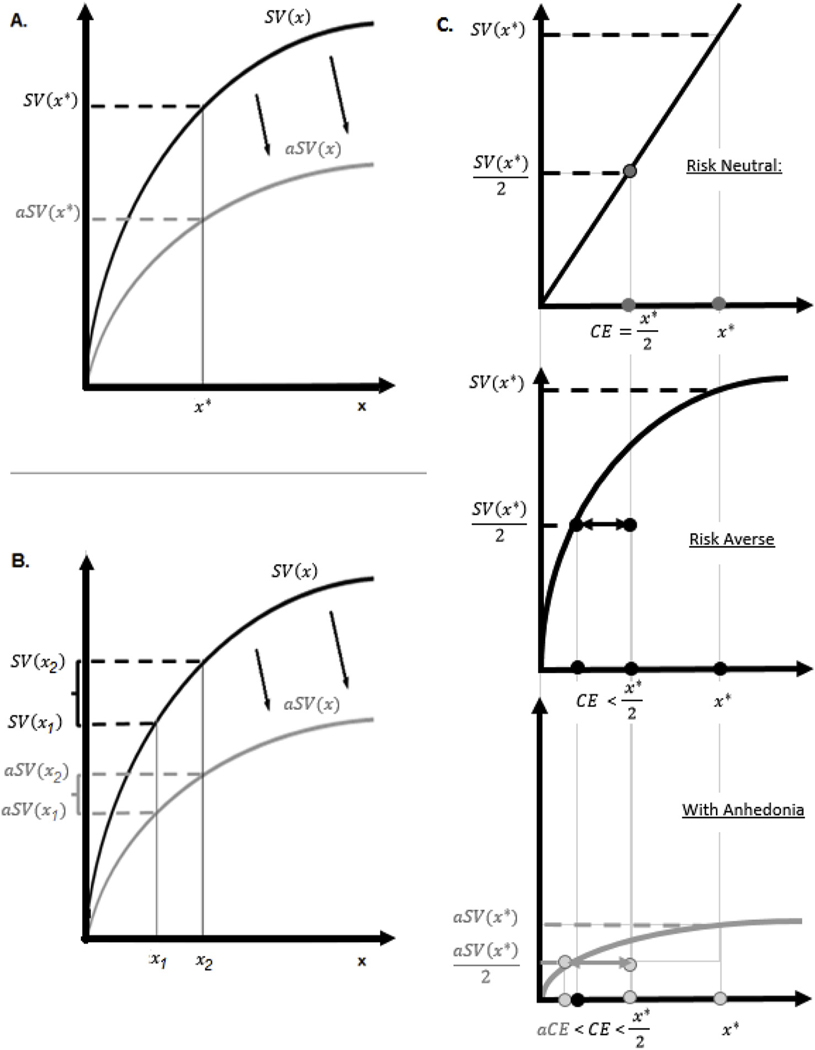
Fig. 1.

Hypothesized effects of Anhedonia on Subjective Value. A. Anhedonia can be operationalized as reduced sensitivity to rewards, which implies flatter subjective value function (aSV). B. For an individual with anhedonia (flatter aSV) the choice between two alternatives, x₁ and x₂, is more difficult than it is for an individual without anhedonia (steeper SV). C. Risk aversion can be operationalized as willingness to pay extra money to avoid dealing with risk. For instance, a risk averse individual may agree to receive $4 with certainty, in preference to a lottery in which there are even odds of receiving $10 or nothing (i.e. with an expected value of $5). The subjective value of such a lottery ($4 in this case) is termed its ‘certainty equivalence’ (CE); the difference between the CE of $4 and the expected value (EV) of $5 is termed the ‘risk premium’ (RP). A risk neutral individual would have a RP of zero, such that the CE = EV; such an individual would not be willing to accept anything less than $5 in exchange for a lottery with an EV of $5. A risk-neutral individual would necessarily have a linear subjective value function (top panel). On the other hand, a concave subjective value function will always yield CE < EV and thus RP > 0, implying risk aversion (middle panel). Flatter subjective value function of an individual with anhedonia implies stronger risk aversion, aCE < CE and thus aRP > RP (bottom panel).