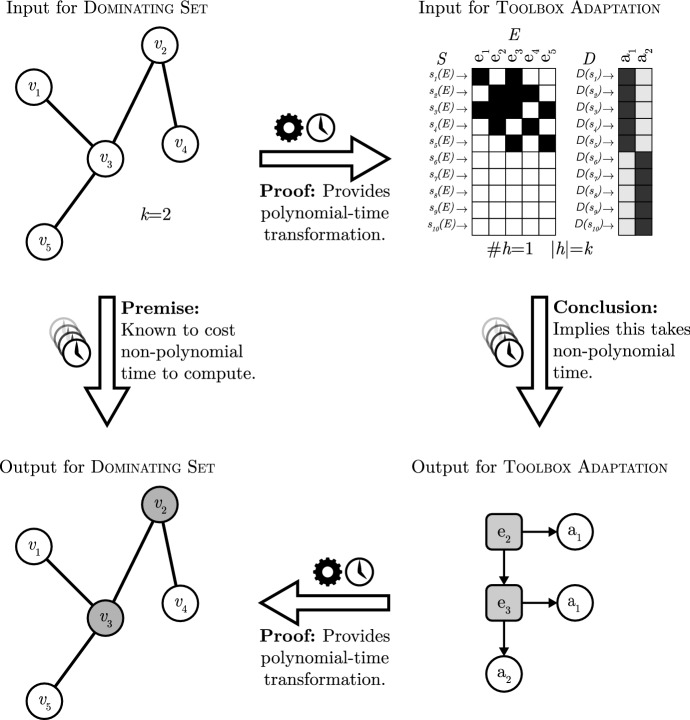
Fig. 7.

An illustration of the proof that Toolbox Adaptation is . Working from the premise that Dominating Set is (and therefore cannot be solved in polynomial time, unless $\mathsf{P}=\mathsf{NP}$), we construct two polynomial-time transformations. One transforms the input for Dominating Set to an input for Toolbox Adaptation, and the other transforms the output of Toolbox Adaptation to an output for Dominating Set. As said, these transformations run in polynomial time and hence we can conclude by contradiction that Toolbox Adaptation cannot run in polynomial time, otherwise one could solve Dominating Set in polynomial time (viz. by transforming the input for Dominating Set, then solving Toolbox Adaptation and then transforming the output back to Dominating Set). Here, the problem Dominating Set is a graph problem that asks whether or not there exists a subset of vertices (maximally of size k) that dominate (are a neighbour of) all other vertices in the graph