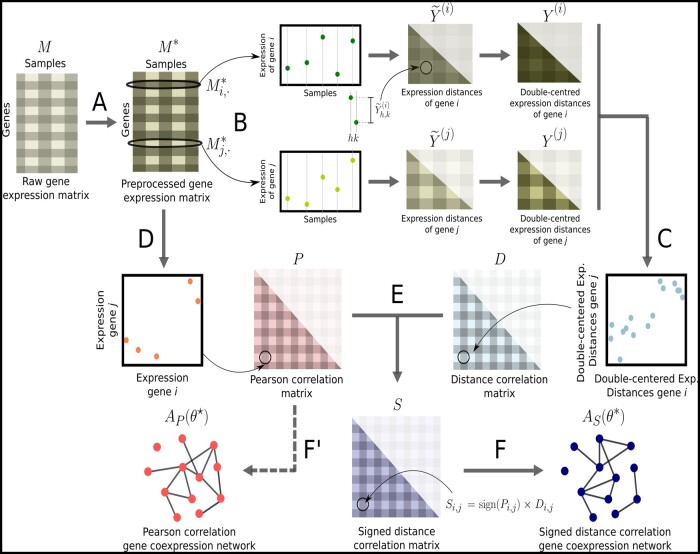
Fig. 1.

Pipeline to construct networks from gene expression data using signed distance correlation. (A) We pre-process the input matrix M with raw gene expression data using quantile normalization and setting the lowest 20% values from each sample to the minimum value in M to obtain $M^{*}$. (B) We compute the expression distance matrices ${\tilde{Y}}^{(i)}$ and ${\tilde{Y}}^{(j)}$ for each gene $i,j\in \{1,\dots ,m\}$, and we double center them to obtain $Y^{(i)}$ and $Y^{(j)}$. (C) We compute the distance correlation matrix D, whose entries $D_{i,j}$ are the positive root of the Pearson correlation between $Y^{(i)}$ and $Y^{(j)}$, for every pair of genes. (D) We compute the Pearson correlation between each pair of rows in the $M^{*}$ to obtain the Pearson correlation matrix P. (E) To construct the signed distance correlation matrix S, we multiply every distance correlation between the expression of two genes $D_{i,j}$ by the sign of their Pearson correlation $\text{sign}(P_{i,j})$. (F) Using COGENT (Bozhilova et al., 2020), we find the optimal threshold ${\theta }^{*}$ that produces the most self-consistent network $A_S({\theta }^{*})$ from S. (F′) Analogously, we find the optimal threshold ${\theta }^{\star }$ to generate the network $A_P({\theta }^{\star })$ from P; this step is not part of the pipeline and only necessary to be able to compare Pearson and signed distance correlation networks.