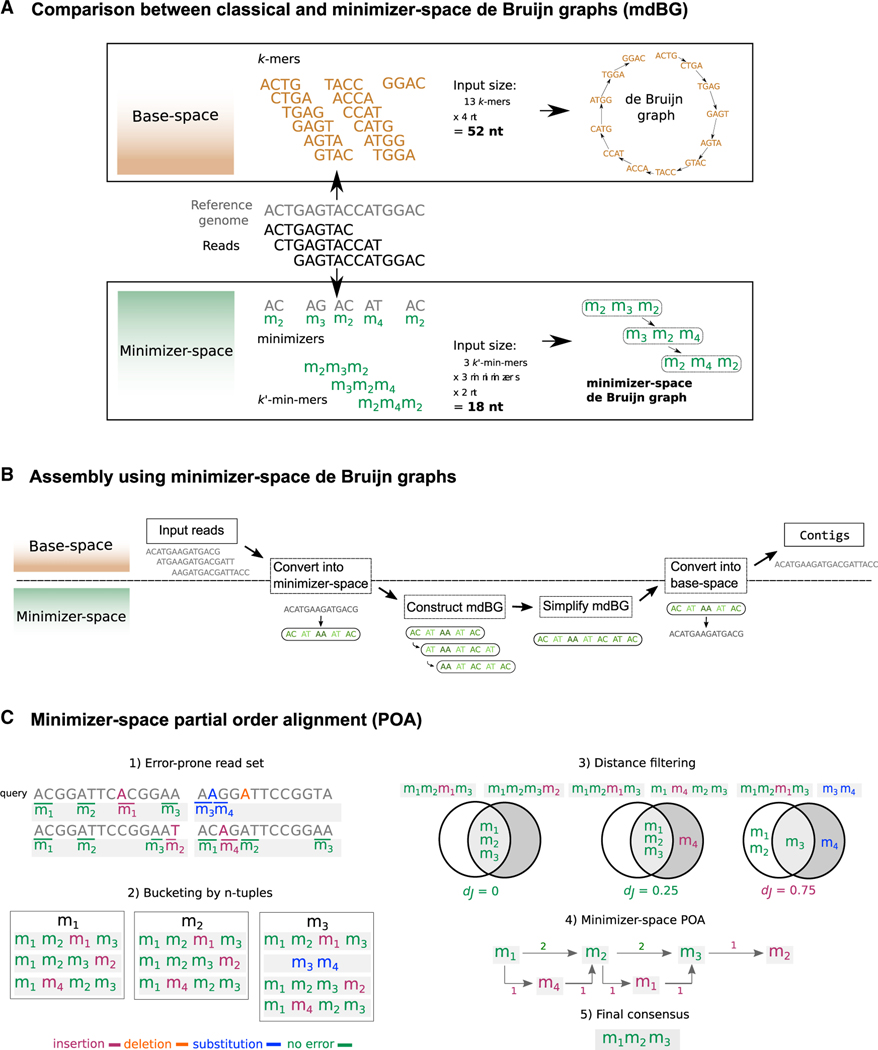
Figure 1. Overview of our methods.
(A) An efficient assembly method for state-of-the-art genome sequencing (e.g., PacBio HiFi data). Illustration of our minimizer-space de Bruijn graph (mdBG, bottom) compared with the original de Bruijn graph (top) commonly used for genome assembly. Center horizontal section shows a toy reference genome, along with a collection of sequencing reads. Top box shows k-mers (k = 4) collected from the reads, which are the nodes of the classical de Bruijn graph. The input size of 52 nucleotides (nt) is depicted in boldface. Bottom box shows the position of minimizers in the reads for = 2, and any -mer starting with nucleotide “A” is chosen as a minimizer. k′-min-mers (using notation k′ = 3 here to differentiate from classical k-mers) are tuples of k′ minimizers as ordered in reads, which constitute the nodes of the minimizer-space de Bruijn graph. Creating k′-min-mers from the minimizer-space representation of reads allows for a reduction in input size, since the only bases stored in a k′-min-mer are the bases of the chosen minimizers. The reduced input size to 18 nucleotides (nt) is depicted in boldface. The minimizer-space representation accelerates the construction and traversal of the de Bruijn graph while reducing memory consumption.
(B) Overview of the assembly pipeline using mdBG. The region of the figure above (respectively, below) the dotted line corresponds to analyses taking place in base space (respectively, minimizer space). The input reads are scanned sequentially, and all [-mers that belong to a pre-selected set of universe minimizers (see STAR Methods) are identified. Each read is then represented as an ordered list of the selected minimizers, and k-min-mers are collected from the minimizer-space representation of reads using a sliding window of length k. A minimizer-space de Bruijn graph (mdBG) is then constructed from the set of all k-min-mers and simplified in order to reduce ambiguity and remove errors. The mdBG is then converted back into base space by concatenating the base-space sequences spanned by the minimizers in the mdBG, and a set of contigs is reported.
(C) Overview of the minimizer-space partial order alignment (POA) procedure with a toy dataset of 4 reads. (1) Error-prone reads and their ordered lists of minimizers ( = 2) are shown, with sequencing errors and the minimizers that are created as a result of errors denoted in colors (insertion as red, deletion as orange, substitution in blue, no errors in green). (2) Before minimizer-space error-correction, the ordered lists of minimizers are bucketed using their n-tuples (n = 1). (3) For a query ordered list (the first read in the read set in the figure), all ordered lists that share an n-tuple with the query are obtained, and the final list of query neighbors are obtained by applying a heuristically determined distance filter dj (Jaccard distance threshold of φ = 0.5). (4) A POA graph in minimizer space is constructed by initializing the graph with the query and aligning each ordered list that passed the filter to the graph iteratively (weights of poorlya supported edges are shown in red). (5) By taking a consensus path of the graph, the error in the query is corrected.