Figure 1.

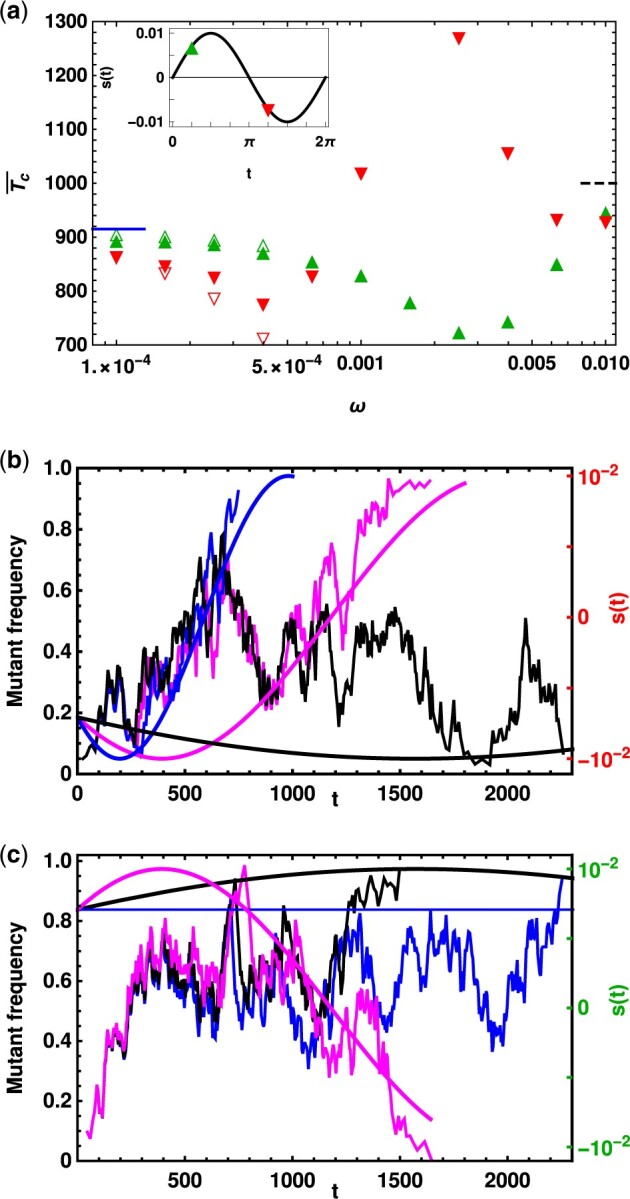
Top panel: Conditional mean fixation time ${\overline{T}}_c$ of a dominant mutant $(h=0.7,▲)$ and a recessive mutant ($h=0.3,▼$) with selection coefficient $s(t)=\sigma \hspace{0.17em}\text{sin}(\omega t+\pi /4)$ and $-s(t)$, respectively [see inset for s(0)] to show that the symmetry between the conditional mean fixation time for dominant beneficial and recessive deleterious mutant in static environments is not preserved in changing environments. The data are obtained by numerical simulations (closed symbols) and numerically integrating the diffusion theory Equations (4) and (5) (open symbols) for small cycling frequencies in a population of size N. The conditional mean fixation time in the static environment with selection $|s(0)|$ (solid line) and in the neutral environment, given by 2 N, (dashed line) are obtained from diffusion theory and shown for comparison. Middle and Bottom panel: Mutant allele trajectories for (b) the initially deleterious mutant (h = 0.3) and cycling frequencies, $\omega =5\times {10}^{-4}(\text{black}),2\times {10}^{-3}(\text{magenta})$, and $4\times {10}^{-3}(\text{blue})$, and (c) the initially beneficial mutant (h = 0.7) for $\omega =0(\text{blue}),5\times {10}^{-4}(\text{black})$, and $2\times {10}^{-3}(\text{magenta})$. The allele trajectories in each panel are almost same at short times as they were started with the same random seed in the computer simulation. The smooth curves show the selection coefficient for the corresponding cycling frequency. In all the panels, $\sigma =0.01$ and N = 500 so that $\alpha =N|s(0)|\approx 3.5$.