Estimation of genetic variance contributed by a quantitative trait locus: correcting the bias associated with significance tests

Abstract

The Beavis effect in quantitative trait locus (QTL) mapping describes a phenomenon that the estimated effect size of a statistically significant QTL (measured by the QTL variance) is greater than the true effect size of the QTL if the sample size is not sufficiently large. This is a typical example of the Winners’ curse applied to molecular quantitative genetics. Theoretical evaluation and correction for the Winners’ curse have been studied for interval mapping. However, similar technologies have not been available for current models of QTL mapping and genome-wide association studies where a polygene is often included in the linear mixed models to control the genetic background effect. In this study, we developed the theory of the Beavis effect in a linear mixed model using a truncated noncentral Chi-square distribution. We equated the observed Wald test statistic of a significant QTL to the expectation of a truncated noncentral Chi-square distribution to obtain a bias-corrected estimate of the QTL variance. The results are validated from replicated Monte Carlo simulation experiments. We applied the new method to the grain width (GW) trait of a rice population consisting of 524 homozygous varieties with over 300 k single nucleotide polymorphism markers. Two loci were identified and the estimated QTL heritability were corrected for the Beavis effect. Bias correction for the larger QTL on chromosome 5 (GW5) with an estimated heritability of 12% did not change the QTL heritability due to the extremely large test score and estimated QTL effect. The smaller QTL on chromosome 9 (GW9) had an estimated QTL heritability of 9% reduced to 6% after the bias-correction.

Introduction

In quantitative trait locus (QTL) linkage mapping and genome-wide association studies (GWAS), an important step is to evaluate the estimated magnitude of the genetic effect at a detected QTL. The estimated magnitude of a QTL is often measured by the variance of the QTL or the proportion of phenotypic variance accounted for by associated variability of allelic effects at the QTL. The latter is also called the QTL heritability. The estimated QTL effect can be positive or negative, but the effect squared is always positive. This squared QTL effect represents the QTL variance. The estimated QTL variance is often biased for two reasons: (1) Wrong statistical models may be used (Allison et al. 2002; Luo et al. 2003; Weller et al. 2005) or (2) Reported QTLs are associated with significance tests (Beavis 1994; Otto and Jones 2000; Goring et al. 2001; Xu 2003). Reporting only significant QTLs is a selection process. The selected QTLs represent a censored “population” and thus the expectation is higher than that of an uncensored population, generating an upward bias in estimates of QTL variance, a phenomenon called the Winners’ curse or the Beavis effect (Beavis 1994; Otto and Jones 2000; Xu 2003; Sun and Bull 2005; Zollner and Pritchard 2007; Zhong and Prentice 2008). The bias can be reduced with an increased sample size, which may not be realistic in practice. The optimal strategy is to correct the bias via statistical treatments, rather than by increasing resources.

Three factors must coexist to generate the Beavis effect: (1) Stringent criterion of significance tests, (2) Small QTL effects, and (3) Small sample sizes. The three factors causing the Beavis effect make the three S property of the Beavis effect. If a reported QTL is very large, the Beavis effect will not take place. Likewise, if the threshold of a test statistic for QTL detection is low (a liberal test), the Beavis effect is also not likely to occur. The Beavis effect cannot be used as a reason to criticize QTLs detected from small samples. Any statistically significant QTLs are legitimate. The very reason we perform statistical tests is to show that a detected QTL is most likely true (with a small P-value). Therefore, a significant QTL is significant, regardless of the sample size. It is the estimated effects of statistically significant QTL that should be carefully examined when the sample size is small. The Beavis effect provides a guideline for a follow-up study in terms of choosing the appropriate sample size to achieve a predetermined statistical power (Huang et al. 2018). The estimated size of a reported QTL may be substantially biased upward if the QTL is detected with an extremely stringent threshold in the test statistic, especially after Bonferroni correction for millions of single-nucleotide polymorphisms (SNPs). The estimated QTL size is often treated as the true QTL size in power calculation and sample size determination for a potential follow-up study. If the sample size is indeed calculated based on the biased QTL size in the follow-up study, the experiment is most likely to fail because the actual true QTL size is smaller. The Beavis effect may have explained many failed follow-up studies in QTL mapping and GWAS (Huang et al. 2018). Therefore, correction for the Beavis effect is an important subject in QTL mapping and association studies.

Goring et al. (2001) suggested that the only way to obtain unbiased estimates of QTL effects is through a validation study that separates the effect estimation stage from the QTL detection stage. Estimation of QTL sizes from an independent sample is not a cost-effective approach. There are alternative approaches that do not need additional experiments. These cost-effective approaches are statistical methods for bias correction. Typical statistical methods include parametric and nonparametric methods. Parametric approaches require knowledge of truncated distributions of the test statistics. Nonparametric approaches, however, are empirical and they mimic the two-stage validation method proposed by Goring et al. (2001). We first review the nonparametric approaches, which were mainly developed by Sun and Bull (2005) and Sun et al. (2011) for QTL detection and extended by Huang et al. (2018) for expression QTL (eQTL) mapping. These methods are called the bootstrap resampling bias reduction (BR-squared) methods. Each bootstrap sample is a subsample randomly extracted with replacement from the full sample. This means that some individuals may occur multiple times while others may not be present at all in a bootstrap sample. QTL are detected from the bootstrap sample. Individuals not selected in the bootstrap sample form an estimation sample from which effects of the detected QTL are estimated. The average estimated QTL effects from a large number of estimation samples (say 1000) are the bias reduced QTL effects. The estimation sample was called the “out-of-sample” in the original publication (Sun and Bull 2005; Sun et al. 2011). The estimation sample mimics an independent validation sample because the observations from the estimation sample are those not included in the bootstrap sample. The estimated QTL effect from the estimation sample serves as an estimated QTL effect from an independent sample. Wu et al. (2005) performed a large scale Monte Carlo simulation experiment to evaluate three bootstrap estimators of QTL effect sizes. Wu et al. (2006) later extended the simulation experiment by directly treating the QTL heritability as the parameter of interest.

The difference between the estimated QTL variances from the bootstrap samples and the estimation samples is the bias. The original estimated QTL variance is subtracted by the bias to give a bias reduced estimate of the QTL variance. The original estimated QTL variance can also be combined with the estimate from the estimation sample to produce a weighted estimate (Sun and Bull 2005; Wu et al. 2005, 2006; Sun et al. 2011). Massive simulation studies showed that the bootstrap estimators correct the bias more efficiently than the cross-validation method (Wu et al. 2005, 2006). The bootstrap methods are computationally challenging if all markers are corrected for the bias. Fortunately, only significant markers need to be corrected for the bias. Sun and Bull (2005) and Sun et al. (2011) published a software package for the BR-squares method. The program was coded in C++ and can easily handle a GWAS with one million SNP markers for a sample as large as 2000 individuals. More applications of the bootstrap methods can be found in the human genetics literature, e.g., GWAS for the time to event trait of Type 1 diabetes (Poirier et al. 2015) in which the authors modified the bootstrap estimators by adjusting for the minor allele frequency of the detected locus.

The parametric methods require the distribution of an estimated QTL effect or a test statistic. If the QTL effect (not the QTL variance) is the parameter to be estimated, a normal distribution is often assumed (Xu 2003; Palmer and Pe’er 2017; Panigrahi et al. 2021). The effect of a detected QTL is considered to be sampled from a truncated normal distribution. The effect that maximizes the truncated normal density is the bias corrected maximum likelihood estimate of the QTL effect (Palmer and Pe’er 2017; Panigrahi et al. 2021). Xiao and Boehnke (2009, 2011) proposed a truncated noncentral t distribution to evaluate and correct the bias of an estimated QTL effect. Xiao and Boehnke (2009) called the method an ascertainment-corrected maximum likelihood method. They developed the method for binary trait QTL mapping first (case-control studies) and then extended the method to QTL mapping for quantitative traits (Xiao and Boehnke 2011).

Within the array of parametric methods, some investigators used the moment method, i.e., equating the expectation of a truncated normal distribution to the observed (estimated) QTL effect or equating the expectation of a truncated noncentral t distribution to the observed t-test statistic (Xu 2003; Xiao and Boehnke 2009, 2011; Palmer and Pe’er 2017; Panigrahi et al. 2021). Other investigators used a conditional maximum likelihood method. For example, Xiao and Boehnke (2009, 2011) maximized the conditional likelihood function to estimate the QTL effect, where the conditional likelihood is the truncated noncentral t probability density. In a case-control study, Zhong and Prentice (2008) presented three estimators for a QTL effect under the truncated normal distribution: (1) the conditional maximum likelihood, (2) the moment method, and (3) the median method. They found that none of the three methods are satisfactory. Therefore, they recommended a weighted approach taking into account the naïve estimate (the original biased estimate) and one of the three estimators.

The actual size of the QTL variance does not tell us whether the QTL is “large or small.” It is the relative size that is more informative. This relative size is the QTL heritability. We cannot directly evaluate the bias in the estimated QTL heritability, but we can evaluate the bias in the estimated QTL variance. Correcting the bias in the estimated QTL heritability has not been studied, although the bootstrap estimators have automatically corrected the biases for any parameters. In this study, we will model the QTL variance and directly correct the QTL variance using a truncated noncentral Chi-square distribution.

Bias correction is available in many previous studies (Luo et al. 2003; Xu 2003; Sun and Bull 2005; Zollner and Pritchard 2007; Zhong and Prentice 2008; Xiao and Boehnke 2009, 2011; Sun et al. 2011; Poirier et al. 2015; Palmer and Pe’er 2017; Huang et al. 2018; Panigrahi et al. 2021), but only for simple models like interval mapping and marker scanning that does not take into account the population structural or the polygenic effect. The current QTL mapping procedures often include a polygenic component to control the genetic background effect (Xu 2013). GWAS methods use linear mixed models (LMM), which include a polygenic component to capture cryptic relationships among individuals (Yu et al. 2006; Kang et al. 2008, 2010; Zhang et al. 2010; Lippert et al. 2011; Zhou and Stephens 2012). Alternative methods for correcting the Beavis effect with complicated models include Monte Carlo simulations and nonparametric methods (Goring et al. 2001; Allison et al. 2002; Sun and Bull 2005; Sun et al.2011; Poirier et al. 2015; Palmer and Pe’er 2017; Huang et al. 2018). It has been suggested that correction for the bias is unsatisfactory and a point estimate from an independent study is the only reliable way to obtain an unbiased estimate of a locus-specific effect (Goring et al. 2001). Conducting more experiments using lines sampled from the same population is a more accurate way to correct the bias (Melchinger et al. 1998), but that approach is not cost effective.

In this study, we propose a new statistical method to correct for the Beavis effect resulting from complicated models that include a polygenic component as a random effect in the linear mixed models. Once again, correcting for the Beavis effect cannot make a significant QTL insignificant; it only changes the estimated QTL variances.

Methods

Following the conventional notation for variables, we use bold face letters to indicate matrices and vectors, and plain face letters to indicate scalars.

The variance of a quantitative trait locus

The single marker model

The simplest model for QTL mapping and GWAS is

$$\mathbf{y}=X\beta +Z\gamma +\mathbf{\epsilon }$$ (1)

where $\mathbf{y}$ is an $n\times 1$ vector of phenotypic values of a quantitative trait and n is the sample size, $\mathbf{X}$ is an $n\times p$ design matrix for p systematic environmental effects (fixed effects, including the intercept) not related to genes and $\mathbf{\beta }$ is a $p\times 1$ vector of the fixed effects, $\mathbf{Z}$ is an $n\times 1$ vector of genotype indicator variable for a locus of interest and $\mathbf{\gamma }$ is the effect of this locus (QTL effect). This QTL effect is a scalar, but this model can be extended to multiple effects. In that case, the QTL effect can be a vector with the number of elements equal to the number of columns in Z. The last term, $\mathbf{\epsilon }$, is an $n\times 1$ vector of residual errors with an assumed $N(0,\mathbf{I}{\sigma }^2)$ distribution, where ${\sigma }^2$ is the residual variance. Model (1) assumes that the trait is controlled by a single locus. Models including multiple loci captured by a polygenic effect will be discussed later. The QTL effect ($\gamma$) is the most important parameter in QTL mapping and GWAS, but it can be negative or positive, depending on how $\mathbf{Z}$ is coded. The absolute value or square of $\gamma$ is a better measurement of the QTL effect size. Ultimately, the size of a QTL must be expressed relative to the residual variance or the phenotypic variance of the trait. Following the classical definition of the QTL effect (Lander and Botstein 1989; Zeng 1994; Falconer and Mackay 1996; Lynch and Walsh 1998; Yu et al. 2006), we treat it as a fixed effect. This makes model (1) a fixed effect model. As a fixed effect model, the expectation and variance are

$$\mathit{E}(\mathbf{y})=X\beta +Z\gamma$$ (2)

and

$$\mathrm{var}(\mathbf{y})=\mathrm{var}(\mathbf{\epsilon })=\mathbf{I}{\sigma }^2,$$ (3)

respectively. The phenotypic variance defined this way does not contain the QTL variance, because the QTL effect is treated as a fixed effect in the linear model. Following the suggestion from the associate editor and a reviewer, we consider $\mathbf{Z}$ as a random variable so that the product $Z_j\gamma$ remains a variable. This allows us to define the variance of $y_j$, i.e., the phenotypic value, by

$$\mathrm{var}(y_j)=\mathrm{var}(Z_j){\gamma }_{}^2+\mathrm{var}({\epsilon }_j)={\sigma }_Z^2{\gamma }_{}^2+{\sigma }^2$$ (4)

The QTL variance is defined as

$${\sigma }_{\mathit{QTL}}^2={\sigma }_Z^2{\gamma }_{}^2$$ (5)

The total phenotypic variance is ${\sigma }_{\mathit{QTL}}^2+{\sigma }^2$ so that the proportion of the phenotypic variance contributed by the QTL, i.e., the QTL heritability, is

$$h_{\mathit{QTL}}^2=\frac{{\sigma }_{\mathit{QTL}}^2}{{\sigma }_{\mathit{QTL}}^2+{\sigma }_{}^2}$$ (6)

The polygenic model

The single marker model is flawed because it considers only one marker and ignores other QTLs throughout the genome. In QTL mapping, effects of other QTL are captured by selected co-factors. Such a method is called composite interval mapping (Jansen and Stam 1994; Zeng 1994). However, fitting a polygenic effect to the model will serve the same purpose as the co-factors in the composite interval mapping (Xu 2013). Fitting a polygene is the common practice in GWAS (Yu et al. 2006). The polygenic model for QTL mapping and GWAS is

$$\mathbf{y}=X\beta +Z\gamma +\mathbf{\xi }+\mathbf{\epsilon }$$ (7)

where $\mathbf{\xi }\sim N(0,\mathbf{K}{\varphi }^2)$ is an $n\times 1$ vector of polygenic effects with an assumed multivariate normal distribution, K is an $n\times n$ normalized covariance structure and ${\varphi }^2$ is the polygenic variance. By normalization, we mean that the sum of the diagonal elements of matrix K equals n, denoted by $\text{tr}(\mathbf{K})=n$, i.e., the trace of K is n. For this model, the phenotypic variance is

$$\mathrm{var}(y_j)=\mathrm{var}(Z_j){\gamma }_{}^2+n^{-1}\mathit{tr}(\mathbf{K}){\varphi }^2+\mathrm{var}({\epsilon }_j)={\sigma }_Z^2{\gamma }_{}^2+{\varphi }^2+{\sigma }^2$$ (8)

Again we define ${\sigma }_{\mathit{QTL}}^2={\sigma }_Z^2{\gamma }_{}^2$ as the QTL variance. The total phenotypic variance is expressed by ${\sigma }_{\mathit{QTL}}^2+{\varphi }^2+{\sigma }^2$ so that the QTL heritability is defined as

$$h_{\mathit{QTL}}^2=\frac{{\sigma }_{\mathit{QTL}}^2}{{\sigma }_{\mathit{QTL}}^2+{\varphi }^2+{\sigma }_{}^2}$$ (9)

The genotype indicator variable ($Z$) is often standardized prior to the data analysis so that ${\mu }_Z=0$, ${\sigma }_Z^2=1$ and

$$h_{\mathit{QTL}}^2=\frac{{\sigma }_{\mathit{QTL}}^2}{{\sigma }_{\mathit{QTL}}^2+{\varphi }^2+{\sigma }_{}^2}=\frac{{\gamma }_{}^2}{{\gamma }_{}^2+{\varphi }^2+{\sigma }_{}^2}$$ (10)

Hereafter, we assume that a standardized $Z$ is used to simplify the presentation of the QTL variance. If the original Z variable is denoted by $Z^{*}$, the standardized Z variable is defined as $Z=(Z^{*}-{\mu }_{Z^{*}})/{\sigma }_{Z^{*}}$, where ${\mu }_{Z^{*}}$ and ${\sigma }_{Z^{*}}$ are the sample mean and sample standard deviation of $Z^{*}$.

Estimation of QTL variance

Although we define ${\sigma }_{\mathit{QTL}}^2={\gamma }^2$, we cannot estimate the QTL variance by ${\widehat{\gamma }}^2$, i.e., ${\widehat{\sigma }}_{\mathit{QTL}}^2\ne {\widehat{\gamma }}^2$, which would be a biased estimate. An unbiased estimate is obtained by treating $\gamma$ as a random effect with a normal distribution, $\gamma \sim N(0,{\sigma }_{\gamma }^2)$, where ${\sigma }_{\gamma }^2$ is the variance of that distribution. For a single random effect, $\gamma$, the variance is defined as ${\sigma }_{\gamma }^2={\gamma }^2$. Therefore, an estimated variance of gamma should be ${\widehat{\sigma }}_{\mathrm{\gamma }}^2=\widehat{{\mathrm{\gamma }}^2}$, which is not ${\widehat{\gamma }}^2$. When ${\sigma }_Z^2=1$, the estimated QTL variance is ${{\widehat{\sigma }}_{\mathit{QTL}}^2=\widehat{\sigma }}_{\mathrm{\gamma }}^2=\widehat{{\mathrm{\gamma }}^2}$. We now propose a moment method (MM) of estimation. Let $\widehat{\gamma }$ be the best linear unbiased estimate (BLUE) of $\gamma$ from model (7) and let $s_{\widehat{\gamma }}^2=\mathrm{var}(\widehat{\gamma }|\gamma )$ be the squared estimation error for $\widehat{\gamma }$. We describe $\widehat{\gamma }$ conditional on $\gamma$ by the following linear model,

$$\widehat{\gamma }=\gamma +e_{\widehat{\gamma }}$$ (11)

where $\gamma \sim N(0,{\sigma }_{\gamma }^2)$ and $e_{\widehat{\gamma }}\sim N(0,s_{\widehat{\gamma }}^2)$. Both $\widehat{\gamma }$ and $s_{\widehat{\gamma }}^2$ are estimated from the data (treated as observed quantities) so that we can evaluate the quadratic form

$${\widehat{\gamma }}^2={(\gamma +e_{\widehat{\gamma }})}^2={\gamma }^2+2\gamma e_{\widehat{\gamma }}+e_{\widehat{\gamma }}^2$$ (12)

The expectation of equation (12) is

$$\mathit{E}({\widehat{\gamma }}^2|\gamma )={\gamma }^2+2\gamma \mathit{E}(e_{\widehat{\gamma }})+\mathit{E}(e_{\widehat{\gamma }}^2)={\sigma }_{\gamma }^2+s_{\widehat{\gamma }}^2$$ (13)

where ${\sigma }_{\gamma }^2={\gamma }^2$, $\mathit{E}(e_{\widehat{\gamma }})=0$ and $\mathit{E}(e_{\widehat{\gamma }}^2)=\mathrm{var}(\widehat{\gamma }|\gamma )=s_{\widehat{\gamma }}^2$. The moment method of estimation for the variance of gamma is obtained by replacing $\mathit{E}({\widehat{\gamma }}^2|\gamma )$ by the observed statistic (${\widehat{\gamma }}^2$) in Equation (13) so that

$${\widehat{\gamma }}^2={\sigma }_{\gamma }^2+s_{\widehat{\gamma }}^2$$ (14)

whose solution for the QTL variance is

$${\widehat{\sigma }}_{\gamma }^2={\widehat{\gamma }}^2-s_{\widehat{\gamma }}^2$$ (15)

A negative estimate is allowed in MM of a variance component. If preferred, we can truncate a negative estimate of the QTL variance at zero, as shown below,

$${\widehat{\sigma }}_{\gamma }^2=\{\begin{array}{c}{\widehat{\gamma }}_{}^2-s_{\widehat{\gamma }}^2\\ 0\end{array}\begin{array}{c}\\ \end{array}\begin{array}{c}\text{if}\\ \text{if}\end{array}\begin{array}{c}\\ \end{array}\begin{array}{c}{\widehat{\gamma }}_{}^2>s_{\widehat{\gamma }}^2\\ {\widehat{\gamma }}_{}^2\le s_{\widehat{\gamma }}^2\end{array}$$ (16)

A statistically more elegant expression of Equation (16) is

$${\widehat{\sigma }}_{\gamma }^2={({\widehat{\gamma }}_{}^2-s_{\widehat{\gamma }}^2)}^{+}$$ (17)

We already assumed that ${\sigma }_Z^2=1$ after standardization and thus

$${\widehat{\sigma }}_{\mathit{QTL}}^2={\sigma }_Z^2{\widehat{\sigma }}_{\gamma }^2={\widehat{\sigma }}_{\gamma }^2={({\widehat{\gamma }}^2-s_{\widehat{\gamma }}^2)}^{+}$$ (18)

Thus, the estimated QTL heritability is rewritten as

$${\widehat{h}}_{\mathit{QTL}}^2=\frac{{\widehat{\sigma }}_{\gamma }^2}{{\widehat{\sigma }}_{\gamma }^2+{\widehat{\varphi }}^2+{\widehat{\sigma }}_{}^2}=\frac{{({\widehat{\gamma }}_{}^2-s_{\widehat{\gamma }}^2)}^{+}}{{({\widehat{\gamma }}_{}^2-s_{\widehat{\gamma }}^2)}^{+}+{\widehat{\varphi }}^2+{\widehat{\sigma }}_{}^2}$$ (19)

In the next section, we will define $s_{\gamma }^2$ as a theoretical value of $s_{\widehat{\gamma }}^2$ while the latter is obtained from the data.

The Beavis effect

An alternative moment estimate of QTL variance

Let $\widehat{\gamma }$ be the estimated QTL effect and define the variance of the estimated effect (squared error) by

$$\mathrm{var}(\widehat{\gamma }|\gamma )=s_{\widehat{\gamma }}^2=\frac{{\widehat{\sigma }}^2}{n_Z{\sigma }_Z^2}=\frac{{\widehat{\sigma }}^2}{n_Z}$$ (20)

where ${\widehat{\sigma }}^2$ is the estimated residual variance, ${\sigma }_Z^2=1$ is the variance of the genotype indicator variable (already standardized prior to the data analysis), and $n_Z$ is defined as

$$n_Z={\mathbf{Z}}^T\mathbf{P}\mathbf{Z}={\mathbf{Z}}^T\left[\mathbf{I}-\mathbf{X}{({\mathbf{X}}^T\mathbf{X})}^{-1}{\mathbf{X}}^T\right]\mathbf{Z}$$ (21)

and

$$\mathbf{P}=\mathbf{I}-\mathbf{X}{({\mathbf{X}}^T\mathbf{X})}^{-1}{\mathbf{X}}^T$$ (22)

We often take the expectation of $n_Z$ with respect to Z so that

$$n_0=\mathit{E}(n_Z\mathit{)=E}({\mathbf{Z}}^T\mathbf{P}\mathbf{Z})=\mathit{E}({\mathbf{Z}}^T)\mathbf{P}\mathit{E}(\mathbf{Z})+\mathit{tr}\left[\mathrm{var}(\mathbf{Z})\mathbf{P}\right]=\mathit{tr}(\mathbf{P})=n-r(\mathbf{X})=n-p$$ (23)

where n is the actual sample size and $r(X)=p$ is the column rank of matrix X. Equation (24) holds because $\mathit{E}(\mathbf{Z})=0$ and $\mathit{var}(\mathbf{Z})=\mathbf{I}$ (Z is a standardized variable). Note that $n_0$ can be interpreted as the residual degree of freedom. When the sample size is sufficiently large, $n_0\approx n$, we may also call $n_0$ the effective sample size. The Wald test statistic is defined as

$$W=\frac{{\widehat{\gamma }}_{}^2}{s_{\widehat{\gamma }}^2}=\frac{n_0{\widehat{\gamma }}_{}^2}{{\widehat{\sigma }}_{}^2}$$ (24)

Under the null model (the QTL effect is zero), the Wald test statistic follows a Chi-square distribution with $k=1$ degree of freedom. Under the alternative model (QTL effect is different from zero), however, the Wald test follows a noncentral Chi-square distribution with a noncentrality parameter $\delta$, which is just the Wald test statistic with the estimated parameters replaced by the true parameters, i.e.,

$$\delta =\frac{{\gamma }^2}{s_{\gamma }^2}=\frac{n_0{\gamma }^2}{{\sigma }^2}$$ (25)

where

$$s_{\gamma }^2=\frac{ {\sigma }^2}{n_0}$$

is the theoretical value of the squared estimation error of $\widehat{\gamma }$. Define the QTL variance by ${\sigma }_{\gamma }^2={\gamma }^2$. The noncentrality parameter is rewritten as

$$\delta =\frac{n_0{\gamma }^2}{{\sigma }^2}=\frac{n_0{\sigma }_{\gamma }^2}{{\sigma }^2}$$ (26)

Under the alternative hypothesis, the expectation of the Wald test statistics (noncentral Chi-square variable) is

$$\mathit{E}(W)=\mathit{E}\left[{\chi }_k^2(\delta )\right]=\delta +k=n_0{\sigma }_{\gamma }^2/{\sigma }^2+k$$ (27)

where $k=1$ and ${\chi }_k^2(\delta )$ is an alternative notation for ${\chi }_{}^2(k,\delta )$, a noncentral Chi-square distribution with $k=1$ degrees of freedom and a noncentrality parameter $\delta$. Equation (28) allows us to estimate the QTL variance using the moment method, which is obtained by substituting the expectations of variables in an equation by the observations of the variables and solving for the parameter of interest. The moment estimate of the QTL variance is obtained by solving the following equation

$$W=\frac{n_0{\sigma }_{\gamma }^2}{{\widehat{\sigma }}^2}+1$$ (28)

The solution for ${\sigma }_{\gamma }^2$ is

$${\widehat{\sigma }}_{\gamma }^2=\frac{{\widehat{\sigma }}^2}{n_0}(W-1)$$ (29)

If a negative estimate is not allowed, we simply truncate the negative estimate at zero. This is an alternative moment method of estimation for the QTL variance. Further simplification shows that Equation (30) is identical to Equation (17),

$${\widehat{\sigma }}_{\gamma }^2=\frac{{\widehat{\sigma }}^2}{n_0}{(W-1)}^{+}=s_{\widehat{\gamma }}^2{\left(\frac{{\widehat{\gamma }}^2}{s_{\widehat{\gamma }}^2}-1\right)}^{+}={({\widehat{\gamma }}^2-s_{\widehat{\gamma }}^2)}^{+}$$ (30)

Theoretical bias in QTL variance after application of a significance test

QTLs not detected are excluded and thus reported QTLs form a hypothetical sample of censored data. Equation (30) is the key to evaluate the bias in the estimated QTL variance. Let us replace W by the expectation of a truncated noncentral Chi-square distribution with one degree of freedom,

$${\sigma }_{\gamma }^{2(\text{BIASED})}=\frac{{\sigma }^2}{n_0 }\left[\mathit{E}(W|W>t_W)-1\right]$$ (31)

where $t_W$ is the critical value of the Wald test above which the locus is claimed to be significant. The estimated QTL variance of a reported QTL should be biased upward because $W>t_W$ follows a truncated noncentral Chi-square distribution (Marchand 1996; Li and Yu 2009). Let us replace $W$ by ${\chi }_k^2(\delta )$, a variable from a noncentral Chi-square distribution with a degree of freedom $k=1$ and a noncentrality parameter of $\delta$. We now have

$${\sigma }_{\gamma }^{2(\text{BIASED})}=\frac{{\sigma }^2}{n_0}\left\{\mathit{E}\left[{\chi }_1^2(\delta )|{\chi }_1^2(\delta )>t_W\right]-1\right\}$$ (32)

Recall that $\delta =n_0{\sigma }_{\gamma }^2/{\sigma }^2$. The noncentral Chi-square variable is a function of the true QTL variance,

$${\chi }_1^2(\delta )={\chi }_1^2(n_0{\sigma }_{\gamma }^2/{\sigma }^2)$$ (33)

Substituting this variable into Equation (33) leads to

$${\sigma }_{\gamma }^{2(\text{BIASED})}=\frac{{\sigma }^2}{n_0}\left\{\mathit{E}\left[{\chi }_1^2(n_0{\sigma }_{\gamma }^2/{\sigma }^2)|{\chi }_1^2(n_0{\sigma }_{\gamma }^2/{\sigma }^2)>t_W\right]-1\right\}$$ (34)

where ${\sigma }_{\gamma }^2$ in the right hand side of this equation is the true QTL variance and ${\sigma }_{\gamma }^{2(\text{BIASED})}$ in the left hand side of this equation is the biased QTL variance. This equation allows us to evaluate the theoretical bias given the effective sample size ($n_0$), the residual error variance (${\sigma }^2$), and the true QTL variance (${\sigma }_{\gamma }^2$).

Correcting the bias

Substituting ${\sigma }_{\gamma }^{2(\text{BIASED})}$ and ${\sigma }^2$ in Equation (35) by ${\widehat{\sigma }}_{\gamma }^{2(\text{BIASED})}$ and ${\widehat{\sigma }}^2$, the estimated values from the data, we have

$${\widehat{\sigma }}_{\gamma }^{2(\mathit{BIASED})}=\frac{{\widehat{\sigma }}^2}{n_0}\left\{\mathit{E}\left[{\chi }_1^2(n_0{\sigma }_{\gamma }^2/{\widehat{\sigma }}^2)|{\chi }_1^2(n_0{\sigma }_{\gamma }^2/{\widehat{\sigma }}^2)>t_W\right]-1\right\}$$ (35)

After rearrangement of the equation, we obtain

$$\mathit{E}\left[{\chi }_1^2(n_0{\sigma }_{\gamma }^2/{\widehat{\sigma }}^2)|{\chi }_1^2(n_0{\sigma }_{\gamma }^2/{\widehat{\sigma }}^2)>t_W\right]=\frac{n_0{\widehat{\sigma }}_{\gamma }^{2(\text{BIASED})}}{{\widehat{\sigma }}^2}+1$$ (36)

The right hand side of the equation is

$$\frac{n_0{\widehat{\sigma }}_{\gamma }^{2(\text{BIASED})} }{{\widehat{\sigma }}^2}+1=\frac{n_0({\widehat{\gamma }}^2-s_{\widehat{\gamma }}^2) }{{\widehat{\sigma }}^2}+1=\frac{n_0{\widehat{\gamma }}^2 }{{\widehat{\sigma }}^2}-\frac{n_0{s}_{\widehat{\gamma }}^2 }{{\widehat{\sigma }}^2}+1=W$$ (37)

where $n_0{\widehat{\gamma }}^2/{\widehat{\sigma }}^2=W$, $s_{\widehat{\gamma }}^2={\widehat{\sigma }}^2/n_0$ and $n_0{s}_{\widehat{\gamma }}^2/{\widehat{\sigma }}^2=1$. Therefore, Equation (37) becomes

$$\mathit{E}\left[{\chi }_1^2({\sigma }_{\gamma }^2/s_{\widehat{\gamma }}^2)|{\chi }_1^2({\sigma }_{\gamma }^2/s_{\widehat{\gamma }}^2)>t_W\right]=W$$ (38)

Let the expectation of the truncated noncentral Chi-square distribution in the left hand side of Equation (39) be

$$f({\sigma }_{\gamma }^2)=\mathit{E}\left[{\chi }_1^2({\sigma }_{\gamma }^2/s_{\widehat{\gamma }}^2)|{\chi }_1^2({\sigma }_{\gamma }^2/s_{\widehat{\gamma }}^2)>t_W\right]$$ (39)

which is a function of the QTL variance. Equation (39) can be rewritten as

$$f({\sigma }_{\gamma }^2)=W$$ (40)

The solution for ${\sigma }_{\gamma }^2$ is implicit, requiring an initial value of the parameter and taking a few iterations to converge. The final solution is denoted by

$${\widehat{\sigma }}_{\gamma }^{2(\text{CORRECTED})}=\underset{{\sigma }_{\gamma }^2}{\arg }\left[f({\sigma }_{\gamma }^2)=W\right]$$ (41)

Analysis of the polygenic model

The Beavis effect and correction for the Beavis effect described previously apply to the single marker model. We now extend the analysis to a polygenic model, which is the default model for GWAS (Yu et al. 2006; Zhang et al. 2010). QTL mapping can also use the polygenic model to control the genetic background (Xu 2013). The linear mixed model is

$$\mathbf{y}=X\beta +Z\gamma +\mathbf{\xi }+\mathbf{\epsilon }$$ (42)

The expectation of y is $\mathrm{E}(\mathbf{y})=X\beta +Z\gamma$ and the variance-covariance matrix of y is

$$\mathrm{var}(\mathbf{y})=\mathbf{V}=\mathrm{var}(\mathbf{\xi })+\mathrm{var}(\mathbf{\epsilon })=\mathbf{K}{\varphi }^2+\mathbf{I}{\sigma }^2=(\mathbf{K}\lambda +\mathbf{I}){\sigma }^2=\mathbf{H}{\sigma }^2$$

where $\lambda ={\varphi }^2/{\sigma }^2$ is the variance ratio (proportional to the size of the polygene) and

$$\mathbf{H}=\mathbf{K}\lambda +\mathbf{I}$$ (43)

which is the covariance structure of the mixed model. The variance parameters can be estimated from the restricted maximum likelihood (REML) method (Patterson and Thompson 1971). Once the parameters are estimated, the best linear unbiased estimates (BLUE) of the fixed effects ($\mathbf{\beta }$ and $\mathbf{\gamma }$) are obtained from the following equations,

$$\left[\begin{array}{c}\widehat{\mathbf{\beta }}\\ \widehat{\mathbf{\gamma }}\end{array}\right]={\left[\begin{array}{cc}{\mathbf{X}}^T{\mathbf{H}}^{-1}\mathbf{X}& {\mathbf{X}}^T{\mathbf{H}}^{-1}{\mathbf{Z}}_{}\\ {\mathbf{Z}}_{}^T{\mathbf{H}}^{-1}\mathbf{X}& {\mathbf{Z}}_{}^T{\mathbf{H}}^{-1}{\mathbf{Z}}_{}\end{array}\right]}^{-1}\left[\begin{array}{c}{\mathbf{X}}^T{\mathbf{H}}^{-1}\mathbf{y}\\ {\mathbf{Z}}^T{\mathbf{H}}^{-1}\mathbf{y}\end{array}\right]$$ (44)

The variance-covariance matrix of the BLUE is

$$\mathrm{var}\left[\begin{array}{c}\widehat{\mathbf{\beta }}\\ \widehat{\mathbf{\gamma }}\end{array}\right]={\left[\begin{array}{cc}{\mathbf{X}}^T{\mathbf{H}}^{-1}\mathbf{X}& {\mathbf{X}}^T{\mathbf{H}}^{-1}{\mathbf{Z}}_{}\\ {\mathbf{Z}}_{}^T{\mathbf{H}}^{-1}\mathbf{X}& {\mathbf{Z}}_{}^T{\mathbf{H}}^{-1}{\mathbf{Z}}_{}\end{array}\right]}^{-1}{\widehat{\sigma }}^2=\left[\begin{array}{cc}{\mathbf{C}}_{XX}& {\mathbf{C}}_{XZ}\\ {\mathbf{C}}_{ZX}& {\mathbf{C}}_{ZZ}\end{array}\right]{\widehat{\sigma }}^2$$ (45)

Define

$$\mathbf{P}={\mathbf{H}}^{-1}-{\mathbf{H}}^{-1}\mathbf{X}{({\mathbf{X}}^T{\mathbf{H}}^{-1}\mathbf{X})}^{-1}{\mathbf{X}}^T{\mathbf{H}}^{-1}$$

The variance of the estimated QTL effect is

$$\mathrm{var}(\widehat{\gamma }|\gamma )=s_{\widehat{\gamma }}^2={\mathbf{C}}_{ZZ}{\widehat{\sigma }}^2=\frac{{\widehat{\sigma }}^2}{{\mathbf{Z}}^T\mathbf{P}\mathbf{Z}}=\frac{{\widehat{\sigma }}^2}{n_Z}$$ (46)

The expectation of $n_Z$ with respect to Z is

$$n_0=\mathit{E}({\mathbf{Z}}^T\mathbf{P}\mathbf{Z})=\mathit{E}({\mathbf{Z}}^T)\mathbf{P}\mathit{E}(\mathbf{Z})+\mathit{tr}\left[\mathrm{var}(\mathbf{Z})\mathbf{P}\right]=\text{tr}(\mathbf{P})$$

because $\mathrm{E}(\mathbf{Z})=0$ and $\mathrm{var}(\mathbf{Z})=\mathbf{I}$ (Z has been standardized prior to the data analysis). We replace Equation (47) by

$$s_{\widehat{\gamma }}^2=\frac{{\widehat{\sigma }}^2}{\mathit{E}({\mathbf{Z}}^T\mathbf{P}\mathbf{Z})}=\frac{{\widehat{\sigma }}^2}{n_0}$$ (47)

The theoretical value of the variance is

$$s_{\gamma }^2=\frac{{\sigma }^2}{\mathit{E}({\mathbf{Z}}^T\mathbf{P}\mathbf{Z})}=\frac{{\sigma }^2}{\mathit{tr}(\mathbf{P})}=\frac{{\sigma }^2}{n_0}$$ (48)

When there are no fixed effects other than the grand mean, the effective sample size can be approximated via

$$n_0=\mathit{tr}(\mathbf{P})\approx \mathit{tr}({\mathbf{H}}^{-1})=\mathit{tr}\left[\mathbf{U}{(\lambda \mathbf{D}+\mathbf{I})}^{-1}{\mathbf{U}}^T\right]=\mathit{tr}\left[{(\lambda \mathbf{D}+\mathbf{I})}^{-1}\right]$$ (49)

where $\mathbf{D}=\text{diag}\left\{\begin{array}{cccc}{d}_1& d_2& \cdots & d_n\end{array}\right\}$ holds the eigenvalues of the kinship matrix K and U are the eigenvectors of K. Because D is a diagonal matrix, the effective sampled size is rewritten as

$$n_0\approx \mathit{tr}\left[{(\lambda \mathbf{D}+\mathbf{I})}^{-1}\right]=\sum _{j=1}^n{(\lambda d_j+1)}^{-1}$$ (50)

The Wald test statistic is defined as

$$W=\frac{{\widehat{\gamma }}_{}^2}{s_{\widehat{\gamma }}^2}=\frac{n_0{\widehat{\gamma }}_{}^2}{{\widehat{\sigma }}_{}^2}$$ (51)

The biased QTL variance incorporating the Beavis effect is

$${\sigma }_{\gamma }^{2(\text{BIASED})}=\frac{{\sigma }^2}{n_0}\left[\mathit{E}(W|W>t_W)-1\right]=\frac{{\sigma }^2}{n_0}\left\{\mathit{E}\left[{\chi }_1^2({\sigma }_{\gamma }^2/s_{\gamma }^2)|{\chi }_1^2({\sigma }_{\gamma }^2/s_{\gamma }^2)>t_W\right]-1\right\}$$ (52)

The ${\sigma }_{\gamma }^2$ in the right hand side of the equation is the theoretical value of the QTL variance and the ${\sigma }_{\gamma }^{2(\text{BIASED})}$ in the left hand side of the equation is the theoretically biased QTL variance.

To correct the bias, Equation (39) for the single QTL model applies to the polygenic model,

$$\mathit{E}\left[{\chi }_1^2(\delta )|{\chi }_1^2(\delta )>t_W\right]-W=0$$ (53)

where $\delta ={\sigma }_{\gamma }^2/s_{\widehat{\gamma }}^2$. Again, the solution for the noncentrality parameter is not explicit and, with an initial value of $\delta$, a few iterations are required to achieve the final bias corrected solution, denoted by $\widehat{\delta }$. The bias corrected estimate of the QTL variance is

$${\widehat{\sigma }}_{\gamma }^{2(\text{CORRECTED})}=s_{\widehat{\gamma }}^2\widehat{\delta }$$ (54)

where $\widehat{\delta }$ is the solution from Equation (54) and $s_{\widehat{\gamma }}^2$ is obtained from Equation (48).

Technical improvement

In analysis of experimental data, correction for the bias may not be as easy as that given in Equation (54). To calculate the noncentrality parameter after truncation on the Wald test statistic, Li and Yu (2009) proposed a modified moment method of estimation using a single value of the Wald test statistic ($W$). Let ${\alpha }_W$ be a number $0<{\alpha }_W<1$ and the following value is recommended (Li and Yu 2009)

$${\alpha }_W=(t_W+2)/(t_W+2+k)$$ (55)

where $k=1$ is the degree of freedom of the Wald test. Define

$$J(0)=\mathit{E}\left[{\chi }_1^2(0)|{\chi }_1^2(0)>t_W\right]$$ (56)

as the expectation of the truncated central Chi-square distribution with 1 degree of freedom. Let

$${\kappa }_{\alpha }=\min \left\{{\delta }_{TM}(W)={\alpha }_W(\kappa -t_W),\kappa \ge J(0)\right\}$$ (57)

i.e., ${\kappa }_{\alpha }$ is the minimum solution of ${\delta }_{TM}(W)={\alpha }_W(\kappa -t_W)$ when $\kappa \ge J(0)$. The modified estimate of the noncentrality parameter is

$${\widehat{\delta }}_{\alpha }(W)=\{\begin{array}{c}{\alpha }_W(W-t_W)\\ {\delta }_{TM}(W)\end{array}\begin{array}{c}\\ \end{array}\begin{array}{c}\text{for}\\ \text{for}\end{array}\begin{array}{c}\\ \end{array}\begin{array}{c}{t}_W<W\le {\kappa }_{\alpha }\\ W>{\kappa }_{\alpha }\end{array}$$ (58)

where ${\delta }_{TM}(W)$ is the moment estimate of the noncentrality parameter satisfying

$$\mathit{E}\left\{{\chi }_1^2\left[{\delta }_{TM}(W)\right]|{\chi }_1^2\left[{\delta }_{TM}(W)\right]>t_W\right\}=W$$ (59)

The bias corrected estimate of the QTL variance is

$${\widehat{\sigma }}_{\gamma }^{2(\text{CORRECTED})}=s_{\widehat{\gamma }}^2{\widehat{\delta }}_{\alpha }(W)$$ (60)

Results

An example

Biased QTL heritability

Assume that the true QTL variance is ${\sigma }_{\gamma }^2=2$ so that the QTL effect is $\gamma =\sqrt{2}=1.4142$. Assume that the residual variance is ${\sigma }^2=10$. The QTL heritability is $h_{\mathit{QTL}}^2={\sigma }_{\gamma }^2/({\sigma }_{\gamma }^2+{\sigma }^2)=2/(2+10)=0.1667$. Assume that the sample size is $n_0=100$ and the threshold of the Wald test is $t_W=20$. We now have enough information to evaluate the theoretical bias in the estimated QTL variance and QTL heritability. The noncentrality parameter is $\delta =n_0{\sigma }_{\gamma }^2/{\sigma }^2=100\times 2/10=20$. The expectation of the truncated Chi-square distribution is

$$\mathit{E}\left[{\chi }_1^2(\delta )|{\chi }_1^2(\delta )>t_W\right]=\mathit{E}\left[{\chi }_1^2(20)|{\chi }_1^2(20)>20\right]=28.1365$$

The biased QTL variance (theoretically) is

$${\sigma }_{\gamma }^{2(\text{BIASED})}=\frac{{\sigma }^2}{n_0}\left\{\mathit{E}\left[{\chi }_1^2(\delta )|{\chi }_1^2(\delta )>t_W\right]-1\right\}=\frac{10}{100}\times \left(28.1365-1\right)=2.71365$$

The actual bias of the QTL variance is ${\sigma }_{\gamma }^{2(\text{BIASED})}-{\sigma }_{\gamma }^2=2.71365-2=0.71365$. The theoretical biased heritability is

$$h_{\mathit{QTL}}^{2(\text{BIASED})}={\sigma }_{\gamma }^{2(\text{BIASED})}/({\sigma }_{\gamma }^{2(\text{BIASED})}+{\sigma }^2)=2.71365/(2.71365+10)=0.2134438$$

The actual bias in QTL heritability is

$$h_{\mathit{QTL}}^{2(\text{BIASED})}-h_{\mathit{QTL}}^2=0.2134438-0.1667=0.04677713$$

The relative bias in QTL heritability is

$$(h_{\mathit{QTL}}^{2(\text{BIASED})}-h_{\mathit{QTL}}^2)/h_{\mathit{QTL}}^2=0.04677713/0.1667=28\%.$$

Correcting the bias

Assume that the sample size is $n_0=100$ and the threshold in the Wald test is $t_W=20$. A QTL has passed the criterion of the test. Assume that the estimated QTL variance is ${\widehat{\sigma }}_{\gamma }^{2(\text{BIASED})}=2.71365$ and the estimated residual variance is ${\widehat{\sigma }}^2=10$. The estimated QTL heritability is then

$${\widehat{h}}_{\mathit{QTL}}^{2(\text{BIASED})}={\widehat{\sigma }}_{\gamma }^{2(\text{BIASED})}/({\widehat{\sigma }}_{\gamma }^{2(\text{BIASED})}+{\widehat{\sigma }}^2)=0.2134438$$

The squared error of the estimated QTL effect is $s_{\widehat{\gamma }}^2={\widehat{\sigma }}^2/n_0=10/100=0.1$. Therefore, the retrospective estimated QTL effect is

$${\widehat{\gamma }}^2={\widehat{\sigma }}_{\gamma }^2+s_{\widehat{\gamma }}^2=2.71365+0.1=2.81365.$$

The retrospective Wald test is

$$W=\frac{{\widehat{\gamma }}^2}{s_{\widehat{\gamma }}^2}=\frac{2.81365}{0.1}=28.1365$$

Since the reported QTL variance is associated with a test statistic, there is a bias. We are now ready to correct the bias using the following equation

$$\mathit{E}\left[{\chi }_1^2({\sigma }_{\gamma }^2/s_{\widehat{\gamma }}^2)|{\chi }_1^2({\sigma }_{\gamma }^2/s_{\widehat{\gamma }}^2)>t\right]=W$$

which is simplified into

$$\mathit{E}\left[{\chi }_1^2(10{\sigma }_{\gamma }^2)|{\chi }_1^2(10{\sigma }_{\gamma }^2)>20\right]=28.1365$$

Let $\delta =10{\sigma }_{\gamma }^2$, so that the above equation is rewritten into

$$\mathit{E}\left[{\chi }_1^2(\delta )|{\chi }_1^2(\delta )>20\right]=28.1365$$

Solving for $\delta$ numerically, we have $\widehat{\delta }=20$ and thus the bias corrected QTL variance is

$${\widehat{\sigma }}_{\gamma }^{2(\text{CORRECTED})}=s_{\widehat{\gamma }}^2\widehat{\delta }=0.1\times 20=2$$

which is the original QTL variance presented in the previous section. Of course, the bias corrected QTL heritability is

$${\widehat{h}}_{\mathit{QTL}}^{2(\text{CORRECTED})}={\widehat{\sigma }}_{\gamma }^{2(\text{CORRECTED})}/({\widehat{\sigma }}_{\gamma }^{2(\text{CORRECTED})}+{\widehat{\sigma }}^2)=2/(2+10)=0.1667$$

which is also shown in the previous section.

Simulation for QTL mapping

The simplest model was chosen for QTL mapping. There was no genetic background to control (mimicking the simple interval mapping). We assume that the marker is in perfect LD with the QTL and thus genotypes of the QTL are assumed to be observed. The genotypes of the QTL were sampled from a multinomial distribution with three categories, mimicking the A, H, and B genotypes of an F₂ population with 0.25, 0.5, and 0.25 genotypic frequencies, respectively. The numerical code for the three genotypes is 1, 0, or −1, respectively, corresponding to the additive model. The numerical genotype was standardized prior to the data analysis. We assumed the residual error variance to be ${\sigma }^2=20$ and the trait mean to be $\mu =100$. The QTL variance and thus the QTL effect were determined by the QTL heritability, which varied from 0 to 0.5 incremented by 0.005. Given $h_{\mathit{QTL}}^2={\sigma }_{\gamma }^2/({\sigma }_{\gamma }^2+{\sigma }^2)$, we get

$${\sigma }_{\gamma }^2=h_{\mathit{QTL}}^2({\sigma }_{\gamma }^2+{\sigma }_{}^2)=h_{\mathit{QTL}}^2{\sigma }_{\gamma }^2+h_{\mathit{QTL}}^2{\sigma }_{}^2$$ (61)

Rearranging the above equation leads to

$${\sigma }_{\gamma }^2={\sigma }_{}^2{h}_{\mathit{QTL}}^2/(1-h_{\mathit{QTL}}^2)$$

The QTL effect is

$$\gamma =\sqrt{{\sigma }_{\gamma }^2}=\sigma \sqrt{h_{\mathit{QTL}}^2/(1-h_{\mathit{QTL}}^2)}$$ (62)

The phenotypic value of an individual was simulated from

$$y_j=\mu +Z_j\gamma +{\epsilon }_j$$ (63)

where $Z_j$ is the standardized genotypic code for individual j and ${\epsilon }_j$ is the residual effects sampled from the $N(0,{\sigma }^2)$ distribution. The sample size (n) was set at four levels, 100, 200, 300, and 400. The threshold ($t_W$) for the Wald test was arbitrarily set at six levels, 0, 5, 10, 15, 20, and 25, where $t_W=0$ indicates no significance test (no Beavis effect was expected). Each experimental setup was replicated 40 times and the average estimated QTL heritability was compared to the theoretical value calculated from Equation (35). The bias-corrected heritability was obtained by solving Equation (39) or Equation (41).

Biased QTL heritability

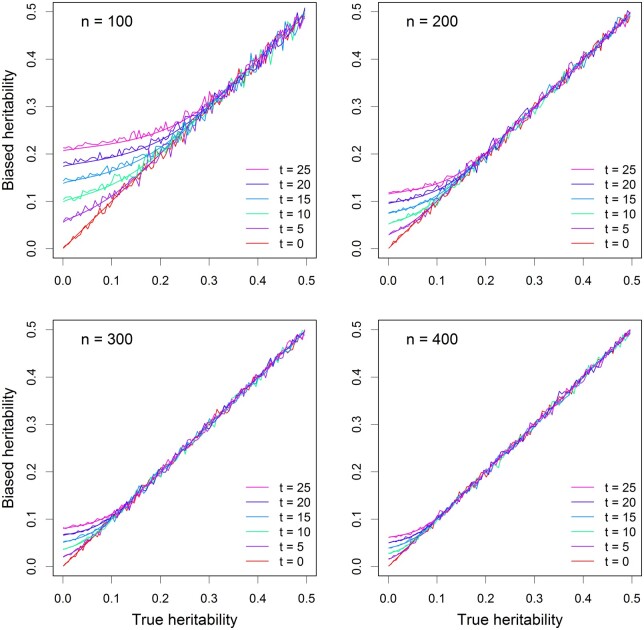
Figure 1 shows the average estimated QTL heritability (noisy curves) of 40 replicates and the theoretically predicted heritability (smooth curves) plotted against the true QTL heritability. The heritability ranges from 0 to 0.5. As the heritability increases, the bias (deviation from the diagonal) becomes smaller (closer to the diagonal). The bias decreases as the sample size (n) increases. The bias also increases as the threshold ($t_W$) increases. The simulation results behave exactly as predicted from the theory.

Figure 1.

Comparison of estimated QTL heritability with true QTL heritability from replicated simulation experiments. There are four different sample sizes (n) and six different thresholds of test statistics (t). The simple linear model (without polygenic background control) was used in the simulation experiments. The smooth curves represent the theoretically calculated QTL heritability and the noisy curves are the average QTL heritability estimated from 40 replicated simulation experiments.

Correction for the bias

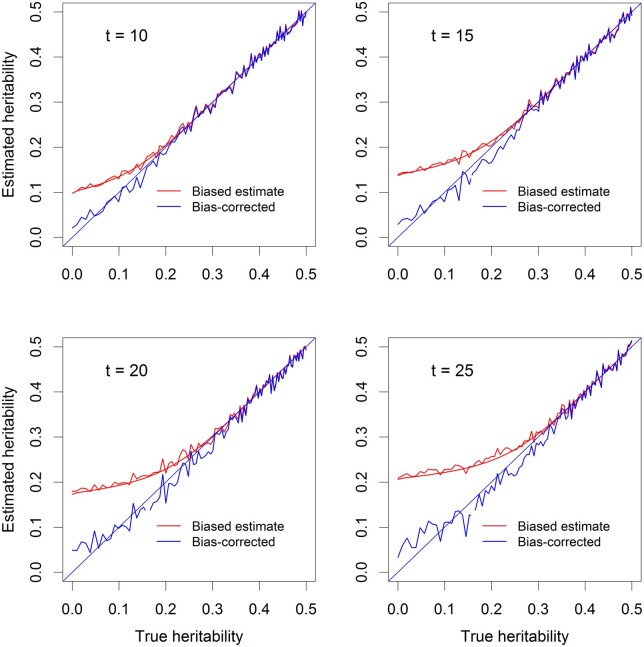
Figure 2 illustrates the bias-corrected heritability for four different levels of the test statistic thresholds ($t_W=10, 15, 20, 25$) when the samples size is $n=100$. The QTL heritability ranges from 0 to 0.5. The red curves show the biased QTL heritability (noisy curves from simulated data and smooth curves are theoretically predicted values) and the blue curves show the bias corrected QTL heritability. We can see that, after correction, the estimated QTL heritability is closer to the true value on the diagonal.

Figure 2.

Correction for the bias of estimated QTL heritability. The simple linear model was used in the simulation (without polygenic background control). There are four levels of the test threshold (t = 10, 15, 20, 25) and the sample size is n = 100. The noisy curves are the average estimated QTL heritability from 40 replicated simulation experiments. The smooth curves are the predicted QTL heritability. The red curves are the QTL heritability prior to the correction for the Beavis effect (deviated from the diagonal). Blue curves are the QTL heritability after correction for the Beavis effect (closer to the diagonal).

Simulation for genome-wide association studies

Genome-wide association studies differ from QTL mapping in the application of mixed models where the fixed effects include population structure and systematic environmental effects and the random effect is represented by a polygenic effect (Yu et al. 2006; Kang et al. 2010; Lippert et al. 2011; Zhou and Stephens 2012). If the pedigree relationships are unknown, the covariance structure of the polygene is often captured by a marker inferred kinship matrix. In this study, we simulated multiple full sib families with a constant family size of five ($m=5$) for all families. For example, if the number of families is $n_f=20$, the total sample size will be $n=m\times n_f=5\times 20=100$. The kinship matrix for n individuals is a block diagonal matrix with $n_f=20$ blocks, where each block is a $5\times 5$ matrix of additive relationship among full-siblings (diagonal elements equal to 1 and off-diagonal elements equal to 0.5). The covariance among families is zero. The sample size varied from $n=100$ to $n=400$ incremented by 100, corresponding to $n_f$ varying from 20 to 80 incremented by 20. The polygenic variance captured by the pedigrees was set at ${\varphi }^2=10$ while the residual variance was set at ${\sigma }^2=10$, resulting in a ratio of $\lambda ={\varphi }^2/{\sigma }^2=10/10=1$. The QTL variance is determined by the QTL heritability by solving for ${\sigma }_{\gamma }^2$ from $h_{\mathit{QTL}}^2={\sigma }_{\gamma }^2/({\sigma }_{\gamma }^2+{\varphi }^2+{\sigma }^2)$, which is

$${\sigma }_{\gamma }^2=({\varphi }^2+{\sigma }^2)h_{\mathit{QTL}}^2/(1-h_{\mathit{QTL}}^2)$$ (64)

The QTL effect takes the square root of the QTL variance,

$$\gamma =\sqrt{{\sigma }_{\gamma }^2}=\sqrt{({\varphi }^2+{\sigma }^2)h_{\mathit{QTL}}^2/(1-h_{\mathit{QTL}}^2)}$$ (65)

The phenotypic value of individual j was generated from the following model,

$$y_j=\mu +Z_j\gamma +{\xi }_j+{\epsilon }_j$$ (66)

where $\mu =100$ is the grand mean, $Z_j$ is a standardized genotype indicator variable for the simulated QTL, ${\xi }_j\sim N(0,{\varphi }^2)$ and $\mathrm{cov}({\xi }_i,{\xi }_j)=K_{ij}{\varphi }^2$, where $K_{ij}=0.5$ if $i$ and $j$ are from the same family and $K_{ij}=0$ otherwise. The QTL heritability varied from 0 to 0.3 incremented by 0.005. Each parameter combination was replicated 40 times. The average estimated QTL heritability was reported and compared with the theoretical value.

Biased QTL heritability

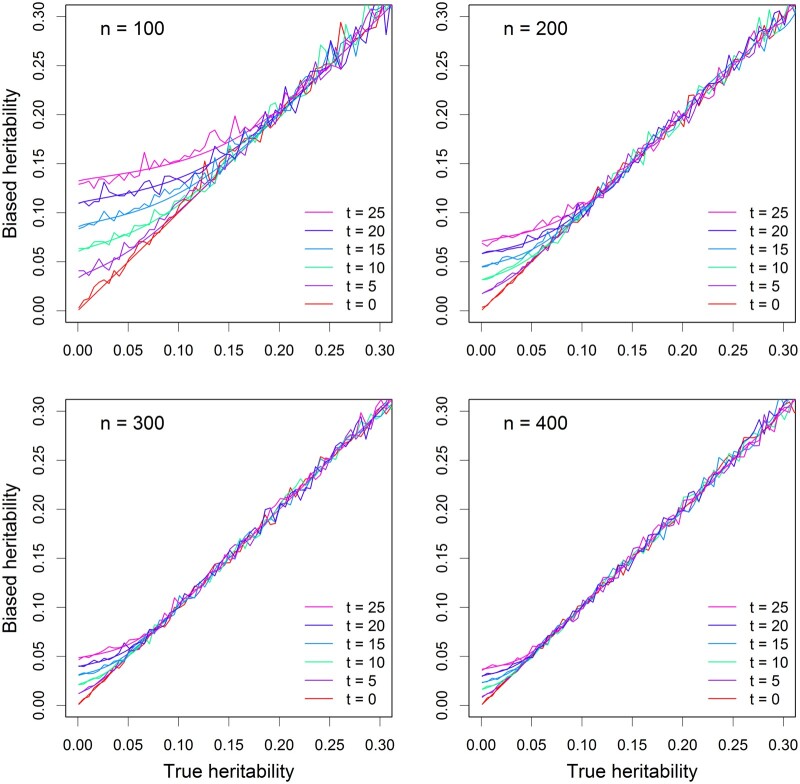
Figure 3 shows the estimated QTL heritability (noisy curves) compared with the theoretically predicted QTL heritability (smooth curves). As the heritability increases, the bias (deviation from the diagonal) becomes smaller (closer to the diagonal). The bias decreases as the sample size (n) increases. The bias also increases as the threshold ($t_W$) increases. The simulation results behave exactly as predicted from the theory. Comparing Figure 3 with Figure 1, we observed less variation among the 40 replicates in the polygenic model than in the simple linear model.

Figure 3.

Comparison of estimated QTL heritability with true QTL heritability from replicated simulation experiments. There are four different sample sizes (n) and six different threshold of the test statistics (t). The linear mixed model (with polygenic background control) was used in the simulation experiments. The smooth curves represent the theoretical QTL heritability and the noisy curves are the average QTL heritability estimated from 40 replicated simulation experiments.

Correction for the bias

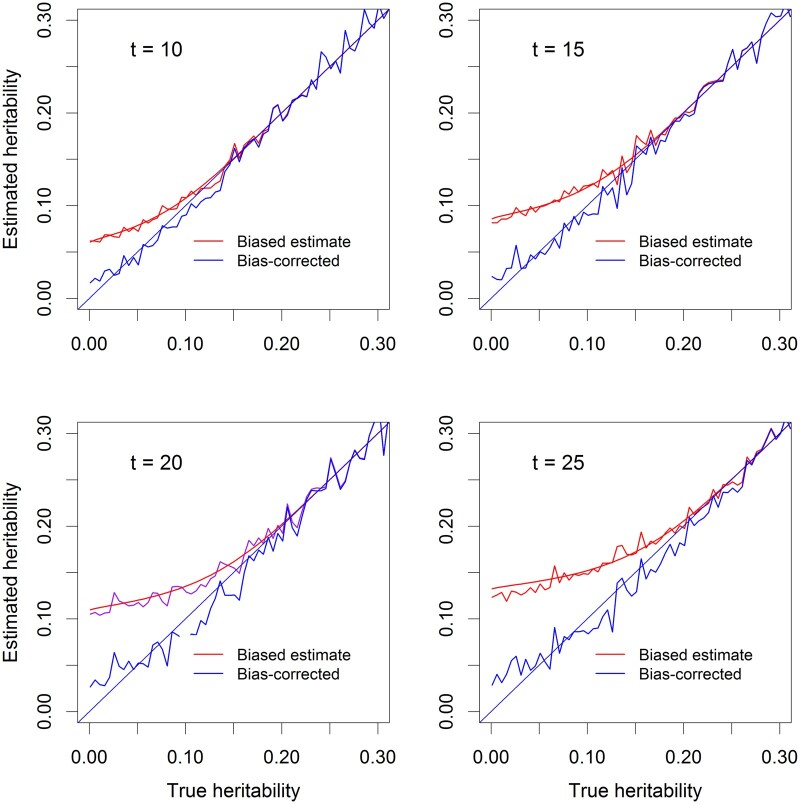
Figure 4 illustrates the bias-corrected QTL heritability for four different levels of the test statistic thresholds ($t_W$) when the samples size is $n=100$. The QTL heritability ranges from 0 to 0.3. The red curves show the biased QTL heritability and the blue curves show the bias corrected QTL heritability. We can see that, after correction, the estimated QTL heritability is closer to the diagonal. This means that we have successfully corrected the bias caused by significance tests under the polygenic model.

Figure 4.

Correction for the bias of estimated QTL heritability. The linear mixed model was used (with polygenic background control). There are four levels of the test threshold (t = 10, 15, 20, 25) and the sample size is n = 100. The noisy curves are the average estimated QTL heritability from 40 replicated simulation experiments. The smooth curves are the predicted QTL heritability. The red curves are the QTL heritability prior to the bias correction (deviated from the diagonal). The blue curves are the QTL heritability after the bias correction (closer to the diagonal).

Bootstrap and conditional maximum likelihood estimators

Three bootstrap estimators have been evaluated in this study. Details of the bootstrap method can be found from previous publications (Sun and Bull 2005; Wu et al. 2005, 2006; Sun et al. 2011; Poirier et al. 2015) and are also described in Appendix B of this study. The conditional maximum likelihood method (Xiao and Boehnke 2009, 2011) has been implemented in a one parameter approach where only sufficient statistics of the original data are analyzed. Details of the conditional maximum likelihood were presented in the original publication (Xiao and Boehnke 2009, 2011) and a slightly modified version is given in Appendix C of this study. The bootstrap and conditional maximum likelihood methods were briefly compared with the moment method developed here. We simply tested the differences between these methods in a simple situation where no polygenic effect was included in the linear model and the sample size was set at $n=100$. The QTL heritability varied at 0.05, 0.10, 0.15, and 0.20. The residual error variance was set at ${\sigma }^2=20$. Under each level of the QTL heritability, the simulation was replicated 100 times and the average estimated QTL heritability over the 100 replicates was reported. The biased or naïve estimate was the estimate from all samples with the Wald test statistic greater than $t_W=10$. The moment estimate was the procedure developed in this study. The conditional maximum likelihood method was originally developed by Xiao and Boehnke (2009, 2011) for a truncated noncentral t distribution and slightly modified to a truncated noncentral Chi-square distribution here (see Appendix C). The three specific bootstrap estimators are the shrinkage estimator, the estimation sample estimator and the weighted estimator. The estimation sample estimate was called the “out of sample” estimator in the original publication (Sun and Bull 2005; Wu et al. 2005, 2006; Sun et al. 2011; Poirier et al. 2015). The number of bootstrap samples was set at $B=1000$. The actual number of bootstrap samples was much higher than 1000 because samples with the W test statistics less than $t_W=10$ were discarded. Table 1 shows the average estimated QTL heritability obtained from 100 replicated simulations. The naïve biased estimates are indeed biased upward compared to the true values (except for high heritability). The moment and conditional maximum likelihood estimates are very similar to each other, but both over corrected the QTL heritability. The three bootstrap estimators vary considerably, some over estimating and some under estimating the QTL heritability. No method is consistently better than all other methods across all situations. We observed that for small effect QTL, the bootstrap estimators under corrected the QTL heritability. For large effect QTL, the bootstrap estimators over corrected the QTL heritability. These observations are consistent with the simulation results of Wu et al. (2005).

Table 1.

Bias corrected QTL heritability from the conditional maximum likelihood method and the bootstrap method

Method	QTL Heritability
	0.05	0.10	0.15	0.20
Biased estimatea	0.1105	0.1357	0.1577	0.1976
Moment estimateb	0.0426	0.0879	0.1232	0.1783
Conditional likelihoodc	0.0399	0.0901	0.1269	0.1831
Shrinkage estimated	0.0386	0.0792	0.1132	0.1659
Estimation sample estimated	0.0765	0.1088	0.1364	0.1825
Weighted estimated	0.0889	0.1187	0.1442	0.1881

^aBiased or naïve estimate after significance test.

^bBias corrected moment estimate (this study).

^cBias corrected conditional likelihood estimate.

^dBias corrected estimate via bootstrapping.

Application of the bias corrected heritability to a rice population

The rice data of Chen et al. (2014) was used as an example to demonstrate the linear mixed model procedure of GWAS and the Beavis effect. The rice population consists of 524 varieties collected from a wide range of geographical locations with a diverse genetic background, including indica, japonica and some intermediate types between the two subspecies. The trait analyzed is the grain width (GW) trait. The number of SNP markers is $m=314393$, covering the 12 chromosomes of the rice genome. The Bonferroni corrected threshold was used as the cut-off point for declaration of statistical significance. Let $F_{{\chi }^2}(x,k)$ be a Chis-square distribution function for argument x with k degrees of freedom. Define $p=1-F_{{\chi }^2}(x,k)$ as the P-value at value x in the Chi-square distribution. The critical value is calculated from

$$t_W=F_{{\chi }^2}^{-1}(1-\alpha /m,k)=F_{{\chi }^2}^{-1}(1-0.05/314393,1)=27.47624$$ (67)

where $\alpha =0.05$ is the nominal Type 1 error, $p=\alpha /m$ is the Bonferroni corrected experiment wise Type 1 error and $k=1$ is the degree of freedom. The corresponding value of the threshold in the Manhattan plot is $-{\hspace{0.17em}\text{log}\hspace{0.17em}}_{10}(0.05/314393)=6.7985$. Figure 5A shows the Manhattan plot, where the red horizontal line is the cut-off point for significance test ($6.7985$). Three regions of the genome have markers with values that exceed the cut-off point. The highest peak appears on chromosome 5, which overlaps with a cloned gene (GW5) that controls the grain-width trait and the grain-length-to-grain-width-ratio trait (Wan et al. 2008). The second peak occurs on chromosome 9 (GW9). Figure 5 also shows the plot of the estimated heritability against genome location before bias correction (Panel B) and after bias correction (Panel C). Obviously, only loci that have passed the critical threshold have nonzero estimated heritability after the bias correction. In practice, only statistically significant loci are to be corrected for their estimated QTL heritability, because the corrected heritability will be zero for all nonsignificant loci.

Figure 5.

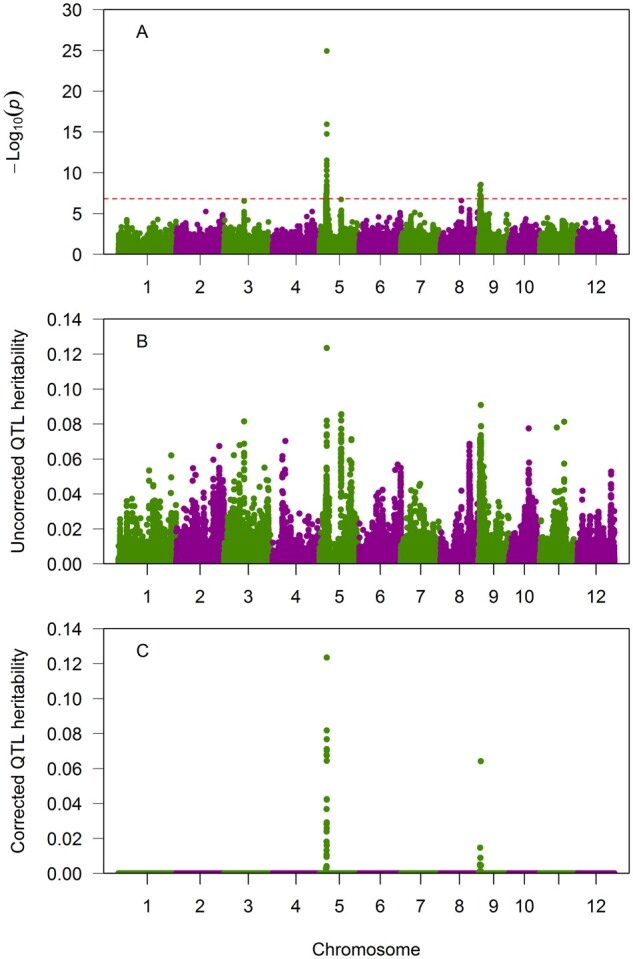
Manhattan plot of the rice genome for GW. (A) Manhattan plot, where the red broken horizontal line indicates the Bonferroni corrected threshold in –Log(p). (B) Plot of the estimated QTL heritability before the Beavis effect correction. (C) Plot of the estimated QTL heritability after the Beavis effect correction.

There are a total of 42 markers whose Wald test statistics passed the threshold value of$t_W=27.47624.$ The greatest peak occurs on chromosome 5 overlapped a cloned gene (GW5) controlling GW. The Wald test is $W=109.5486$ and the corresponding P-value is $p=1.23\times {10}^{-25}$. The peak value in the Manhattan plot corresponding to this P-value is $-\text{log}\hspace{0.17em}10(1.23\times {10}^{-25})=24.91009$. The estimated polygenic variance is ${\widehat{\varphi }}^2=0.130845$, the estimated residual variance is ${\widehat{\sigma }}^2=0.01426$, the estimated variance ratio is $\widehat{\lambda }={\widehat{\varphi }}^2/{\widehat{\sigma }}^2=9.175674$, the estimated marker effect of the peak is $\widehat{\gamma }=-0.14361$, and the standard error of the estimated QTL effect is

$$s_{\widehat{\gamma }}=\sqrt{\mathrm{var}(\widehat{\gamma }|\gamma )}=\sqrt{0.000188}=0.01372$$

The estimated QTL variance from the moment method is

$${\widehat{\sigma }}_{\gamma }^{2(\text{BIASED})}={\widehat{\gamma }}_{}^2-{\widehat{s}}_{\widehat{\gamma }}^2=0.020622-0.000188=0.020434$$

The estimated QTL heritability is

$${\widehat{h}}_{\mathit{QTL}}^{2(\text{BIASED})}=\frac{{\widehat{\sigma }}_{\gamma }^{2(\text{BIASED})}}{{\widehat{\sigma }}_{\gamma }^{2(\text{BIASED})}+{\widehat{\varphi }}^2+{\widehat{\sigma }}^2}=\frac{0.020434}{0.020434+0.130845+0.01426}=0.123441$$

The critical value for the Wald test is $t_W=27.47622$. The bias-corrected QTL variance is obtained by solving the noncentrality parameter ($\delta$) from the following equation,

$$\mathit{E}\left[{\chi }_1^2(\delta )|{\chi }_1^2(\delta )>27.47622\right]=109.5486$$

The solution is $\widehat{\delta }=108.5486$. The bias-corrected QTL variance is

$${\widehat{\sigma }}_{\gamma }^{2(\text{CORRECTED})}=s_{\widehat{\gamma }}^2\widehat{\delta }=0.000188\times 108.5486=0.020434$$

Therefore, the bias corrected QTL heritability is

$${\widehat{h}}_{\mathit{QTL}}^{2(\text{CORRECTED})}=\frac{{\widehat{\sigma }}_{\gamma }^{2(\text{CORRECTED})}}{{\widehat{\sigma }}_{\gamma }^{2(\text{CORRECTED})}+{\widehat{\varphi }}^2+{\widehat{\sigma }}^2}=\frac{0.020434}{0.020434+0.130845+0.01426}=0.123441$$

This bias-corrected heritability is the same as the original uncorrected QTL heritability because both the QTL size and the sample size are sufficiently large and the Beavis effect has played no role in the estimated QTL heritability.

The second highest peak appears on chromosome 9 with an estimated QTL heritability of 0.09087. After correction for the Beavis effect, the heritability becomes 0.064233, which is $(0.09087-0.064233)/0.09087=29.316345\%$ lower than the biased heritability prior to the Beavis correction. Compared with the first peak on chromosome 5, correction for the Beavis effect of the second peak has significantly reduced the QTL heritability. The estimated genetic parameters for the two loci at the peaks are summarized in Table 2.

Table 2.

Summary of estimated genetic parameters for the two peak loci of the rice genome

Parameter	QTL1 (GW5)	QTL2 (GW9)
Estimated QTL effect ($\widehat{\gamma }$)	−0.1436	−0.1340
Standard error ($s_{\widehat{\gamma }}^{}$)	0.0137	0.0226
Wald test	109.5486	35.2473
P-value	1.23E-25	2.90E-09
QTL variance before correction (${\widehat{\sigma }}_{\mathit{QTL}}^{2(\text{BIASED})}$)	0.0204	0.0175
QTL variance after correction (${\widehat{\sigma }}_{\mathit{QTL}}^{2(\text{CORRECTED})}$)	0.0204	0.0120
Estimated polygenic variance (${\widehat{\varphi }}^2$)	0.1308	0.1604
Estimated residual variance (${\widehat{\sigma }}^2$)	0.0143	0.0142
QTL heritability before correction (${\widehat{h}}_{\mathit{QTL}}^{2(\text{BIASED})}$)	0.1234	0.0909
QTL heritability after correction (${\widehat{h}}_{\mathit{QTL}}^{2(\text{CORRECTED})}$)	0.1234	0.0642
Effective sample size $(n_0)$	218.2185	198.8164

The heritability of the two loci were also estimated via the conditional maximum likelihood method (Sun and Bull 2005; Sun et al. 2011). The bias corrected estimates of the heritability for the two loci are 0.1245 and 0.0663, respectively. These estimates are very close to the bias corrected estimates from the moment method (see Table 2). The bootstrap method failed to generate bias corrected estimates of the QTL heritability for the two loci because the kinship matrices for the bootstrap samples are not positive definite.

Discussion

The ultimate benefit of reporting bias-corrected QTL sizes is to provide an accurate understanding of a quantitative trait, avoiding over optimistic expectation of the potential benefit from detected QTL. Therefore, we recommend all QTL mapping studies to include the bias-corrected QTL sizes. Adjusting for the Beavis effect requires estimated QTL effects, the standard errors of the estimates and the Wald test statistics of all detected loci. Most QTL mapping and GWAS software packages allow users to report the estimated QTL effect and the test statistic for each locus. We have enough information to perform the bias correction, because the standard error of the estimated QTL effect can be found from the two pieces of information. If the test statistic is the t-test, $t=\left|\widehat{\gamma }\right|/s_{\widehat{\gamma }}^{}$, the standard error can be recovered from $s_{\widehat{\gamma }}^{}=\left|\widehat{\gamma }\right|/t$. The Wald test statistic is defined as $W={\widehat{\gamma }}^2/s_{\widehat{\gamma }}^2$ and thus the square of the standard error is recovered from $s_{\widehat{\gamma }}^2={\widehat{\gamma }}^2/W$. The outputs of most QTL mapping software packages include both the estimated effects and the standard errors. Given the threshold ($t_W$), define $\delta ={\sigma }_{\gamma }^2{s}_{\widehat{\gamma }}^2$ as the noncentrality parameter, the bias-corrected QTL variance is obtained via

$$\mathit{E}\left[{\chi }_1^2(\delta )|{\chi }_1^2(\delta )>t_W\right]=W$$

The solution for $\delta$ is obtained iteratively. Let $\widehat{\delta }$ be the solution, the bias-corrected QTL variance is ${\widehat{\sigma }}_{\gamma }^{2(\text{CORRECTED})}=s_{\widehat{\gamma }}^2\widehat{\delta }$. If the sample size is not too small, say $n>30$, we can convert the t-test into the corresponding Wald test via $W=t^2$, where this t is the t-test statistic, not the threshold $t_W$ in W. If the output of a software package reports the LOD score rather than the Wald test for a significant locus, the corresponding Wald test can be achieved via $W=4.61 \text{LOD}$. The threshold in W should also be converted this way accordingly, i.e., $t_W=4.61 t_{\mathit{LOD}}$. If the threshold is in the P-value after Bonferroni correction, we can convert the P-value threshold (say $p_W={10}^{-7}$) into the threshold in the Wald test using

$$t_W=F_{{\chi }^2}^{-1}(1-p_W,1)=F_{{\chi }^2}^{-1}(1-{10}^{-7},1)=28.3740$$

If the output of a QTL mapping software package does not include the Wald test, but the P-value (denoted by p), the conversion formula is

$$W=F_{{\chi }^2}^{-1}(1-p,1)$$

A recommendation to software developers is to report the Wald test statistic (W), the estimated QTL effect ($\widehat{\gamma }$) and the standard error of the estimated QTL effect ($s_{\widehat{\gamma }}^{}$) for each locus, where $\widehat{\gamma }$ and $s_{\widehat{\gamma }}^{}$ are needed for meta-analyses using the inverse variance weighted method (Kang et al. 2014).

Theory and methods of the Beavis effect were derived based on a standardized genotype indicator variable Z for convenience of presentation. We recommend that QTL and GWAS software developers standardize the Z variables prior to the data analysis, although existing software packages may not have done so. The easiest way to fix this issue is to modify the estimated QTL effect and the standard error. Recall that the linear mixed model (43) for GWAS contains the QTL item with $Z\gamma$, where Z has been standardized, i.e., ${\sigma }_Z^2=1$. Let $Z^{*}$ be the Z variable in the original scale and ${\gamma }^{*}$ be the QTL effect in the original scale, where ${\sigma }_{Z^{*}}^2\ne 1$. The relationship between $\gamma$ and ${\gamma }^{*}$ is

$${\sigma }_{\mathit{QTL}}^2=\mathrm{var}(Z\gamma )=\mathrm{var}(Z^{*}{\gamma }^{*})$$

where $\mathrm{var}(Z\gamma )={\sigma }_Z^2{\gamma }^2={\gamma }^2$ and $\mathrm{var}(Z^{*}{\gamma }^{*})=\mathrm{var}(Z^{*}){\gamma }^{*2}={\sigma }_{Z^{*}}^2{\gamma }^{*2}$. Therefore,

$$\widehat{\gamma }={\sigma }_{Z^{*}}{\widehat{\gamma }}^{*}$$

The squared error of $\widehat{\gamma }$ is

$$s_{\widehat{\gamma }}^2=\mathrm{var}(\widehat{\gamma }|\gamma )=\mathrm{var}({\sigma }_{Z^{*}}{\widehat{\gamma }}^{*}|{\gamma }^{*})={\sigma }_{Z^{*}}^2\mathrm{var}({\widehat{\gamma }}^{*}|{\gamma }^{*})={\sigma }_{Z^{*}}^2{s}_{{\widehat{\gamma }}^{*}}^2$$

The Wald test statistic remains the same, regardless of the scale in the Z variable. With the modified $\widehat{\gamma }$ and $s_{\widehat{\gamma }}^2$, correction can be proceeded as we do for standardized Z variables.

Correction for the Beavis effect and theoretical evaluation of the potential impact of the Beavis effect are separate issues. Understanding the Beavis effect can help us develop an optimal design of experiment for a follow-up QTL mapping study. In the experimental design stage, one needs to consider the sample size required to detect a QTL with a predetermined power. A sample size sufficient for detecting the QTL may not be enough to guarantee that the QTL heritability will not be overly estimated.

Most QTL mapping and GWAS tools are designed for detecting additive effects because additive effects are considered to be more important than nonadditive effects, especially in breeding programs that focus on developing conventional pure bred cultivars. However, detection of dominance and epistatic effects may also be interesting for some investigators. The procedure developed in this study only concerns the additive effects. Extension to dominance effects is straightforward but incorporation of both the additive and dominance effects requires more complicated models, which deserves further studies.

Another extension of the Beavis effect is bias correction for meta-analysis. Meta-analysis is to combine results from multiple studies of the same locus for the same trait and report a consensus result (Kang et al. 2014). Since the reported QTL effects and the standard errors from the multiple studies are all truncated with $W>t_W$, the consensus estimated QTL effect is biased and thus correction is needed.

In classical quantitative genetics, there is another effect associated with selection, which is called the Bulmer effect (Bulmer 1976). The Bulmer effect is a downward bias in genetic variance after selection. So, the Beavis effect is the upward bias in expectation and the Bulmer effect is the downward bias in variance, both due to selection.

Data availability

Data and program code are provided in six Supplementary Folders, which are described as follows.

Supplementary Folder 1: This folder contains “mixed725.SAS,” a SAS code for PROC MIXED, “kinship725.xlsx” is a 278 × 278 marker inferred kinship matrix, “phegen725.xlsx” contains the phenotypic values of rice 1000-grain-weight (KGW) trait from 278 rice genotypes along the numerical code (z0) of the 725th bin (marker) and the standardized genotypic code (z).

Supplementary Folder 2: The folder contains “mixedFunction.R” (mixed() function in R to perform mixed model analysis) and “mixed.R” (R code to read the sample data and to call the mixed() function for data analysis). The two rice data in Folder 1 are also stored in this folder.

Supplementary Folder 3: This folder contains three files: “beavis.R” is an R function to correct the Beavis effect, “kinship725.csv” and “kinship725.xlsx” is a kinship matrix stored in two different file types.

Supplementary Folder 4: This folder stores the 524 rice variety data, including “gen524.RData” for genotypes of 314393 SNPs, “kk524.RData” for a 524 × 524 kinship matrix calculated from markers of the whole genome, “phe524.csv” for the phenotypic values of five traits, “Output-marker135000-marker136000.csv” for the GWAS output with corrected QTL heritability of all markers between 135000 and 136000, “mixedFunction.R” for the R function of the mixed model analysis, and “mixed.R” for the R code to read the data and call the mixed() function.

Supplementary Folder 5: This folder contains two R programs to simulate the data for validating the bias and correcting the bias for the Winners’ curse in QTL mapping, where “simulIntervalValidation.R” is to validate the bias and “simulIntervalCorrection.R” is to correct the bias.

Supplementary Folder 6: This folder contains two R programs to simulate the data for validating the bias and correcting the bias for the Winners’ curse in GWAS, where “simulPolygeneValidation.R” is to validate the bias and “simulPolygenCorrection.R” is to correct the bias.

Supplementary material is available at GENETICS online.

Appendix A: The effective sample size (n₀)

The variance-covariance matrix of the BLUE of fixed effects is

$$\mathrm{var}\left[\begin{array}{c}\widehat{\mathbf{\beta }}\\ \widehat{\mathbf{\gamma }}\end{array}\right]={\left[\begin{array}{cc}{\mathbf{X}}^T{\mathbf{H}}^{-1}\mathbf{X}& {\mathbf{X}}^T{\mathbf{H}}^{-1}{\mathbf{Z}}_{}\\ {\mathbf{Z}}_{}^T{\mathbf{H}}^{-1}\mathbf{X}& {\mathbf{Z}}_{}^T{\mathbf{H}}^{-1}{\mathbf{Z}}_{}\end{array}\right]}^{-1}{\widehat{\sigma }}^2=\left[\begin{array}{cc}{\mathbf{C}}_{XX}& {\mathbf{C}}_{XZ}\\ {\mathbf{C}}_{ZX}& {\mathbf{C}}_{ZZ}\end{array}\right]{\widehat{\sigma }}^2$$ (A1)

where

$${\mathbf{C}}_{ZZ}={({\mathbf{Z}}^T\mathbf{P}\mathbf{Z})}^{-1}$$

and

$$\mathbf{P}={\mathbf{H}}^{-1}-{\mathbf{H}}^{-1}\mathbf{X}{({\mathbf{X}}^T{\mathbf{H}}^{-1}\mathbf{X})}^{-1}{\mathbf{X}}^T{\mathbf{H}}^{-1}$$

The variance of the estimated QTL effect (squared estimation error) is

$$\mathrm{var}(\widehat{\gamma }|\gamma )=s_{\widehat{\gamma }}^2={\mathbf{C}}_{ZZ}{\widehat{\sigma }}^2=\frac{{\widehat{\sigma }}^2}{{\mathbf{Z}}^T\mathbf{P}\mathbf{Z}}=\frac{{\widehat{\sigma }}^2}{n_Z}$$ (A2)

where $n_Z={\mathbf{Z}}^T\mathbf{P}\mathbf{Z}$, which is an observed data point depending on Z. The theoretical value of the variance (squared error) is

$$s_{\gamma }^2=\frac{{\sigma }^2}{\mathit{E}({\mathbf{Z}}^T\mathbf{P}\mathbf{Z})}=\frac{{\sigma }^2}{\mathit{tr}(\mathbf{P})}=\frac{{\sigma }^2}{n_0}$$ (A3)

where

$$n_0\mathit{=E}({\mathbf{Z}}^T\mathbf{P}\mathbf{Z})=\mathit{E}({\mathbf{Z}}^T)\mathbf{P}\mathit{E}(\mathbf{Z})+\mathit{tr}\left[\mathrm{var}(\mathbf{Z})\mathbf{P}\right]=\text{tr}(\mathbf{P})$$ (A4)

is the effective sample size. Note that $\mathrm{E}(\mathbf{Z})=0$ and $\mathrm{var}(\mathbf{Z})=\mathbf{I}$ because Z has been standardized prior to the data analysis. We now prove ${\mathbf{C}}_{ZZ}={({\mathbf{Z}}^T\mathbf{P}\mathbf{Z})}^{-1}$. The proof requires the inverse of a blocked (partitioned) matrix,

$${\left[\begin{array}{cc}\mathbf{A}& \mathbf{B}\\ {\mathbf{B}}^T& \mathbf{D}\end{array}\right]}^{-1}=\left[\begin{array}{cc}{\mathbf{A}}^{-1}+{\mathbf{A}}^{-1}\mathbf{B}{(\mathbf{D}-{\mathbf{B}}^T{\mathbf{A}}^{-1}\mathbf{B})}^{-1}{\mathbf{B}}^T{\mathbf{A}}^{-1}& -{\mathbf{A}}^{-1}\mathbf{B}{(\mathbf{D}-{\mathbf{B}}^T{\mathbf{A}}^{-1}\mathbf{B})}^{-1}\\ -{(\mathbf{D}-{\mathbf{B}}^T{\mathbf{A}}^{-1}\mathbf{B})}^{-1}{\mathbf{B}}^T{\mathbf{A}}^{-1}& {(\mathbf{D}-{\mathbf{B}}^T{\mathbf{A}}^{-1}\mathbf{B})}^{-1}\end{array}\right]$$ (A5)

The inverse of the blocked matrix in the BLUE is

$${\left[\begin{array}{cc}{\mathbf{X}}^T{\mathbf{H}}^{-1}\mathbf{X}& {\mathbf{X}}^T{\mathbf{H}}^{-1}{\mathbf{Z}}_{}\\ {\mathbf{Z}}_{}^T{\mathbf{H}}^{-1}\mathbf{X}& {\mathbf{Z}}_{}^T{\mathbf{H}}^{-1}{\mathbf{Z}}_{}\end{array}\right]}^{-1}={\left[\begin{array}{cc}\mathbf{A}& \mathbf{B}\\ {\mathbf{B}}^T& \mathbf{D}\end{array}\right]}^{-1}$$ (A6)

Therefore, $\mathbf{A}={\mathbf{X}}^T{\mathbf{H}}^{-1}\mathbf{X}$, $\mathbf{B}={\mathbf{X}}^T{\mathbf{H}}^{-1}\mathbf{Z}$, ${\mathbf{B}}^T={\mathbf{Z}}^T{\mathbf{H}}^{-1}\mathbf{X}$ and $\mathbf{D}={\mathbf{Z}}^T{\mathbf{H}}^{-1}\mathbf{Z}$. As a result,

$$\begin{array}{c}{\mathbf{C}}_{ZZ}={(\mathbf{D}-{\mathbf{B}}^T{\mathbf{A}}^{-1}\mathbf{B})}^{-1}\\ ={\left[{\mathbf{Z}}^T{\mathbf{H}}^{-1}\mathbf{Z}-{\mathbf{Z}}^T{\mathbf{H}}^{-1}\mathbf{X}{({\mathbf{X}}^T{\mathbf{H}}^{-1}\mathbf{X})}^{-1}{\mathbf{X}}^T{\mathbf{H}}^{-1}\mathbf{Z}\right]}^{-1}\\ ={\left\{{\mathbf{Z}}^T\left[{\mathbf{H}}^{-1}-{\mathbf{H}}^{-1}\mathbf{X}{({\mathbf{X}}^T{\mathbf{H}}^{-1}\mathbf{X})}^{-1}{\mathbf{X}}^T{\mathbf{H}}^{-1}\right]\mathbf{Z}\right\}}^{-1}\\ ={({\mathbf{Z}}^T\mathbf{P}\mathbf{Z})}^{-1}\end{array}$$ (A7)

which concludes the proof.

Appendix B: The Bootstrap method

The bootstrap method for correcting the bias in estimated QTL variance consist of three specific estimators (Sun and Bull 2005; Sun et al. 2011). Let ${\widehat{h}}_N^2$ be the naïve estimate of the QTL heritability from the original sample. Let B be the number of bootstrap samples in which the test statistics are significant. Depending on the sample size and the magnitude of the QTL heritability, the actual number of bootstrap samples can be substantially larger than B because all samples with the test statistics less than the threshold ($t_W$) are discarded. In other words, the B bootstrap samples are censored. A sample is included in the bootstrap samples only if its test statistic has passed the critical value of the test statistic. Let $h_D^{2(b)}$ be the estimated QTL heritability from the bth bootstrap sample for $b=1,2,\dots ,B$. Let $h_E^{2(b)}$ be the estimated QTL heritability from the bth estimation sample. An estimation sample is a sample excluding all individuals that appear in a bootstrap sample. A bootstrap sample is also called a detection sample. The QTL heritability obtained from the estimation sample is

$${\widehat{h}}_O^2=\frac{1}{B}\sum _{b=1}^B{h}_E^{2(b)}$$ (B1)

Another estimate from the bootstrap samples is called the shrinkage estimate, which is defined as

$${\widehat{h}}_S^2={\widehat{h}}_N^2-({\widehat{h}}_D^2-{\widehat{h}}_O^2)={\widehat{h}}_N^2-{\widehat{h}}_D^2+{\widehat{h}}_O^2$$ (B2)

where

$${\widehat{h}}_D^2=\frac{1}{B}\sum _{b=1}^B{h}_D^{2(b)}$$ (B3)

Combining the naïve estimate and the estimate from the estimation sample leads to a third estimate of the QTL heritability, called the weighted estimate,

$${\widehat{h}}_W^2=0.368{\widehat{h}}_N^2+0.632{\widehat{h}}_O^2$$ (B4)

Regarding the definition of an estimation sample, it is a sample for all individuals in the original sample that are not included in the corresponding bootstrap (detection) sample. Let $n=10$ be the original sample size with 10 observations, say 1, 2, 3, $\cdots$, 10. A bootstrap sample contains exactly 10 observations but they are sampled with replacement. For example, a bootstrap sample may include observations 2, 3, 3, 5, 6, 10, 2, 3, 1. The corresponding estimation sample includes observations 4, 7, 8, 9, which do not appear in the bootstrap sample. In summary, there are three bootstrap estimators, the estimate from the estimation sample (${\widehat{h}}_O^2$), the shrinkage estimate (${\widehat{h}}_S^2$) and the weighted estimate $({\widehat{h}}_W^2)$.

Appendix C: The conditional maximum likelihood method

The conditional maximum likelihood methods for correcting the bias in an estimated QTL variance was developed by Xiao and Boehnke (2009, 2011). They proposed two ascertainment corrected estimates of QTL heritability, a three-parameter approach and a one-parameter approach. The three-parameter approach requires analysis of the original data. It is computationally intensive and thus is not discussed in this study. The one-parameter approach is comparable to the moment method and thus is examined here. Similar to the moment method investigated in this study, Xiao and Boehnke (2009, 2011) used the sufficient statistics, $\widehat{\gamma }$ and $s_{\widehat{\gamma }}^2$, as the “row data” to build the conditional likelihood function. The test statistic is the t-test,

$$t=\frac{\left|\widehat{\gamma }\right|}{s_{\widehat{\gamma }}^{}}$$ (C1)

which follows a noncentral t distribution with $n-2$ degrees of freedom and a noncentrality parameter $\delta =|\gamma |/s_{\widehat{\gamma }}$. Xiao and Boehnke (2011) claimed that $\widehat{\gamma }\sim N(\gamma ,s_{\widehat{\gamma }}^2)$ asymptotically for a typical GWAS sample size ($n>100$), where $\gamma$ is the true QTL effect. The normal density of $\widehat{\gamma }$ is

$$f(\widehat{\gamma }|\gamma ,s_{\widehat{\gamma }}^2)=\frac{1}{\sqrt{2\pi s_{\widehat{\gamma }}^2}}\text{exp}\hspace{0.17em}\left[-\frac{1}{2s_{\widehat{\gamma }}^2}{(\widehat{\gamma }-\gamma )}^2\right]$$ (C2)

Let $t_{1-\alpha /2,n-2}$ be the $1-\alpha /2$ percentile of the central t-distribution where $\alpha$ is the genome-wide Type 1 error rate. The conditional likelihood function is

$$L(\gamma |t>t_{1-\alpha /2,n-2})=\frac{1\left\{t>t_{1-\alpha /2,n-2}\right\}f(\widehat{\gamma }|\gamma ,{\widehat{s}}_{\widehat{\gamma }}^2)}{\mathrm{Pr}(t>t_{1-\alpha /2,n-2})}$$ (C3)

where $\mathrm{Pr}(t>t_{1-\alpha /2,n-2})$ is the probability of the noncentral t variable being greater than the $t_{1-\alpha /2,n-2}$ threshold (statistical power) and the noncentral $t$ has $n-2$ degrees of freedom and a noncentrality parameter of $\delta =|\gamma |/s_{\widehat{\gamma }}$. In the above conditional likelihood function, everything is assumed to be known except $\gamma$ being the unknown parameter. The conditional maximum likelihood estimate of the QTL effect is the $\gamma$ that maximizes the above conditional likelihood function and is denoted by ${\widehat{\gamma }}^{(\text{CORRECTED})}$. The ascertainment-corrected estimate of the QTL heritability is

$${\widehat{h}}_{\mathit{CML}}^{2(\text{CORRECTED})}=\frac{{({\widehat{\gamma }}_{}^{2\left(\text{CORRECTED}\right)}-s_{\widehat{\gamma }}^2)}^{+}}{{({\widehat{\gamma }}_{}^{2\left(\text{CORRECTED}\right)}-s_{\widehat{\gamma }}^2)}^{+}+{\widehat{\sigma }}^2}$$ (C4)

Since $s_{\widehat{\gamma }}^2$ is an estimated variance, not the theoretical variance $s_{\gamma }^2$, standardization of $\widehat{\gamma }$ leads to $t=(\widehat{\gamma }-\gamma )/s_{\widehat{\gamma }}$, which follows a noncentral t distribution. Therefore, the conditional likelihood function is the density of a truncated noncentral t distribution. As a result, the above conditional likelihood function in Equation (C3) is simply the density of a truncated noncentral t distribution

$$L(\gamma |t>t_{1-\alpha /2,n-2})=\frac{1\left\{t>t_{1-\alpha /2,n-2}\right\}f(t|n-2,\delta )}{\mathrm{Pr}(t>t_{1-\alpha /2,n-2})}$$ (C5)

where $\delta =|\gamma |/s_{\widehat{\gamma }}$. Maximizing Equation (C5), the above truncated noncentral t distribution, will produce the maximum likelihood estimate of the QTL effect.

The two-tailed t-test is equivalent to the one-tailed F-test, we can replace the t-test by the F-test with a numerator degree of freedom of 1 and a denominator degree of freedom of $n-2$. Since the typical sample sizes of QTL mapping and GWAS are larger than 100, the F-test can be well approximated by the Wald test (Chi-square test) with 1 degree of freedom. In other words, $t^2=F\approx W$. Since the Wald test follows a noncentral Chi-square distribution, after significance test, the Wald test will follow a truncated noncentral Chi-square distribution with 1 degree of freedom and a noncentrality parameter

$$\delta ={({\gamma }^2-s_{\widehat{\gamma }}^2)}^{+}/s_{\widehat{\gamma }}^2$$ (C6)

Let us define

$$L(\gamma )=f_{{\chi }^2}(W|1,\delta |W>t_W)$$ (C7)

as the probability density of a truncated noncentral Chi-square distribution. We now treat Equation (C7) as the conditional likelihood function. The parameter ($\gamma$) that maximizes $L(\gamma )$ in Equation (C7) is the conditional maximum likelihood estimate of $\gamma$, denoted by ${\widehat{\gamma }}^{(\text{CORRECTED})}$. Let

$${\widehat{\sigma }}_{\gamma }^{2(\text{CORRECTED})}={({\widehat{\gamma }}_{}^{2(\text{CORRECTED})}-s_{\widehat{\gamma }}^2)}^{+}$$ (C8)

be the bias corrected estimate of the QTL variance. The bias corrected estimate of the QTL heritability is

$${\widehat{h}}_{\mathit{CML}}^{2(\text{CORRECTED})}=\frac{{({\widehat{\gamma }}_{}^{2\left(\text{CORRECTED}\right)}-s_{\widehat{\gamma }}^2)}^{+}}{{({\widehat{\gamma }}_{}^{2\left(\text{CORRECTED}\right)}-s_{\widehat{\gamma }}^2)}^{+}+{\widehat{\sigma }}^2}$$ (C9)

This conditional maximum likelihood estimate can be compared with the moment estimate of the QTL heritability.