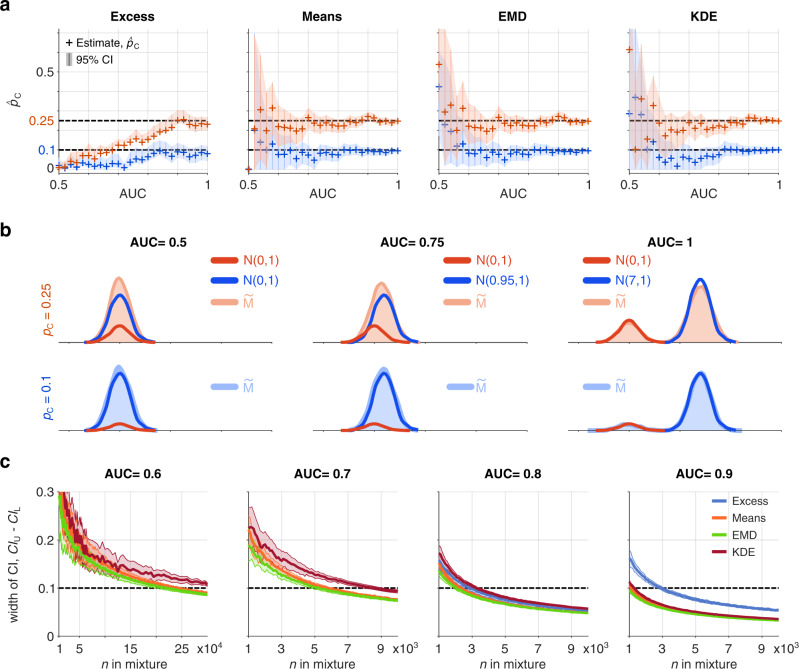
Fig. 4. A comparison of the four methods using an artificial genetic risk score with increasing discriminative ability as measured by AUC, from AUC = 0.5 (no discriminative ability) through to AUC = 1, (complete differentiation).

a The estimated proportion (+ marker) with confidence intervals (vertical lines with shading) around $p_{\mathrm{C}}=0.1$ (blue) or $p_{\mathrm{C}}=0.25$ (red) for each of the methods (Excess, Means, EMD, KDE) are shown using mixture size, $n=5,000$. b The constructed mixture distributions and reference distributions (${\mathrm{R}}_{\mathrm{C}}$, shaded red and ${\mathrm{R}}_{\mathrm{N}}$, shaded blue) from which they were constructed for AUC = {0.5, 0.75, 1}. c Dependence of the width of CI ($C{I}_{\mathrm{U}}-C{I}_{\mathrm{L}}$) on the number of points in the mixture sample for AUC = {0.6, 0.7, 0.8, 0.9} and $p_{\mathrm{C}}=0.1$. Curves and shading show median ± standard deviation of the width of CI. The plot for the Excess method for AUC = {0.6, 0.7} is omitted because the method does not converge to $p_{\mathrm{C}}=0.1$. This figure is generated using artificial data: N(μ,σ) is a normal distribution with mean μ = {0.0, 0.08, 0.15, 0.22, 0.29, 0.37, 0.44, 0.51, 0.59, 0.66, 0.74, 0.82, 0.91, 0.99, 1.09, 1.19, 1.29, 1.4, 1.52, 1.65, 1.81. 1.98, 2.19, 2.47, 2.91, 7} and standard deviation σ = 1 and $\tilde{\mathrm{M}}$ is a mixture of the two normal distributions (${\mathrm{R}}_{\mathrm{C}}$ is always N(0,1)). Both reference samples have $n=2,000$. For AUC=0.5, means of the constructed mixture samples (for $p_{\mathrm{C}}=0.1$ and $p_{\mathrm{C}}=0.25$) were smaller than both means of the reference samples, in these cases the prevalence estimate from the Means method is assumed to be ${\widehat{p}}_{\mathrm{C}}=0$ and confidence intervals are undefined due to undetermined acceleration value.