Table 1.

Analytical Methods for Dealing With Selection Bias Due to Selective Attrition by Death and Study Nonparticipation^a

Method	Causal Estimand	Interpretation	Assumptions b
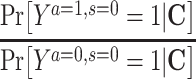
Multivariable adjustmentc		Risk of Y that would have been observed if everyone had been exposed to A and everyone had remained in the study divided by risk of Y if no one had been exposed to A and everyone had remained in the study conditional on C	No unmeasured common cause for an A-Y relationship (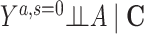) No unmeasured common cause for an S-Y relationship (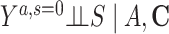) No model misspecification for the outcome (Y) model conditional on A and C
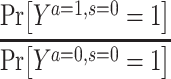
IPTW and IPCWc		Risk of Y that would have been observed if everyone had been exposed to A and everyone had remained in the study divided by risk of Y if no one had been exposed to A and everyone had remained in the study among the study population	No unmeasured common cause for an A-Y relationship (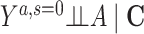) No unmeasured common cause for an S-Y relationship (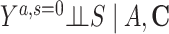) No model misspecification for the exposure (A) model conditional on C No model misspecification for death and attrition (S) conditional on A and C
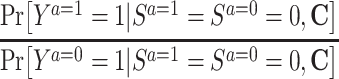
SACEd,e		Risk of Y that would have been observed if everyone had been exposed to A divided by risk of Y if no one had been exposed to A conditional on C in a study population subset of persons who would have remained in the study regardless of the exposure level	No unmeasured common cause for an A-Y relationship (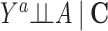) Cross-world exchangeability for an S-Y relationship (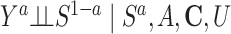) Linear association between U and Y conditional on A and C on the log scalef Linear association between U and S conditional on A and C on the logit scaleg No model misspecification for death and attrition (S) conditional on A and C A does not influence U conditional on Ch Location shift relationship between U and (A, C) given S = 0i

Abbreviations: IPCW, inverse probability of censoring weighting; IPTW, inverse probability of treatment weighting; SACE, survivor average causal effect.

^a  Y is a binary outcome, A is a binary exposure, S = 0 indicates that the person remained in the study (i.e., no censoring), C is a vector of covariates, U is an unmeasured common cause of an outcome and censoring, 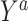is a potential outcome under exposure A = a, and 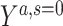is a potential outcome under exposure A = a and S = 0.

^b All approaches also assumed consistency and positivity.

^c Multivariable adjustment and inverse probability weights were based on conditional exchangeability, implied by the directed acyclic graph in Figure 2B.

^d Approach proposed by Tchetgen Tchetgen et al. (37). Assumptions for unmeasured confounder(s) U and model specification are also shown in the original article.

^e The SACE approach was based on conditional exchangeability, implied by the directed acyclic graph in Figure 2C.

^f The log-linear model for the outcome Y conditional on A, U, and C fitted to those who remained in the study (S = 0) was specified as follows: 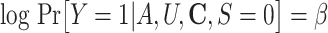, where 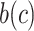is a flexible function of C.

^g The logistic model for the censoring S conditional on A, U, and C was specified as follows: 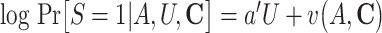, where .

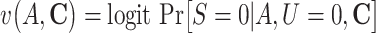^h Formally, this assumption is written as .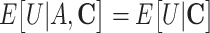

ⁱ Formally, the assumption states that the residual for U (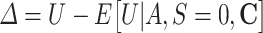) is independent of A and C given S = 0.