Abstract
COVID-19 has affected every individual physically or physiologically, leading to substantial impacts on how they perceive and respond to the pandemic’s danger. Due to the lack of vaccines or effective medicines to cure the infection, an urgent control measure is required to prevent the continued spread of COVID-19. This can be achieved using advanced computing, such as artificial intelligence (AI), machine learning (ML), deep learning (DL), cloud computing, and edge computing. To control the exponential spread of the novel virus, it is crucial for countries to contain and mitigate interventions. To prevent exponential growth, several control measures have been applied in the Kingdom of Saudi Arabia to mitigate the COVID-19 epidemic. As the pandemic has been spreading globally for more than a year, an ample amount of data is available for researchers to predict and forecast the effect of the pandemic in the near future. This article interprets the effects of COVID-19 using the Susceptible-Infected-Recovered (SIR-F) while F-stands for ‘Fatal with confirmation,’ age-structured SEIR (Susceptible Exposed Infectious Removed) and machine learning for smart health care and the well-being of citizens of Saudi Arabia. Additionally, it examines the different control measure scenarios produced by the modified SEIR model. The evolution of the simulation results shows that the interventions are vital to flatten the virus spread curve, which can delay the peak and decrease the fatality rate.
Keywords: COVID-19, Control measurements, Interventions, Mathematical SIR, SIR-F, SEIR, Critical cases
Introduction
In past decades, numerous diseases have emerged in different geographical regions in the world, such as Ebola, Zika virus, Nipah virus, and coronavirus [1]. In December 2019, a novel coronavirus (COVID-19) emerged from the Coronaviridae family in Wuhan, China [2–4].
However, COVID-19 is of zoonotic origin, but it spread via human-to human transmission, and there has been a steady increase in the number of confirmed cases globally. It is clear that the infection transmission rate of this virus is higher than that of other viruses.
Recent studies suggest that COVID-19 is first transmitted from animals, such as bats, to humans. It was previously reported that a group of patients who tested positive for COVID-19 were associated with the seafood market in Wuhan, South China. Later, the virus quickly spread throughout the country and then subsequently to other countries. COVID-19 poses a significant threat to public health.
Looking at the severity of the breakout and the potential of its spread globally, the WHO declared a global health emergency in early January 2020; later, in the month of March 2020, it was declared a pandemic.
COVID-19 in the Kingdom of Saudi Arabia
Coronavirus has been associated with significant disease outbreaks in East Asia and the Middle East in the past 2 decades. Middle East Respiratory Syndrome coronavirus (MERS-CoV) was first reported in Saudi Arabia in September 2012 [5]. The mortality rate of MERS was approximately 37.1%, and many patients experience mild-to-severe acute respiratory syndrome conditions that required hospitalization [6].
The recently emerged severe acute respiratory system-related coronavirus-2 (SARS-CoV-2) is the causes of the current pandemic, and many efforts have been made to control the virus.
The first case of COVID-19 in Saudi Arabia was reported on March 2, 2020, in the eastern region area named Qatif. The patient was a female returning from Iraq. Later, on March 4, various prevention measures were taken by the Ministry of Health (e.g., suspension of Umrah, tourism, suspension of international flights to a number of countries, suspension of domestic flights, partial curfew for 21 days, Makkah, Madinah lockdown) to control the pandemic. Despite these restrictions, Saudi Arabia has the highest number of COVID-19 cases compared with the other Gulf countries.
According to the Saudi Press Agency, during the first wave of the COVID-19 pandemic, it has infected more than 333,193 individuals up to 27th September 2020, with 11,505 active cases in Saudi Arabia [7]. According to the Ministry of Health of Saudi Arabia, the total number of recovered cases recorded on September 27, 2020, was 317,005, with a total of 198 cities, towns, and villages reporting cases.
The Ministry of Health reported a second wave of the COVID-19 pandemic on September 29, 2020. The total number of cases recorded as of June 04, 2021, was 455,418, with a total of 438,206 recoveries (a recovery rate of 98%), and the total number of deaths was 7424 [8].
The main aim of this paper is to study the spread of the virus in Saudi Arabia based on realistic data collection and published reports. The article focuses on the time series model based on the SIR-F and age-structured SEIR model with the total number of increases in confirmed cases, recoveries, and deceased cases.
The paper is organized as follows: the SIR-F model is introduced by taking the classic SIR model with customized ODE, and its various aspects are discussed. Additionally, we presented the results of the age-structured SEIR model and our analysis of the effect of the pandemic in Saudi Arabia. This article concludes with the outcomes of our analysis and its connections to the evidence with the collected data.
Literature review
Basic SIR-F Model
A generalized SIR-F model is numerically implemented and customized with the ordinary differential equation (ODE) derived from the basic SIR model. In the basic SIR model, the total population is considered to have the possibility of susceptibility to the virus (S), infection (I) and recovery (R). Susceptible individuals were subtracted from the total population of virus carriers (confirmed by testing). In the SIR-F model, we assume that some patients might have died before going to the hospital or before testing positive. The infection rate, β, represents the velocity of the disease in the population. The transition state from S to I is always stochastic, and the model is defined as follows:
| 1 |
where S = Susceptible, S* is confirmed cases, I = Infected, R = Recovered, F = Deaths.
α1 is the mortality rate of S*, α2 is the mortality rate after the individual is affected [1/min], β = Effective constant rate [1/min], and γ = Recovery rate [1/min].
Non-dimensional SIR-F model
The ordinary differential equation of the SIR-F model is given as
| 2 |
where N is the total population, and is the contact rate at which new infections are caused when contacted with the others.
| 3 |
If is more than 1, it means that there is a high possibility of outbreak in the future, and if is less than or equal to 1, then there is no epidemic, and the virus will die without affecting a large number of populations.
Proposed model: age-structured SEIR model
Basic SEIR model
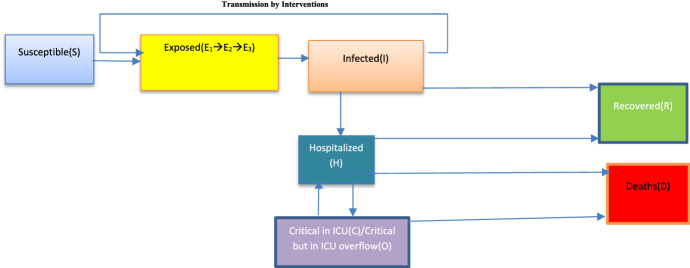
The model is described with the transmission rate parameters shown in Fig. 1.
Fig. 1.

Basic SEIR Model
Furthermore, suppose that:
µ is the equal birth and death rate,
1/α is the mean latent period for the disease,
1/γ is the mean infectious period, and the contact rate is .
This can be described by the ordinary differential equation (ODE) [9].
| 4 |
where , and is defined as
| 5 |
Individuals who become infected may experience an average R0 secondary infection while they are infectious.
The modified SEIR model
We assumed the model to be a closed system by considering the total population of Saudi Arabia to be 34,218,169, according to KAPSARC [10], including 21,103,198 Saudi citizens and 13,114,97 residents.
A group of populations are delineated by age classes with parameter a, which allows for a variable transition rate based on their age. The ODE is modified as follows [11]:
| 6 |
Susceptible individuals [S] become infected via contact with an infected individual.
Exposed individuals [E] progress toward a symptomatic state at an average time tl.
Infected individuals [I] get infected with an average of R0 secondary infections, with time ti, the infected individual either get hospitalized or recovered.
Hospitalized individuals [H] either recover or the situation of the individual worsens to a critical state with time th. The individual then progresses to either critically ill individuals in the ICU or infection leads to death.
Critical individuals [C] progress toward ICU usage; they either return to the hospital state [H] and die[D] on a time scale of tc.
Recovered individuals [R] cannot get infected again once recovered.
The parameters of the modified SEIR model (Fig. 2) fall into four categories [11].
A time-dependent infection rate
Time scale of different transitions tl(time from infection to infectiousness), ti (time either get recovers or falls severely ill), th (time infected individual get recover or deteriorates into critical state), and tc (time an individual remains critically ill or stabilize)
Age-specific parameters ma (individual mildly infected or asymptomatic), ca (individual in critical state), pa(fraction of severe cases progressing toward palliative care) and fa (fraction of critical cases that are fatal)
If the number of individuals exceeds the capacity of the ICU, the individual will be placed in an overflow category. Patients in this category give priority to the younger group to progress them toward a recovery state.
Fig. 2.
The modified SEIR model
The transmission rate is given by:
| 7 |
where is the degree where the age groups are isolated from the rest of the individuals, is the time of mitigation measure, is the amplitude of seasonal variation in transmission, and is the time at which the transmission rate is peak.
Parameter estimations
The parameters are estimated from the cumulative number of cases and the fatalities reported [11]. Since COVID-19 has more severe impacts on the elderly population, age is an important determinant of the overall burden on the health care system. Several studies have attempted to estimate the infectious transmission rate with different security measures, such as social distancing and infection control.
Population
We used the World Bank Databank datasets [12] to create the population pyramid of Saudi Arabia, as shown in Table 1. It demonstrates the general population pyramid across different age groups employing the real population pyramid.We used the World Bank Databank datasets [12] to create the population pyramid of Saudi Arabia, as shown in Table 1. It demonstrates the general population pyramid across different age groups employing the real population pyramid.
Table 1.
Population pyramid collected from the World Bank Databank
| S.No | Age_first | Age_last | Period_of_Life | School | Office | Others | Age | Population | Portion |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 2 | Nursery | 3 | 0 | 0 | 2 | 1,797,741 | 0.053055 |
| 1 | 3 | 5 | Nursery school | 4 | 0 | 1 | 5 | 1,786,702 | 0.052729 |
| 2 | 6 | 10 | Elementary school | 5 | 0 | 1 | 10 | 2,869,228 | 0.084677 |
| 3 | 11 | 13 | Middle school | 5 | 0 | 1 | 13 | 1,549,188 | 0.045720 |
| 4 | 14 | 18 | High school | 6 | 0 | 1 | 18 | 2,304,784 | 0.068019 |
| 5 | 19 | 25 | University/work | 3 | 3 | 1 | 25 | 3,477,278 | 0.102622 |
| 6 | 26 | 35 | Work | 0 | 6 | 1 | 35 | 6,503,090 | 0.191920 |
| 7 | 36 | 45 | Work | 0 | 5 | 1 | 45 | 6,834,007 | 0.201686 |
| 8 | 46 | 55 | Work | 0 | 5 | 1 | 55 | 4,187,502 | 0.123582 |
| 9 | 56 | 65 | Work | 0 | 5 | 1 | 65 | 1,894,782 | 0.055919 |
| 10 | 66 | 75 | Retired | 0 | 0 | 4 | 75 | 460,193 | 0.013581 |
| 11 | 76 | 85 | Retired | 0 | 0 | 3 | 85 | 181,034 | 0.005343 |
| 12 | 86 | 95 | Retired | 0 | 0 | 2 | 95 | 38,890 | 0.001148 |
The exploratory population parameters of COVID-19 for KSA are summarized in Table 2, and the epidemiological parameters are summarized in Table 3.
Table 2.
Population parameters
| Parameter | Value |
|---|---|
| Age distribution | Saudi Arabia |
| Case counts (Confirmed and death cases) | Saudi Arabia |
| Number of hospital beds | 70,815 |
| Number of available ICU beds | 6515 |
| Cases imported into community per day | 0.1 |
| Number of cases at the start of the simulation | 14,735 |
| Total population | 34,218,169 |
Table 3.
Epidemiology parameters
| Parameter | Value |
|---|---|
| Average time in regular ward (days) | 7 |
| Average time in ICU ward | 14 |
| Infectious period | 3 |
| Latency | 3 |
| Increase in death rate when ICU are overcrowded | 2 |
| Seasonal peak in transmissibility | June, July 2020 |
| R0 at the beginning of the outbreak | 1.7–2 |
| Seasonal variation in transmissibility | 0 |
Epidemiology
Mitigation
The study considered various control measures and intervention strategies, such as quarantine, social distancing, school and university closures, travel suspension, prohibition of social gatherings and complete lockdown. Each intervention was measured over time and compared with the baseline scenario to reduce the impact of the pandemic. Scenarios are compared with the number of confirmed cases, growth rate, peak time, and total deaths. Table 4 demonstrates the interventions starting from the first cases reported in the KSA until June 20, 2021, with a total of 15 runs.
Table 4.
Intervention with transmission rate
| Intervention Sequence | From | To | Reduction of transmission |
|---|---|---|---|
| Intervention 0 | Mar 09, 2020 | Apr 16, 2020 | 1–1% |
| Intervention 1 | Apr 16, 2020 | May 21, 2020 | 24.9–29.1% |
| Intervention 2 | May 21, 2020 | Jun 11, 2020 | 15.1–16.9% |
| Intervention 3 | Jun 11, 2020 | Jul 02, 2020 | 32.7–39.3% |
| Intervention 4 | Jul 02, 2020 | Jul 29, 2020 | 39.7–48.3% |
| Intervention 5 | Jul 29, 2020 | Aug 19, 2020 | 31.8–38.2%% |
| Intervention 6 | Aug 19, 2020 | Sep 22, 2020 | 37–45% |
| Intervention 7 | Sep 22, 2020 | Oct 13, 2020 | 30.9–37.1% |
| Intervention 8 | Oct 13, 2020 | Nov 03, 2020 | 29.2–34.8% |
| Intervention 9 | Nov 03, 2020 | Dec 07, 2020 | 38.8–47.2% |
| Intervention 10 | Dec 07, 2020 | Jan 01, 2021 | 34.4–41.6% |
| Intervention 11 | Jan 01, 2021 | Feb 01, 2021 | 16–18% |
| Intervention 12 | Feb 01, 2021 | Mar 14, 2021 | 29.2–34.8% |
| Intervention 13 | Mar 14, 2021 | Apr 17, 2021 | 20.5–23.5% |
| Intervention 14 | Apr 17, 2021 | June 20, 2021 | 30.9–37.1% |
Results
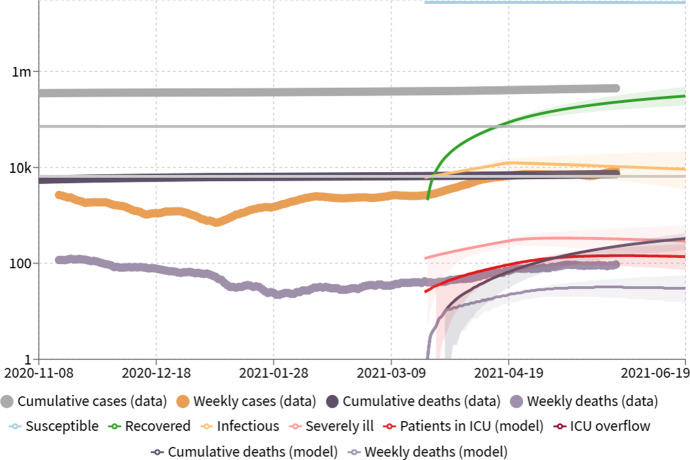
By introducing the interventions, the cumulative number of infected cases and the number of deaths were reduced, which helped decrease the effects of the epidemic by flattening the curve and decreasing the number of infected cases (Fig. 3).
Fig. 3.
Infection growth
A model [11] was developed to estimate the epidemiological parameters for the 9 different age groups, as shown in Table 5 and Fig. 3. When applied to the KSA epidemic, the model estimates that the virus had an R0 value between 1.7 and 2.
Table 5.
Age group infected distribution
| Age group | Age distribution | Confirmed % of total | Severe % of Confirmed | Palliative % of severe | Critical % of severe | Fatal % of critical | Fatal % of all infections |
|---|---|---|---|---|---|---|---|
| 0–9 | 5,956,215 | 5 | 1 | 0 | 5 | 10 | 0 |
| 10–19 | 4,860,281 | 5 | 3 | 0 | 10 | 10 | 0 |
| 20–29 | 5,354,763 | 10 | 3 | 0 | 10 | 10 | 0 |
| 30–39 | 6,980,363 | 15 | 3 | 0 | 15 | 10 | 0.01 |
| 40–49 | 6,408,790 | 20 | 6 | 0 | 20 | 10 | 0.02 |
| 50–59 | 3,216,573 | 20 | 10 | 0 | 25 | 20 | 0.1 |
| 60–69 | 1,373,521 | 25 | 25 | 5 | 30 | 30 | 0.88 |
| 70–79 | 493,856 | 20 | 35 | 10 | 25 | 40 | 2.1 |
| 80 + | 169,509 | 40 | 50 | 20 | 15 | 40 | 5.2 |
Table 5 demonstrates the distribution of age groups, which shows that individuals fall into each group when infected. The columns are summarized based on the severity informed by the epidemiological and clinical observations from China, Spain, Switzerland, and Italy.
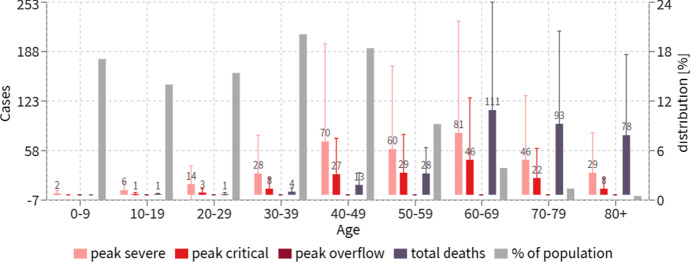
Figure 4 estimates the evolution of the KSA epidemic under the scenario where the security measures are relaxed for the younger group but kept the same within the older group. The evolution of the epidemic predicted that most deaths occurred in the older age group, even though the percentage of infections was predicted to be higher in the younger age group.
Fig. 4.
Confirmed case distribution in different age groups
Discussion
Considering the rising number of cases and deaths in the Kingdom of Saudi Arabia, several interventions have been introduced by the government, such as social distancing, prohibiting social gatherings with no more than twenty individuals, temporary bans on dine in restaurants and international travel bans. The SIR-F model is improved by closure and lockdown to investigate the effect of interventions with the closure of educational institutions and the market. Forecasting and uncertainty have been proposed to be integral parts of the decision-making process [13].
Regarding the implementation of an intervention, the effect was predicted for the spread of virus with a simulation run of 700 days starting from the date when the first case was recorded [14]. The study analyzed the virus peak and size of the pandemic in the Kingdom and estimated that the virus would be under control by the end of June 2021, as shown in Fig. 5 [14].
Fig. 5.

Predicted number of cases with closure and lockdown using the SIR-F model for 700 days
The study verifies that the infection curve decreased in April 2021 and that the pandemic period will end in April 2022. Additionally, Fig. 6 shows that for the fifth phase is decreasing but is far from the end of the epidemic [14].
Fig. 6.

Worst-case scenario using the SIR-F Model
In our present study, we focused on close observation of interventions by categorizing the individuals into different age groups. To control the spread of the virus, we need to keep the effective reproduction number below one. We have proposed a modified SEIR model to observe overflow in (C/O) situations to monitor the infection rate closely and to avoid overflows in the ICU by observing infections in different age groups. Table 5 demonstrates that the effect of the virus on the elderly age group with the highest fatal percentage rate of infections was very high compared with the other age groups. Since the virus has a more severe effect on elderly individuals, plans and policies for intervention strategies can be developed, encompassing early detection through surveillance and diagnosis. In response to the increase in the number of daily cases and to control the pandemic, Saudi Arabia launched the COVID-19 vaccination drive on December 17, 2020, after the Saudi Food and Drug Authority (SFDA) approved the registration of the Pfizer-BioNTech vaccine. During the campaign, elderly individuals over the age of 65, those suffering from chronic diseases, and front-line health workers were given priority. The second vaccination phase began on February 18, 2021. The second vaccine, Oxford-AstraZeneca, was approved by the Saudi Food and Drug Authority (SFDA) and made available for all Saudi citizens and expatriates. Free vaccine shorts were distributed throughout the kingdom. The Ministry of Health announced on May 30, 2021, that 40% of the Kingdom’s population had received at least one dose of a COVID-19 vaccine administered across 587 vaccination centers [15]. The government of Saudi Arabia aims to complete the vaccination campaign drive before the end of 2021. As a result, future research can analyze a further decrease in the infection rate, a decrease in the parameter [14], and the mitigation of the pandemic at an earlier date.
Acknowledgements
This research is done with the financial support by the Deanship of Scientific Research at King Khalid University under research grant number (RGP.1/210/42).
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Kuldeep Dhama, Sharun Khan, Ruchi Tiwari, Shubhankar Sircar, Sudipta Bhat, Yashpal Singh Malik, Karam Pal Singh, Wanpen Chaicumpa, Katterine Bonilla-Aldana D, Alfonso J (2019) Coronavirus Disease 2019–COVID-19. https://cmr.asm.org/content/33/4/e00028-20. [DOI] [PMC free article] [PubMed]
- 2.Zhu N, Zhang D, Wang W, Li X (2020) A novel coronavirus from patients with pneumonia in China. N Engl J Med 382:727–733. [DOI] [PMC free article] [PubMed]
- 3.Ghinai I, McPherson TD, et al. First known person-to-person transmission of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) in the USA. Lancet. 2020;395(10230):1137–1144. doi: 10.1016/S0140-6736(20)30607-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Pung R, Chiew CJ, Young BE, et al. Investigation of three clusters of COVID-19 in Singapore: implications for surveillance and response measures. Lancet. 2020;395(10229):1039–1046. doi: 10.1016/S0140-6736(20)30528-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Peiris JS, Guan Y, Yuen KY. Severe acute respiratory syndrome. Nat Med. 2004;10:S88–S97. doi: 10.1038/nm1143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.World Health Organization, Global Alert and Response (GAR): “Coronavirus infections”. https://www.who.int/health-topics/middle-east-respiratory-syndrome-coronavirus-mers#tab=tab_1
- 7.Health Ministry Spokesperson: The official Saudi Press Agency. https://www.spa.gov.sa/viewfullstory.php?lang=en&newsid=2138772
- 8.Saudi Arabia Coronavirus disease (COVID-19) situation−KAPSARC Data Portal: https://datasource.kapsarc.org/explore/dataset/saudi-arabia-coronavirus-disease-covid-19-situation/information/?disjunctive.daily_cumulative&disjunctive.indicator&disjunctive.event&disjunctive.city_en&disjunctive.region_en
- 9.Hamdy M. Youssef, Najat A. Alghamdi, Magdy A. Ezzat, Alaa A. El-Bary, Ahmed M. Shawky (2020) A modified SEIR model applied to the data of COVID-19 spread in Saudi Arabia” 10.1063/5.0029698 [DOI] [PMC free article] [PubMed]
- 10.https://datasource.kapsarc.org [Google Scholar]
- 11.https://covid19-scenarios.org/
- 12.https://data.worldbank.org/
- 13.Petropoulos F, Makridakis S. Forecasting the novel coronavirus COVID-19. PLoS ONE. 2020;15(3):e0231236. doi: 10.1371/journal.pone.0231236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Saad Awadh Alanazi, Kamruzzaman MM, Madallah Alruwaili, Nasser Alshammari, Salman Ali Alqahtani, Ali Karime (2020) Measuring and Preventing COVID-19 using the SIR model and machine learning in smart health care. J Healthcare Eng, Article ID 8857346, 12 p. 10.1155/2020/8857346 [DOI] [PMC free article] [PubMed]
- 15.% of Saudi population has taken at least one vaccine shot - Saudi Gazette