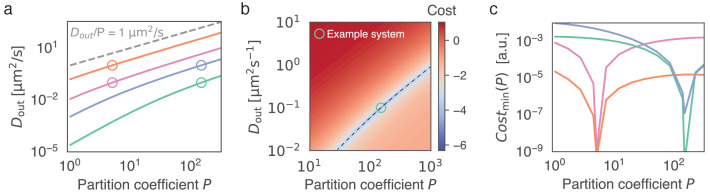
Figure 5. Given the recovery dynamics inside a condensate, the key parameters $D_{\text{𝐢𝐧}}$, $D_{\text{𝐨𝐮𝐭}}$ and $P$ can in theory be determined uniquely without measuring the outside dynamics, using Equation (6).

(a) Given the partition coefficient $P$, $D_{\mathrm{out}}$ is found by fitting the model to synthetically generated example data. As example systems, indicated by open circles, we consider in silico data, obtained by solving Equation (6) with known parameters $P$ and $D_{\mathrm{out}}$. To mimic the approach of initially determining $D_{\mathrm{in}}$ (see Figure 1) we keep ${\displaystyle D_{in}=0.01\mu {\mathrm{m}}^2{\mathrm{s}}^{-1}}$ for all in silico datasets. For each example system (open circles), the best fitting $D_{\text{out}}$ is found given a range of $P$ (solid lines). Parameters used were as follows: pink circle: ${\displaystyle D_{out}=0.1\mu {\mathrm{m}}^2{\mathrm{s}}^{-1}}$, $P=5$, orange circle: ${\displaystyle D_{out}=1\mu {\mathrm{m}}^2{\mathrm{s}}^{-1}}$, $P=5$, green circle: ${\displaystyle D_{out}=0.1\mu {\mathrm{m}}^2{\mathrm{s}}^{-1}}$, ${\displaystyle P=150}$, blue circle: ${\displaystyle D_{out}=1\mu {\mathrm{m}}^2{\mathrm{s}}^{-1}}$, $P=150$. (b) Cost function (colorbar, log-scale) as a function of $D_{\mathrm{out}}$ and $P$. We note that the global minimum coincides with the parameters used to generate the synthetic data (green circle). The valley in parameter space (dashed line) corresponds to the green line in (a). (c) Minimum of cost function for each $P$, corresponding to curves shown in (a). This minimum corresponds to the valley indicated by the dashed line in (b). Note the minimum at the input parameter set, which indicates uniqueness of the outside dynamics for given values of $D_{\mathrm{out}}$ and $P$.