Abstract
Convection-enhanced delivery (CED) is an investigational therapy developed to circumvent the limitations of drug delivery to the brain. Catheters are used in CED to locally infuse therapeutic agents into brain tissue. CED has demonstrated clinical utility for treatment of malignant brain tumors; however, CED has been limited by lack of CED-specific catheters. Therefore, we developed a multiport, arborizing catheter to maximize drug distribution for CED. Using a multiphasic finite element (FE) framework, we parametrically determined the influence of design variables of the catheter on the dispersal volume of the infusion. We predicted dispersal volume of a solute infused in a permeable hyperelastic solid matrix, as a function of separation distance (ranging from 0.5 to 2.0 cm) of imbedded infusion cavities that represented individual ports in a multiport catheter. To validate the model, we compared FE solutions of pressure-controlled infusions to experimental data of indigo carmine dye infused in agarose tissue phantoms. The Tc50, defined as the infusion time required for the normalized solute concentration between two sources to equal 50% of the prescribed concentration, was determined for simulations with infusion pressures ranging from 1 to 4 kPa. In our validated model, we demonstrate that multiple ports increase dispersal volume with increasing port distance but are associated with a significant increase in infusion time. Tc50 increases approximately tenfold when doubling the port distance. Increasing the infusion flow rate (from 0.7 μL/min to 8.48 μL/min) can mitigate the increased infusion time. In conclusion, a compromise of port distance and flow rate could improve infusion duration and dispersal volume.
Keywords: biphasic finite element analysis, agarose gel, infusion, solute transport, multiport catheter, convection-enhanced delivery
Introduction
Convection-Enhanced Delivery.
Glioblastoma (GBM) is a highly aggressive form of astrocytic brain cancer responsible for 46.6% of malignant brain tumors [1]. Standard treatment consisting of surgery followed by adjuvant radiation is only partially effective. Treatment rarely eliminates the entire primary tumor resulting in continued growth, or regrowth, from distantly infiltrating malignant cells [2–4]. These malignant cells are often intrinsically resistant to available chemotherapeutic agents and significantly reduce the efficacy of drug treatments [5,6]. Furthermore, overcoming the blood brain barrier and blood tumor barrier to achieve sufficient drug concentration at the treatment site remains a challenge [7,8]. Thus, prognosis is poor with median patient survival time of 15 months and mortality rates exceeding 95% for 5 years postdiagnosis [9].
One promising approach to circumvent the blood brain barrier is convection-enhanced delivery (CED), which involves intracranial infusion of therapeutic agents via a small catheter inserted into the brain parenchyma [10–12]. With this technique, high concentrations of large molecular-weight compounds can be delivered to larger regions of the brain compared to diffusion-dependent therapies [10]. Preclinical and early phase clinical trials of CED showed promising results for treatment of malignant brain tumors, specifically GBM [13–18]. However, a phase III clinical trial (known as the PRECISE trial) using CED to treat GBM failed to meet its clinical endpoints. In the PRECISE trial, patients with recurrent GBM were treated with a targeted pseudomonas-based exotoxin, cintredekin besudotox (CB), delivered intracranially using 2–4 commercially available, single-port catheters. Overall survival for the patients treated with CED, compared to the survival of patients treated with carmustine-impregnated implants (Gliadel), showed no significant improvement [19]. Follow-up analyses of the drug distribution using a computational software revealed that the predicted dispersal volume of CB was well below the intended volume target. On average, only 20% of a 2-cm penumbra surrounding the resection cavity was targeted with the cytotoxin [20]. It was hypothesized that the suboptimal outcomes of the trial were linked to the poor coverage achieved during the infusions, suggesting that better delivery of therapeutic agents to the target tissue volume may improve CED.
The PRECISE trial highlighted the need for better delivery systems. CED infusion poses unique challenges that must be addressed with CED-specific catheter technologies. For example, a common drawback of CED is reflux of drug along the insertion tract, which results in ineffective drug distribution and premature termination of the CED therapy. Thus, reflux-arresting properties such as a “step change,” in which the diameter of the catheter changes along the distal tip of the catheter, are incorporated in investigational CED-specific catheters [21–25]. Another major challenge of treating GBM is the highly infiltrative nature of the disease. Malignant cells extend centimeters beyond the resolvable tumor mass, deep into the surrounding healthy tissue. Clinical recurrences of the primary tumor in the adjacent areas necessitate extended delivery to treat infiltrative cells [26]. With the focus for extending the dispersal volume of the infusate for CED, Infusion Therapeutics, Inc., (Cleveland, OH) designed a catheter (Cleveland Multiport Catheter™) that offers multiple ports of infusion originating from a single insertion tract [27]. Others have opted for a different approach and are investigating intermittent, chronic delivery of therapeutics using catheters that are permanently implanted and accessed via a port on the side of the cranium [28].
Arborizing Catheter.
Our research group developed the “arborizing catheter” to achieve broad drug dispersal volume (Fig. 1). The catheter consists of a primary cannula approximately 3 mm in outer diameter. From the primary cannula, hollow optical fibers deflect around the axis of the last undeflected optical fiber at the center. Each fiber, termed “microneedle”, is a fluid port, inserted individually into the tissue at the desired depth to direct the dispersal of the infused drug. To evaluate the performance of the arborizing catheter compared to single-port catheters, we conducted infusion studies which are described elsewhere [29]. Briefly, we quantified volume dispersed (Vd) and mean distribution ratio (volume dispersed to total volume infused: Vd:Vi) of indigo carmine dye infused in 0.6% (w/w) agarose gels for three experimental groups (Table 1). Results showed that the arborizing catheter is advantageous at increasing Vd over a single-port catheter. However, Vd:Vi, which can be thought of as an effectiveness value of drug dispersal, was lower than expected for the arborizing catheter. This is possibly due to too much overlap in the distribution volume from each microneedle. Using computational models to test various design concepts is an economical and effective approach to optimize the design of the arborizing catheter. Thus, the goal of this study is to use computational models to simulate infusion conditions and parametrically explore how the separation distance of adjacent microneedles in the arborizing catheter and flow rates affect dispersal volume.
Fig. 1.
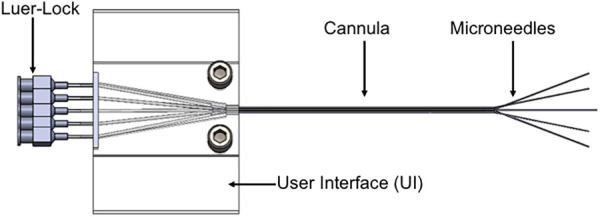
Schematic of the arborizing catheter, showing multiple ports or microneedles deflected from the primary cannula
Table 1.
Summarized results of Vd (volume dispersed) and Vd:Vi (volume dispersed:volume infused) for three experimental groups for 100 min long infusions in agarose tissue phantoms
| Results | |||||
|---|---|---|---|---|---|
| Group (n = 5) | Flow rate (μL/min) | No. of ports | Total Vi (μL) | Vd (ml) | Vd:Vi |
| Single-port-slow | 1 | 1 | 100 | 2.4 ± 0.2 | 23.6 ± 2.1 |
| Single-port-fast | 7 | 1 | 700 | 5.1 ± 0.6 | 7.3 ± 0.8 |
| Arborizing catheter | 1 | 7 | 700 | 10.5 ± 1.1 | 14.9 ± 1.5 |
Methods
Biphasic With Solute Theory.
The biphasic-solute model, based on the theory of incompressible mixtures, consists of a permeable solid matrix, a solvent, and a solute. We assume the volume fraction of the solute is negligible compared to the solid and solvent fractions. In addition, the friction within the fluid (i.e., solvent and solute viscosity) is assumed negligible relative to the friction between the solid and solvent (i.e., permeability). The complete derivation of the governing and constitutive equations can be found in the published literature [30–33].
In our biphasic finite element (FE) model, the solid phase representing the porous tissue phantom made from 0.6% (w/w) agarose gel is denoted as α = s, the solvent represents de-ionized water (α = w), and the solute (or infusate) represents indigo carmine (MW ∼ 446 Da, α = a). We assumed that all constituents are neutrally charged and intrinsically incompressible; thus, the true density ( ) is invariant for each constituent. Using the generalizations for the balance of linear momentum, along with the constitutive equations for the mixture stress [34], and using the solvent and solute electrochemical potentials presented in Mauck et al. [30] result in the following momentum equations for the mixture, solvent, and solute, respectively,
| (1) |
| (2) |
| (3) |
where p is the fluid pressure, σe is the elastic solid stress in the matrix, φw is the volume fraction for the solvent, R is the universal gas constant, θ is the absolute temperature, and c is the concentration of the solute on a solution-volume basis. Additionally, vα is the velocity of the constituent α, and fαβ is the diffusive drag force between the constituents α and β (with fαβ = fβα). The nonzero diffusive drag coefficients are related to the hydraulic permeability (k) of the solvent through the solid matrix, the solute diffusivity in the mixture (D), and the solute diffusivity in the free solution (D0) [31] by
| (4) |
The governing equations for mass balance of the mixture, solvent, and solute phases, in the absence of chemical reactions, are
| (5) |
| (6) |
where ρα = φα is the apparent density for the constituent α, and φα is the volume fraction for each constituent. Inverting the balance of linear momentum equations (2) and (3) yields expressions for the volumetric fluid flux, and solute molar flux, as functions of their respective driving forces utilizing relations of the permeability and diffusivity to diffusive drag coefficients described in Ateshian et al. [32] and Mass et al. [33].
Model Validation.
To validate the above model, we compared dispersal volume of indigo carmine dye in agarose from infusion experiments to numerical predictions of solute dispersal in a biphasic medium from pressure-driven infusion simulations. The geometry for the model consists of a cube with an embedded spherical cavity of initial radius r0 = 0.18 mm, which corresponds to the inner diameter of a 28-gauge hypodermic needle. The solid matrix is modeled as a homogeneous, isotropic, neo-Hookean solid. The neo-Hookean model is a hyperelastic material model that, for small strains and rotations, reduces to the linear elasticity model. The FE implementation of this material requires the modulus of elasticity (E) and Poisson's ratio (ν) to be defined. Material properties for agarose were chosen: E = 6 kPa and ν = 0.4 [35]. The solid volume fraction (φs) is based on the volume fraction of fibers for the 0.6% agarose gel [36]. Consistent with literature reports, we model the hydraulic permeability tensor as a function of local porosity changes [37]. Specifically, we use the following relationship proposed by Holmes–Mow for the strain-dependent permeability tensor:
| (7) |
where k0 is the isotropic hydraulic permeability in the reference state, M is the exponential strain-dependence coefficient, β is the power-law exponent, and J is the Jacobian of the deformation gradient, i.e., J = det (F).
Due to the limited literature data for agarose gels, parameters based on previous brain tissue analyses were chosen: k0 = 4.5 mm4/N s, β = 0, and M = 1. The power-law exponent, β = 0, was used to reduce the Holmes–Mow permeability model to the exponential relationship obtained by Lai and Mow [38] consistently used in the literature to model hydraulic permeability in brain tissue. We chose M = 1 for this model, which is within the range of 0–5 that has been used in previous infusion simulations [39–41]. Finally, k0 = 4.5 mm4/N s was chosen parametrically to achieve agreement between the experimental and simulation results. Its magnitude is in agreement with hydraulic permeability values measured in white matter, 2% (w/vol) agarose gel, and those previously used to model brain tissue [39,40,42,43]. Free and effective diffusivity are assumed nearly equivalent and prescribed a value of 6.0 × 10−4 and 5.4 × 10−4 mm2/s, based on the molecular size for indigo carmine in water and extrapolated for room temperature (298 K) using Einstein's relation for diffusivity [44].
For the model, we assume that all the outer tissue surfaces are exposed boundaries to ambient pressure (zero interstitial pressure and traction free boundary conditions). Taking advantage of symmetry, only an eighth of the geometry was considered for the simulations. The boundary conditions at the symmetry faces include zero displacement, fluid flux, and mass flux. Similar to Chen and Sarntinoranont [40], we assume zero contact stress (σe = 0) applied to the solid matrix at the porous–fluid interface. To guarantee continuity across element boundaries, we prescribe the effective fluid pressure rather than the interstitial fluid pressure (p), where R is the universal gas constant, is the absolute temperature, is the osmotic coefficient, and c is the solute concentration [33]. Infusion pressure (i.e., the effective fluid pressure) was prescribed to the spherical boundary of the cavity to induce an average flow rate of approximately 1 μL/min and 7 μL/min and compared to experimental data [29]. Infusion pressure was ramped rapidly with ramp time (t0) of 1 s and held constant for the duration of each simulation. Solute concentration is only continuous across an interface in the case of ideal solubility; thus, we solve for the effective solute concentration ( ) instead [45]. The arising boundary value problem was solved with FEBio (version 2.6.42).
We used PreView (version 1.202) to create a mesh consisting of eight-node trilinear hexahedral elements with a mesh bias toward the infusion cavity. The effective solute concentration present in the solid was compared to the prescribed concentration at the infusion cavity in a mesh convergence study. Increasing the number of elements decreased the percent error between the prescribed concentration and the max concentration of elements at the boundary of the infusion cavity. A mesh with 1296 elements, biased toward the infusion cavities, resulted in less than 1% error for the simulations. Thus, meshes for all the simulations were at least 1296 elements.
We normalized the effective solute concentration values given by the FE solution and used a threshold of 0.1% of the normalized effective solute concentration ( n) to calculate Vd. We chose the threshold based on experimental calibration of grayscale intensity threshold values to known serial dilutions of 5% (w/w) stock concentration of indigo carmine with 0.6% agarose gel. This resulted in uniform gels of known concentrations of indigo carmine ranging from 0 to 1% of the stock solution. We captured images of the gels in similar lighting as the original experimental infusions. We then converted these images into grayscale images normalized to intensity values ranging from 0.0 (black) to 1.0 (full intensity or white). Global intensity threshold values were calculated (using a matlab algorithm based on Otsu's method) for each image. The calculated Vd from the simulations for time 20–100 min were compared with derived Vd from experiments for the same infusion duration.
Parametric Simulations.
After the validation of our FE model, we simulated infusions using two individual ports from a multiport catheter. Our model geometry was adjusted to include two infusion cavities, representing catheter source ports (Fig. 2). The sources are spaced along the x-axis at a separation distance (d) ranging from 0.5 to 2.0 cm as measured from the center of each cavity. The y, z length dimensions for the cube are equal to the separation distance, which was approximately 275-times greater than r0. This ensures that changes in interstitial pressure, displacement, and fluid velocity are negligible beyond such a distance from the infusion site [46,47].
Fig. 2.
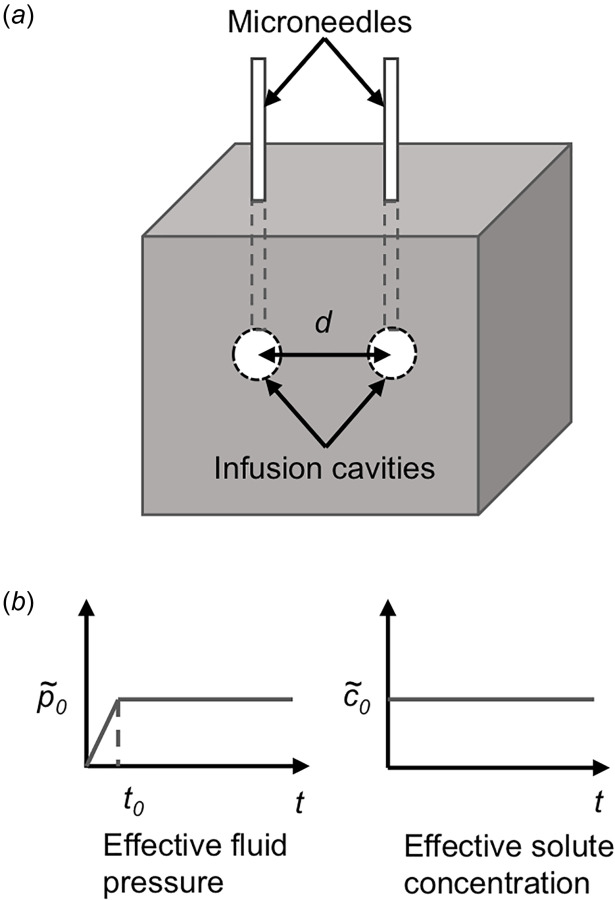
(a) FE model geometry of the biphasic solid with two embedded infusion cavities (i.e., source ports) and (b) constant infusion pressure applied at a rapid ramp time of t0 and constant effective solute concentration were applied at the inner surface boundary of the infusion cavities. Zero interstitial pressure and traction free surface boundary conditions were applied at the outer boundaries of the solid.
Magnitude for the infusion pressure was varied between 1 and 4 kPa depending on the experimental protocol. At the higher infusion pressures, lowering v helped achieve convergence of the model. Thus, v ranged from 0.35 to 0.4. Additionally, a constant effective solute concentration was prescribed at the spherical boundary of the cavities. Table 2 presents a summary of the biphasic finite element model parameters for this study.
Table 2.
Summary of baseline material parameters used in this study
| Parameter | Value |
|---|---|
| Young's modulus, E | 6000 Pa |
| Poisson's ratio, v | 0.35–0.4 |
| Initial hydraulic permeability, k0 | 4.5 mm4 N−1 s−1 |
| Nonlinear hydraulic permeability parameter, M | 1 |
| Solid volume fraction, φs | 0.006 |
| Free diffusivity, D0 | 6.0 × 10−4 mm2 s−1 |
| Effective diffusivity, D | 5.4 × 10−4 mm2 s−1 |
| Temperature, T | 298 K |
| Infusion pressure ramp time, t0 | 1 s |
| Prescribed initial pressure, p0 | 1–4 kPa |
| Separation distance, d | 0.5–2 cm |
| MW, indigo carmine | 466 Da |
We calculated the volumetric flow rate utilizing the resultant deformation of the infusion cavity per time-step and the flux with the current surface area of the cavity. Because the volumetric flow rate is a function of time, we averaged the values from t0 to 100 min for each simulation. Additionally, we defined and computed Tc50 as the infusion time for the effective solute concentration at the midpoint between the two infusion cavities to be 50% (or 0.5) of the prescribed solute concentration at the infusion cavities.
Results
Figure 3(a) shows the intensity threshold values corresponding to the known diluted concentrations of the dye stock solution. The intensity threshold used to calculate Vd for the infusion experiments was 0.22 ± 0.03, which corresponds to a concentration of 0.09% of the stock solution. Therefore, we used 0.1% of the normalized effective concentration as a threshold to calculate Vd in the FE simulations. Vd values were calculated from simulations for continuous infusion ranging from 20 to 100 min and compared with single-port experimental infusions as shown in Fig. 3(b). The simulation labeled “FE 1 μL/min” resulted in an average flow rate of 0.99 μL/min and was compared to the single-port infusion experiments conducted at a flow rate of 1 μL/min. The results indicate good agreement at all time points. The percent difference between the average Vd for experiments and the FE model is <4%, for time 60–100 min, but higher at earlier time points. For the 20- and 40-min time points, the percent difference is 11.0% and 6.0%, respectively. However, this difference falls below one standard deviation of the measured experimental values. Similarly, Vd derived from the FE simulation labeled “FE 7 μL/min” resulted in an average flow rate of 6.92 μL/min and were compared to the Vd measured from single-port infusion experiments at 7 μL/min. They also show good agreement with a percent difference of <5.5% for all time points.
Fig. 3.
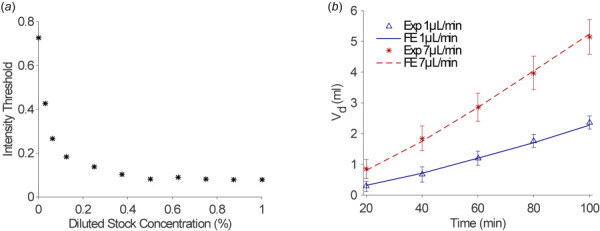
(a) Indigo carmine stock solution (5% w/w) was serially diluted from 1:100 in an agarose solution and plotted as percentages versus their corresponding grayscale intensity threshold values from postprocessed images and (b) volume dispersed, Vd (milliliter), plotted versus time (minutes) for FE simulations compared to infusion experiments (Exp) for two flow rates (1 μL/min and 7 μL/min)
Figure 4 shows the prescribed infusion pressures ranging from 1 to 4 kPa versus the resultant average flow rates calculated after the rapid ramp time of 1 s and up to 100 min. Consistent with Chen and Sarntinoranont [40], we found that the predicted relation between infusion pressure and the average flow rate was nonlinear. Small changes in infusion pressure resulted in greater changes in the average flow rate. The minimum flow rate achieved by 1 kPa was 0.72 μL/min and the maximum flow rate, 8.48 μL/min, was achieved at the infusion pressure of 4 kPa. By comparison, clinically relevant flow rates for CED range from 0.5 to 10 μL/min [13,16,19,46,48,49]. Infusion pressure of 1.3 kPa and 3.5 kPa resulted in an average flow rate of 0.99 μL/min and 6.92 μL/min, respectively. These infusion pressures were prescribed for validating the model by comparing with infusion studies performed at a constant flow rate of 1 μL/min and 7 μL/min. The percent error between the average flow rates results from the FE simulation and the experimental flow rates is 1.14% and 1.04% for the 1 μL/min and 7 μL/min flow rates, respectively.
Fig. 4.
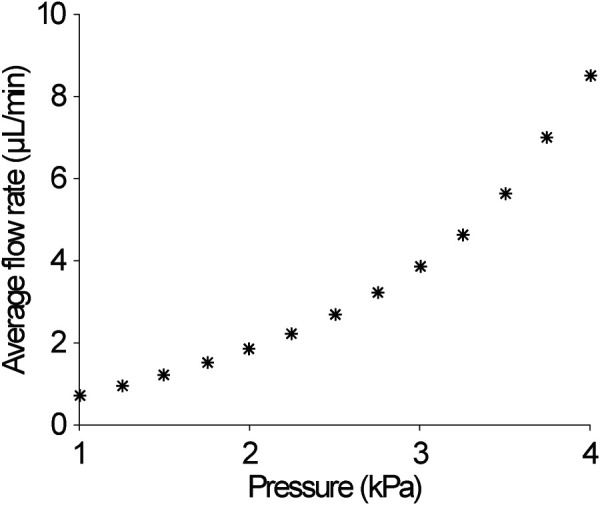
Prescribed infusion pressure versus resultant average infusion flow rates. Flow rates were calculated after the pressure was applied at a rapid ramp to the boundary of the infusion cavity.
Figure 5 demonstrates the simulation results for infusion pressures ranging from 1 to 4 kPa for infusion cavities spaced 1.5 cm apart (center to center). Due to symmetry, only an eighth of the geometry is represented in the model. The two infusion cavities are shown in the bottom corners. Contour plots show the spatial distribution of n at 300 min of continuous infusion. At this time, the simulations prescribed 1 kPa and 2 kPa show an area between the two sources in which the n is below 10% or 0.1. For these infusions, 300 min of continuous infusion would not be sufficient for complete coverage of the volume target if a concentration >10% of the infused therapeutic agent was required for efficacy. At 300 min, some overlap in the spatial distribution of the solute concentration between the two sources is demonstrated for the 3 kPa case. Finally, the 4 kPa case achieves significant overlap between the two sources with n >50%.
Fig. 5.
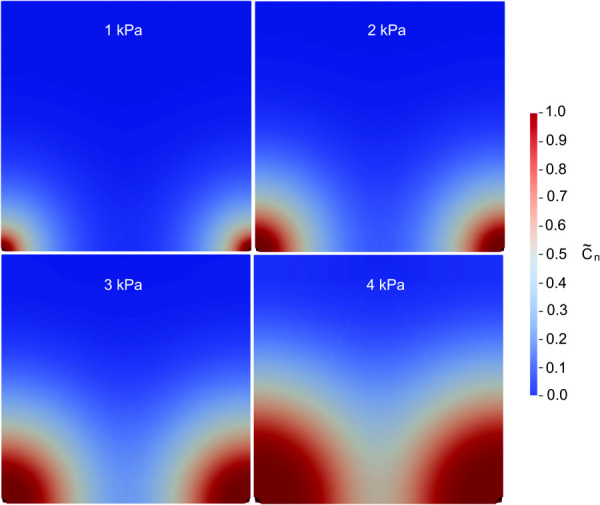
Representative color maps for simulation with source ports (infusion cavities) spaced 1.5 cm apart for infusion pressures ranging from 1 kPa to 4 kPa. The color map shows the normalized effective solute concentration at time = 300 min.
For each simulation, the calculated Tc50 indicates the time at which the concentration overlap at the midpoint between the sources reached 0.5% or 50% of the prescribed concentration at the infusion cavities. Figure 6 shows a summary of the parametric results indicating Tc50 values (in hours) as a function of port separation distance for various flow rates. As the separation distance increases, Vd increases. However, Tc50 drastically increases as shown by the two orders of magnitude change in the logarithmic scale of the y-axis (approximately 100 h). Lowering Tc50 to a more manageable total procedure time would require infusion flow rates to be increased. For example, increasing infusion pressure from 1 to 4 kPa will result in ten times higher flow rate, which would decrease the Tc50 by approximately 32 h. This is at the cost of lowering Vd:Vi as we found in infusion experiments (Table 1).
Fig. 6.
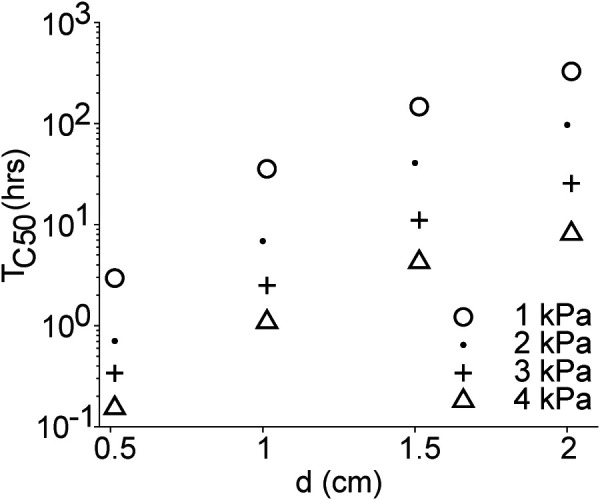
Time (hours) required for the normalized effective concentration between sources to reach 50% of the prescribed concentration at the sources (Tc50) versus the port separation distance, d (centimeter)
In this study, we chose to define Tc50 when n midway between the two sources reached 50%. However, this concentration is somewhat arbitrary as the minimum effective dose is specific to the therapeutic agent. Therefore, we performed a separate analysis to understand the time required to reach a distribution overlap at various solute concentrations between the source ports. Figure 7 shows the time, in hours, required for the solute concentration overlap ranging from 0.1 to 0.5 for port distance ranging from 0.5 to 2 cm and infusion pressures ranging from 1 to 4 kPa. Prescribed infusion pressures, and subsequently, the average flow rate of the infusion, have a greater influence at higher concentration thresholds and at greater separation distances. Additionally, doubling the separation distance between the ports achieves approximately a tenfold increase in time required to reach the specified concentration.
Fig. 7.
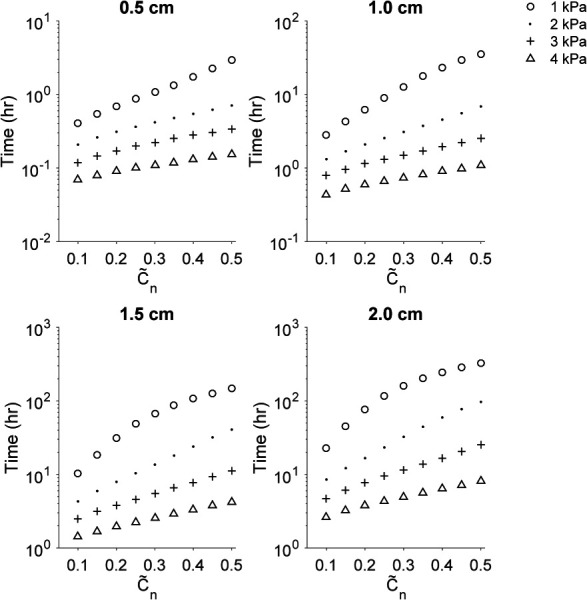
Time to reach a concentration overlap (ranging from 0.1 to 0.5 of the normalized effective solute concentration) midway between two sources for port separation distance ranging from 0.5 to 2.0 cm
Discussion
In this study, we were interested in understanding how the separation distance of two infusion ports and their prescribed flow rates would influence the dispersal volume and duration of infusion. Maintaining the treatment duration within a manageable period is important for a number of reasons. Chronic CED may be beneficial to achieve large Vd, even with lower infusion rates; however, it has not gained wide acceptance and to the best of our knowledge has only been performed in humans outside of the United States. Due to the highly invasive and permanent nature of the procedure, it requires highly specialized infusion equipment for long-term use. Short-term infusions seem to be the more common approach to CED. In the PRECISE trial, CB was administered over 96 h using 2–4 catheters at a total flow rate of 12.5 μL/min, which would result in a flow rate ranging from 3.13 to 6.25 μL/min per catheter [19]. Even if the infusion is continuous over a period of days, it does not guarantee that the therapeutic agent reaches all the affected tissue as revealed in the study conducted by Sampson et al. [20]. Therefore, a more effective approach could be to co-infuse the therapeutic with an imaging marker and perform CED under continuous imaging surveillance such as with magnetic resonance imaging (MRI). Feedback of the spatial distribution of the therapeutic can help guide the therapy to ensure proper coverage of the intended volume target [50–52]. Although this method would be an improvement over “blind” CED, the cost associated with continuous time in the MRI scanner room would undoubtedly increase the overall cost of treatment. Therefore, optimizing the treatment duration would help reduce the cost of the treatment along with reducing overall patient discomfort.
A second option to decrease time of treatment is to decrease the distance between the two ports, however, that would also reduce Vd. Thus, in order to maintain good coverage of tissue volume, more ports would be required, which supports the advantage of using a multiport catheter. Finally, infusing at higher flow rates may help decrease infusion time, but it comes at the expense of reducing Vd:Vi [53]. However, given the high recurrence rates of GBM, maximizing Vd to ensure treatment of infiltrated disease may be more important than maximizing Vd:Vi. With development of targeted drugs and drugs with a wide therapeutic index, peripheral damage of healthy brain tissue is less of a concern when attempting large Vd [54–56]. Nevertheless, higher flow rates may be at risk of inducing adverse effects such as reflux of the infusate along the catheter insertion tract [46].
The prescribed material properties in our model are based on agarose gels, given that we validated our model using experimental data from infusions in agarose tissue phantoms. Although agarose has been commonly used as a substitute for brain tissue in infusion studies [57,58], the isotropic, homogenous, and simple geometry of the phantom are very different from the brain. Computed diffusion tensor MRI demonstrates that resistance to flow is anisotropic and heterogeneous in the brain, with white matter having higher hydraulic permeability than gray matter [11,59]. In addition, abnormal tissue properties in tumor tissue, such as increased tissue stiffness and greater resistance to flow, provide additional heterogeneity that was not accounted for in this model [60,61]. Our model also neglects perfusion and low-pressure sinks, such as the ventricles and subarachnoid space of the brain. To improve upon this model, both material and geometrical heterogeneity of brain and tumor tissue should be considered. Furthermore, future studies could benefit from validating the model using data from experimental infusions in ex vivo brain tissue.
Another limitation of the study is that the model does not take into consideration the tissue deformation that may occur due to the insertion of the catheter or any reflux, or backward flow, along the insertion tract that is a common issue in CED. To induce flow, we prescribed a constant interstitial pressure at the infusion cavity boundary. However, during CED, a programmable syringe pump is used to control the flow rate of the infusion. For the flow-controlled case, the interstitial pressure of the cavity is unknown initially; thus, a constant flow rate cannot be prescribed directly with current FE analysis software. Instead, custom-written FE code or additional steps are required to circumvent the nonlinear boundary condition [62]. We are currently working on implementing a flow-controlled version of our model. Nevertheless, the model presented in this study was useful for elucidating how factors of CED therapy, such as infusion flow rate and separation distance of individual ports, influence the distribution of an infused solute in a biphasic material. Additionally, it provided a sense of the design constraints when considering the time that would be required for each infusion given a desired spatial distribution of the infusate.
Conclusions
The infiltrative nature of GBM requires maximizing the dispersal volume of the infused therapeutic to increase the efficacy of CED. Therefore, we must optimize the drug delivery technology for CED in order to make it a viable therapy for GBM. In this study, we found that using multiple ports can be advantageous in increasing the dispersal volume of infused solutes in biphasic material, such as the brain. Increasing the separation distance of individual ports can help increase Vd. However, doubling the separation distance of source ports will require approximately ten times longer for the solute spatial distribution between sources to reach a desired concentration. Increasing the flow rate of the infusion mitigates this effect, although caution is required as higher flow rates may aggravate reflux. Finally, a compromise of port separation distance and flow rate could optimize both infusion duration and Vd. Such optimization would require clinical guidance and/or adjustment of the treatment parameters based on imaging feedback.
Footnotes
Contributor Information
Egleide Y. Elenes, Department of Biomedical Engineering, , University of Texas at Austin, , 107 W. Dean Keeton Street, Stop C0800, , Austin, TX 78712 , e-mail: eelenes@utexas.edu
Manuel K. Rausch, Department of Aerospace Engineering and , Engineering Mechanics, , University of Texas at Austin, , 2617 Wichita Street, Stop C0600, , Austin, TX 78712-1221; , Department of Biomedical Engineering, , University of Texas at Austin, , 107 W. Dean Keeton Street, Stop C0800, , Austin, TX 78712 , e-mail: manuel.rausch@utexas.edu
Christopher G. Rylander, Department of Mechanical Engineering, , University of Texas at Austin, , 204 E. Dean Keeton Street, Stop C2200, , Austin, TX 78712-1591; , Department of Biomedical Engineering, , University of Texas at Austin, , 107 W. Dean Keeton Street, Stop C0800, , Austin, TX 78712 , e-mail: cgr@austin.utexas.edu.
Funding Data
National Cancer Institute (P01 CA207206-01; Funder ID: 10.13039/100000054).
Nomenclature
- c =
concentration of the solute on a solution-volume basis (nmol/mm3)
- n =
normalized effective solute concentration
- d =
separation distance between adjacent infusion sources or ports (cm)
- D =
effective diffusivity (mm2/s)
- D0 =
free diffusivity (mm2/s)
- E =
Young's modulus (kPa)
- fαβ =
the diffusive drag force between the constituents α and β
- J =
Jacobian of the deformation gradient
- k =
strain-dependent permeability tensor
- k0 =
initial hydraulic permeability (mm/N s)
- M =
exponential strain-dependence coefficient in Holmes–Mow permeability
- MW =
molecular weight (Da)
- p =
fluid pressure (kPa)
- =
effective fluid pressure,
- p0 =
prescribed initial fluid pressure (kPa)
- R =
universal gas constant (8.31451 J/mol K)
- r0 =
initial radius of infusion cavity (mm)
- Tc50 =
time required for the solute concentration between two sources to be half of the prescribed solute concentration
- v =
Poisson's ratio
- V =
volume (mm3)
- Vd =
volume dispersed (ml)
- Vd:Vi =
mean distribution ratio
- Vi =
total volume infused (mm3)
- vα =
velocity of constituent, α (mm/s)
- w =
weight (kg)
Greek Symbols
- α =
general constituent in biphasic model
- β =
power-law exponent in Holmes–Mow permeability
- θ =
absolute temperature (K)
- ρα =
apparent density for the constituent (α), φα (kg/m3)
- =
true density of constituent, α (kg/m3)
- σe =
elastic solid stress in the porous matrix
- ϕ =
osmotic coefficient
- φα =
volume fraction of the constituent, α
Superscripts/Subscripts
- a =
solute
- d =
dispersed
- i =
`infused
- s =
solid
- w =
solvent
References
- [1]. Ostrom, Q. T. , Gittleman, H. , Xu, J. , Kromer, C. , Wolinsky, Y. , Kruchko, C. , and Barnholtz-Sloan, J. S. , 2016, “ CBTRUS Statistical Report: Primary Brain and Other Central Nervous System Tumors Diagnosed in the United States in 2009-2013,” Neuro-Oncology, 18(Suppl. 5), pp. v1–v75. 10.1093/neuonc/now207 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2]. Berger, M. S. , 1994, “ Malignant Astrocytomas: Surgical Aspects,” Semin. Oncol., 21(2), pp. 172–185.http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=PubMed&dopt=Citation&list_uids=8153663 [PubMed] [Google Scholar]
- [3]. Lesser, G. J. , and Grossman, S. , 1994, “ The Chemotherapy of High-Grade Astrocytomas,” Semin. Oncol., 21(2), pp. 220–235.http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=PubMed&dopt=Citation&list_uids=8153666 [PubMed] [Google Scholar]
- [4]. Shaw, E. J. , 2000, “ Central Nervous System Overview,” Clinical Radiation Oncology, Gunderson L. L., and Tepper J. E., eds., Churchill-Livingstone, Philadelphia, PA, pp. 314–354. [Google Scholar]
- [5]. Galanis, E. , and Bucker, J. , 2000, “ Chemotherapy for High-Grade Gliomas,” Br. J. Cancer, 82(8), pp. 1371–1380. 10.1054/bjoc.1999.1075 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6]. Grossman, S. A. , and Batara, J. F. , 2004, “ Current Management of Glioblastoma Multiforme,” Semin. Oncol., 31(5), pp. 635–644. 10.1053/j.seminoncol.2004.07.005 [DOI] [PubMed] [Google Scholar]
- [7]. Bart, J. , Groen, H. J. M. , Hendrikse, N. H. , van der Graaf, W. T. A. , Vaalburg, W. , and de Vries, E. G. E. , 2000, “ The Blood-Brain Barrier and Oncology: New Insights Into Function and Modulation,” Cancer Treat. Rev., 26(6), pp. 449–462. 10.1053/ctrv.2000.0194 [DOI] [PubMed] [Google Scholar]
- [8]. Kemper, E. M. , Boogerd, W. , Thuis, I. , Beijnen, J. H. , and van Tellingen, O. , 2004, “ Modulation of the Blood-Brain Barrier in Oncology: Therapeutic Opportunities for the Treatment of Brain Tumours?,” Cancer Treat. Rev., 30(5), pp. 415–423. 10.1016/j.ctrv.2004.04.001 [DOI] [PubMed] [Google Scholar]
- [9]. Ostrom, Q. T. , Gittleman, H. , Fulop, J. , Liu, M. , Blanda, R. , Kromer, C. , Wolinsky, Y. , Kruchko, C. , and Barnholtz-Sloan, J. S. , 2015, “ CBTRUS Statistical Report: Primary Brain and Central Nervous System Tumors Diagnosed in the United States in 2008–2012,” Neuro-Oncology, 17(Suppl. 4), pp. iv1–iv62. 10.1093/neuonc/nov189 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10]. Morrison, P. F. , Laske, D. W. , Bobo, H. , Oldfield, E. H. , and Dedrick, R. L. , 1994, “ High-Flow Microinfusion: Tissue Penetration and Pharmacodynamics,” Am. J. Physiol., 266(1 Pt. 2), pp. R292–R305. 10.1152/ajpregu.1994.266.1.R292 [DOI] [PubMed] [Google Scholar]
- [11]. Morrison, P. F. , Chen, M. Y. , Chadwick, R. S. , Lonser, R. R. , and Oldfield, E. H. , 1999, “ Focal Delivery During Direct Infusion to Brain: Role of Flow Rate, Catheter Diameter, and Tissue Mechanics,” Am. J. Physiol., 277(4), pp. R1218–R1229. 10.1152/ajpregu.1999.277.4.R1218 [DOI] [PubMed] [Google Scholar]
- [12]. Bobo, R. H. , Laske, D. W. , Akbasak, A. , Morrison, P. F. , Dedrick, R. L. , and Oldfield, E. H. , 1994, “ Convection-Enhanced Delivery of Macromolecules in the Brain,” Proc. Natl. Acad. Sci. USA, 91(6), pp. 2076–2080. 10.1073/pnas.91.6.2076 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13]. Laske, D. W. , Youle, R. J. , and Oldfield, E. H. , 1997, “ Tumor Regression With Regional Distribution of the Targeted Toxin TF-CRM107 in Patients With Malignant Brain Tumors,” Nat. Med., 3(12), pp. 1362–1368. 10.1038/nm1297-1362 [DOI] [PubMed] [Google Scholar]
- [14]. Vogelbaum, M. A. , and Aghi, M. K. , 2015, “ Convection-Enhanced Delivery for the Treatment of Glioblastoma,” Neuro-Oncology, 17(Suppl. 2), pp. ii3–ii8. 10.1093/neuonc/nou354 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15]. Vandergrift, W. A. , Patel, S. J. , Nicholas, J. S. , and Varma, A. K. , 2006, “ Convection-Enhanced Delivery of Immunotoxins and Radioisotopes for Treatment of Malignant Gliomas,” Neurosurg. Focus, 20(4), p. E13. 10.3171/foc.2006.20.4.8 [DOI] [PubMed] [Google Scholar]
- [16]. Patel, S. J. , Shapiro, W. R. , Laske, D. W. , Jensen, R. L. , Asher, A. L. , Wessels, B. W. , Carpenter, S. P. , and Shan, J. S. , 2005, “ Safety and Feasibility of Convection-Enhanced Delivery of Cotara for the Treatment of Malignant Glioma: Initial Experience in 51 Patients,” Neurosurgery, 56(6), pp. 1243–1253. 10.1227/01.NEU.0000159649.71890.30 [DOI] [PubMed] [Google Scholar]
- [17]. Kunwar, S. , 2003, “ Convection Enhanced Delivery of IL13-PE38QQR for Treatment of Recurrent Malignant Glioma: Presentation of Interim Findings From Ongoing Phase I Studies,” Acta Neurochir. Suppl., 88, pp. 105–111.https://www.ncbi.nlm.nih.gov/pubmed/14531568 [DOI] [PubMed] [Google Scholar]
- [18]. Debinski, W. , and Tatter, S. B. , 2009, “ Convection-Enhanced Delivery for the Treatment of Brain Tumors,” Expert Rev. Neurother., 9(10), pp. 1519–1527. 10.1586/ern.09.99 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19]. Kunwar, S. , Chang, S. , Westphal, M. , Vogelbaum, M. , Sampson, J. , Barnett, G. , Shaffrey, M. , Ram, Z. , Piepmeier, J. , Prados, M. , Croteau, D. , Pedain, C. , Leland, P. , Husain, S. R. , Joshi, B. H. , Puri, R. K. , and Group, P. S. , 2010, “ Phase III Randomized Trial of CED of IL13-PE38QQR versus Gliadel Wafers for Recurrent Glioblastoma,” Neuro Oncol., 12(8), pp. 871–881. 10.1093/neuonc/nop054 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20]. Sampson, J. H. , Archer, G. , Pedain, C. , Wembacher-Schroder, E. , Westphal, M. , Kunwar, S. , Vogelbaum, M. A. , Coan, A. , Herndon, J. E. , Raghavan, R. , Brady, M. L. , Reardon, D. A. , Friedman, A. H. , Friedman, H. S. , Rodriguez-Ponce, M. I. , Chang, S. M. , Mittermeyer, S. , Croteau, D. , Puri, R. K. , and Investigators, P. T. , 2010, “ Poor Drug Distribution as a Possible Explanation for the Results of the PRECISE Trial,” J. Neurosurg., 113(2), pp. 301–309. 10.3171/2009.11.JNS091052 [DOI] [PubMed] [Google Scholar]
- [21]. Brady, M. L. , Raghavan, R. , Singh, D. , Anand, P. J. , Fleisher, A. S. , Mata, J. , Broaddus, W. C. , and Olbricht, W. L. , 2014, “ In Vivo Performance of a Microfabricated Catheter for Intraparenchymal Delivery,” J. Neurosci. Methods, 229, pp. 76–83. 10.1016/j.jneumeth.2014.03.016 [DOI] [PubMed] [Google Scholar]
- [22]. Gill, T. , Barua, N. U. , Woolley, M. , Bienemann, A. S. , Johnson, D. E. , Sullivan, S. O. , Murray, G. , Fennelly, C. , Lewis, O. , Irving, C. , Wyatt, M. J. , Moore, P. , and Gill, S. S. , 2013, “ In Vitro and In Vivo Testing of a Novel Recessed-Step Catheter for Reflux-Free Convection-Enhanced Drug Delivery to the Brain,” J. Neurosci. Methods, 219(1), pp. 1–9. 10.1016/j.jneumeth.2013.06.008 [DOI] [PubMed] [Google Scholar]
- [23]. Krauze, M. T. , Saito, R. , Noble, C. , Tamas, M. , Bringas, J. , Park, J. W. , Berger, M. S. , and Bankiewicz, K. , 2005, “ Reflux-Free Cannula for Convection-Enhanced High-Speed Delivery of Therapeutic Agents,” J. Neurosurg., 103(5), pp. 923–929. 10.3171/jns.2005.103.5.0923 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24]. Vazquez, L. C. , Hagel, E. , Willenberg, B. J. , Dai, W. , Casanova, F. , Batich, C. D. , and Sarntinoranont, M. , 2012, “ Polymer-Coated Cannulas for the Reduction of Backflow During Intraparenchymal Infusions,” J. Mater. Sci. Mater. Med., 23(8), pp. 2037–2046. 10.1007/s10856-012-4652-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25]. Yin, D. , Forsayeth, J. , and Bankiewicz, K. S. , 2010, “ Optimized Cannula Design and Placement for Convection-Enhanced Delivery in Rat Striatum,” J. Neurosci. Methods, 187(1), pp. 46–51. 10.1016/j.jneumeth.2009.12.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26]. DeAngelis, L. M. , 2001, “ Brain Tumors,” N. Engl. J. Med., 344(2), pp. 114–123. 10.1056/NEJM200101113440207 [DOI] [PubMed] [Google Scholar]
- [27]. Vogelbaum, M. A. , 2014, “ A Pilot Trial of Intraparenchymally-Administered Topotecan Using Convection-Enhanced Delivery (CED) in Patients With Suspected Recurrent/Progressive WHO Grade III or IV (High Grade) Glioma Requiring Stereotactic Biopsy,” National Library of Medicine, Bethesda, MD, Document No. NCT02278510.
- [28]. Barua, N. U. , Hopkins, K. , Woolley, M. , O'Sullivan, K. , Harrison, R. , Edwards, R. J. , Bienemann, A. , Wyatt, M. J. , Arshad, A. , and Gill, S. , 2016, “ A Novel Implantable Catheter System With Transcutaneous Port for Intermittent Convection-Enhanced Delivery of Carboplatin for Recurrent Glioblastoma,” Drug Delivery, 23(1), pp. 17–173. 10.3109/10717544.2014.908248 [DOI] [PubMed] [Google Scholar]
- [29]. Elenes, E. Y. , and Rylander, C. G. , 2017, “ Maximizing Local Access to Therapeutic Deliveries in Glioblastoma—Part II: Arborizing Catheter for Convection-Enhanced Delivery in Tissue Phantoms,” Glioblastoma, De Vleeschouwer S., ed., Codon Publications, Brisbane, QLD. [PubMed] [Google Scholar]
- [30]. Mauck, R. L. , Hung, C. T. , and Ateshian, G. A. , 2003, “ Modeling of Neutral Solute Transport in a Dynamically Loaded Porous Permeable Gel: Implications for Articular Cartilage Biosynthesis and Tissue Engineering,” ASME J. Biomech. Eng., 125(5), pp. 602–614. 10.1115/1.1611512 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31]. Ateshian, G. A. , Likhitpanichkul, M. , and Hung, C. T. , 2006, “ A Mixture Theory Analysis for Passive Transport in Osmotic Loading of Cells,” J. Biomech., 39(3), pp. 464–475. 10.1016/j.jbiomech.2004.12.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32]. Ateshian, G. A. , Albro, M. B. , Maas, S. , and Weiss, J. A. , 2011, “ Finite Element Implementation of Mechanochemical Phenomena in Neutral Deformable Porous Media Under Finite Deformation,” ASME J. Biomech. Eng., 133(8), p. 081005. 10.1115/1.4004810 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33]. Maas, S. , Rawlins, D. , Weiss, J. A. , and Ateshian, G. A. , 2015, “ FEBio: Finite Elements for Biomechanics Theory Manual,” accessed Feb. 27, 2019, http://mrl.sci.utah.edu/software/febio
- [34]. Gu, W. Y. , Lai, W. M. , and Mow, V. C. , 1998, “ A Mixture Theory for Charged-Hydrated Soft Tissues Containing Multi-Electrolytes: Passive Transport and Swelling Behaviors,” ASME J. Biomech. Eng., 120(2), pp. 169–180. 10.1115/1.2798299 [DOI] [PubMed] [Google Scholar]
- [35]. Normand, V. , Lootens, D. L. , Amici, E. , Plucknett, K. P. , and Aymard, P. , 2000, “ New Insights Into Agarose Gel Mechanical Properties,” Biomacromolecules, 1(4), pp. 730–738. 10.1021/bm005583j [DOI] [PubMed] [Google Scholar]
- [36]. Pluen, A. , Netti, P. A. , Jain, R. K. , and Berk, D. A. , 1999, “ Diffusion of Macromolecules in Agarose Gels: Comparison of Linear and Globular Configurations,” Biophys. J., 77(1), pp. 542–552. 10.1016/S0006-3495(99)76911-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37]. Holmes, M. H. , and Mow, V. C. , 1990, “ The Nonlinear Characteristics of Soft Gels and Hydrated Connective Tissues in Ultrafiltration,” J. Biomech., 23(11), pp. 1145–1156. 10.1016/0021-9290(90)90007-P [DOI] [PubMed] [Google Scholar]
- [38]. Lai, W. M. , and Mow, V. C. , 1980, “ Drag-Induced Compression of Articular Cartilage During a Permeation Experiment,” Biorheology, 17(1–2), pp. 111–123. 10.3233/BIR-1980-171-213 [DOI] [PubMed] [Google Scholar]
- [39]. Garcia, J. J. , and Smith, J. H. , 2009, “ A Biphasic Hyperelastic Model for the Analysis of Fluid and Mass Transport in Brain Tissue,” Ann. Biomed. Eng., 37(2), pp. 375–386. 10.1007/s10439-008-9610-0 [DOI] [PubMed] [Google Scholar]
- [40]. Chen, X. , and Sarntinoranont, M. , 2007, “ Biphasic Finite Element Model of Solute Transport for Direct Infusion Into Nervous Tissue,” Ann. Biomed. Eng., 35(12), pp. 2145–2158. 10.1007/s10439-007-9371-1 [DOI] [PubMed] [Google Scholar]
- [41]. Sobey, I. , and Wirth, B. , 2006, “ Effect of Non-Linear Permeability in a Spherically Symmetric Model of Hydrocephalus,” Math. Med. Biol., 23(4), pp. 339–361. 10.1093/imammb/dql015 [DOI] [PubMed] [Google Scholar]
- [42]. Cheng, S. , and Bilston, L. E. , 2007, “ Unconfined Compression of White Matter,” J. Biomech., 40(1), pp. 117–124. 10.1016/j.jbiomech.2005.11.004 [DOI] [PubMed] [Google Scholar]
- [43]. Muralidharan, P. , 2006, “ Finite Deformation Biphasic Material Characterization and Modeling of Agarose Gel for Functional Tissue Engineering Applications,” Master's thesis, University of Cincinnati, Cincinnati, OH. [Google Scholar]
- [44]. Tao, L. , and Nicholson, C. , 1996, “ Diffusion of Albumins in Rat Cortical Slices and Relevance to Volume Transmission,” Neuroscience, 75(3), pp. 839–847. 10.1016/0306-4522(96)00303-X [DOI] [PubMed] [Google Scholar]
- [45]. Rausch, M. K. , and Humphrey, J. D. , 2017, “ A Computational Model of the Biochemomechanics of an Evolving Occlusive Thrombus,” J. Elasticity, 129(1–2), pp. 125–144. 10.1007/s10659-017-9626-5 [DOI] [Google Scholar]
- [46]. Chen, M. Y. , Lonser, R. R. , Morrison, P. F. , Governale, L. S. , and Oldfield, E. H. , 1999, “ Variables Affecting Convection-Enhanced Delivery to the Striatum: A Systematic Examination of Rate of Infusion, Cannula Size, Infusate Concentration, and Tissue–Cannula Sealing Time,” J. Neurosurg., 90(2), pp. 315–320. 10.3171/jns.1999.90.2.0315 [DOI] [PubMed] [Google Scholar]
- [47]. Netti, P. A. , and Travascio, F. , 2003, “ Coupled Macromolecular Transport and Gel Mechanics: Poroviscoelastic Approach,” Bioeng. Food Nat. Prod., 49(6), pp. 1580–1596. 10.1002/aic.690490621 [DOI] [Google Scholar]
- [48]. Sampson, J. H. , Akabani, G. , Archer, G. E. , Bigner, D. D. , Berger, M. S. , Friedman, A. H. , Friedman, H. S. , Herndon, J. E., II , Kunwar, S. , Marcus, S. , McLendon, R. E. , Paolino, A. , Penne, K. , Provenzale, J. , Quinn, J. , Reardon, D. A. , Rich, J. , Stenzel, T. , Tourt-Uhlig, S. , Wikstrand, C. , Wong, T. , Williams, R. , Yuan, F. , Zalutsky, M. R. , and Pastan, I. , 2003, “ Progress Report of a Phase I Study of the Intracerebral Microinfusion of a Recombinant Chimeric Protein Composed of Transforming Growth Factor (TGF)-α and a Mutated Form of the Pseudomonas Exotoxin Termed PE-38 (TP-38) for the Treatment of Malignant Brain Tumors,” J. Neurooncol., 65(1), pp. 27–35. 10.1023/A:1026290315809 [DOI] [PubMed] [Google Scholar]
- [49]. Rand, R. W. , Kreitman, R. J. , Patronas, N. , Varricchio, F. , Pastan, I. , and Puri, R. K. , 2000, “ Intratumoral Administration of Recombinant Circularly Permuted Interleukin-4-Pseudonomas Exotoxin in Patients With High-Grade Glioma,” Clin. Cancer Res., 6(6), pp. 2157–2165.https://www.ncbi.nlm.nih.gov/pubmed/10873064 [PubMed] [Google Scholar]
- [50]. Lonser, R. R. , Walbridge, S. , Garmestani, K. , Butman, J. A. , Walters, H. A. , Vortmeyer, A. O. , Morrison, P. F. , Brechbiel, M. W. , and Oldfield, E. H. , 2002, “ Successful and Safe Perfusion of the Primate Brainstem: In Vivo Magnetic Resonance Imaging of Macromolecular Distribution During Infusion,” J. Neurosurg., 97(4), pp. 905–913. 10.3171/jns.2002.97.4.0905 [DOI] [PubMed] [Google Scholar]
- [51]. Lonser, R. R. , Sarntinoranont, M. , Morrison, P. F. , and Oldfield, E. H. , 2015, “ Convection-Enhanced Delivery to the Central Nervous System,” J. Neurosurg., 122(3), pp. 697–706. 10.3171/2014.10.JNS14229 [DOI] [PubMed] [Google Scholar]
- [52]. Chittiboina, P. , Heiss, J. D. , Warren, K. E. , and Lonser, R. R. , 2014, “ Magnetic Resonance Imaging Properties of Convective Delivery in Diffuse Intrinsic Pontine Gliomas,” J. Neurosurg. Pediatr., 13(3), pp. 276–282. 10.3171/2013.11.PEDS136 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53]. Smith, J. H. , and Garcia, J. J. , 2011, “ A Nonlinear Biphasic Model of Flow-Controlled Infusions in Brain: Mass Transport Analyses,” J. Biomech., 44(3), pp. 524–531. 10.1016/j.jbiomech.2010.09.010 [DOI] [PubMed] [Google Scholar]
- [54]. Polivka, J., Jr. , Polivka, J. , Holubec, L. , Kubikova, T. , Priban, V. , Hes, O. , Pivovarcikova, K. , and Treskova, I. , 2017, “ Advances in Experimental Targeted Therapy and Immunotherapy for Patients With Glioblastoma Multiforme,” Anticancer Res., 37(1), pp. 21–33.http://ar.iiarjournals.org/content/37/1/21.full [DOI] [PubMed] [Google Scholar]
- [55]. Touat, M. , Idbaih, A. , Sanson, M. , and Ligon, K. L. , 2017, “ Glioblastoma Targeted Therapy: Updated Approaches From Recent Biological Insights,” Ann. Oncol., 28(7), pp. 1457–1472. 10.1093/annonc/mdx106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56]. Xu, Y. Y. , Gao, P. , Sun, Y. , and Duan, Y. R. , 2015, “ Development of Targeted Therapies in Treatment of Glioblastoma,” Cancer Biol. Med., 12(3), pp. 223–237. 10.7497/j.issn.2095-3941.2015.0020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [57]. Chen, Z. J. , Broaddus, W. C. , Viswanathan, R. R. , Raghavan, R. , and Gillies, G. T. , 2002, “ Intraparenchymal Drug Delivery Via Positive-Pressure Infusion: Experimental and Modeling Studies of Poroelasticity in Brain Phantom Gels,” IEEE Trans. Biomed. Eng., 49(2), pp. 85–96. 10.1109/10.979348 [DOI] [PubMed] [Google Scholar]
- [58]. Chen, Z. J. , Gillies, G. T. , Broaddus, W. C. , Prabhu, S. S. , Fillmore, H. , Mitchell, R. M. , Corwin, F. D. , and Fatouros, P. P. , 2004, “ A Realistic Brain Tissue Phantom for Intraparenchymal Infusion Studies,” J. Neurosurg., 101(2), pp. 314–322. 10.3171/jns.2004.101.2.0314 [DOI] [PubMed] [Google Scholar]
- [59]. Kaczmarek, M. , Subramaniam, R. P. , and Neff, S. R. , 1997, “ The Hydromechanics of Hydrocephalus: Steady-State Solutions for Cylindrical Geometry,” Bull. Math. Biol., 59(2), pp. 295–323. 10.1007/BF02462005 [DOI] [PubMed] [Google Scholar]
- [60]. Stewart, D. C. , Rubiano, A. , Dyson, K. , and Simmons, C. S. , 2017, “ Mechanical Characterization of Human Brain Tumors From Patients and Comparison to Potential Surgical Phantoms,” PLoS One, 12(6), p. e0177561. 10.1371/journal.pone.0177561 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [61]. Raghavan, R. , Brady, M. L. , Rodriguez-Ponce, M. I. , Hartlep, A. , Pedain, C. , and Sampson, J. H. , 2006, “ Convection-Enhanced Delivery of Therapeutics for Brain Disease, and Its Optimization,” Neurosurg. Focus, 20(4), p. E12. 10.3171/foc.2006.20.4.7 [DOI] [PubMed] [Google Scholar]
- [62]. Smith, J. H. , and Garcia, J. J. , 2009, “ A Nonlinear Biphasic Model of Flow-Controlled Infusion in Brain: Fluid Transport and Tissue Deformation Analyses,” J. Biomech., 42(13), pp. 2017–2025. 10.1016/j.jbiomech.2009.06.014 [DOI] [PubMed] [Google Scholar]


