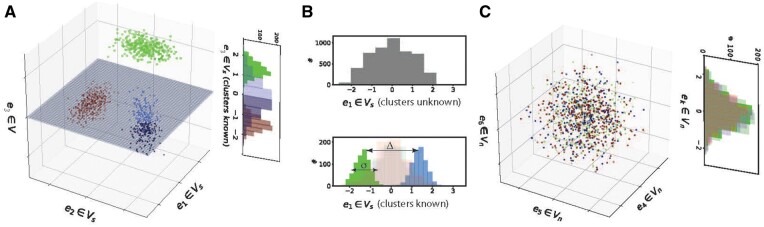
Fig. 2.

For K clusters with multimodal subspaces $V_s^{lm}$ with $l,m\in \{1,\dots ,K\}$, we consider the limit as each $V_s^{lm}$ has minimal dimension (=1) and are non-intersecting. (A) shows a Gaussian example of a collection of one-dimensional pairwise informative subspaces, which are uninformative for clusters $\ne l,m$. Here, e₁ is multimodal in the blue and green clusters, but not red, e₂ is multimodal in the red and blue clusters, but not green, and e₃ is multimodal in the red and green clusters, but not blue. (B) Despite containing multimodal signature, non-intersecting pairwise informative subspaces $V_s^{lm}$ can corrupt marginal distributions to hide separability (top). Same data with points colored by cluster, where separation of means is denoted by Δ, and the variance of distributions in their informative dimensions is given by σ. (bottom). (C) shows dimensions that are uninformative for all clusters