A novel transcriptional risk score for risk prediction of complex human diseases

Abstract

Recently polygenetic risk score (PRS) has been successfully used in risk prediction of complex human diseases. Many studies incorporated internal information such as effect size distribution, or external information such as linkage disequilibrium, functional annotation, and pleiotropy among multiple diseases, to optimize the performance of PRS. In order to leverage on multi-omics datasets, we developed a novel flexible transcriptional risk score (TRS), in which mRNA expression levels were imputed and weighted for risk prediction. In simulation studies, we demonstrated that single-tissue TRS has greater prediction power than LDpred, especially when there is a large effect of gene expression on the phenotype. Multi-tissue TRS improves prediction accuracy when there are multiple tissues with independent contributions to disease risk. We applied our method to complex traits including Crohn’s disease, type 2 diabetes, etc.. Single-tissue TRS method outperformed LDpred and AnnoPred across the tested traits. The performance of multi-tissue TRS is trait-dependent. Moreover, our method can easily incorporate information from epigenomic and proteomic data upon availability of reference datasets.

1. INTRODUCTION

Genome-wide association studies (GWAS) have been successful in identifying tens of thousands of genetic variants associated with human complex traits and diseases. As large-scale GWAS analyses of many complex traits become available, there is an increasing interest in genetic risk prediction. Recently, polygenetic risk score (PRS), a weighted sum of risk alleles, is frequently employed for risk prediction of complex traits with polygenic genetic architecture, however, the predictive power is usually limited^1–3. The prediction accuracy of PRS falls short of what is expected from the theoretical PRS due to statistical variation in the selection of SNPs and estimation of coefficients when constructing PRS. Improvement on the prediction performance requires a huge sample size in GWAS¹. The explained variance and the predictive value of PRS are low in general population, thus it is still insufficient for clinical utility and interpretation^2,3.

Prediction accuracy can be improved by re-estimation of the weight parameters in PRS. To optimize PRS, LDpred⁴ and lassosum⁵ incorporated the linkage disequilibrium (LD) information estimated from a reference panel. JAMpred⁶ proposed a two-step approach to adjust for local LD and long-range LD, which had similar performance to LDpred and lassosum for most traits while provided better prediction accuracy for type 1 diabetes (T1D). Shi et al. (2016) labeled SNPs with “high prior” and “low prior” based on functional annotations including expression quantitative trait loci (eQTLs), methylation QTLs (meQTLs), and cis-regulatory elements (CREs), and adjusted the marginal effect size estimation of SNPs to alleviate winner’s curse⁷. AnnoPred leveraged multiple types of genomic and epigenomic functional annotations⁸. PleioPred⁹, SMTpred¹⁰, MATG¹¹, and CTPR¹² utilized genetic correlations among multiple traits/diseases to adjust the effect size estimation. Similarly, multi-polygenic score (MPS) from multiple GWASs was directly constructed to increase predictive power¹³. In addition, re-estimating effect size distributions via Bayesian approaches improves the prediction accuracy of PRS. Typically, the observed effect sizes were weighted by the local true discovery rate¹⁴, or corrected using the Tweedie’s formula first, and then weighted by the local true discovery rate¹⁵. The effect sizes were modeled using a normal-mixture model and a likelihood-based approach was developed to estimate effect-size distributions by considering external LD information and the probability of SNPs in different mixture components¹⁶. SBayesR assigned a prior of finite mixture of normal distributions on the linear coefficients of multiple regression to infer the posterior estimation¹⁷. PRS-CS considered a high dimensional Bayesian regression framework and assigned continuous shrinkage priors on the effect sizes, which enabled block update of effect sizes and allowed for modeling of local LD patterns¹⁸. EB-PRS utilized a spike-and-slab prior to model the effect sizes across all markers and then estimated the posterior mean of the effect sizes by minimizing the Bayes risk¹⁹.

Human traits or diseases are results of interplay between environmental and genetic factors, such as genomic, transcriptomic, epigenomic, and proteomic variations^20,21. With the advance of high-throughput biotechnologies, multi-omics data (genome, epigenome, transcriptome, proteome, and metabolome) has become popular in biological and clinical studies²². Increasing amount of multi-omics data provides us an unprecedented opportunity to integrate information beyond that from any single data type. Several methods have been developed to combine multiple data types, such as directly using metabolites as features to guide prediction²³, and integrating GWASs and eQTLs with transcriptional data to obtain risk scores²⁴. Previous studies have shown that data integration may improve the predictive power of human diseases^23,24. However, these studies relied on the availability of individual-level omics data. Gusev et al. (2018) constructed a gene-based PRS as the sum of predicted gene expression weighted by signed association statistics from transcriptome-wide association studies (TWAS) and assessed the marginal and joint effects of gene-based PRS from multiple tissues on risk prediction of Schizophrenia²⁵. They only considered the effects from several specific tissues, and potentially valuable information from other available tissues were ignored, which may lead to selection bias in prediction. In addition, it is unclear whether gene-based PRS improves predictive power beyond SNP-based PRS. Zhao et al. (2019) constructed a gene-based PRS based on imputed gene expression, which achieved additional predictive power compared to the traditional PRS, while the weights in gene-based PRS were directly estimated from each imputed gene expression and phenotype. They assessed the performance of gene-based PRS in a single tissue²⁶.

In this work, we propose a flexible analytical form of transcriptional risk scores (TRS) assuming that individual-level gene expression is not available. It consists of two steps. In the first step, gene imputation was performed using PrediXcan²⁷. In the second step, weights of the imputed gene expression were estimated using S-PrediXcan²⁸. We systematically evaluated the performance of the proposed method in single tissue and multiple tissues in the 48 GTEx (v7) reference panels. In simulation studies, we assessed the performance of combining LDpred PRS with single-tissue TRS (STRS) or multi-tissue TRS (MTRS). We demonstrated that STRS improved the prediction accuracy of LDpred, especially when there is a large effect of gene expression on the phenotype. MTRS improved prediction accuracy when there are multiple tissues with independent contributions to disease risk. When applied to seven traits in the Wellcome Trust Case Control Consortium (WTCCC) datasets and two traits in meta-GWAS studies, the STRS method achieved greater predictive power than LDpred and AnnoPred alone. The performances of MTRS depended on the trait of interest. Furthermore, our method can be easily extended to incorporate epigenomic and proteomic data when reference data becomes available.

2. METHODS

2.1. WTCCC dataset

We used the WTCCC datasets²⁹ to evaluate the model performance. In genotype data, we excluded individuals with genetic relatedness coefficient greater than 0.05, and variants with missing rate greater than 1%⁸. After filtering, we had 15,918 individuals and 393,273 variants in the analysis. The WTCCC study includes seven diseases, including bipolar disorder (BD), coronary artery disease (CAD), Crohn’ disease (CD), hypertension (HT), rheumatoid arthritis (RA), T1D, and type 2 diabetes (T2D) (see Supplementary Table 1 for details).

2.2. GWAS summary statistics

We obtained independent GWAS summary statistics and individual level genotype and phenotype information for training and testing for T2D and CD. Thus, TRSs were constructed with the GWAS summary statistics, and the performance of STRS and MTRS in T2D and CD were further evaluated in independent test cohorts. For T2D, we obtained the summary statistics from the Diabetes Genetics Replication and Meta-analysis consortium, including 56,862 cases and 12,171 controls genotyped on 2,400,624 SNPs³⁰. Note that the WTCCC samples were included in the meta-analysis, and we used a separate cohort, the Northwestern NUgene Project³¹, including 629 cases and 710 controls genotyped on 478,237 SNPs, as the test data. For CD, we obtained the summary statistics from the International Inflammatory Bowel Disease Genetics Consortium, including 15,056 cases and 6,333 controls genotyped on 871,743 variants³². We tested our model on the WTCCC CD samples (1,696 cases and 2,876 controls)²⁹. Individuals in the WTCCC study were removed in the GWAS meta-analysis to avoid overlapping samples between the training and test datasets.

2.3. Genotype imputation

The SHAPEIT program³³ was used to generate the phased haplotypes, and MiniMac3³⁴ was used to impute genotypes in the WTCCC dataset and Northwestern Nugene Project dataset. The 1000 Genomes phase3 v5 data³⁵ (http://csg.sph.umich.edu/abecasis/MaCH/download/1000G.Phase3.v5.html) was used as the reference panel, with approximately 41 million imputed variants. We retained all variants with an imputation R² > 0.8²⁷, yielding about 7 million variants.

2.4. Transcriptional risk scores

Suppose we have a sample of n individuals. Let Y be an n-dimensional vector of the phenotype and X_l be the vector of allele dosage for SNP l, on the n individuals. $T_g=\sum _{l\in {model}_g}{w}_{lg}{X}_l$ is the vector of imputed gene expression for gene g, where w_lg is the weight of SNP l derived from GTEx (v7) reference panels when imputing gene g using the PrediXcan software. The marginal effects of the SNPs and imputed gene expressions were obtained by regressing the phenotype vector Y on X_l and T_g separately:

$$Y={\alpha }_1+X_l{\beta }_l+\epsilon$$ (1)

$$Y={\alpha }_2+T_g{\gamma }_g+\tau$$ (2)

where β_l is the effect size of SNP l, γg is the effect size of the imputed gene expression of gene g, α₁ and α₂ are intercepts, ε and τ are error terms. ${\widehat{\beta }}_l$ and ${\widehat{\gamma }}_g$ are the corresponding estimators. Suppose X is the n × m dosage matrix, where m is the number of SNPs selected in the imputation of gene $g.\widehat{{\Gamma }_g}$ is the sample variance-covariance matrix of X, which is estimated from a reference panel. In particular, the l-th diagonal element ${\widehat{\sigma }}_l^2$ is the estimated variance of SNP l, estimated by ${\widehat{\sigma }}_l^2=2p_l\left(1-p_l\right)$, where p_l is the minor allele frequency of SNP l in the reference panel. The estimated variance of the imputed gene expression T_g is ${\widehat{\sigma }}_g^2=\widehat{var}\left(T_g\right)=W_g^{\text{'}}\widehat{{\Gamma }_g}{W}_g$ where $W_g={(w_{1g},\cdots \cdots ,w_{mg})}^{\text{'}}$. The estimation of γg can be derived from GWAS summary statistics (see Appendix A of Supporting Information):

$${\widehat{\gamma }}_g=\frac{\sum _{l\in {model}_g}{w}_{lg}\widehat{{\beta }_l}{\widehat{\sigma }}_l^2}{{\widehat{\sigma }}_g^2}$$ (3)

The form of TRS, a weighted sum of imputed gene expression, was inspired by the form of PRS. Suppose that the effect of a variant on the phenotype is mediated through gene expression. We take the imputed value of genetically regulated expression (GRE) as a surrogate for gene expression, and estimate the corresponding effect size. Under the linear model assumption, TRS has a similar form as PRS, expressed as:

$$TRS={\sum }_g{T}_g{\widehat{\gamma }}_g={\sum }_g\left(\left({\sum }_{l\in {model}_g}{w}_{lg}{X}_l\right)\left(\frac{\sum _{l\in {model}_g}{w}_{lg}\widehat{{\beta }_l}{\widehat{\sigma }}_l^2}{{\widehat{\sigma }}_g^2}\right)\right)$$ (4)

In this study, gene imputation was performed for each of the 48 tissues in the GTEx (v7) reference panels using PrediXcan²⁷. S-PrediXcan²⁸ was used to estimate effect size of each imputed gene expression. Besides the weight parameters, the selection of genes in the construction of TRS formula may be challenging, because including genes with a stringent p-value threshold (e.g., p <5 ×10⁻⁶) may ignore valuable information from a larger gene set. Here, we included all imputable genes in TRS. TRS is then combined with PRS to train the predictors. For STRS, we fit a logistic model on the constructed TRS adjusting for the effects of LDpred or AnnoPred PRS. In detail, we first calculated TRS in each tissue, and then picked a tissue with the best predictive accuracy in the training dataset. In another word, single-tissue refers to the TRS constructed from the tissue with the best performance in the training set. For evaluation, the TRS from the selected tissue was applied to the test dataset. We implemented this procedure in 10-fold cross-validation, where the area under the receiver operating characteristic curve (AUC) was calculated in each test fold. The overall AUC is the average of the ten test AUCs.

For multiple tissues, we calculated TRS for each tissue, and then conducted least absolute shrinkage and selection operator-penalized regressions (LASSO) with 10-fold cross-validation to select features that have the criteria giving minimum mean cross-validated error³⁶, adjusting for the effects of LDpred or AnnoPred PRS. The analysis was performed using an R package ‘glmnet’.

2.5. Comparison with LDpred and AnnoPred

To benchmark the performance of TRS, we applied LDpred and AnnoPred to the WTCCC datasets and the meta-GWAS datasets. In LDpred, the subjects of European ancestry from 1000 Genomes were used as the LD reference panel. The tuning parameters, the LD radius and the fraction of causal variants, were run with default setting. AnnoPred was implemented with various annotations, including baseline, GenoCanyon, and GenoSkyline annotations, as previously described⁸.

2.6. Cross-validation in the WTCCC dataset

We divided the individual level genotype and phenotype dataset into ten folds of equal sizes using the function ‘createFolds’ in the R package ‘caret’. For each trait, we took 9 folds as the training data to estimate the effect size of each SNP and calculate LDpred PRS, AnnoPred PRS, and TRSs of 48 tissues. The training data was also used for parameter tuning in PRS and parameter estimation in STRS and MTRS. The predictors were evaluated in the leave-out samples. We repeated the process 10 times. The average AUC from the 10 repeats was used to quantify the model performance.

2.7. Method evaluation in the meta-GWAS applications

GWAS summary statistics in the training cohort were used to calculate LDpred PRS, AnnoPred PRS, and TRSs of 48 tissues. We also performed 10-fold cross- validation in the test cohort. Nine folds were used for parameter tuning in PRS and parameter estimation in STRS and MTRS. The remaining samples were used for testing. AUC was calculated in each test fold and the average AUC was used to evaluate model performance. The bootstrap paired Z test was used to compare the prediction accuracy of STRS or MTRS with that of LDpred or AnnoPred based on 100 stratified bootstrap replicates. The test statistics was defined as $Z=\frac{{AUC}_1-{AUC}_2}{sd({AUC}_1-{AUC}_2)}$, where AUC₁ and AUC₂ are the observed AUCs of two methods for comparison, and (AUC₁ − AUC₂) is computed with 100 stratified bootstrap replicates. In detail, we first resampled the same number of cases and controls as in the original data with replacement in each stratified bootstrap replicate and then computed the resampled AUCs and their difference. We repeated the process 100 times and computed the standard deviation of the AUC difference. As the test statistics approximately followed a normal distribution, one-tailed p-value was calculated accordingly. The analysis was performed using an R package ‘pROC’³⁷.

2.8. Simulation settings

We conducted simulation studies to evaluate the performance of STRS and MTRS. We simulated trait values based on the SNP genotypes on chromosome 1 in the WTCCC dataset, including 341,682 SNPs genotyped in 4,825 individuals. For simplification, we focused on imputable gene expression values in three tissues, including 597 genes in whole blood, 450 genes in pancreas, and 743 genes in subcutaneous adipose. Phenotypes were generated by:

$$log\frac{P(y=1|x)}{p(y=0|x)}=\sum _{l\in C}{\beta }_l{x}_l+\sum _{g_1\in G_1}{\gamma }_{g_1}\left(t_{g_1}+{\epsilon }_1\right)+\sum _{g_2\in G_2}{\gamma }_{g_2}\left(t_{g_2}+{\epsilon }_2\right)$$ (5)

where C is the set of causal variants, x_l is the standardized genotype, β_l~ $N\left(0,{\sigma }_1^2\right);G_1$ is the set of causal genes in whole blood, t_g1 is the standardized imputed gene expression of g₂ in whole blood, γg₁~ $N\left(0,{\sigma }_2^2\right);G_2$ is the set of causal genes in pancreas, t_g2 is the standardized imputed gene expression of g₂ in pancreas, γg₂~ $N\left(0,{\sigma }_3^2\right);{\gamma }_{g_1}$ and γ_g2 are independently sampled; ε₂~ $N\left(0,{\sigma }_4^2\right);{\epsilon }_2~$ $N\left(0,{\sigma }_5^2\right);{\epsilon }_1$ and ε₂ are independent.

Causal variants were selected as follows: 1) For a pair of SNPs with LD greater than 0.1 and with distance less than 500 kb⁷, we randomly removed one of the SNPs. 3,298 variants were retained after this step. 2) We randomly selected 300 variants from the pruned subset as causal variants. Casual genes were generated to reflect different levels of tissue specificity on the trait. We considered two scenarios. In scenario I, only genes in whole blood affect the trait values. Note that the gene set G₂ is empty in this scenario. Two hundred genes in whole blood were randomly selected as causal genes. We set σ₁ = 0.08, 0.10, 0.12 and σ₂= 0.15, 0.175, 0.20 to mimic the effects of variants and gene expression on the phenotype in the WTCCC dataset. σ₄ was set at 2 so that the variance explained by imputed gene expression was comparable to that reported in a previous study²⁷. In scenario II, genes in both whole blood and pancreas affect the trait values. We randomly selected 100 genes from whole blood and 100 genes from pancreas as casual genes and there were no overlapping genes from these two tissues. We set σ₁ = 0.1, σ₂ = σ₃= 0.15, 0.175, 0.20, and σ₄ = σ₅ = 2.

The average AUC from 10-fold cross-validation was used to evaluate the improvement in prediction accuracy. The standard error of the average AUC and p-value of the bootstrap test for comparing the performance of LDpred and the addition of STRS or MTRS with LDpred PRS were obtained using 100 stratified bootstrap replicates.

3. RESULTS

3.1. Simulation results

We performed simulations to evaluate the performance of TRS in single tissue and multiple tissues under different parameter settings, and the results were compared to LDpred. In scenario I where all the causal genes are from a single tissue, STRS showed consistent and significant improvement in prediction accuracy across all settings (Figure 1). For both TRS and LDpred, as we expected, the prediction accuracy increased as the effect sizes of variants increased under different settings, and the pattern was the same for gene expression. We also noticed that the extent of improvement of STRS over LDpred increased with larger standard deviation of the effect size of gene expression. The performance of MTRS was very similar to that of LDpred and the difference in AUC was not significant. When the trait has high tissue specificity, MTRS does not provide advantage compared to STRS, and its performance could be hampered by incorporating transcriptome information from irrelevant tissues. In scenario II where causal genes are distributed in two tissues, both STRS and MTRS significantly improved the prediction accuracy in all settings (Figure 2). As we expected, the extent of improvement from MTRS was larger than that from STRS, implicating that when multiple tissues contribute to disease risk, MTRS could leverage complementary information from all relevant tissues to improve prediction accuracy. In summary, the simulation results demonstrated that the TRS method improves risk prediction when heritability can be partially attributed to eQTLs, which is not uncommon in complex traits^25,26. Moreover, the improvement of TRS is larger when eQTLs explain more heritability through genetically regulated gene expression. When there are multiple tissues with independent contributions to disease risk, MTRS could provide additional improvement in predictive power.

Figure 1.

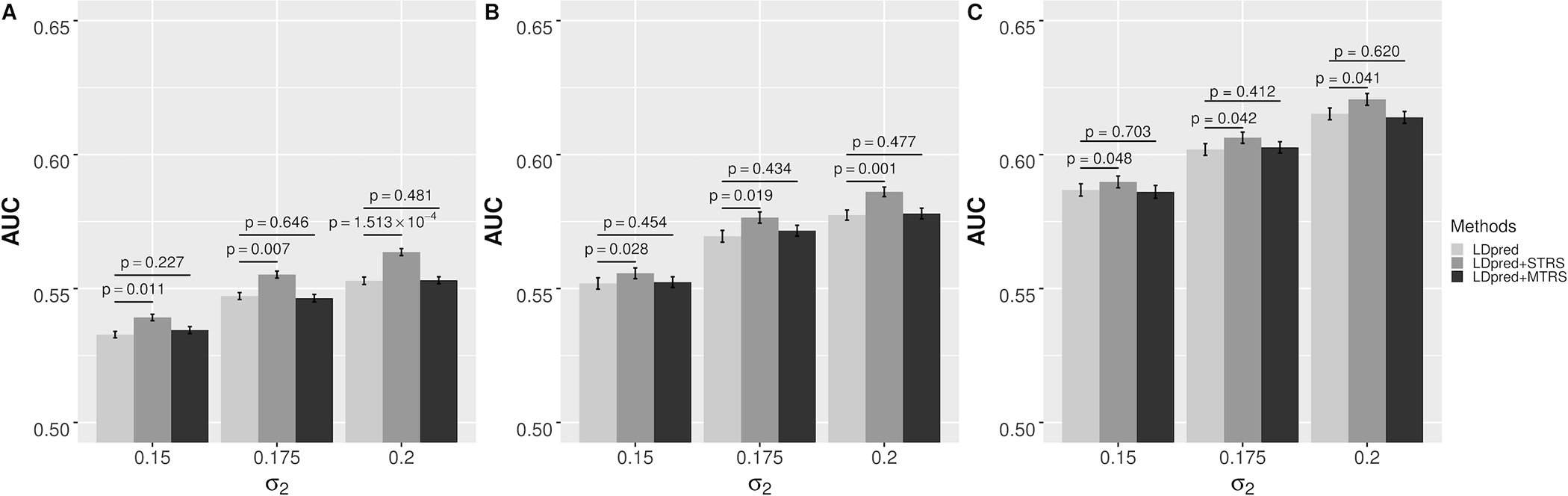
AUCs of different risk prediction methods in simulation scenario I that all causal genes are from a single tissue: (a) σ₁ = 0.08; (b) σ₁ = 0.10; (c) σ₁ = 0.12. The error bars indicate the standard error of prediction accuracy across 100 stratified bootstrap replicates. p-value is based on the bootstrap test of comparing LDpred with STRS or MTRS across 100 stratified bootstrap replicates.

Figure 2.

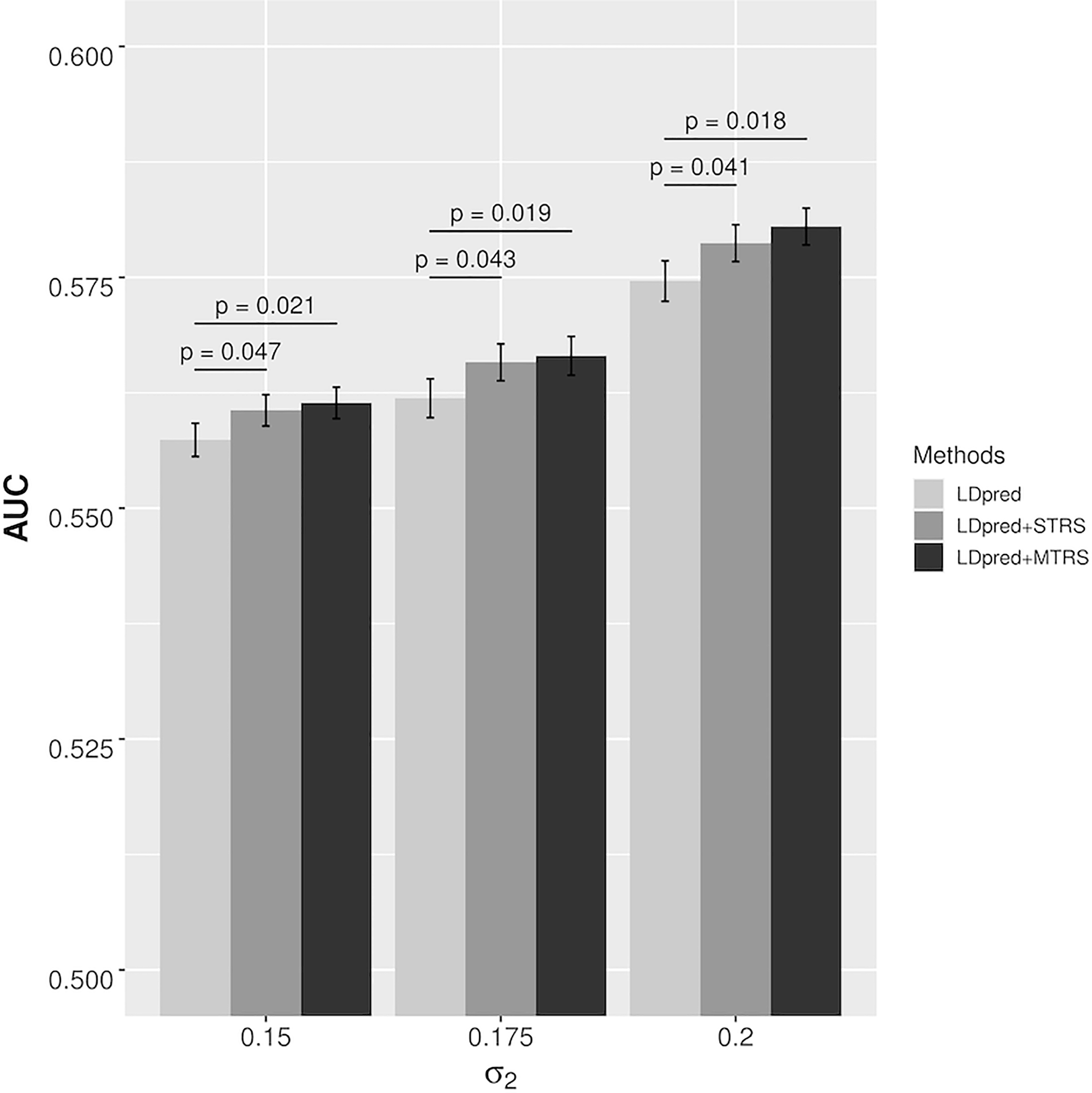
AUCs of different risk prediction methods in simulation scenario II that all causal genes are from two tissues. The error bars indicate the standard error of prediction accuracy across 100 stratified bootstrap replicates. p-value is based on the bootstrap test of comparing LDpred with STRS or MTRS across 100 stratified bootstrap replicates.

3.2. Cross-validation in the WTCCC dataset

To illustrate the improvement in risk prediction in real datasets, we applied TRS in single tissue and multiple tissues to seven traits in the WTCCC datasets using 10-fold cross-validation. LDpred and AnnoPred were used to benchmark the performance of TRS. The AUCs of all methods were displayed in Table 1 and Table 2.

Table 1.

AUCs of different methods based on LDpred in the Welcome Trust Case Control Consortium Dataset.

Trait	LDpred	LDpred+STRS (p-valuea)	LDpred+MTRS (p-valueb)
Bipolar disorder	0.6574	0.6605 (0.031)	0.6626 (0.004)
Coronary artery disease	0.5965	0.5990 (0.033)	0.5998 (0.005)
Crohn’s disease	0.6293	0.6336 (9.073 × 10−4)	0.6348 (1.013 × 10−4)
Hypertension	0.5856	0.5890 (0.008)	0.5915 (3.237 × 10−4)
Rheumatoid arthritis	0.6561	0.6590 (0.017)	0.6465 (1)
Type 1 diabetes	0.7868	0.8027 (6.761 × 10−15)	0.7709 (1)
Type 2 diabetes	0.5985	0.6009 (0.034)	0.6027 (0.002)

Abbreviations: AUC, area under the curve; STRS, single-tissue transcriptional risk score; MTRS, multi-tissue transcriptional risk score.

^ap-value is based on the bootstrap test of comparing LDpred+STRS with LDpred across 100 stratified bootstrap replicates.

^bp-value is based on the bootstrap test of comparing LDpred+MTRS with LDpred across 100 stratified bootstrap replicates.

Table 2.

AUCs of different methods based on AnnoPred in the Welcome Trust Case Control Consortium Dataset.

Trait	AnnoPred	AnnoPred+STRS (p-valuea)	AnnoPred+MTRS (p-valueb)
Bipolar disorder	0.6251	0.6274 (0.007)	0.6318 (1.147 × 10−7)
Coronary artery disease	0.5967	0.6013 (0.044)	0.6015 (0.043)
Crohn’s disease	0.6924	0.6959 (0.001)	0.6966 (5.085 × 10−4)
Hypertension	0.5776	0.5799 (0.045)	0.5831 (0.003)
Rheumatoid arthritis	0.6285	0.6374 (3.361 × 10−12)	0.6394 (8.923 × 10−14)
Type 1 diabetes	0.6975	0.7027 (1.977 × 10−15)	0.7170 (<2.2 × 10−16)
Type 2 diabetes	0.6063	0.6097 (0.006)	0.6112 (2.650 × 10−4)

Abbreviations: AUC, area under the curve; STRS, single-tissue transcriptional risk score; MTRS, multi-tissue transcriptional risk score.

^ap-value is based on the bootstrap test of comparing AnnoPred+STRS with AnnoPred across 100 stratified bootstrap replicates.

^bp-value is based on the bootstrap test of comparing AnnoPred+MTRS with AnnoPred across 100 stratified bootstrap replicates.

LDpred combined with STRS showed consistently and significantly higher prediction accuracy than LDpred in seven diseases, suggesting that STRS incorporated additional information on top of LDpred to improve risk prediction (Table 1). Notably, with the addition of STRS, the AUC improved from 0.7868 to 0.8027 (p = 6.761 × 10⁻¹⁵) for T1D and from 0.6293 to 0.6336 (p = 9.073 × 10⁻⁴)for CD. These results were consistent with the observation that more significant gene associations were identified for T1D and CD in the TWAS analysis of the WTCCC dataset²⁷.

LDpred combined with MTRS performed significantly better than LDpred and slightly better than LDpred combined with STRS for BD, CAD, CD, HT, and T2D. The improved accuracy remained moderate compared to STRS, potentially due to the sharing of local expression regulation across tissues³⁸. However, the prediction accuracy of MTRS was inferior to that of STRS and even the baseline model for T1D and RA. This was probably because these two diseases showed higher tissue specificity. A previous study found that the GWAS signals of RA were mainly enriched in blood, while the GWAS signals of CAD, CD, and T2D were enriched in multiple tissues³⁹. These findings were also consistent with the observation that multi-tissue joint test could improve statistical power of gene identification when multiple tissues were related to the trait. However, if only one tissue affected the trait, the joint test was inferior to the single-tissue test in the causal tissue³⁸.

We further assessed the performance of the TRS methods when combined with AnnoPred, a PRS method that integrates functional annotations to improve prediction accuracy. When applied to the WTCCC dataset, AnnoPred combined with STRS and MTRS showed consistent and significant improvement in prediction across the seven diseases (Table 2). It is noteworthy that the advantage of TRS retained even when AnnoPred already accounted for functional annotations, further demonstrating that the TRS approach was able to capture essential information for risk prediction.

In summary, by integrating GWAS and eQTLs, the constructed STRS encompasses additional information compared to the PRS approaches. The performance of MTRS was trait-dependent, which may be related to the level of tissue specificity of the trait.

3.3. Meta-GWAS applications

Next, we trained our method with the GWAS summary statistics for CD and T2D from meta-analysis, and evaluated the performance of TRS predictors in independent datasets. Table 3 shows the AUCs of the three methods (LDpred, LDpred combined with STRS, and LDpred combined with MTRS) applied to CD and T2D. For CD, both STRS and MTRS significantly outperformed LDpred. For T2D, MTRS outperformed LDpred, while the improvement of STRS compared to LDpred was minimal. Table 4 displays the AUCs of the three methods based on AnnoPred (AnnoPred, AnnoPred combined with STRS, and AnnoPred combined with MTRS). For CD and T2D, both STRS and MTRS showed consistent and significant improvement over AnnoPred in prediction accuracy. Regardless of the baseline PRS method (LDpred or AnnoPred), the best predictive model for both CD and T2D is to combine MTRS with the corresponding baseline PRS method, which is also consistent with our results for these traits in the WTCCC datasets.

Table 3.

AUCs of different methods based on LDpred for Crohn’s disease and type 2 diabetes in the meta-GWAS studies.

Trait	LDpred	LDpred+STRS (p-valuea)	LDpred+MTRS (p-valueb)
Crohn’s disease	0.6672	0.6719 (9.159 × 10−4)	0.6753 (4.646 × 10−4)
Type 2 diabetes	0.5987	0.6008 (0.040)	0.6075 (2.089 × 10−4)

Abbreviations: AUC, area under the curve; STRS, single-tissue transcriptional risk score; MTRS, multi-tissue transcriptional risk score.

^ap-value is based on the bootstrap test of comparing LDpred+STRS with LDpred across 100 stratified bootstrap replicates.

^bp-value is based on the bootstrap test of comparing LDpred+MTRS with LDpred across 100 stratified bootstrap replicates.

Table 4.

AUCs of different methods based on AnnoPred for Crohn’s disease and type 2 diabetes in the meta-GWAS studies.

Trait	AnnoPred	AnnoPred+STRS (p-valuea)	AnnoPred+MTRS (p-valueb)
Crohn’s disease	0.7023	0.7061 (2.924 × 10−4)	0.7083 (1.888 × 10−5)
Type 2 diabetes	0.6302	0.6354 (0.002)	0.6377 (3.940 × 10−4)

Abbreviations: AUC, area under the curve; STRS, single-tissue transcriptional risk score; MTRS, multi-tissue transcriptional risk score.

^ap-value is based on the bootstrap test of comparing AnnoPred+STRS with AnnoPred across 100 stratified bootstrap replicates.

^bp-value is based on the bootstrap test of comparing AnnoPred+MTRS with AnnoPred across 100 stratified bootstrap replicates.

4. DISCUSSION

In this study, we propose a novel flexible framework for genetic risk prediction of complex traits through integrating eQTL information. Motivated by PRS formulation, we define TRS as a weighted sum of imputed gene expression and build a statistical framework that combines PRS and TRS for genetic risk prediction. Extensive simulations and real data analysis have demonstrated improved prediction accuracy by TRS methods. Specifically, when only one tissue is causally relevant to disease risk, we recommend the use of STRS. The improvement of STRS is prominent when a large extent of genetic regulation of the trait is mediated through gene expressions. However, when there are multiple tissues that independently contribute to disease risk, MTRS provides additional predictive power. In real data experiments, when using LDpred and AnnoPred as baseline PRS methods, STRS methods showed consistent and significant improvement in prediction accuracy.

There are several innovative aspects of our work. First, the TRS framework is flexible to incorporate not only GWAS summary statistics, but also re-estimations of effect sizes of individual SNPs^17–19. We expect the performance of TRS can be improved when combined with suitable PRS methods. Second, the proposed methods can be easily extended to incorporate other ‘xQTL’ information such as methylation, metabolite, and protein abundance.

Although STRS and MTRS have improvement over the existing PRS methods, we also acknowledge the following limitations. First, we used all imputed genes from the PrediXcan software without setting a p-value threshold for the genes. Imputed genes without predictive effect on the disease may bring noise to TRS. In future analysis, p-value thresholding can be used for gene selection. Second, we constructed TRS as a linear combination of imputed genes, and used it as a single score in the regression analysis (linear regression for STRS, and LASSO for MTRS). This may overlook interaction among genes, and gene regulatory networks. Machine learning models, especially nonparametric methods, can be utilized to build a more flexible model.

DATA AVAILABILITY STATEMENT

The genetic and phenotypic data in this study are not applicable for data sharing. The result data that support the findings of this study are available from the corresponding author upon reasonable request.