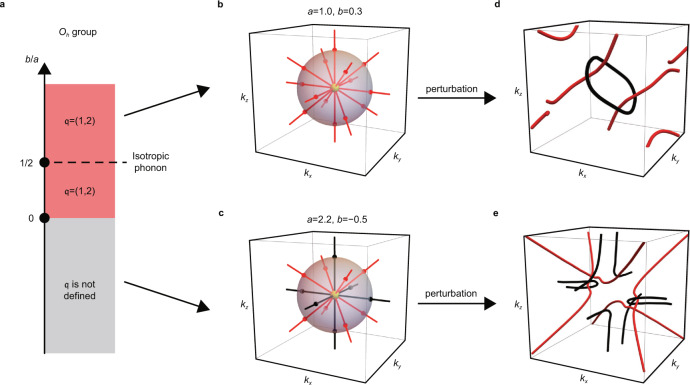
Fig. 3. Acoustic triple points in cubic systems.

a Phase diagram for the elastic continuum Hamiltonian in Eq. (2) for acoustic phonons in cubic systems. b, c Nodal structure for b/a > 0 (b) and b/a < 0 (c). The black (red) lines are band degeneracies between the upper (lower) two bands. Notice that there are two types of nodal lines, one along the k_x, k_y, and k_z axes and another along the lines that satisfy ∣k_x∣ = ∣k_y∣ = ∣k_z∣. For b/a > 0, the band degeneracies occur only between the lower two bands. However, the eigenvalues of the degenerate bands along the k_x, k_y, and k_z axes increase as b/a decreases, so that when b/a < 0, these degeneracies occur between the upper two bands instead of the lower two bands. When we perturb the Hamiltonian in b such that the conditions required to obtain the symmetry-protected TATP are broken, while the conditions needed to define $\mathfrak{q}$ are kept, we obtain d. Notice that the nodal ring (black) formed between the upper two bands are penetrated by two nodal lines formed between the lower two bands. This should be compared with e, in which we do not obtain a linked nodal ring structure as in d, although we similarly perturb the Hamiltonian in c.