Optimal Sparse Linear Prediction for Block-missing Multi-modality Data without Imputation

Abstract

In modern scientific research, data are often collected from multiple modalities. Since different modalities could provide complementary information, statistical prediction methods using multi-modality data could deliver better prediction performance than using single modality data. However, one special challenge for using multi-modality data is related to block-missing data. In practice, due to dropouts or the high cost of measures, the observations of a certain modality can be missing completely for some subjects. In this paper, we propose a new DIrect Sparse regression procedure using COvariance from Multi-modality data (DISCOM). Our proposed DISCOM method includes two steps to find the optimal linear prediction of a continuous response variable using block-missing multi-modality predictors. In the first step, rather than deleting or imputing missing data, we make use of all available information to estimate the covariance matrix of the predictors and the cross-covariance vector between the predictors and the response variable. The proposed new estimate of the covariance matrix is a linear combination of the identity matrix, the estimates of the intra-modality covariance matrix and the cross-modality covariance matrix. Flexible estimates for both the sub-Gaussian and heavy-tailed cases are considered. In the second step, based on the estimated covariance matrix and the estimated cross-covariance vector, an extended Lasso-type estimator is used to deliver a sparse estimate of the coefficients in the optimal linear prediction. The number of samples that are effectively used by DISCOM is the minimum number of samples with available observations from two modalities, which can be much larger than the number of samples with complete observations from all modalities. The effectiveness of the proposed method is demonstrated by theoretical studies, simulated examples, and a real application from the Alzheimer’s Disease Neuroimaging Initiative. The comparison between DISCOM and some existing methods also indicates the advantages of our proposed method.

1. Introduction

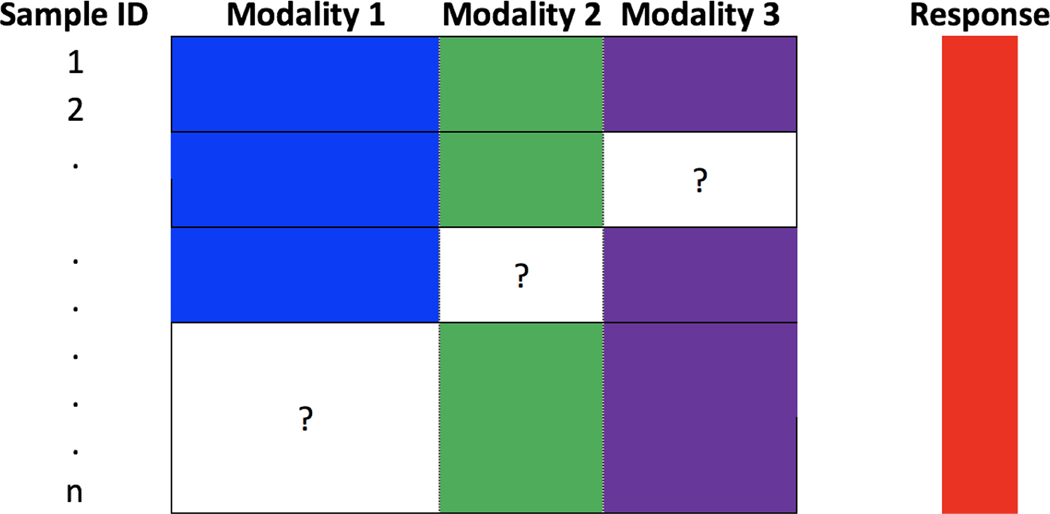
With the advance of modern scientific research, complex data are often collected from multiple modalities (sources or types). In neuroscience, different brain images such as magnetic resonance imaging (MRI) and positron emission tomography (PET) are used to study the brain structure and function. In biology, data from different modalities such as gene expressions and copy numbers are collected to understand the complex mechanism of cancers. Since different modalities could provide complementary information, statistical prediction methods using multi-modality data could deliver better prediction performance than using single modality data. However, one special challenge for using multi-modality data is related to missing data, which is unavoidable due to some reasons such as the high cost of measures or the patients’ dropout. Generally, the observations of a certain modality can be missing completely, i.e., a complete block of the data is missing. One example of block-missing multi-modality data is shown in Figure 1. In this example, there are n samples (each row represents one sample), three modalities and one response variable. The blank regions with question mark indicate missing data. As shown in Figure 1, for many samples, the observations from some modality are missing completely. The number of samples with complete observations is much smaller than the sample size n.

Figure 1:

An illustration of block-missing multi-modality data with three modalities.

To predict the response variable using the high dimensional block-missing multi-modality data, a common strategy is to use the Lasso (Tibshirani (1996)) or some other penalized regression methods (e.g., Fan and Li (2001); Zou and Hastie (2005); Zhang (2010)) only for the data with complete observations. However, this strategy can greatly reduce the sample size and waste a lot of useful information in the samples with missing data. Another strategy is to impute the missing data first by some existing imputation methods (Hastie et al. (1999); Cai et al. (2010)). These methods can be effective when the positions of the missing data are random, but they can be unstable when a complete block of the data is missing. Recently, motivated by applications in genomic data integration, Cai et al. (2016) proposed a new framework of structured matrix completion to impute block-missing data. However, they only consider the case when the data are collected from two modalities. In the literature, rather than deleting or imputing missing data, some studies focus on using all available information. For example, Yuan et al. (2012) proposed the Incomplete Multi-Source Feature learning (IMSF) method. The IMSF method performs regression on block-missing multi-modality data without imputing missing data. It formulates the prediction problem as a multi-task learning problem by first decomposing the prediction problem into a set of regression tasks, one for each combination of available modalities (e.g., modalities 1, 2 and 3; modalities 1 and 2; modalities 1 and 3; modalities 2 and 3 for the example shown in Figure 1), and then building regression models for all tasks simultaneously. The important assumption in the IMSF method is that all models involving a specific modality share the common set of predictors for that particular modality. However, when different modalities are highly correlated, this assumption could be too strong. In that case, for some modalities, it can be more reasonable to choose different predictor subsets for different involved tasks. Therefore, it is desirable to develop flexible and efficient prediction methods applicable to block-missing multi-modality data.

In this paper, we propose a new DIrect Sparse regression procedure using COvariance from Multi-modality data (DISCOM). For each sample, if some modality has missing entries, all the observations from that modality are missing simultaneously. Regardless of the underlying true model, we aim to find the optimal linear prediction for the response variable using the block-missing multi-modality data without imputing the missing data. Our method includes two steps. In the first step, we use all available information to estimate the covariance matrix of the predictors and the cross-covariance vector between the predictors and the response variable. The proposed new estimate of the covariance matrix is a linear combination of the identity matrix, the estimates of the intra-modality covariance matrix and the cross-modality covariance matrix. Flexible estimates for both the sub-Gaussian and heavy-tailed cases are considered. Many existing high dimensional covariance estimation methods such as Bickel and Levina (2008); Cai and Liu (2011); Rothman (2012); Lounici et al. (2014); Cai and Zhang (2016) can be used in this step. In the second step, based on the estimated covariance matrix and the estimated cross-covariance vector, we use an extended Lasso-type estimator to estimate the coefficients in the optimal linear prediction.

Note that there are some existing sparse regression methods in the literature using the estimation of the covariance matrix. For example, Jeng and Daye (2011) proposed the covariance-thresholded Lasso for complete data to improve variable selection by utilizing the sparsity of the covariance matrix. Loh and Wainwright (2012) and Datta et al. (2017) proposed new estimators for the high dimensional regression with corrupted predictors, where all entries of the design matrix are assumed to be noisy or missing randomly and independently. The missing data problem they considered can be viewed as a special case of the block-missing multi-modality data where each modality has only one predictor. To the best of our knowledge, there are no existing methods using a similar idea to DISCOM tailored for high-dimensional block-missing multi-modality data. To investigate DISCOM, we have carefully studied its theoretical and numerical performance. For both the sub-Gaussian and heavy-tailed cases, we establish the consistency of estimation and model selection for the optimal linear predictor regardless of the underlying true model. Our theoretical studies indicate that DISCOM could make use of all available information of the block-missing multi-modality data effectively. The number of samples that are effectively used by DISCOM is the minimum number of samples with available observations from two modalities, which can be much larger than the number of samples with complete observations from all modalities. The comparison between DISCOM and some existing methods using simulated data and the Alzheimer’s Disease Neuroimaging Initiative (ADNI) data (www.loni.ucla.edu/ADNI) further demonstrate the effectiveness of our proposed method.

The rest of this paper is organized as follows. In Section 2, we motivate and introduce our method. In Section 3, we show some theoretical results about the estimates of the covariance matrix, the cross-covariance vector and the coefficients in the optimal linear prediction for both the sub-Gaussian and heavy-tailed cases. The results about the model selection consistency are also provided. In Sections 4 and 5, we demonstrate the performance of our method on the simulated data and the ADNI dataset. We conclude this paper in Section 6 and provide all technical proofs in the Appendix.

2. Motivation and Methodology

We first show the motivation and the outline of our proposed method in Section 2.1. In Section 2.2, we introduce the proposed estimate of the covariance matrix of the predictors, and the estimate of the cross-covariance vector between the predictors and the response variable using the block-missing multi-modality data. In Section 2.3, we introduce the Huber’s M-estimate for the heavy-tailed case. In Section 2.4, we provide the estimation procedure for the coefficients in the optimal linear prediction.

The following notation will be used in this paper. For a matrix A ∈ R^m×n, we use $\Vert \mathbf{A}{\Vert }_F$, $\Vert \mathbf{\text{A}}{\Vert }_{\mathit{max}}$, and $\Vert \mathbf{\text{A}}{\Vert }_{\infty }$, to denote the Frobenius norm $\sqrt{{\sum }_{ij}{a}_{ij}^2}$, the max norm max_ij |a_ij|, and the infinity norm ${\max }_i{\sum }_{j=1}^n\left|a_{ij}\right|$, respectively. For a vector b ∈ R^m×1, we use ∥b∥₂, ∥b∥_max, and ∥b∥₁ to denote the ${\ell }_2$ norm $\sqrt{{\sum }_i{b}_i^2}$, the max norm max_i |b_i|, and the ${\ell }_1$ norm ${\sum }_{i=1}^n\left|b_i\right|$, respectively. In addition, we use sign(·) to denote the function that maps a positive entry to 1, a negative entry to −1, and 0 to 0.

2.1. Motivation

Suppose the predictors are collected from K modalities. For $k\in \{1,2,\dots ,K\}$, there are p_k predictors from the k-th modality. Let n denote the sample size, $Y={\left(y_1,y_2,\dots ,y_n\right)}^T$ denote the n × 1 response vector centered to have mean 0, and ${\mathbf{X}}^{(k)}\in R^{n\times p_k}$ denote the design matrix of the p_k predictors from the k-th modality. In addition, let $\mathbf{X}=\left({\mathbf{X}}^{(1)},{\mathbf{X}}^{(2)},\dots ,{\mathbf{X}}^{(K)}\right)={\left(x_1,x_2,\dots ,x_n\right)}^T$ denote the n × p design matrix, where $p=p_1+p_2+\cdots +p_K$. We assume that x_i’s are i.i.d. generated from some multivariate distribution with mean 0_p×1 and covariance matrix Σ. We use $C=\text{Cov}\left(x_i,y_i\right)={\left(c_1,c_2,\dots ,c_p\right)}^T\in R^p$ to denote the cross-covariance vector between x_i and y_i.

To predict the response variable y using all predictors X₁, X₂, . . ., X_p, we consider the optimal linear predictor $\widehat{y}={\sum }_{j=1}^p{X}_j{\beta }_j^0$, where the coefficient vector

$${\beta }^0={\left({\beta }_1^0,{\beta }_2^0,\dots ,{\beta }_p^0\right)}^T=\arg \underset{\beta }{\min }E\left[{\left(y-\sum _{j=1}^p{X}_j{\beta }_j\right)}^2\right]={\text{Σ}}^{-1}C.$$ (1)

The above coefficient vector β⁰ can be viewed as the solution to the following optimization problem

$$\underset{\beta }{\min }\frac{1}{2}{\beta }^T\mathbf{\Sigma }\beta -C^T\beta .$$

If we know the true covariance matrix Σ and the true cross-covariance vector C, and assume that β⁰ is sparse, we can estimate β⁰ by solving the following optimization problem

$$\underset{\beta }{\min }\frac{1}{2}{\beta }^T\mathbf{\Sigma }\beta -C^T\beta +\lambda \Vert \beta {\Vert }_1,$$ (2)

where λ is a nonnegative tuning parameter.

Motivated by (2), for the high dimensional block-missing multi-modality data, we propose a new method with two steps. In the first step, we use all available observations to estimate the covariance matrix Σ and the cross-covariance vector C. The estimates of Σ and C are denoted as $\widehat{\mathbf{\text{Σ}}}$ and $\widehat{C}$, respectively. This step is very important to make full use of the block-missing multi-modality data. In the second step, we estimate β⁰ by solving the following optimization problem:

$$\underset{\beta }{\min }\frac{1}{2}{\beta }^T\widehat{\mathbf{\Sigma }}\beta -{\widehat{C}}^T\beta +\lambda \Vert \beta {\Vert }_1.$$ (3)

2.2. Standard estimates of Σ and C

Considering block-missing multi-modality data, for each sample, if a certain modality has missing entries, all the observations from that modality are missing. For each predictor j, define S_j = {i : x_ij is not missing}. For each pair of predictors j and t, define S_jt = {i : x_ij and x_it are not missing}. The number of elements in S_j and S_jt are denoted as n_j and n_jt, respectively.

For the missing data mechanism, we only need to assume that for each predictor, the first sample moment and the second sample moment using all available observations are unbiased estimators of the first theoretical moment and the second theoretical moment of the distribution, respectively. This assumption is satisfied if we assume that each modality is missing completely at random. However, different predictors in the same modality are missing simultaneously. Under this assumption, for each j ∈ {1, 2, . . ., p}, the available observations of the j-th predictor are centered to have mean 0. A natural initial unbiased estimate of Σ using all available data is the sample covariance matrix

$$\widetilde{\mathbf{\text{Σ}}}={\left({\tilde{\sigma }}_{jt}\right)}_{j,t=1,2,\dots ,p},\text{where}{\tilde{\sigma }}_{jt}=\frac{1}{n_{jt}}\sum _{i\in S_{jt}}{x}_{ij}{x}_{it}.$$

For the block-missing multi-modality data, the above initial estimate $\widetilde{\mathbf{\text{Σ}}}$ may have negative eigenvalues due to the unequal sample sizes n_jt’s. Therefore, it is not a good estimate of the covariance matrix Σ and not suitable to be used in (3) directly. It is important to find an estimator that is both positive semi-definite and more accurate than the initial estimate $\widetilde{\mathbf{\text{Σ}}}$.

According to the partition of the predictors into K modalities, the initial estimate of the covariance matrix $\widetilde{\mathbf{\text{Σ}}}$ can be partitioned into K² blocks, denoted by ${\widetilde{\mathbf{\text{Σ}}}}_{jt}$’s, where j, t ∈ {1, 2, . . ., p} and ${\widetilde{\mathbf{\text{Σ}}}}_{jt}$ is a p_j × p_t matrix. We donte

$${\widetilde{\mathbf{\text{Σ}}}}_I=\left(\begin{array}{cccc}{\widetilde{\mathbf{\text{Σ}}}}_{11}& & & \\ & {\widetilde{\mathbf{\text{Σ}}}}_{22}& & \\ & & \ddots & \\ & & & {\widetilde{\mathbf{\text{Σ}}}}_{KK}\end{array}\right),{\widetilde{\mathbf{\text{Σ}}}}_C=\left(\begin{array}{cccc}0& {\widetilde{\mathbf{\text{Σ}}}}_{12}& \dots & {\widetilde{\mathbf{\text{Σ}}}}_{1K}\\ {\widetilde{\mathbf{\text{Σ}}}}_{21}& 0& \dots & {\widetilde{\mathbf{\text{Σ}}}}_{2K}\\ ⋮& ⋮& \ddots & ⋮\\ {\widetilde{\mathbf{\text{Σ}}}}_{K1}& {\widetilde{\mathbf{\text{Σ}}}}_{K2}& \dots & 0\end{array}\right),$$

where ${\widetilde{\mathbf{\text{Σ}}}}_I$ is called the intra-modality sample covariance matrix which is a p × p block-diagonal matrix containing K main diagonal blocks of $\widetilde{\mathbf{\text{Σ}}}$, and ${\widetilde{\mathbf{\text{Σ}}}}_C=\widetilde{\mathbf{\text{Σ}}}-{\widetilde{\mathbf{\text{Σ}}}}_I$ is called the cross-modality sample covariance matrix containing all the off-diagonal blocks of $\widetilde{\mathbf{\text{Σ}}}$. We also let Σ_I and Σ_C denote the true intra-modality covariance matrix and cross-modality covariance matrix, respectively. As shown in Figure 1, since the observations of some modalities are missing completely for many samples, there are more available samples to estimate the intra-modality covariance matrix Σ_I than the cross-modality covariance matrix Σ_C. Intuitively, it is relatively easier to estimate Σ_I than Σ_C. In view of this characteristic of the block-missing multi-modality data and the possible negative eigenvalues of $\widetilde{\mathbf{\text{Σ}}}$, we propose to use the following estimator

$$\widehat{\mathbf{\Sigma }}={\alpha }_1{\tilde{\mathbf{\Sigma }}}_I+{\alpha }_2{\tilde{\mathbf{\Sigma }}}_C+{\alpha }_3{\mathbf{I}}_{\text{p}},$$

where α₁, α₂ and α₃ are three nonrandom weights, and I_p is a p × p identity matrix. Considering all possible linear combinations, we can find the optimal linear combination ${\tilde{\mathbf{\Sigma }}}^{\ast }={\alpha }_1^{\ast }{\tilde{\mathbf{\Sigma }}}_I+{\alpha }_2^{\ast }{\tilde{\mathbf{\Sigma }}}_C+{\alpha }_3^{\ast }{\mathbf{I}}_{\mathbf{P}}$ whose expected quadratic loss $E\left[{\Vert {\widetilde{\mathbf{\text{Σ}}}}^{\ast }-\mathbf{\text{Σ}}\Vert }_F^2\right]$ is the minimum. The optimal weights ${\alpha }_1^{\ast }$, ${\alpha }_2^{\ast }$ and ${\alpha }_3^{\ast }$ are shown in the following Proposition 1. As a remark, Proposition 1 and all the theoretical analysis in Section 3 are conditional on the given missing pattern of different modalities.

Proposition 1.

Consider the following optimization problem:

$$\underset{{\alpha }_1,{\alpha }_2,{\alpha }_3}{\min }E\left[\Vert \widehat{\mathbf{\text{Σ}}}-\mathbf{\text{Σ}}{\Vert }_F^2\right]\text{subject to}\widehat{\mathbf{\text{Σ}}}={\alpha }_1{\widetilde{\mathbf{\text{Σ}}}}_I+{\alpha }_2{\widetilde{\mathbf{\text{Σ}}}}_C+{\alpha }_3{\mathbf{I}}_{\text{p}},$$

where the weights α₁, α₂ and α₃ are nonrandom. Denote ${\gamma }^{\ast }=\text{tr}(\mathbf{\Sigma })/p$, ${\delta }_I^2=E\left[\Vert {\widetilde{\mathbf{\text{Σ}}}}_I-{\mathbf{\text{Σ}}}_I{\Vert }_F^2\right]$, ${\delta }_C^2=E[{\Vert {\widetilde{\mathbf{\text{Σ}}}}_C-{\mathbf{\text{Σ}}}_C\Vert }_F^2]$, and ${\theta }^2={\Vert {\gamma }^{\ast }{\mathbf{I}}_{\text{p}}-{\mathbf{\text{Σ}}}_I\Vert }_F^2$. The optimal weights are

$${\alpha }_1^{\ast }=\frac{{\theta }^2}{{\theta }^2+{\delta }_I^2}\in [0,1],{\alpha }_2^{\ast }=\frac{{\Vert {\mathbf{\text{Σ}}}_C\Vert }_F^2}{{\Vert {\mathbf{\text{Σ}}}_C\Vert }_F^2+{\delta }_C^2}\in [0,1],{\alpha }_3^{\ast }={\gamma }^{\ast }\left(1-{\alpha }_1^{\ast }\right).$$

In addition, we have

$$E\left[{\Vert {\tilde{\mathbf{\Sigma }}}^{\ast }-\mathbf{\text{Σ}}\Vert }_F^2\right]=\frac{{\delta }_I^2{\theta }^2}{{\delta }_I^2+{\theta }^2}+\frac{{\delta }_C^2{\Vert {\mathbf{\text{Σ}}}_C\Vert }_F^2}{{\delta }_C^2+{\Vert {\mathbf{\text{Σ}}}_C\Vert }_F^2}\le {\delta }_I^2+{\delta }_C^2=E\left[\Vert \tilde{\mathbf{\Sigma }}-\mathbf{\text{Σ}}{\Vert }_F^2\right].$$

Proposition 1 shows that ${\widetilde{\mathbf{\text{Σ}}}}^{\ast }$ is more accurate than $\widetilde{\mathbf{\text{Σ}}}$. The relative improvement in the expected quadratic loss over the sample covariance matrix is equal to

$$\frac{E\left[\Vert \widetilde{\mathbf{\text{Σ}}}-\mathbf{\text{Σ}}{\Vert }_F^2\right]-E\left[{\Vert {\widetilde{\mathbf{\text{Σ}}}}^{\ast }-\mathbf{\text{Σ}}\Vert }_F^2\right]}{E\left[\Vert \widetilde{\mathbf{\text{Σ}}}-\mathbf{\text{Σ}}{\Vert }_F^2\right]}=\frac{{\delta }_I^2}{{\delta }_I^2+{\delta }_C^2}\cdot \left(1-{\alpha }_1^{\ast }\right)+\frac{{\delta }_C^2}{{\delta }_I^2+{\delta }_C^2}\cdot \left(1-{\alpha }_2^{\ast }\right).$$

Therefore, if ${\widetilde{\mathbf{\text{Σ}}}}_I$ is relatively accurate (${\delta }_I^2$ is small), the optimal weight ${\alpha }_1^{\ast }=\frac{{\theta }^2}{{\theta }^2+{\delta }_I^2}$ should be large and the percentage of the relative improvement tends to be small. We can also make the same conclusions about ${\widetilde{\mathbf{\text{Σ}}}}_C$. For the block-missing multi-modality data, due to the unequal sample sizes, the initial estimate ${\widetilde{\mathbf{\text{Σ}}}}_I$ can be relatively accurate while the estimate ${\widetilde{\mathbf{\text{Σ}}}}_C$ is relatively inaccurate. It’s reasonable to use different weights for ${\widetilde{\mathbf{\text{Σ}}}}_I$ and ${\widetilde{\mathbf{\text{Σ}}}}_C$. As a remark, Proposition 1 can be viewed as a generalization of Theorem 2.1 shown in Ledoit and Wolf (2004), where they studied the optimal linear combination of the sample covariance matrix and the identity matrix to estimate the covariance matrix for the complete data.

Regarding the cross-covariance vector C, we can use the following estimate

$$\tilde{C}={\left({\tilde{c}}_1,{\tilde{c}}_2,\cdots ,{\tilde{c}}_p\right)}^T,\text{where}{\tilde{c}}_j=\frac{1}{n_j}\sum _{i\in S_j}{y}_i{x}_{ij}.$$

Note that we use all available information to estimate Σ and C. The theoretical properties of $\widetilde{\mathbf{\text{Σ}}}$ and $\tilde{C}$ will be discussed in Section 3.

2.3. Robust estimates of Σ and C

When the predictors and the response variable follow a sub-Gaussian distribution with an exponential tail, ${\widetilde{\mathbf{\text{Σ}}}}^{\ast }$ and $\tilde{C}$ introduced in Section 2.2 generally perform well. However, when the distributions of the predictors and the response variable are heavy-tailed, ${\widetilde{\mathbf{\text{Σ}}}}^{\ast }$ and $\tilde{C}$ may have poor performance, and therefore some robust estimates of Σ and C are required.

In this section, we introduce robust estimates of Σ and C based on the Huber’s M-estimator (Huber et al. (1964)). In general, suppose Z₁, Z₂, . . ., Z_n are i.i.d. copies of a random variable Z with mean μ. The Huber’s M-estimator of μ is defined as the solution to the following equation

$$\sum _{i=1}^n{\psi }_H\left(Z_i-\mu \right)=0,$$

where ${\psi }_H(\cdot )$ is the Huber function which is given by

$${\psi }_H(z)=\{\begin{array}{ll}z& \text{if}\left|z\right|\le H,\\ H\cdot \text{sign}(z)& \text{otherwise,}\end{array}$$

Using the Huber’s M-estimator, for the block-missing multi-modality data, we can construct a robust initial estimate of Σ denoted by

$$\breve{\text{Σ}}={\left({\breve{\sigma }}_{jt}\right)}_{j,t=1,2,\dots ,p},\text{where}{\breve{\sigma }}_{jt}=\text{the solution to}\sum _{i\in S_{jt}}{\psi }_{H_{jt}}\left(x_{ij}{x}_{it}-\mu \right)=0.$$

In general, the parameters H_jt used in the Huber function can be chosen to be 1.345 in order to guarantee 95% efficiency relative to the sample mean if the data generating distribution is Gaussian (Huber et al. (1964)). However, for the block-missing multi-modality data, considering different numbers of samples available to estimate different entries of Σ, we propose to use different values of H flexibly. The choice of H_jt will be discussed in Section 3. Based on the robust initial estimate $\stackrel{⌣}{\mathbf{\text{Σ}}}$, we can use a similar idea introduced in Section 2.2 to find the optimal linear combination ${\stackrel{⌣}{\mathbf{\Sigma }}}^{\ast }={\alpha }_1^{\ast }{\breve{\mathbf{\Sigma }}}_I+{\alpha }_2^{\ast }{\mathbf{\Sigma }}_C+{\alpha }_3^{\ast }{\mathbf{I}}_{\text{p}}$ whose expected quadratic loss $E\left[{\Vert {\breve{\mathbf{\text{Σ}}}}^{\ast }-\mathbf{\text{Σ}}\Vert }_F^2\right]$ is the minimum. Similarly, we can use the Huber’s M-estimator to deliver a robust estimate of C which is defined as

$$\breve{C}={\left({\breve{c}}_1,{\breve{c}}_2,\cdots ,{\breve{c}}_p\right)}^T,\text{where}{\breve{c}}_j=\text{the solution to}\sum _{i\in S_j}{\psi }_{H_j}\left(x_{ij}{y}_i-\mu \right)=0.$$

Here we also propose to use different values of H when estimating different c_j’s. The choice of H_j will be discussed in Section 3. The theoretical properties of $\breve{\mathbf{\text{Σ}}}$ and $\breve{C}$ will be also shown in that section.

2.4. Estimate of β⁰ in the optimal linear prediction

After getting an initial estimate of Σ and C, e.g., $\widetilde{\mathbf{\text{Σ}}}$ and $\tilde{C}$ (or $\stackrel{⌣}{\mathbf{\Sigma }}$ and $\breve{C}$), our proposed DISCOM method estimates β⁰ by solving the following optimization problem:

$$\underset{\beta }{\min }\frac{1}{2}{\beta }^T\left[{\alpha }_1{\tilde{\mathbf{\Sigma }}}_I+{\alpha }_2{\tilde{\mathbf{\Sigma }}}_C+\left(1-{\alpha }_1\right)\frac{\text{tr}(\tilde{\mathbf{\Sigma }})}{p}{\mathbf{I}}_{\mathbf{p}}\right]\beta -{\tilde{C}}^T\beta +\lambda \Vert \beta {\Vert }_1,$$ (4)

where ${\alpha }_1\in [0,1]$, ${\alpha }_2\in [0,1]$ are two weights and tr($\widetilde{\mathbf{\text{Σ}}}$)/p is used to estimate γ*. In practice, both ${\alpha }_1\in [0,1]$, ${\alpha }_2\in [0,1]$, and λ can be chosen by cross validation or an additional tuning dataset. To guarantee that the estimated covariance matrix $\widehat{\mathbf{\text{Σ}}}={\alpha }_1{\widetilde{\mathbf{\text{Σ}}}}_I+{\alpha }_2{\widetilde{\mathbf{\text{Σ}}}}_C+\left(1-{\alpha }_1\right)\frac{\text{tr}(\widetilde{\mathbf{\text{Σ}}})}{p}{\mathbf{I}}_{\text{P}}$ is positive semi-definite, we need to choose reasonable α₁ and α₂ from the set $\left\{\left({\alpha }_1,{\alpha }_2\right):{\alpha }_1\in [0,1],{\alpha }_2\in [0,1],\text{and}{\lambda }_{min}(\widehat{\mathbf{\Sigma }})\ge 0\right\}$, where ${\lambda }_{\mathit{min}}(\widehat{\mathbf{\text{Σ}}})$ is the smallest eigenvalue of $\widehat{\mathbf{\text{Σ}}}$.

Besides the above tuning parameter selection method that searches for the best values of three parameters, we can use an efficient tuning method incorporating our theoretical results in Section 3. Our theoretical studies show that the tuning parameters α₁ and α₂ should satisfy the conditions $1-{\alpha }_1=O\left(\sqrt{(\log p)/{\min }_j{n}_j}\right)$ and $1-{\alpha }_2=O\left(\sqrt{(\log p)/{\min }_{j,t}{n}_{jt}}\right)$, respectively. Denote $m_1=\sqrt{(\log p)/{\min }_j{n}_j}$ and $m_2=\sqrt{(\log p)/{\min }_{j,t}{n}_{jt}}$. We can choose α₁ = 1 − k₀m₁ and α₂ = 1 − k₀m₂, where k₀ ∈ [k_min, k_max] is a tuning parameter. To guarantee that both α₁ and α₂ are nonnegative, we set k_max = min{1/m₁, 1/m₂}. In addition, a reasonable value of k₀ should satisfy the following two conditions: (1) α₁ = 1 − k₀m₁ ≤ 1 and α₂ = 1 − k₀m₂ ≤ 1; (2) the estimate of the covariance matrix $\widehat{\mathbf{\text{Σ}}}$ is positive semi-definite. The first condition requires that k₀ ≥ 0. If the smallest eigenvalue of the initial estimate $\widetilde{\mathbf{\text{Σ}}}$, denoted by λ_min($\widetilde{\mathbf{\text{Σ}}}$), is nonnegative, we can show that $\widehat{\mathbf{\text{Σ}}}$ is positive semi-definite for any nonnegative k₀. If λ_min($\widetilde{\mathbf{\text{Σ}}}$) < 0, since the smallest eigenvalue of $\widehat{\mathbf{\text{Σ}}}$ satisfies

$${\lambda }_{min}(\widehat{\mathbf{\Sigma }})\ge {\lambda }_{min}(\tilde{\mathbf{\Sigma }})+k_0\cdot \left[{\lambda }_{min}\left(\left(m_2-m_1\right){\widetilde{\mathbf{\text{Σ}}}}_I+m_1\frac{\text{tr}(\tilde{\mathbf{\Sigma }})}{p}{\mathbf{I}}_{\text{p}}\right)-m_2{\lambda }_{min}(\widetilde{\mathbf{\text{Σ}}})\right],$$

to guarantee that $\widehat{\mathbf{\text{Σ}}}$ is positive semi-definite, we only need to require that

$$k_0\ge -{\lambda }_{min}(\tilde{\mathbf{\Sigma }})/\left[-m_2\cdot {\lambda }_{min}(\tilde{\mathbf{\Sigma }})+{\lambda }_{min}\left(\left(m_2-m_1\right){\tilde{\mathbf{\Sigma }}}_I+m_1\frac{\text{tr}(\tilde{\mathbf{\Sigma }})}{p}{\mathbf{I}}_{\text{p}}\right)\right].$$

Therefore, if ${\lambda }_{\mathit{min}}(\tilde{\mathbf{\Sigma }})\ge 0$, we choose k_min = 0. Otherwise, we choose

$$k_{min}=-{\lambda }_{min}(\tilde{\mathbf{\Sigma }})/\left[-m_2\cdot {\lambda }_{min}(\tilde{\mathbf{\Sigma }})+{\lambda }_{min}\left(\left(m_2-m_1\right){\tilde{\mathbf{\Sigma }}}_I+m_1\frac{\text{tr}(\tilde{\mathbf{\Sigma }})}{p}{\mathbf{I}}_{\text{p}}\right)\right].$$

For the block-missing multi-modality data, since m₂ ≥ m₁ > 0, we know that the matrix $\left(m_2-m_1\right){\widetilde{\mathbf{\text{Σ}}}}_I+m_1\frac{\text{tr}(\widetilde{\mathbf{\text{Σ}}})}{p}{\mathbf{I}}_{\text{p}}$ is positive definite and therefore k_min is always less than $k_{\mathit{max}}=\min \left\{1/m_1,1/m_2\right\}=1/m_2$.

By choosing α₁ = 1 − k₀m₁ and α₂ = 1 − k₀m₂, our proposed fast tuning parameter selection method searches the best value of k₀ ∈ [k_min, k_max] and the parameter λ rather than searching three parameters α₁, α₂ and λ. In addition, instead of using the eigendecomposition for each parameter combination to check whether $\widehat{\mathbf{\text{Σ}}}$ is positive semi-definite, this method only requires two eigendecompositions of the matrices $\widetilde{\mathbf{\text{Σ}}}$ and $\left(m_2-m_1\right){\widetilde{\mathbf{\text{Σ}}}}_I+m_1\frac{\text{tr}(\widetilde{\mathbf{\text{Σ}}})}{p}{\mathbf{I}}_{\mathbf{\text{p}}}$ before the tuning parameter selection process. For each k₀ ∈ [k_min, k_max], we can incorporate the coordinate descent algorithm (Friedman et al. (2010)) on a grid of λ values, from the largest one down to the smallest one, using warm starts. Alternatively, since $\widehat{\mathbf{\text{Σ}}}$ is positive semi-definite, we can use the LARS algorithm shown in Jeng and Daye (2011) to compute the solution path.

As many existing high dimensional linear regression studies for the random design, we use the assumption E(X) = 0 to make our presentation more convenient. Our proposed DISCOM method can be used for the general case where E(X) ≠ 0. In that case, we first center the available observations of each predictor and use ${\overline{X}}_1,{\overline{X}}_2,\dots ,{\overline{X}}_p$ to denote the sample means of those p predictors. We also center the observed responses and use Ȳ to denote the sample mean of the response variable. Let $\widehat{\beta }$ denote the estimated regression coefficient vector calculated from the centered data. Our final predictive model is $\overline{Y}+{\sum }_{j=1}^p\left(X_j^{\ast }-{\overline{X}}_j\right){\widehat{\beta }}_j$, where $\left(X_1^{\ast },X_2^{\ast },\dots ,X_p^{\ast }\right)$ is a test data point. In practice, if our data are collected at various time points by different laboratories using multiple platforms, the i.i.d. assumption may be violated due to batch-effects. In that case, we suggest to use some existing statistical methods (e.g., the exploBATCH R package) to diagnose, quantify and correct batch effects before using our proposed DISCOM method.

3. Theoretical Study

Without loss of generalization, we assume that the true variances of all predictors, σ₁₁, σ₂₂, . . ., σ_pp, are equal to 1 in our theoretical studies. For each j ∈ {1, 2, . . ., p}, we assume that the observations of the predictor j are scaled such that ${\sum }_{i\in S_j}{x}_{ij}^2=n_j$. In that case, we have ${\tilde{\sigma }}_{jj}=1$. For the Huber’s M-estimator $\stackrel{⌣}{\mathbf{\Sigma }}$, we redefine ${\breve{\sigma }}_{jj}$ to be 1 for each j. Let $\tilde{\beta }$ and $\breve{\beta }$ denote the solutions to (4) using the sample covariance and the Huber’s M-estimator, respectively. We assume that β⁰ is sparse and denote $J=\left\{j:{\beta }_j^0\ne 0\right\}$ as the index set of the important predictors. Denote $s=|J|$ as the number of important predictors. Let ${\beta }_{\max }^0={\mathit{max}}_{j\in J}\left|{\beta }_j^0\right|$ and ${\beta }_{min}^0={\min }_{j\in J}\left|{\beta }_j^0\right|$. In Sections 3.1 and 3.2, we will discuss the theoretical properties in the sub-Gaussian case and the heavy-tailed case, respectively. The model selection consistency of our proposed method will be shown in Section 3.3.

3.1. Sub-Gaussian case

The following conditions are considered in this section:

(A1) Suppose that there exists a constant L > 0 such that

$$E\left(\exp \left(t{X}_j\right)\right)\le \exp \left(\frac{L^2{t}^2}{2}\right)\text{for all}j\in \{1,2,\dots ,p\}\text{and}t\in R,$$

$$E(\exp (ty))\le \exp \left(\frac{L^2{t}^2}{2}\right)\text{for all}t\in R.$$

(A2) Suppose that the true covariance matrix Σ satisfies the following restricted eigenvalue (RE) condition

$$\underset{\delta \in \left\{u\in R^p:{\Vert u_{Jc}\Vert }_1\le 7{\Vert u_J\Vert }_1\right\}}{\min }\frac{{\delta }^T\mathbf{\text{Σ}}\delta }{{\delta }^T\delta }\ge m>0.$$

Under condition (A1), the predictors and the response variable follow sub-Gaussian distributions with exponentially bounded tails. In this case, we propose to use $\widetilde{\mathbf{\text{Σ}}}$ and $\tilde{C}$ shown in Section 2.2 as the initial estimate of the covariance matrix Σ and the cross-covariance vector C, respectively. The RE condition (A2) is often used to obtain bounds of statistical error of the Lasso estimate (Datta et al. (2017)). The following Theorem 1 shows the large deviation bounds of $\widetilde{\mathbf{\text{Σ}}}$ and $\tilde{C}$.

Theorem 1.

Under condition (A1), if min_j,t n_jt ≥ 6 log p, there exists two positive constants ν₁ = 8$\sqrt{6}$(1 + 4L²) and ν₂ = 4 such that

$$\underset{j,t}{\max }P\left(\left|{\tilde{\sigma }}_{jt}-{\sigma }_{jt}\right|\ge {\nu }_1\sqrt{\frac{\log p}{n_{jt}}}\right)\le \frac{{\nu }_2}{p^3},P\left(\Vert \widetilde{\mathbf{\text{Σ}}}-\mathbf{\text{Σ}}{\Vert }_{max}\ge {\nu }_1\sqrt{\frac{\log p}{{\min }_{j,t}{n}_{jt}}}\right)\le \frac{{\nu }_2}{p}.$$

There exists another two positive constants ${\nu }_3=16\left(1+4\frac{L^2}{\min \{\mathrm{var}(y),1\}}\right)\max \{\mathrm{var}(y),1\}$ and ν₄ = 4 such that

$$\underset{j}{\max }P\left(\left|{\tilde{c}}_j-c_j\right|\ge {\nu }_3\sqrt{\frac{\log p}{n_j}}\right)\le \frac{{\nu }_4}{p^2},P\left(\Vert \tilde{C}-C{\Vert }_{\mathit{max}}\ge {\nu }_3\sqrt{\frac{\log p}{{\min }_j{n}_j}}\right)\le \frac{{\nu }_4}{p}.$$

Remark 1.

In our theoretical studies, we assume that the dimension p goes to infinity as the sample size min_j,t n_jt increases. If we further assume that (log p)/min_j,t n_jt = o(1), the condition min_j,t n_jt > 6 log p is satisfied if the sample size min_j,t n_jt is sufficiently large. Then, Theorem 1 shows that $\Vert \widetilde{\mathbf{\text{Σ}}}-\mathbf{\text{Σ}}{\Vert }_{\mathit{max}}=O_p\left(\sqrt{(\log p)/{\min }_{j,t}{n}_{jt}}\right)$. The performance of $\widetilde{\mathbf{\text{Σ}}}$ depends on the worst case when there are only min_j,t n_jt samples to estimate some entries in Σ. In addition, the convergence rate of $\Vert \tilde{C}-C{\Vert }_{\mathit{max}}$ is $O_p\left(\sqrt{(\log p)/{\min }_j{n}_j)}\right)$. The performance of $\tilde{C}$ also depends on the worst case when there are only min_j n_j samples to estimate the covariance between some predictor and the response variable. Furthermore, if we only use samples with complete observations, using a similar proof, we can show that $\Vert \widetilde{\mathbf{\text{Σ}}}-\mathbf{\text{Σ}}{\Vert }_{max}=O_p\left(\sqrt{(\log p)/n_{complete}}\right)$ and $\Vert \tilde{C}-C{\Vert }_{max}=O_p\left(\sqrt{(\log p)/n_{complete}}\right)$, where n_complete is the number of samples with complete observations. For the block-missing multi-modality data, since n_complete can be much smaller than min_j,t n_jt and min_j n_j, Theorem 1 indicates that the first step of our proposed DISCOM method can make full use of all available information. Based on the results shown in Theorem 1, we will show the convergence rate of ${\Vert \tilde{\beta }-{\beta }^0\Vert }_2$.

Theorem 2.

Under conditions (A1) and (A2), let $1-{\alpha }_1=O\left(\sqrt{(\log p)/{\min }_j{n}_j}\right)$ and $1-{\alpha }_2=O\left(\sqrt{(\log p)/{\min }_{j,t}{n}_{jt}}\right)$. If $s\sqrt{(\log p)/{\min }_{j,t}{n}_{jt}}=o(1)$ and we choose $\lambda =2{\Vert \tilde{C}-\widehat{\mathbf{\Sigma }}{\beta }^0\Vert }_{max}$, then we have ${\Vert \tilde{\beta }-{\beta }^0\Vert }_2=O_p(\sqrt{s}\lambda )=O_p\left({\Vert {\beta }^0\Vert }_1\sqrt{s(\log p)/{\min }_{j,t}{n}_{jt}}\right)$.

Remark 2.

As shown in the above Theorem 2, we have ${\Vert \tilde{\beta }-{\beta }^0\Vert }_2=O_p(\sqrt{s}\Vert \tilde{C}-\widehat{\mathbf{\text{Σ}}}{\beta }^0{\Vert }_{max})$. If we assume that (a) there is no missing data, (b) the predictors are generated from a multivariate Gaussian distribution, and (c) the true model is Y = Xβ⁰ + ϵ, where ϵ ∼ N(0, σ²I_n). Then we will use $\widehat{\mathbf{\text{Σ}}}={\mathbf{X}}^T\mathbf{X}/n$ and $\tilde{C}={\mathbf{X}}^{T}Y/n$ to estimate Σ and C, respectively. Therefore, we have ${\Vert \tilde{C}-\widehat{\mathbf{\text{Σ}}}{\beta }^0\Vert }_{max}={\Vert {\mathbf{X}}^T\mathit{ϵ}/n\Vert }_{max}=O_p(\sqrt{(\log p)/n})$, and ${\Vert \tilde{\beta }-{\beta }^0\Vert }_2=O_p(\sqrt{(s\log p)/n})$, which is the minimax ℓ₂-norm rate as shown in Raskutti et al. (2011). Since the complete data generated from the Gaussian random design can be viewed as a special type of block-missing multi-modality data, the error bound in Theorem 2 is sharp.

On the other hand, if the true relationship between the conditional expectation $E\left(y\mid X_1,X_2,\dots ,X_p\right)$ and the predictors is non-linear, we have $\tilde{C}-\widehat{\mathbf{\text{Σ}}}{\beta }^0\ne {\mathbf{X}}^T\mathit{ϵ}/n$ and ${\Vert \tilde{C}-\widehat{\mathbf{\text{Σ}}}{\beta }^0\Vert }_{\mathit{max}}=O_p\left({\Vert {\beta }^0\Vert }_1\sqrt{(\log p)/n}\right)$ as shown in the proof. In this case, if we still use the Lasso method to estimate the regression coefficients β⁰ in the optimal linear predictor, we have ${\Vert {\tilde{\beta }}_{\mathit{\text{Lasso}}}-{\beta }^0\Vert }_2=O_p\left({\Vert {\beta }^0\Vert }_1\sqrt{s(\log p)/n}\right)$. For the blocking missing multi-modality data, since the Lasso method can only use the data with complete observations, we have ${\Vert {\tilde{\beta }}_{Lasso}-{\beta }^0\Vert }_2=O_p\left({\Vert {\beta }^0\Vert }_1\sqrt{s(\log p)/n_{complete}}\right)$. However, as shown in Theorem 2, for our proposed DISCOM estimate $\tilde{\beta }$, we have ${\Vert \tilde{\beta }-{\beta }^0\Vert }_2=O_p\left({\Vert {\beta }^0\Vert }_1\sqrt{s(\log p)/{\min }_{j,t}{n}_{jt}}\right)$. In practice, the minimum number of samples with available observations from two modalities (min_j,t n_jt) can be much larger than the number of samples with complete observations from all modalities (n_complete). Theorem 2 indicates that DISCOM could make use of the block-missing multi-modality data more effectively than the Lasso method using only the complete data.

In Theorem 2, the assumption $s\sqrt{(\log p)/{\min }_{j,t}{n}_{jt}}=o(1)$ is used to guarantee that $\widehat{\mathbf{\text{Σ}}}$ satisfies the RE condition with a high probability if the true covariance matrix Σ satisfies the RE condition (A2). Note that many existing sparse linear regression studies focus on the fixed design where the design matrix X is considered to be fixed and complete. In that case, $\widehat{\mathbf{\text{Σ}}}={\mathbf{X}}^T\mathbf{X}/n$ is assumed to satisfy the RE condition directly. For the general random design, Van De Geer et al. (2009) showed that $\widehat{\mathbf{\text{Σ}}}={\mathbf{X}}^T\mathbf{X}/n$ satisfies the RE condition as long as the true covariance matrix $\mathbf{\text{Σ}}$ satisfies the RE condition and s² logp/n = o(1). For the special Gaussian random design, by a global analysis of the full random matrix $\widehat{\mathbf{\text{Σ}}}={\mathbf{X}}^T\mathbf{X}/n$ rather than a local analysis looking at individual entries of $\widehat{\mathbf{\text{Σ}}}$, Raskutti et al. (2010) shows that the matrix $\widehat{\mathbf{\text{Σ}}}$ satisfies the RE condition with a high probability if the true covariance matrix of the multivariate Gaussian distribution satisfies the RE condition and n > Constant·s log p. In our paper, since we consider the general random design including both sub-Gaussian distributions and heavy-tailed distributions, and study the proposed estimated covariance matrix $\widehat{\mathbf{\text{Σ}}}$ where $\widehat{\mathbf{\text{Σ}}}\ne {\text{X}}^T\text{X}/n$ in most cases, we use the condition $s\sqrt{(\log p)/{\min }_{j,t}{n}_{jt}}=o(1)$ to guarantee that the RE condition is satisfied with a high probability. This condition is very similar to the condition $s^2\log p/n=o(1)$ used in Van De Geer et al. (2009) for the complete data.

For the general random design and the block-missing multi-modality data, it is difficult to develop a weak condition (e.g., s log p/min_j,t n_jt = o(1)) using a similar global analysis of the full random matrix $\widehat{\mathbf{\text{Σ}}}$ as shown in Raskutti et al. (2010). Instead of using the condition $s\sqrt{(\log p)/{\min }_{j,t}{n}_{jt}}=o(1)$, we can use the following weak condition

$$\underset{j,t}{\min }{n}_{jt}>{\left(128{\nu }_1^{\prime }/m\right)}^2\left(s^2\log p\right),$$

where ${\nu }_1^{\prime }>{\nu }_1$ is a positive constant. This condition is also used in some existing studies about random designs (Bühlmann and Van De Geer (2011); Zhou et al. (2009)).

3.2. Heavy-tailed case

In this section, we consider the heavy-tailed case. Instead of assuming that the distributions of the predictors and the response variable have exponential tails, we consider the following moment condition.

(A3) Suppose that max ${\max }_{1\le j\le p}\text{E}\left(X_j^4\right)\le Q_1^2/48$ and $\text{E}\left(y^4\right)\le Q_2^2$, where Q₁ and Q₂ are two positive constants.

Condition (A3) assumes that the fourth moments of all predictors X_j’s and the response variable y are bounded. Under condition (A3), the tails of the distributions of X_j’s and y may not be exponentially bounded. In the literature on Lasso, most studies consider the fixed design (Zhao and Yu (2006); Zou (2006); Meinshausen and Bühlmann (2006)) and the noise is usually assumed to be Gaussian (Meinshausen and Bühlmann (2006); Zhang et al. (2008)), or admits exponentially bounded tail (Bunea et al. (2008); Meinshausen and Yu (2009)). In this study, we consider a random design case and relax the distribution of X_j’s and y to have finite fourth moments.

Next, we discuss the theoretical properties of the Huber’s M-estimators $\stackrel{⌣}{\mathbf{\text{Σ}}}$ and $\breve{C}$. Based on the convergence rates of $\Vert \breve{\mathbf{\text{Σ}}}-\mathbf{\text{Σ}}{\Vert }_{max}$ and $\Vert \breve{C}-C{\Vert }_{max}$, we will show the convergence rate of ${\Vert \breve{\beta }-{\beta }^0\Vert }_2$.

Theorem 3.

Under condition (A3), let $H_{jt}=\frac{Q_1}{12}\sqrt{n_{jt}/\log p}$ for each j, t ∈ {1, 2, . . ., p}, if min_j,t n_jt ≥ 24 log p, we have

$$\underset{j,t}{\max }P\left(\left|{\breve{\sigma }}_{jt}-{\sigma }_{jt}\right|\ge Q_1\sqrt{\frac{\log p}{n_{jt}}}\right)\le \frac{2}{p^3},$$

$$P\left(\Vert \stackrel{⌣}{\mathbf{\Sigma }}-\mathbf{\text{Σ}}{\Vert }_{max}\ge Q_1\sqrt{\frac{\log p}{{\min }_{j,t}{n}_{jt}}}\right)\le \frac{2}{p}.$$

In addition, let $H_j=\left(Q_1+Q_2\right)\sqrt{n_j/\log p}$ for each $j\in \{1,2,\dots ,p\}$, we have

$$\underset{j}{\max }P\left(\left|{\breve{c}}_j-c_j\right|\ge 8\left(Q_1+Q_2\right)\sqrt{\frac{\log p}{n_j}}\right)\le \frac{2}{p^2},$$

$$P\left(\Vert \breve{C}-C{\Vert }_{max}\ge 8\left(Q_1+Q_2\right)\sqrt{\frac{\log p}{{\min }_j{n}_j}}\right)\le \frac{2}{p}.$$

Remark 3.

If we assume that (log p)/min_j,t n_jt = o(1), the condition min_j,t n_jt > 24 log p is satisfied if the sample size min_j,t n_jt is sufficiently large. Therefore, we have $\Vert \stackrel{⌣}{\mathbf{\Sigma }}-\mathbf{\text{Σ}}{\Vert }_{\mathit{max}}=O_p\left(\sqrt{(\log p)/{\min }_{j,t}{n}_{jt}}\right)$ and $\Vert \breve{C}-C{\Vert }_{max}=O_p\left(\sqrt{(\log p)/{\min }_j{n}_j}\right)$. This indicates that the Huber’s M-estimators for the heavy-tailed case acquire the same convergence rate as the sample covariance estimates for the sub-Gaussian case. However, as shown in the next theorem, if the distributions of the predictors X_j’s and the response variable y are not assumed to have exponentially bounded tails, the large deviation bounds of $\widetilde{\text{Σ}}$ and $\tilde{C}$ can be wider than the bounds of the Huber’s M-estimators $\stackrel{⌣}{\text{Σ}}$ and $\breve{C}$, respectively.

Theorem 4.

Suppose ${\max }_{1\le j\le p}\text{E}\left(X_j^{4\ell }\right)\le T$ and $\text{E}\left(y^{4\ell }\right)\le T$, where T > 0, ℓ > 1 are two constants. Then we have

$$\underset{j,t}{\max }P\left(\left|{\tilde{\sigma }}_{jt}-{\sigma }_{jt}\right|\ge \frac{d_1}{2T}\sqrt{\frac{p}{n_{jt}}}\right)\le \frac{d_2}{p^{2h}},P\left(\Vert \widetilde{\mathbf{\text{Σ}}}-\text{Σ}{\Vert }_{\mathit{max}}\ge \frac{d_1}{2T}\sqrt{\frac{p}{{\min }_{j,t}{n}_{jt}}}\right)\le \frac{d_2}{p^{2h-2}},$$

where d₁ > 0, d₂ > 0, h ∈ (1, ℓ) are some constants. Furthermore,

$$\underset{j}{\max }P\left(\left|{\tilde{c}}_j-c_j\right|\ge \frac{d_3}{2T}\sqrt{\frac{p}{n_j}}\right)\le \frac{d_4}{p^{2h-1}},P\left(\Vert \tilde{C}-C{\Vert }_{max}\ge \frac{d_3}{2T}\sqrt{\frac{p}{{\min }_j{n}_j}}\right)\le \frac{d_4}{p^{2h-2}},$$

where d₃ > 0 and d₄ > 0 are two constants.

Remark 4.

Under the moment condition, Theorem 4 shows that $\Vert \widetilde{\mathbf{\text{Σ}}}-\mathbf{\text{Σ}}{\Vert }_{max}=O_p\left(\sqrt{p/{\min }_{j,t}{n}_{jt}}\right)$ and $\Vert \tilde{C}-C{\Vert }_{max}=O_p\left(\sqrt{p/{\min }_j{n}_j}\right)$. According to the Proposition 6.2 in Catoni (2012), the bounds shown in Theorem 4 are actually tight. If the dimension p is very large, the large deviation bounds of $\Vert \widetilde{\mathbf{\text{Σ}}}-\mathbf{\text{Σ}}{\Vert }_{\max }$ and $\Vert \tilde{C}-C{\Vert }_{\mathit{max}}$ can be much larger than the bounds of $\Vert \stackrel{⌣}{\mathbf{\Sigma }}-\mathbf{\text{Σ}}{\Vert }_{max}$ and $\Vert \breve{C}-C{\Vert }_{max}$, respectively. This necessitates the usage of a robust estimator.

In the next theorem, based on the large deviation bounds of $\Vert \stackrel{⌣}{\mathbf{\text{Σ}}}-\mathbf{\text{Σ}}{\Vert }_{max}$ and $\Vert \breve{C}-C{\Vert }_{\mathit{max}}$, we show the convergence rate of ${\Vert \breve{\beta }-{\beta }^0\Vert }_2$.

Theorem 5.

Under conditions (A2) and (A3), let $1-{\alpha }_1=O\left(\sqrt{(\log p)/{\min }_j{n}_j}\right)$, $1-{\alpha }_2=O\left(\sqrt{(\log p)/{\min }_{j,t}{n}_{jt}}\right)$, $H_{jt}=\frac{Q_1}{12}\sqrt{n_{jt}/\log p}$ and $H_j=\left(Q_1+Q_2\right)\sqrt{n_j/\log p}$. If $s\sqrt{(\log p)/{\min }_{j,t}{n}_{jt}}=o(1)$ and let $\lambda =2{\Vert \breve{C}-\widehat{\mathbf{\text{Σ}}}{\beta }^0\Vert }_{max}$, then we have ${\Vert \breve{\beta }-{\beta }^0\Vert }_2=O_p(\sqrt{s}\lambda )=O_p\left({\Vert {\beta }^0\Vert }_1\sqrt{s(\log p)/{\min }_{j,t}{n}_{jt}}\right)$.

Remark 5.

Instead of using the condition $s\left(\sqrt{(\log p)/{\min }_{j,t}{n}_{jt}}\right)$ = o(1), we can assume that

$$\underset{j,t}{\min }{n}_{jt}>{\left(128Q_1^{\prime }/m\right)}^2\left(s^2\log p\right),$$

where $Q_1^{\prime }>Q_1$ is a positive constant. Theorem 5 indicates that for the heavy-tailed case, under (A3), the convergence rate of ${\Vert \breve{\beta }-{\beta }^0\Vert }_2$ is also $O_p\left(\Vert {\beta }^0{\Vert }_1\sqrt{(s\log p)/{\min }_{j,t}{n}_{jt}}\right)$, which is the same as the rate shown in Theorem 2 under the sub-Gaussian assumption. However, as shown in our simulation study, if the response variable and the predictors follow sub-Gaussian distributions, DISCOM using standard estimates $\widetilde{\mathbf{\text{Σ}}}$ and $\tilde{C}$ generally has better finite sample performance than the method using robust estimates $\breve{\text{Σ}}$ and $\breve{C}$.

Remark 6.

If we assume that p is fixed, for the sub-Gaussian case considered in Section 3.1, we can show that $\Vert \widetilde{\mathbf{\text{Σ}}}-\mathbf{\text{Σ}}{\Vert }_{max}=O_p\left({\left({\min }_{j,t}{n}_{jt}\right)}^{-1/2}\right)$ and $\Vert \tilde{C}-C{\Vert }_{max}=O_p\left({\left({\min }_j{n}_j\right)}^{-1/2}\right)$ according to Lemma 1 in Ravikumar et al. (2011) and a very similar proof of Theorem 1. For the heavy-tailed case considered in Section 3.2, if we assume that p is fixed, we can also show that $\Vert \stackrel{⌣}{\mathbf{\Sigma }}-\mathbf{\text{Σ}}{\Vert }_{max}=O_p\left({\left({\min }_{j,t}{n}_{jt}\right)}^{-1/2}\right)$ and $\Vert \breve{C}-C{\Vert }_{max}=O_p\left({\left({\min }_j{n}_j\right)}^{-1/2}\right)$ according to Theorem 5 in Fan et al. (2016) and a very similar proof of Theorem 3. Then, using the same proof of Theorem 2, we can also show that $\Vert \tilde{\beta }-{\beta }^0{\Vert }_2=O_p(\sqrt{s}\lambda )=O_p\left(\sqrt{s}\Vert \tilde{C}-\widehat{\mathbf{\text{Σ}}}{\beta }^0{\Vert }_{max}\right)$. Since $\Vert \widetilde{\mathbf{\text{Σ}}}-\mathbf{\text{Σ}}{\Vert }_{max}=O_p\left({\left({\min }_{j,t}{n}_{jt}\right)}^{-1/2}\right)$, $\Vert \tilde{C}-C{\Vert }_{max}=O_p\left({\left({\min }_j{n}_j\right)}^{-1/2}\right)$, and p is fixed, we can further show that ${\Vert \tilde{\beta }-{\beta }^0\Vert }_2=O_p\left({\beta }_{max}^0{\left({\min }_{j,t}{n}_{jt}\right)}^{-1/2}\right)$. Similarly, for the heavy-tailed case, we can also show that ${\Vert \breve{\beta }-{\beta }^0\Vert }_2=O_p\left({\beta }_{\mathit{max}}^0{\left({\min }_{j,t}{n}_{jt}\right)}^{-1/2}\right)$. Therefore, the convergence rate of the estimation error in the classical fixed p setting is faster than the rate in the high dimensional setting where p grows to infinity.

3.3. Model selection consistency

In this section, we show that our proposed DISCOM method is model selection consistent. The following condition is considered.

(A4) ${\Vert {\mathbf{\text{Σ}}}_{J^{c}J}{\mathbf{\text{Σ}}}_{JJ}^{-1}\Vert }_{\infty }\le 1-\eta$, where η ∈ (0, 1) is a constant, ${\mathbf{\text{Σ}}}_{J^{c}J}$ is the sub-matrix of Σ with row indices in the set J^c and column indices in the set J, and Σ_JJ is the sub-matrix of Σ with both row and column indices in the set J.

Condition (A4) can be viewed as a population version of the strong irrepresentable condition proposed in Zhao and Yu (2006). In the following Theorem 6 and Theorem 7, we will show that our proposed DISCOM method is model selection consistent for the sub-Gaussian case and the heavy-tailed case, respectively.

Theorem 6.

Under conditions (A1) and (A4), let $1-{\alpha }_1=O\left(\sqrt{(\log p)/{\min }_j{n}_j}\right)$ and $1-{\alpha }_2=O\left(\sqrt{(\log p)/{\min }_{j,t}{n}_{jt}}\right)$. If ${\Vert {\left({\sum }_{JJ}\right)}^{-1}\Vert }_{\infty }\cdot \sqrt{\frac{s^2\log p}{{\min }_{j,t}{n}_{jt}}}\to 0$, and

$$\frac{1+s{\beta }_{max}^0}{\lambda }\sqrt{\frac{\log p}{{\min }_{j,t}{n}_{jt}}}\to 0,\frac{\lambda \cdot {\Vert {\left({\text{Σ}}_{JJ}\right)}^{-1}\Vert }_{\infty }}{{\beta }_{min}^0}\to 0,$$

then there exists a solution $\tilde{\beta }$ to (4) such that $P\left(\text{sign}(\tilde{\beta })=\text{sign}\left({\beta }^0\right)\right)\to 1$, as min_jt n_jt → ∞ and p → ∞.

Remark 7.

Note that the condition ${\Vert {\left({\mathbf{\text{Σ}}}_{JJ}\right)}^{-1}\Vert }_{\infty }\cdot \sqrt{\left(s^2\log p\right)/{\min }_{j,t}{n}_{jt}}=o(1)$ is used to guarantee that (a) ${\Vert {\left({\widehat{\mathbf{\text{Σ}}}}_{JJ}\right)}^{-1}\Vert }_{\infty }\le \text{Constant}\cdot {\Vert {\left({\text{Σ}}_{JJ}\right)}^{-1}\Vert }_{\infty }$ and (b) ${\Vert {\widehat{\mathbf{\text{Σ}}}}_{J^{c}J}{\widehat{\mathbf{\sum }}}_{JJ}^{-1}\Vert }_{\infty }\le 1-{\eta }^{\prime }$ if ${\Vert {\mathbf{\Sigma }}_{J^{c}J}{\mathbf{\Sigma }}_{JJ}^{-1}\Vert }_{\infty }\le 1-\eta$ for the general random design with a high probability, where ${\eta }^{\prime }\in (0,1)$ and η ∈ (0, 1) are two constants. For the fixed design, we do not need this condition. For the special Gaussian random design, as shown in Wainwright (2009), using some concentration inequalities about the normal distribution and the fact that $\widehat{\mathbf{\text{Σ}}}={\mathbf{\text{X}}}^T\mathbf{\text{X}}/n$ for the complete data, we can obtain model selection consistency with n > Constant · s log(p − s). In our theoretical studies, since we consider the general random design including both sub-Gaussian distributions and heavy-tailed distributions, and $\widehat{\mathbf{\text{Σ}}}\ne {\mathbf{X}}^T\mathbf{X}/n$ for the block-missing multi-modality data, we use the condition ${\Vert {\left({\mathbf{\text{Σ}}}_{JJ}\right)}^{-1}\Vert }_{\infty }\cdot \sqrt{\left(s^2\log p\right)/{\min }_{j,t}{n}_{jt}}=o(1)$ to guarantee that (a) and (b) are satisified. Note that this condition was also used in some existing model selection consistency studies for random designs (Jeng and Daye (2011); Datta et al. (2017)).

As shown in the proof of Theorem 6, to guarantee that (a) and (b) are satisfied, instead of requiring ${\Vert {\left({\mathbf{\text{Σ}}}_{JJ}\right)}^{-1}\Vert }_{\infty }\cdot \sqrt{\left(s^2\log p\right)/{\min }_{j,t}{n}_{jt}}=o(1)$, we can use the following weak condition

$${\Vert {\left({\mathbf{\text{Σ}}}_{JJ}\right)}^{-1}\Vert }_{\infty }\cdot \sqrt{\frac{s^2\log p}{{\min }_{j,t}{n}_{jt}}}\le \frac{\eta }{{\nu }_1^{\prime }(4+\eta )},$$

where ${\nu }_1^{\prime }>{\nu }_1$ is a positive constant.

Theorem 7.

Under conditions (A3) and (A4), let $H_{jt}=\frac{Q_1}{12}\sqrt{n_{jt}/\log p}$, $H_j=\left(Q_1+Q_2\right)\sqrt{n_j/\log p}$, $1-{\alpha }_1=O\left(\sqrt{(\log p)/{\min }_j{n}_j}\right)$, $1-{\alpha }_2=O\left(\sqrt{(\log p)/{\min }_{j,t}{n}_{jt}}\right)$. If ${\Vert {\left({\mathbf{\text{Σ}}}_{JJ}\right)}^{-1}\Vert }_{\infty }\cdot \sqrt{\left(s^2\log p\right)/{\min }_{j,t}{n}_{jt}}\to 0$, and

$$\frac{1+s{\beta }_{max}^0}{\lambda }\sqrt{\frac{\log p}{{\min }_{j,t}{n}_{jt}}}\to 0,\frac{\lambda \cdot {\Vert {\left({\mathbf{\text{Σ}}}_{JJ}\right)}^{-1}\Vert }_{\infty }}{{\beta }_{min}^0}\to 0,$$

then there exists a solution $\breve{\beta }$ to (4) such that $P\left(\text{sign}(\breve{\beta })=\text{sign}\left({\beta }^0\right)\right)\to 1$, as ${\min }_{jt}{n}_{jt}\to \infty$ and $p\to \infty$.

Remark 8.

Instead of requiring ${\Vert {\left({\mathbf{\text{Σ}}}_{JJ}\right)}^{-1}\Vert }_{\infty }\cdot \sqrt{\left(s^2\log p\right)/{\min }_{j,t}{n}_{jt}}=o(1)$, we can use the following weak condition

$${\Vert {\left({\mathbf{\text{Σ}}}_{JJ}\right)}^{-1}\Vert }_{\infty }\cdot \sqrt{\frac{s^2\log p}{{\min }_{j,t}{n}_{jt}}}\le \frac{\eta }{Q_1^{\prime }(4+\eta )},$$

where $Q_1^{\prime }>Q_1$ is a positive constant. The proof of Theorem 7 is very similar to the proof of Theorem 6. We only show the proof of Theorem 7 briefly in the Appendix.

4. Simulation Study

In this section, we perform numerical studies using simulated examples. We use DISCOM and DISCOM-Huber to denote our proposed methods using sample covariance estimates and Huber’s M-estimates, respectively. The proposed methods using the fast tuning parameter selection method shown in Section 2.4 are called Fast-DISCOM and Fast-DISCOM-Huber, respectively. For each example, we compare our proposed methods with 1) Lasso: Lasso method which only uses the samples with complete observations; 2) Imputed-Lasso: Lasso method which uses all samples with missing data imputed by the Soft-thresholded SVD method (Mazumder et al. (2010)); 3) Ridge: Ridge regression method which only uses the samples with complete observations; 4) Imputed-Ridge: Ridge regression method which uses all samples with missing data imputed by the Soft-thresholded SVD method; and 5) IMSF (Yuan et al. (2012)): the IMSF method which uses all available data without imputing the missing data. We study four simulated examples, where the data are generated from the Gaussian distribution or some heavy-tailed distributions.

For each example, the data are generated from three modalities and each modality has 100 predictors. The training data set is composed of 100 samples with complete observations, 100 samples with observations from the first and the second modalities, 100 samples with observations from the first and the third modalities, and 100 samples with observations only from the first modality. The tuning data set contains 200 samples with complete observations and the testing data set contains 400 samples with complete observations. All methods use the tuning data set to choose the best tuning parameters. For the four simulated examples, samples with complete observations are generated from the linear model as follows.

Example 1:

The predictors ${\left(x_{i1},x_{i2},\dots ,x_{ip}\right)}^T\sim N(0,\mathbf{\Sigma })$ with ${\sigma }_{jt}={0.6}^{|j-t|}$. The true coefficient vector

$${\beta }^0=(0.5,0.5,0.5,\underset{97}{\underbrace{0,\cdots ,0}},0.5,0.5,0.5,\underset{97}{\underbrace{0,\cdots ,0}},0.5,0.5,0.5,\underset{97}{\underbrace{0,\cdots ,0}}).$$

The true model is $Y=\mathbf{X}{\beta }^0+\mathit{ϵ}$, where the errors ${ϵ}_1,{ϵ}_2,\dots ,{ϵ}_n\stackrel{i.i.d}{\sim }N(0,1)$.

Example 2:

The predictors ${\left(x_{i1},x_{i2},\dots ,x_{ip}\right)}^T\sim N(0,\mathbf{\text{Σ}})$, where Σ is a block diagonal matrix with p/5 blocks. Each block is a 5 × 5 square matrix with ones on the main diagonal and 0.15 elsewhere. The true coefficient vector

$${\beta }^0=\left(\underset{5}{\underbrace{0.5,\cdots ,0.5}},\underset{95}{\underbrace{0,\cdots ,0}},\underset{5}{\underbrace{0.5,\cdots ,0.5}},\underset{95}{\underbrace{0,\cdots ,0}},\underset{5}{\underbrace{0.5,\cdots ,0.5}},\underset{95}{\underbrace{0,\cdots ,0}}\right).$$

The true model is $Y=\mathbf{X}{\beta }^0+\mathit{ϵ}$, where the errors ${ϵ}_1,{ϵ}_2,\dots ,{ϵ}_n\stackrel{i.i.d}{\sim }N(0,1)$.

Example 3:

The predictors ${\left(x_{i1},x_{i2},\dots ,x_{ip}\right)}^T\sim t_5(\mathbf{0},0.6\mathbf{\text{Σ}})$, where Σ is the same as the covariance matrix shown in Example 1. For this multivariate t-distribution with the degrees of freedom 5, the variances of all predictors are equal to 1. The true coefficient vector β⁰ is the same as the vector shown in Example 1. The true model is $Y=\mathbf{X}{\beta }^0+\mathit{ϵ}$, where the errors ϵ₁, ϵ₂, . . ., ϵ_n follow the Student’s t-distribution with degrees of freedom 10.

Example 4:

The predictors ${\left(x_{i1},\dots ,x_{ip}\right)}^T$ ∼ the mixture distribution $\rho \cdot N(\mathbf{0},10\mathbf{I})+(1-\rho )\cdot N(\mathbf{0},0.5\mathbf{I})$, where ρ = 0.03 and I is a p × p identity matrix. The true coefficient vector β⁰ is the same as the vector shown in Example 1. The true model is $Y=\mathbf{X}{\beta }^0+\mathit{ϵ}$, where the errors ϵ₁, ϵ₂, . . ., ϵ_n follow the Skew-t distribution (Azzalini (2013)) with degrees of freedom 4.

For each example, we repeated the simulation 30 times. To evaluate different methods, we use the following five measures: ${\ell }_2$ distance ${\Vert \widehat{\beta }-{\beta }^0\Vert }_2$, mean squared error (MSE), false positive rate (FPR), false negative rate (FNR), and the elapsed time (in seconds) using R. Tables 1 and 2 show the performance comparison of different methods in the Gaussian case and the heavy-tailed case, respectively. The results indicate that our proposed methods deliver the best performance on all these four examples. For the Gaussian case shown in Table 1, DISCOM delivers better performance than the DISCOM-Huber method. For the heavy-tailed case shown in Table 2, DISCOM-Huber performs better. These numerical results are consistent with our theoretical studies shown in Section 3.

Table 1:

Performance comparison for the Gaussian case.

Methods	Example 1					Example 2
	${\Vert \widehat{\beta }-{\beta }^0\Vert }_2$	MSE	FPR	FNR	TIME	${\Vert \widehat{\beta }-{\beta }^0\Vert }_2$	MSE	FPR	FNR	TIME
Lasso	0.655 (0.026)	1.431 (0.045)	0.069 (0.004)	0.015 (0.009)	0.016 (0.000)	0.920 (0.025)	1.988 (0.059)	0.133 (0.007)	0.002 (0.002)	0.019 (0.004)
Imputed-Lasso	0.674 (0.017)	1.338 (0.018)	0.076 (0.007)	0.004 (0.004)	0.802 (0.006)	0.690 (0.013)	1.546 (0.030)	0.122 (0.007)	0.000 (0.000)	1.099 (0.008)
Ridge	1.270 (0.004)	3.962 (0.062)	1.000 (0.000)	0.000 (0.000)	0.025 (0.000)	1.662 (0.006)	5.262 (0.066)	1.000 (0.000)	0.000 (0.000)	0.025 (0.000)
Imputed-Ridge	1.094 (0.013)	2.304 (0.035)	1.000 (0.000)	0.000 (0.000)	0.780 (0.006)	1.332 (0.009)	3.130 (0.048)	1.000 (0.000)	0.000 (0.000)	1.093 (0.008)
IMSF	0.585 (0.020)	1.358 (0.037)	0.173 (0.009)	0.000 (0.000)	5.554 (0.068)	0.777 (0.016)	1.730 (0.040)	0.291 (0.012)	0.000 (0.000)	5.900 (0.075)
DISCOM	0.416 (0.013)	1.133 (0.016)	0.025 (0.003)	0.000 (0.000)	13.552 (0.078)	0.600 (0.020)	1.378 (0.033)	0.074 (0.007)	0.000 (0.000)	12.391 (0.064)
DISCOM-Huber	0.434 (0.013)	1.145 (0.016)	0.026 (0.003)	0.000 (0.000)	28.618 (0.886)	0.605 (0.021)	1.380 (0.035)	0.076 (0.008)	0.000 (0.000)	25.907 0.122
Fast-DISCOM	0.465 (0.015)	1.160 (0.016)	0.039 (0.005)	0.000 (0.000)	3.600 (0.027)	0.641 (0.017)	1.438 (0.033)	0.109 (0.006)	0.000 (0.000)	3.241 (0.029)
Fast-DISCOM-Huber	0.481 (0.015)	1.173 (0.016)	0.036 (0.004)	0.000 (0.000)	16.802 (0.081)	0.655 (0.020)	1.457 (0.037)	0.100 (0.007)	0.000 (0.000)	16.767 (0.096)

[Note that the values in the parentheses are the standard errors of the measures.]

Table 2:

Performance comparison for the heavy-tailed case.

Methods	Example 3					Example 4
	${\Vert \widehat{\beta }-{\beta }^0\Vert }_2$	MSE	FPR	FNR	TIME	${\Vert \widehat{\beta }-{\beta }^0\Vert }_2$	MSE	FPR	FNR	TIME
Lasso	0.751 (0.036)	1.809 (0.055)	0.070 (0.006)	0.056 (0.017)	0.021 (0.004)	1.305 (0.029)	3.331 (0.087)	0.064 (0.007)	0.419 (0.054)	0.020 (0.005)
Imputed-Lasso	0.751 (0.023)	1.669 (0.039)	0.071 (0.008)	0.026 (0.010)	0.687 (0.010)	0.930 (0.030)	2.699 (0.073)	0.147 (0.014)	0.033 (0.016)	0.530 (0.013)
Ridge	1.294 (0.004)	4.454 (0.114)	1.000 (0.000)	0.000 (0.000)	0.028 (0.003)	1.420 (0.006)	3.548 (0.069)	1.000 (0.000)	0.000 (0.000)	0.039 (0.006)
Imputed-Ridge	1.143 (0.013)	2.731 (0.064)	1.000 (0.000)	0.000 (0.000)	0.657 (0.010)	1.326 (0.011)	3.342 (0.080)	1.000 (0.000)	0.000 (0.000)	0.527 (0.011)
IMSF	0.622 (0.025)	1.637 (0.041)	0.173 (0.013)	0.004 (0.004)	6.569 (0.297)	1.048 (0.028)	2.878 (0.083)	0.189 (0.012)	0.052 (0.017)	6.989 (0.188)
DISCOM	0.579 (0.022)	1.560 (0.038)	0.037 (0.004)	0.004 (0.004)	12.086 (0.134)	0.871 (0.025)	2.590 (0.067)	0.193 (0.017)	0.011 (0.006)	12.362 (0.153)
DISCOM-Huber	0.507 (0.017)	1.452 (0.025)	0.027 (0.003)	0.000 (0.000)	26.073 (0.104)	0.780 (0.021)	2.468 (0.054)	0.137 (0.012)	0.004 (0.004)	26.925 (0.228)
Fast-DISCOM	0.601 (0.022)	1.604 (0.047)	0.040 (0.004)	0.004 (0.004)	3.317 (0.041)	1.151 (0.025)	3.028 (0.079)	0.207 (0.019)	0.085 (0.033)	3.626 (0.050)
Fast-DISCOM-Huber	0.561 (0.021)	1.496 (0.031)	0.035 (0.004)	0.000 (0.000)	17.835 (0.079)	0.786 (0.022)	2.482 (0.055)	0.137 (0.013)	0.000 (0.000)	17.042 (0.134)

[Note that the values in the parentheses are the standard errors of the measures.]

In addition, as shown in Tables 1 and 2, for the Lasso and ridge regression, using the imputed data can improve performance in most cases. However, as shown in Table 1, the Lasso method using the imputed data may deliver worse estimate of the true coefficient vector β⁰, possibly due to the block-missing pattern. Compared with the Lasso and Ridge regression methods using the imputed data set or only the samples with complete observations, the IMSF method delivers better estimation and prediction. On the other hand, IMSF method has high false positive rates for all four simulated examples. The comparison between IMSF and our proposed DISCOM and DISCOM-Huber shows that our proposed methods could use all available data more effectively and therefore acquires better performance.

For each simulation of the four examples, our proposed Fast-DISCOM method using the fast tuning parameter selection method uses only 4 seconds while our original DISCOM method uses about 13 seconds. The Fast-DISCOM method is also faster than the IMSF method which uses about 7 seconds for each simulation. On the other hand, we can observe that the computing times of our original DISCOM and DISCOM-Huber methods are still acceptable. For the examples 1 and 2 generated from the Gaussian distribution, although the Fast-DISCOM method does not perform as well as the DISCOM method, it has better estimation, prediction, and model selection performance than the Lasso, ridge regression and IMSF methods. Similarly, for the examples 3 and 4 generated from the heavy-tailed distributions, although the Fast-DISCOM-Huber method does not perform as well as the DISCOM-Huber method, it also has better performance than the Lasso, ridge regression and IMSF methods. These simulation results indicate that our proposed new tuning parameter selection method accelerates the computational speed without sacrificing the estimation, prediction, and model selection performance too much.

5. Real Data Analysis

In this section, we show the analysis of the Alzheimer’s Disease Neuroimaging Initiative (ADNI) data as an application example. The main goal of ADNI is to test whether serial magnetic resonance imaging (MRI), positron emission tomography (PET), and some other biological markers and neuropsychological assessments can be combined to measure the progression of mild cognitive impairment (MCI) and early Alzheimer’s disease (AD). In our study, we extracted features from three modalities: structural MRI, fluorodeoxyglucose PET, and CerebroSpinal Fluid (CSF). Imaging preprocessing was performed for MRI and PET images. For the MRI, after some correction, spatial segmentation, and registration steps, we obtained the subject lableled image based on the Jacob template (Kabani et al. (1998)) with 93 manually labeled regions of interest (ROI). For each of the 93 ROIs in the labeled MRI, we computed the volume of gray matter as a feature. For each PET image, we first aligned the PET image to its respective MRI using affine registration. Then, we calculated the average intensity of every ROI in the PET image as a feature. Therefore, for each ROI, we have one MRI feature and one PET feature. For the CSF modality, five biomarkers were used in this study, namely amyloid β (Aβ42), CSF total tau (t-tau), tau hyperphosphorylated at threonine 181 (p-tau), and two tau ratios with respective to Aβ42 (i.e., t-tau/Aβ42 and p-tau/Aβ42).

After data processing, we got 93 features from MRI, 93 features from PET, and 5 features from CSF. There are 805 subjects in total, including 1) 199 subjects with complete MRI, PET, and CSF features, 2) 197 subjects with only MRI and PET features, 3) 201 subjects with only MRI and CSF features, and 4) 208 subjects with only MRI features. The response variable used in our study is the Mini Mental State Examination (MMSE) score. As a brief 30-point questionnaire test, MMSE can be used to examine a patient’s arithmetic, memory and orientation (Folstein et al. (1975)). It is very useful to help evaluate the stage of AD pathology and predict future progression. We will use all available data from MRI, PET, and CSF to predict the MMSE score.

In our analysis, we divided the data into three parts: training data set, tuning data set, and testing data set. The training data set consists of all subjects with incomplete observations and 40 randomly selected subjects with complete MRI, PET, and CSF features. The tuning data set consists of another 40 randomly selected subjects (different from the training data set) with complete observations. The testing data set contains the other 119 subjects with complete observations. The tuning data set was used to choose the best tuning parameters for all methods and the testing data set was used to evaluate different methods. We used all methods shown in the simulation study to predict the MMSE score. For each method, the analysis was repeated 30 times using different partitions of the data.

The results in Table 3 show that our proposed Fast-DISCOM-Huber method acquires the best prediction performance. All our proposed DISCOM methods deliver better performance than the Lasso, Ridge, and IMSF methods. The IMSF method has better prediction performance than the Lasso and ridge regression using only samples with complete observations. However, IMSF does not perform as well as the ridge regression using the imputed data. Regarding the model selection, since the number of variables selected by the Lasso is at most the sample size (Zou and Hastie (2005)), as shown in Table 3, the Lasso method using the imputed data selected many more features than the method using only samples with complete observations. Both IMSF and our proposed methods could deliver a model with relatively small numbers of features.

Table 3:

Performance comparison for the ADNI data.

Methods	MSE		Number of Features		TIME
	Mean	SE	Mean	SE	Mean	SE
Lasso	5.711	0.341	11.733	1.638	0.009	0.002
Imputed-Lasso	4.711	0.082	86.700	8.559	0.559	0.017
Ridge	5.273	0.204	191.000	0.000	0.010	0.000
Imputed-Ridge	4.478	0.055	191.000	0.000	0.177	0.006
IMSF	4.630	0.079	28.400	3.025	2.960	0.073
DISCOM	4.285	0.068	27.933	2.261	4.675	0.028
DISCOM-Huber	4.161	0.059	23.100	0.846	10.348	0.025
Fast-DISCOM	4.146	0.055	28.100	0.809	1.565	0.007
Fast-DISCOM-Huber	4.123	0.069	25.833	1.311	8.012	0.019

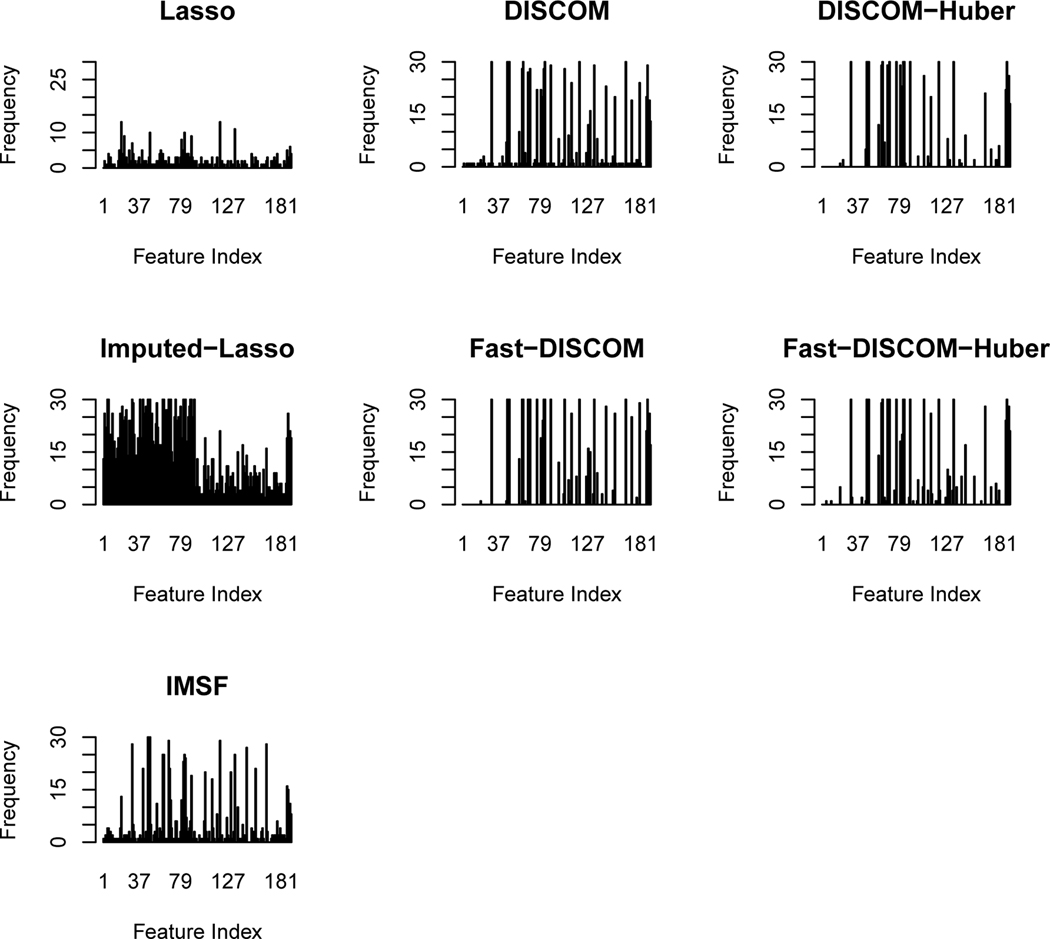
Figure 2 shows the selection frequency of all the 191 features. The selection frequency of each feature is defined as the times of being selected in the 30 times replications. As shown in Figure 2, for our proposed DISCOM methods, some features were always selected and many features were never selected in the 30 times replications. This means that our method could deliver relatively robust performance on model selection. However, for some other methods such as the Imputed-Lasso method, they selected very different features in different replications and therefore many features have positive and low selection frequencies. For the Imputed-Lasso method, one possible reason for the unstable performance on model selection is due to the randomness involved in the imputation of a lot of block-missing data.

Figure 2:

Selection frequency of 191 features for the prediction of MMSE score.

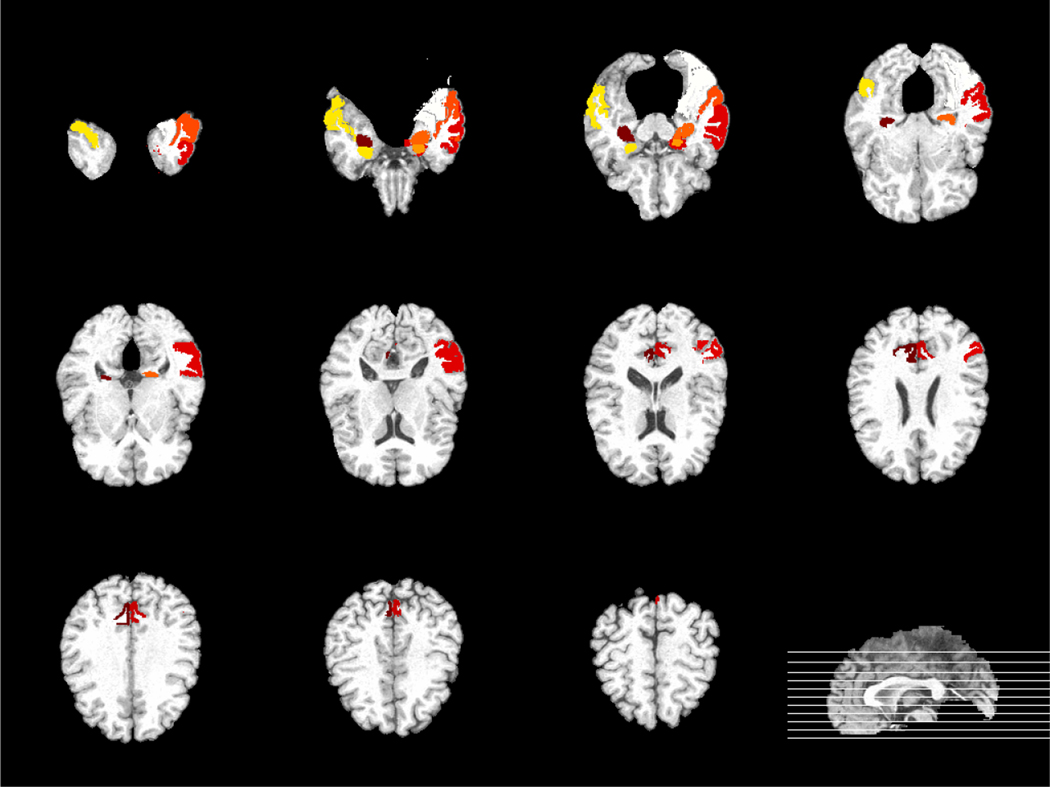
To further understand our results, since each MRI feature and each PET feature are corresponding to one ROI, we can examine whether the selected features are meaningful by studying their corresponding brain regions. In our 30 times of experiments using different random splits, there are 9 MRI features and 2 PET features always selected by our proposed DISCOM-Huber and Fast-DISCOM-Huber methods. Figure 3 shows the multi-slice view of the brain regions (regions with color) corresponding to these 11 features. Among these 11 brain regions, some regions such as hippocampal formation right (30-th region), uncus left (46-th region), middle temporal gyrus left (48-th region), hippocampus formation left (69-th region) and amygdale right (83-th region), are known to be highly correlated with AD and MCI by many studies using group comparison methods (Misra et al. (2009); Zhang and Shen (2012)). It would be interesting to study whether the other six always selected brain regions are truly related with AD by some scientific experiments.

Figure 3:

The multi-slice view of the brain regions always selected by DISCOM-Huber and Fast-DISCOM-Huber.

In addition, as shown in Table 3, all our proposed DISCOM methods solve this real data analysis problem with 191 features within 11 seconds. This indicates that the time cost of our methods is not very expensive. In summary, our real data analysis indicates that our proposed method can solve practical problems well.

6. Conclusion

In this paper, we propose a new two-step procedure to find the optimal linear prediction of a continuous response variable using the block-missing multi-modality predictors. In the first step, we estimate the covariance matrix of the predictors using a linear combination of the identity matrix, and the estimates of the intra-modality covariance matrix and the cross-modality covariance matrix. The proposed estimator of the covariance matrix can be positive semi-definite and more accurate than the sample covariance matrix. We also use all available information to estimate the cross covariance vector between the predictors and the response variable. Robust estimate based on the Huber’s M-estimate is also proposed for the heavy-tailed case. In the second step, based on the estimated covariance matrix and the cross-covariance vector, a modified Lasso estimator is used to deliver a sparse estimate of the coefficients in the optimal linear prediction. The effectiveness of the proposed method is demonstrated by both theoretical and numerical studies. The comparison between our proposed method and several existing ones also indicates that our method has promising performance on estimation, prediction, and model selection for the block-missing multi-modality data.