Abstract
To significantly increase the amount of exsolved particles, the complete phase reconstruction from simple perovskite to Ruddlesden-Popper (R-P) perovskite is greatly desirable. However, a comprehensive understanding of key parameters affecting the phase reconstruction to R-P perovskite is still unexplored. Herein, we propose the Gibbs free energy for oxygen vacancy formation in Pr0.5(Ba/Sr)0.5TO3-δ (T = Mn, Fe, Co, and Ni) as the important factor in determining the type of phase reconstruction. Furthermore, using in-situ temperature & environment-controlled X-ray diffraction measurements, we report the phase diagram and optimum ‘x’ range required for the complete phase reconstruction to R-P perovskite in Pr0.5Ba0.5-xSrxFeO3-δ system. Among the Pr0.5Ba0.5-xSrxFeO3-δ, (Pr0.5Ba0.2Sr0.3)2FeO4+δ – Fe metal demonstrates the smallest size of exsolved Fe metal particles when the phase reconstruction occurs under reducing condition. The exsolved nano-Fe metal particles exhibit high particle density and are well-distributed on the perovskite surface, showing great catalytic activity in fuel cell and syngas production.
Subject terms: Energy, Fuel cells, Fuel cells
The complete phase reconstruction to Ruddlesden-Popper perovskite is greatly desirable to increase the exsolved particle distribution. Here, the authors report a key factor for the complete phase reconstruction in perovskites, leading to good catalytic activity in fuel cell and syngas production.
Introduction
Tailoring the functionality of perovskite oxides (ABO3) by decorating the surface with catalytically active particles plays an important role in energy-related applications such as fuel cells, electrolysis cells, metal-air batteries, and supercapacitors1–6. The catalyst particles are typically prepared by deposition techniques (e.g. infiltration, chemical vapor deposition, and pulsed laser deposition), in which the catalysts are embedded onto the surface from external precursors7–9. However, these techniques require redundant heat-treatments for preparation and the catalyst particles suffer from agglomeration and/or coarsening over time, resulting in performance degradation10,11. In this respect, it is of great importance to develop more robust and time-efficient catalyst preparation method. Exsolution phenomenon on the basis of in-situ growth of metal particles has been suggested as an advanced approach to designing perovskite matrix with electro-catalytically active particles12,13. In this approach, catalytically-active metal elements (e.g. Pd, Ru, Co, Ni, and Fe, etc…) are initially incorporated into the B-site of perovskite oxides, and then exsolved as metallic particles from the perovskite support under reducing atmosphere14,15. As compared with the conventional catalyst preparation methods, the in-situ exsolution process provides benefits of time-efficient catalyst preparation, enhanced catalyst lifetime, and robust thermal stability16,17. Notwithstanding the advantages, two major thresholds hinder the practical application of the exsolution process: (i) restricted diffusion of catalytically active cations to the surface due to preferential segregation within the bulk18, and (ii) structural destruction and/or insulating phase evolution after excessive cation defect formation19.
In order to address the challenges of the exsolution phenomenon, A-site deficient perovskites (A/B < 1) has been extensively employed as an attractive methodology2,20–22. In A-site deficient perovskites, formation of oxygen vacancies is promoted by phase stabilization from non-stoichiometric perovskite to defect-free perovskite under reducing condition, facilitating the B-site exsolution23,24. Hence, the B-site exsolution level is proportional to A-site deficiency range (‘α ’ for A1-αBO3−δ). Meanwhile, there exists restriction in the variation of A-site deficiency range (about 0 < α < 0.2 for A1-αBO3−δ) because excessive A-site deficiency may be accompanied by formation of undesirable A-site oxide phases19,25. Given these aspects, an alternative corresponding method to further trigger the B-site exsolution is using the in-situ phase reconstruction from simple perovskite to Ruddlesden-Popper (R-P) perovskite oxides (An+1BnO3n+1 with n = 1, 2, and 3) via reduction process26,27. This strategy facilitates abundant formation of oxygen vacancies during the phase reconstruction, breaking the bottleneck of exsolution capability.
| 1 |
From Eq. 1, it is presumable that considerable number of cations at B-site will be reduced into metals without A-site segregation after phase reconstruction from simple perovskite (ABO3) to n = 1 R-P perovskite (A2BO4). Although several perovskites have exhibited superior distribution of catalyst particles on the surface via phase transition to R-P perovskite28–30, the comprehensive understanding of key factors modulating the phase reconstruction to R-P perovskite is still an open question.
Inspired by the above perspectives, the goal of this study is to identify the significant factor contributing to the phase reconstruction from simple perovskite to R-P perovskite. Here, we systematically report the Gibbs free energy for oxygen vacancy formation (Gvf-O) of perovskite oxides with various cations as the unprecedented factor affecting the phase reconstruction. The type of phase reconstruction could be predicted with the Gvf-O value from PrO and TO2 networks in Pr0.5(Ba/Sr)0.5TO3−δ (T = Mn, Fe, Co, and Ni), in which the most appropriate cations for the complete reconstruction to R-P perovskite are determined. Afterwards, the phase diagram from in-situ temperature and environment-controlled X-ray diffraction (XRD) measurements reveals the phase reconstruction tendency of Pr0.5Ba0.5−xSrxFeO3−δ (x = 0, 0.1, 0.2, 0.3, 0.4, and 0.5, abbreviated as PBSF in Supplementary Table 1) materials with respect to ‘x’ value and reduction temperature. Furthermore, the as-exsolved Fe metal particle size and distribution for PBSF after reduction process are observed from microscopy analysis. In accordance with the theoretical calculations and experimental data, Pr0.5Ba0.2Sr0.3FeO3−δ (A-PBSF30) is adopted as the optimized electrode material for symmetrical solid oxide cell (S-SOC) and demonstrates exceptional electrochemical performance (1.23 W cm−2 at 800 °C under fuel cell mode and −1.62 A cm−2 at 800 °C under co-electrolysis mode).
Results
Density functional theory calculations
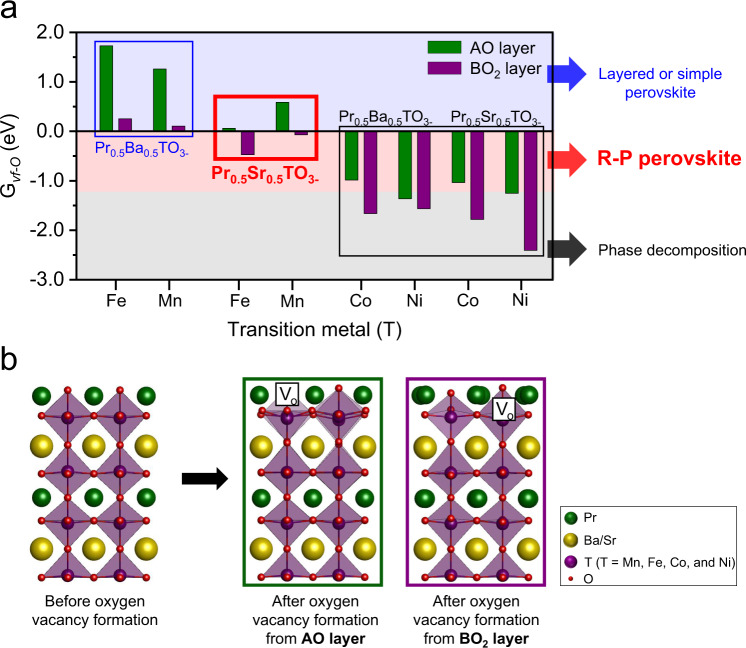
The complete phase reconstruction from simple perovskite (ABO3) to R-P perovskite (A2BO4) via reduction is considered as one of the efficient strategies to significantly boost the population of exsolved particles. However, the key factors contributing to the phase reconstruction to R-P perovskite has not been investigated. To determine the unexplored factor for the phase reconstruction for the first time, the Gibbs free energy for oxygen vacancy formation (Gvf-O) and the oxygen vacancy formation energies (Evf-O) from the surface AO (A-site) and BO2 (B-site) networks were calculated for Pr0.5Ba0.5TO3−δ and Pr0.5Sr0.5TO3−δ (T = Mn, Fe, Co, and Ni) perovskite oxides (Fig. 1 and Supplementary Fig. 1)31–34. For the perovskite oxides to undergo phase reconstruction without phase decomposition under reducing condition, the A-site Gvf-O value should be positive (A-site Gvf-O > 0 eV). Moreover, the B-site Gvf-O value would be an important factor for determining the type of phase reconstruction. For instance, the B-site Gvf-O should be in the range of about −1.2 to 0 eV (−1.2 eV < B-site Gvf-O < 0 eV) to demonstrate complete phase reconstruction to R-P perovskite in the reduction environment. Considering the aforementioned results and the experimental data, only Pr0.5Sr0.5MnO3−δ (PSM) and Pr0.5Sr0.5FeO3−δ (A-PBSF50) are the possible candidates for the complete phase reconstruction to R-P perovskite in this study (Supplementary Fig. 2). Among the two potential candidates, we adopted Fe cation as the more suitable B-site cation because of its much superior catalytic activity for fuel oxidation reaction rather than Mn cation18. Accordingly, we systematically analyzed the phase reconstruction tendency of Pr0.5Ba0.5−xSrxFeO3−δ (x = 0, 0.1, 0.2, 0.3, 0.4, and 0.5, abbreviated as PBSF in Supplementary Table 1) materials with respect to different Ba2+/Sr2+ ratio.
Fig. 1. Density functional theory calculations.
a Calculated Gibbs free energy for oxygen vacancy formation (Gvf-O) of Pr0.5(Ba/Sr)0.5TO3−δ (T = Mn, Fe, Co, and Ni) from the surface AO (green bar) and BO2 (purple bar) networks and the predicted phase change under reducing condition. b Schematic illustration of the most stable structure configurations of Pr0.5(Ba/Sr)0.5TO3−δ (T = Mn, Fe, Co, and Ni) slab models used for the calculations of oxygen vacancy formation energy values from AO and BO2 networks.
Structural characterization
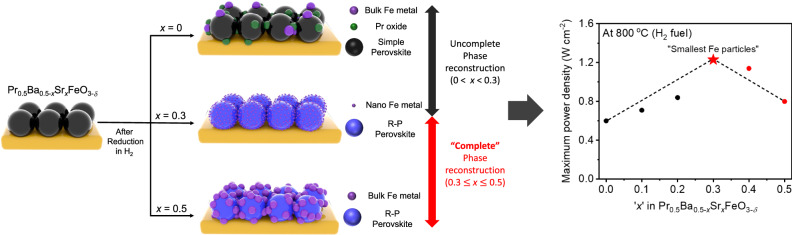
Before examining the phase reconstruction tendency of PBSF, the crystalline structures after heat-treated in two different environmental conditions were analyzed by X-ray diffraction (XRD) and Rietveld refinement profiles (Supplementary Figs. 3, 4 and Supplementary Table 2). The air-sintered PBSF are all corresponded to simple perovskite structure without detectable secondary phases. On the other hand, after reduction in H2 atmosphere, the PBSF samples were surprisingly changed to different types of phases depending on the Sr2+ concentration. As shown in Supplementary Fig. 4b, Pr0.5Ba0.5FeO3−δ (A-PBSF00), Pr0.5Ba0.2Sr0.3FeO3−δ (A-PBSF30), and Pr0.5Sr0.5FeO3−δ (A-PBSF50) were changed to Pr0.5Ba0.5FeO3−δ – Fe metal & Pr oxide (R-PBSF00), (Pr0.5Ba0.2Sr0.3)2FeO4+δ – Fe metal (R-PBSF30), and (Pr0.5Sr0.5)2FeO4+δ – Fe metal (R-PBSF50), respectively. Only catalytically active Fe metal peaks along with complete phase reconstruction to R-P perovskite are observed for R-PBSF30 and R-PBSF50, while R-PBSF00 shows Fe metal and Pr oxide segregation without phase reconstruction under reducing condition. Based on the further Rietveld refinement analysis in Supplementary Fig. 5, R-PBSF30 clearly exhibits the complete phase reconstruction to R-P perovskite with tetragonal structure (space group I4/mmm with lattice parameters of a = b = 3.879 and c = 12.704 Å). The complete phase reconstruction could be also described by Eq. (2), of which considerable amounts of Fe metal are expected to be exsolved in the reduction environment.
| 2 |
Phase reconstruction tendency analysis from phase diagram
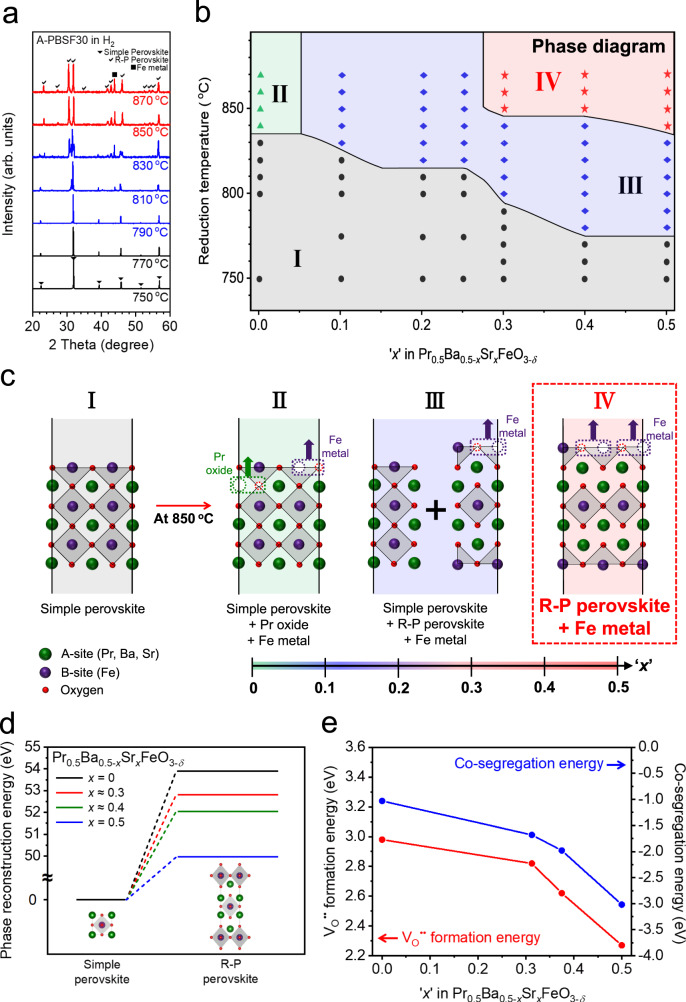
To precisely analyze the phase reconstruction tendency for Pr0.5Ba0.5−xSrxFeO3−δ (x = 0, 0.1, 0.2, 0.25, 0.3, 0.4, and 0.5) materials, in-situ XRD measurements were systematically conducted in various reduction temperatures and Sr2+ concentrations. (Fig. 2a and Supplementary Fig. 6). Figure 2b displays the proposed phase diagram and the corresponding plotted points after in-situ XRD measurements in H2 with elevating temperature intervals of 10 °C. The A-PBSF00 sample remained simple perovskite structure for all reduction temperature range and co-segregation of Fe metal and Pr oxide was observed simultaneously at the reduction temperature higher than 840 °C (Region II in Fig. 2b). Even though there was noticeable phase reconstruction for all Sr2+-doped samples, complete phase reconstruction to R-P perovskite was not accomplished for Pr0.5Ba0.4Sr0.1FeO3−δ (A-PBSF10), Pr0.5Ba0.3Sr0.2FeO3−δ (A-PBSF20), and Pr0.5Ba0.25Sr0.25FeO3−δ (A-PBSF25) even at the reduction temperature of 870 °C. (Region III in Fig. 2b). On the contrary, complete phase reconstruction to R-P perovskite is observed for A-PBSF30, Pr0.5Ba0.1Sr0.4FeO3−δ (A-PBSF40), and A-PBSF50 at the reduction temperature of approximately 850 °C (Region IV in Fig. 2b). These results indicate that the ‘x’ value in PBSF should be at least approximately 0.3 along with the reduction temperature of about 850 °C to accomplish complete phase reconstruction, as illustrated in Fig. 2c.
Fig. 2. Examination of phase reconstruction behavior for Pr0.5Ba0.5−xSrxFeO3−δ material under reducing condition.
a–c Phase reconstruction tendency of Pr0.5Ba0.5−xSrxFeO3−δ material (x = 0, 0.1, 0.2, 0.25, 0.3, 0.4, and 0.5). a In-situ powder X-ray diffraction (XRD) patterns of Pr0.5Ba0.2Sr0.3FeO3−δ (A-PBSF30) under H2 environment. b Proposed phase diagram of Pr0.5Ba0.5−xSrxFeO3−δ material (x = 0, 0.1, 0.2, 0.25, 0.3, 0.4, and 0.5) in H2 environment as functions of reduction temperature and Sr2+ concentration from in-situ XRD measurements. The phases for region I (gray), II (green), III (blue), and IV (red) are simple perovskite, simple perovskite + Pr oxide + Fe metal, simple perovskite + Ruddlesden-Popper (R-P) perovskite + Fe metal, and R-P perovskite + Fe metal, respectively. c Schematic illustration of the above phase diagram. d, e Density functional theory (DFT) calculations. Calculated profiles of d the relative total energy required for the phase reconstruction from simple perovskite to R-P perovskite and e oxygen vacancy formation energies and co-segregation energies as a function of Sr2+ concentration in four models.
Effect of Sr2+ concentration on phase reconstruction and exsolution
The role of Sr2+ concentration in PBSF in terms of phase reconstruction tendency to R-P perovskite was additionally explored using density functional theory (DFT) calculations. Figure 2d shows the required total energies for the phase reconstruction (Erecon) from simple perovskite to R-P perovskite of four model structures with different Ba2+/Sr2+ ratio. The Erecon decreases with increasing Sr2+ concentration in PBSF, indicating that the incorporation of Sr2+ into Ba2+ site promotes the phase reconstruction to R-P perovskite (Supplementary Fig. 7). Furthermore, the Evf-O of four simple perovskite models were calculated in Fig. 2e. More negative Evf-O value implies easier formation of oxygen vacancies in the reduction environment35. The Evf-O value becomes more negative after doping Sr2+ into Ba2+, revealing that the Sr2+ doping facilitates the formation of oxygen vacancies in the reduction atmosphere. This trend could be elucidated by the decrease in tolerance factor after replacement of Ba2+ by Sr2+ (Supplementary Table 3)36. A co-segregation energy (Eco-seg) associated to the degree of exsolution for B-site transition metal cations under reducing condition was also calculated (Fig. 2e). Interestingly, Eco-seg decreased as the Sr2+ contents increased, suggesting the enhanced degree of Fe exsolution with increasing Sr2+ concentration.
Transmission electron microscopy analysis
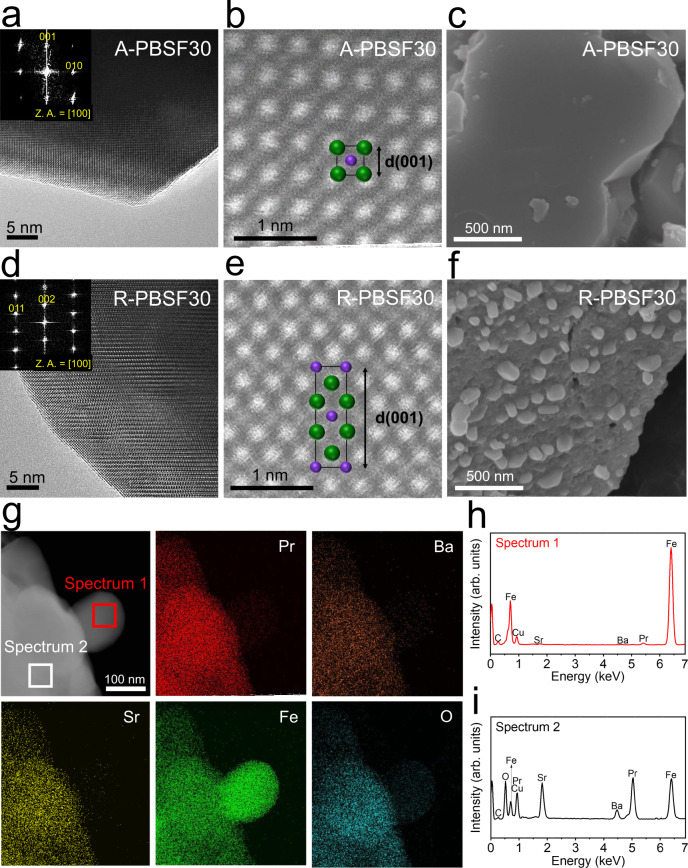
On the basis of proposed phase diagram and DFT calculations, the A-PBSF30, the minimum Sr2+-doped sample demonstrating complete reconstruction to R-P perovskite, is selected as the target material for structural analysis. The transmission electron microscopy (TEM) and scanning TEM (STEM) analysis were successfully performed to visually probe the complete phase reconstruction from simple perovskite to R-P perovskite of A-PBSF30 material (Fig. 3 and Supplementary Fig. 8). From the high-resolution TEM images and corresponding fast-Fourier transformed (FFT) patterns, the lattice spaces between planes of A-PBSF30 and R-PBSF30 are 0.395 nm (Fig. 3a) and 0.634 nm (Fig. 3d), which are consistent with the lattice constant of (001) plane for simple perovskite and the lattice constant of (002) plane for R-P perovskite, respectively. Furthermore, the atomic-scale observations of A-PBSF30 and R-PBSF30 were definitely validated from high-angle annular dark-field (HAADF) STEM images, of which only technically elusive [100] direction is mandatory for R-P perovskite. The locations of cations are well-matched with the simple perovskite (Fig. 3b) and R-P perovskite (Fig. 3e) because the atomic column intensity is proportional to the Z~2 (Z is the atomic number)37, thereby the bright and dark columns are the A-site (i.e., Pr, Ba, and Sr (green)) and the B-site (i.e., Fe (purple)), respectively, in the HAADF-STEM mode.
Fig. 3. Electron microscopic analysis.
a, b, d, e Transmission electron microscopy (TEM) analysis. a High-resolution (HR) TEM image and the corresponding fast-Fourier transformed (FFT) pattern of Pr0.5Ba0.2Sr0.3FeO3−δ (A-PBSF30) with zone axis (Z.A.) = [100] and b high-angle annular dark-field (HAADF) scanning TEM (STEM) image of A-PBSF30 with simple perovskite structure of [100] direction with d-spacing 001. d HR TEM image and the corresponding FFT pattern of (Pr0.5Ba0.2Sr0.3)2FeO4+δ – Fe metal (R-PBSF30) with Z.A. = [100] and e HAADF STEM image and the atomic arrangement of R-PBSF30 of [100] direction with d-spacing 001. c, f Scanning electron microscope (SEM) images. SEM images presenting the surface morphologies of c A-PBSF30 sintered at 1200 °C for 4 h in air atmosphere and f R-PBSF30 reduced at 850 °C for 4 h in humidified H2 environment (3% H2O). g–i Scanning TEM-energy dispersive spectroscopy (EDS) analysis. g HAADF image of R-PBSF30 and elemental mapping of Pr, Ba, Sr, Fe, and O, respectively. h, i EDS spectra of h the exsolved Fe metal particle (Spectrum 1, red) and i the parent material (Pr0.5Ba0.2Sr0.3)2FeO4+δ (Spectrum 2, black).
Examination and characterization of exsolved particle size
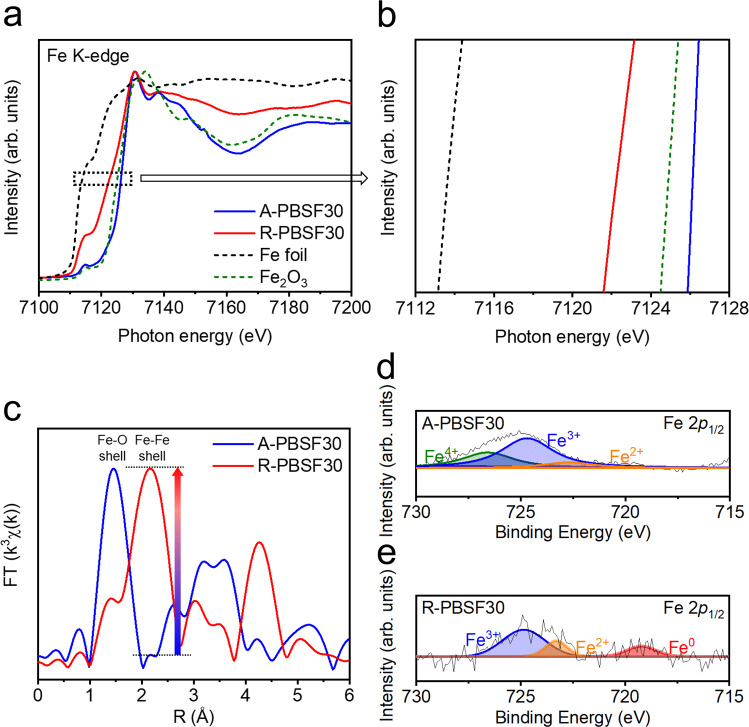
In general, particle size and surface distribution of catalysts have a considerable influence on the catalytic activity4,38. As such, the particle size and surface distribution of exsolved metal particles via reduction treatment could impact on the electro-catalytic activity of catalysts. Before examining the electro-catalytic effect of the in-situ exsolved Fe metal particles, an explicit comparison of exsolved particle size and surface distribution for R-PBSF00, R-PBSF30, and R-PBSF50 samples were presented in scanning electron microscope (SEM) images (Fig. 3c, f and Supplementary Figs. 9, 10). As shown in Fig. 3f, many small particles with size of about 100 to 200 nm are observed and uniformly socketed onto the perovskite oxide matrix after reduction, which are speculated as Fe metal particles. In contrast, the size of exsolved particles was relatively larger for R-PBSF00 and R-PBSF50 (Supplementary Figs. 11, 12). The energy dispersive spectroscopy (EDS) spectrum and the elemental mapping images of R-PBSF30 also clearly revealed that Fe metal particle with size of about 150 nm is well-socketed onto the R-P perovskite after reduction (Fig. 3g, h). Furthermore, noticeable energy shift to the higher energy in X-ray absorption near-edge structure (XANES), much increase in Fe-Fe shell intensity from the Fourier-transformed extended X-ray absorption fine structure (EXAFS) spectra after reduction, and the presence of Fe0 2p1/2 peak for only R-PBSF30 from X-ray photoelectron spectroscopy (XPS) measurements confirm the exsolution of Fe metal onto the surface under reducing condition39, in coincidence with the above experimental results (Fig. 4). To investigate the electrically conductive properties of the exsolved Fe metal particles, the electrical conductivities as a function of temperature under reducing atmosphere were measured for PBSF (Supplementary Fig. 13). The A-PBSF30 displayed the highest electrical conductivity value compared to other PBSF in the reduction environment coupled with sufficiently high electrical conductivity in the air atmosphere (Supplementary Fig. 13b)40, suggesting that the A-PBSF30 is the potential electrode material for S-SOC electrode material.
Fig. 4. Oxidation state characterization.
a, b Fe K-edge X-ray absorption near-edge structure (XANES) spectra of Pr0.5Ba0.2Sr0.3FeO3−δ (A-PBSF30), (Pr0.5Ba0.2Sr0.3)2FeO4+δ (R-PBSF30) with two references (Fe foil and Fe2O3). c Fourier-transformed Fe K-edge extended X-ray absorption fine structure (EXAFS) spectra of A-PBSF30 and R-PBSF30. X-ray photoelectron spectra (XPS) of Fe 2p1/2 for d A-PBSF30 and e R-PBSF30.
Electrochemical performance evaluation
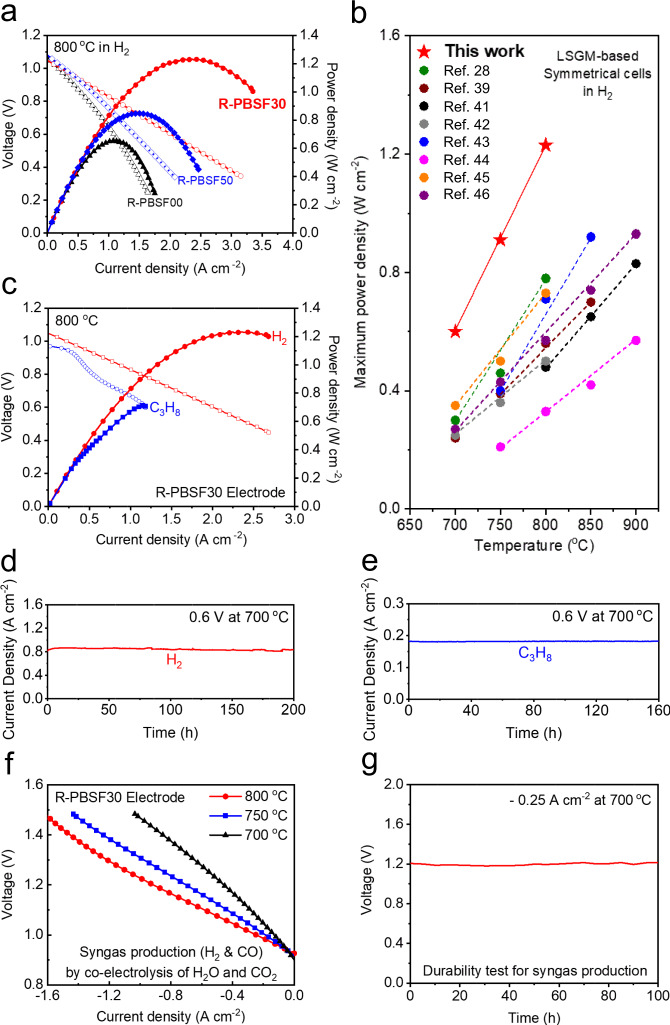
Prior to assessment of electrochemical performance for A-PBSF30 in the practical application of S-SOCs, great thermo-chemical compatibility between all PBSF and the La0.9Sr0.1Ga0.8Mg0.2O3−δ (LSGM) electrolyte was confirmed by XRD measurement (Supplementary Fig. 14). Moreover, similar microstructures of air-sintered PBSF samples imply that the electrochemical performance would not be affected by surface morphology (Supplementary Fig. 15). Then, electrochemical performance of symmetrical solid oxide fuel cells (S-SOFCs) using PBSF as both electrodes was characterized by LSGM electrolyte-supported cells to identify the huge impact of the exsolved Fe metal particle size and surface distribution (Fig. 5a and Supplementary Figs. 16, 17). The peak power density of the A-PBSF30 symmetrical cell is 1.23 W cm−2 at 800 °C with humidified H2 (3% H2O) as fuel. This outstanding cell performance is the highest out of open literature based on LSGM electrolyte-supported S-SOFCs without any external catalysts at 800 °C under humidified H2 (3% H2O) as fuel to our best knowledge (Fig. 5b and Table 1)28,39,41–46. In addition, peak power output of 0.73 W cm−2 was demonstrated in humidified C3H8 (3% H2O) at 800 °C (Fig. 5c and Supplementary Fig. 18). Furthermore, the A-PBSF30 symmetrical cell demonstrated fairly stable current density without observable degradation for about 200 h in H2 and 150 h in C3H8 at 700oC (Fig. 5d, e). We also evaluated the electrochemical performance of the A-PBSF30 symmetrical cell in co-electrolysis mode. The excellent current density of −1.62 A cm−2 at a cell voltage of 1.5 V (close to thermo-neutral voltage)47 at 800 °C under co-electrolysis condition was demonstrated for the A-PBSF30 symmetrical cell (Fig. 5f), which is exceptionally high compared to other oxygen-conducting solid oxide electrolysis cell (SOEC) systems with different electrode materials19,31,48,49. The in-operando quantitative analysis of the synthetic gas products (H2 and CO) was further investigated via gas chromatography (GC) profiles for the A-PBSF30 symmetrical cell at 800 °C during co-electrolysis of H2O and CO2 (Supplementary Fig. 19). The amount of generated H2 and CO were measured to be 0.50 and 10.81 ml min−1 cm−2, respectively, implying that the A-PBSF30 symmetrical cell could efficiently produce synthetic gas during co-electrolysis50. Together with superior electrochemical performance and efficient synthetic gas production, relatively constant voltage was observed for 100 h under a constant current load of −0.25 A cm−2 at 700 °C in co-electrolysis mode (Fig. 5g), representing great durability in continuous SOEC operation. It is noteworthy that in-situ exsolution of well-dispersed Fe metal particles after complete phase reconstruction to R-P perovskite matrix acts as catalysts with promising electro-catalytic activity (Fig. 6), leading to outstanding electrochemical performances in various applications.
Fig. 5. Electrochemical performance measurements.
a, b Comparison of the maximum power density values at 800 °C in H2. (a) in terms of Pr0.5Ba0.5−xSrxFeO3−δ compositions (x = 0, 0.3, and 0.5) and b of the present work and other LSGM electrolyte-supported studies with symmetrical cell configuration at various temperature regimes. c I–V curves and the corresponding power densities of symmetrical cell with (Pr0.5Ba0.2Sr0.3)2FeO4+δ – Fe metal (R-PBSF30) fuel electrode at 800 °C under H2 and C3H8 humidified fuels (3% H2O) fed on the fuel electrode and air fed on the air electrode. d, e Durability test of symmetrical cell with R-PBSF30 fuel electrode recorded with respect to time at a constant voltage of 0.6 V at 700 °C under d H2 and e C3H8 humidified fuels. f I–V curves for symmetrical cell with R-PBSF30 fuel electrode with humidified H2 and CO2 with H2O co-fed to the fuel electrode side and air fed to the air electrode. g Durability test of symmetrical cell with R-PBSF30 fuel electrode recorded at a constant current of −0.25 A cm−2 at 700 °C during co-electrolysis for 100 h.
Table 1.
Comparison of the electrochemical performance of La1-xSrxGa1-yMgyO3−δ (LSGM) electrolyte-supported symmetrical solid oxide fuel cells (S-SOFCs) reported in the literature and in the present study.
| Reference | Cell configuration (Air electrode | Electrolyte | Fuel electrode) | Electrolyte thickness (μm) | Maximum power density at 800 °C (W cm−2) |
|---|---|---|---|
| Present study | A-PBSF30 | LDC | LSGM | LDC | R-PBSF30 | ~250 | 1.23 |
| (28) | Pr0.4Sr0.6Co0.2Fe0.7Nb0.1O3−δ | LSGM | Pr0.8Sr1.2(Co,Fe)0.8Nb0.2O4+δ – CFA (Co-Fe alloy) | ~300 | 0.78 |
| (39) | Sr2Ti0.8Co0.2FeO6 | LSGM | Sr2Ti0.8Co0.2FeO6 | ~270 | 0.56 |
| (41) | Sr2Fe1.5Mo0.5O6-δ | LSGM | Sr2Fe1.5Mo0.5O6-δ | ~265 | 0.48 |
| (42) | Pr0.6Sr0.4Fe0.7Ni0.2Mo0.1O3−δ | GDC | LSGM | GDC | Pr0.6Sr0.4Fe0.7Ni0.2Mo0.1O3−δ | ~320 | 0.50 |
| Pr0.6Sr0.4Fe0.8Ni0.2O3−δ | GDC | LSGM | GDC | Pr0.6Sr0.4Fe0.8Ni0.2O3−δ | ~320 | 0.44 | |
| (43) | PrBa(Fe0.8Sc0.2)2O5+δ | LSGM | PrBa(Fe0.8Sc0.2)2O5+δ | ~275 | 0.71 |
| (44) | SmBaMn2O5+δ | LSGM | SmBaMn2O5+δ | ~300 | 0.33 |
| (45) | La0.5Sr0.5Fe0.9Mo0.1O3−δ | LSGM | SDC | La0.5Sr0.5Fe0.9Mo0.1O3−δ | ~300 | 0.73 |
| (46) | La0.6Sr0.4Co0.2Fe0.7Mo0.1O3−δ | SDC | LSGM | SDC | La0.6Sr0.4Co0.2Fe0.7Mo0.1O3−δ | ~270 | 0.74 |
A-PBSF30: Pr0.5Ba0.2Sr0.3FeO3−δ.
R-PBSF30: (Pr0.5Ba0.2Sr0.3)2FeO4+δ – Fe metal.
LDC: La0.4Ce0.6O2−δ.
GDC: Gd0.4Ce0.6O2−δ.
SDC: Sm0.4Ce0.6O2−δ.
LSGM: La1-xSrxGa1-yMgyO3−δ (x = 0.1 or 0.2 and y = 0.15 or 0.2).
Fig. 6. Schematic illustration of this work.
Schematic illustration of the fuel electrode side of Pr0.5Ba0.5−xSrxFeO3−δ (x = 0, 0.3, and 0.5) symmetrical cells and its relation to electrochemical performances.
Discussion
In summary, this study successfully calculated Gvf-O value from PrO and TO2 in Pr0.5(Ba/Sr)0.5TO3−δ (T = Mn, Fe, Co, and Ni) as the key factor for identifying the type of the phase reconstruction. Remarkably, the phase diagram acquired from in-situ temperature and environment-controlled XRD measurements indicated that the complete phase reconstruction to R-P perovskite occurs at least approximately x = 0.3 above at the reduction temperature of 850 °C for PBSF system. Among PBSF with complete phase reconstruction, the highly-populated Fe metal particles socketed on R-PBSF30 attributed to excellent electrochemical performances under both fuel cell (1.23 W cm−2 at 800 °C under H2 fuel) and electrolysis cell (−1.62 A cm−2 at 1.5 V and 800 °C under CO2 and H2O fuels) modes coupled with great durability. Our investigations strongly provide a pathway to explore new factors for the phase reconstruction and offer a new opportunity to discover prospective candidates with customized functionalities for next-generation energy-related applications.
Methods
Material synthesis
Pr0.5Ba0.5−xSrxFeO3−δ samples (x = 0, 0.1, 0.2, 0.3, 0.4, and 0.5, abbreviated as PBSF in Supplementary Table 1) and Pr0.5Sr0.5MnO3−δ were synthesized by the Pechini method. For PBSF materials, stoichiometric amounts of Pr(NO3)3·6H2O (Aldrich, 99.9%, metal basis), Ba(NO3)2 (Aldrich, 99 + %), Sr(NO3)2 (Aldrich, 99+%) and Fe(NO3)3·9H2O (Aldrich, 98+%) nitrate salts were dissolved in distilled water with the addition of quantitative amounts of citric acid and poly-ethylene glycol, while for Pr0.5Sr0.5MnO3−δ material, stoichiometric amounts of Pr(NO3)3·6H2O (Aldrich, 99.9%, metal basis), Sr(NO3)2 (Aldrich, 99+%) and Mn(NO3)2·4H2O (Aldrich, 97+%) nitrate salts were dissolved in distilled water with the addition of quantitative amounts of citric acid and poly-ethylene glycol. After removal of excess resin by heating at 280 °C, transparent organic resins containing metals in a solid solution were formed. The resins were calcined at 600 °C for 4 h and then sintered at 1200 °C for 4 h in air environment. The chemical compositions of the synthesized powders and their abbreviations are given in Supplementary Table 1.
Structural characterization
The crystal structures of the Pr0.5Ba0.5−xSrxFeO3−δ samples (x = 0, 0.3, and 0.5) and Pr0.5Sr0.5MnO3−δ after heat-treated in two different environmental conditions (sintered at 1200 °C for 4 h in air environment and reduced at 850 °C for 4 h in humidified H2 environment (3% H2O)) were first identified by powder XRD patterns (Bruker diffractometer (LYNXEYE 1D detector), Cu Kα radiation, 40 kV, 40 mA) in the 2 theta range of 20° < 2θ < 60°. To calculate the exact Bravais lattice of the PBSF, the samples were first pressed into pellets at 2 MPa for 30 s and then sintered at 1200 °C for 4 h in air atmosphere. The XRD patterns of air-sintered PBSF series and (Pr0.5Ba0.2Sr0.3)2FeO4+δ – Fe metal (R-PBSF30) samples were further measured by high-power (HP) XRD. (Max 2500 V, Cu Kα radiation, 40 kV, 200 mA) at a scanning rate of 1° min−1 and a range of 15° < 2θ < 105°. After the HP XRD measurement, the powder patterns and lattice parameters were analyzed by the Rietveld refinement technique using the GSAS II program. The surface analysis of Pr0.5Ba0.2Sr0.3FeO3−δ (A-PBSF30) sintered at 1200 °C for 4 h in air atmosphere and (Pr0.5Ba0.2Sr0.3)2FeO4+δ – Fe metal (R-PBSF30) reduced at 850 °C for 4 h in humidified H2 environment (3% H2O) were conducted on XPS analyses on ESCALAB 250 XI from Thermo Fisher Scientific with a monochromated Al-Kα (ultraviolet He1, He2) X-ray source. The X-ray absorption fine structure (XAFS) spectra of Fe K-edge for A-PBSF30, R-PBSF30, and two references (Fe foil and Fe2O3 powder) were measured on ionization detectors under fluorescence mode at the Pohang Accelerator Laboratory (PAL, 6D extended XAFS (EXAFS)). The XAFS and Fourier-transformed (FT) EXAFS spectra analysis were performed using the Athena (Demeter) program.
In-situ phase reconstruction tendency evaluation
The in-situ phase reconstruction tendency of Pr0.5Ba0.5−xSrxFeO3−δ (x = 0, 0.1, 0.2, 0.25, 0.3, 0.4, and 0.5) samples were identified by in-situ XRD measurements under humidified H2 condition (3% H2O). The Pr0.5Ba0.25Sr0.25FeO3−δ (A-PBSF25) sample was additionally synthesized by the Pechini method to evaluate the phase reconstruction tendency under reducing atmosphere. The Pr0.5Ba0.5−xSrxFeO3−δ (x = 0, 0.1, 0.2, 0.25, 0.3, 0.4, and 0.5) samples were sintered at 1200 °C for 4 h in air atmosphere to form simple perovskite structure with fine crystallinity. The reduction temperatures were ranged from 700 to 870 °C and 2 h were delayed at each temperature interval (Bruker D8 advance).
Electron microscopy analysis
The microstructures of (1) Pr0.5Ba0.5−xSrxFeO3−δ samples (x = 0, 0.3, and 0.5) sintered at 1200 °C for 4 h in air atmosphere, (2) Pr0.5Ba0.5−xSrxFeO3−δ samples (x = 0, 0.3, and 0.5)reduced at 850 °C for 4 h in humidified H2 environment (3% H2O), and (3) all PBSF samples sintered at 950 °C for 4 h in air atmosphere were investigated by using an SEM (Nova Nano FE-SEM). TEM analyses were conducted with a JEOL JEM 2100 F with a probe forming (STEM) Cs (spherical aberration) corrector at 200 kV.
Electrical conductivity measurements
The electrical conductivities of PBSF with respect to temperature were measured under air and 5% H2 environments by the 4-probe method. The samples were pressed into pellets of cylindrical shape and then sintered at 1400 °C for 4 h in air environment to reach an apparent density of ~90%. The electrical conductivities were first measured in air atmosphere from 300 to 800 °C with intervals of 50 °C, and then measured in wet 5% H2 atmosphere (Ar balance, 3% H2O) from 300 to 800 °C with intervals of 50 °C. The current and voltage were recorded by a Biologic Potentiostat to calculate the resistance, resistivity, and conductivity of samples.
Computational methods
DFT calculations were performed to investigate the appropriate dopants for the phase reconstruction to n = 1 R-P perovskite along with the role of Sr2+ concentration on phase reconstruction tendency of PBSF using the Vienna ab initio Simulation Package51,52. For the exchange-correlation, the generalized gradient approximation (GGA) based Predew-Burke-Ernzerhof functional was used53. The electron-ion interactions were described using the projector augmented wave potential54,55. A plane wave was expanded up to cutoff energy of 400 eV. Electronic occupancies were calculated using Gaussian smearing with a smearing parameter of 0.05 eV. For the bulk optimization, all internal atoms were relaxed using a conjugate gradient algorithm until the forces of each atom were lowered below 0.03 eV/Å with an energy convergence of 10−5 eV. GGA + U approach was used to correct the self-interaction errors with Ueff = 4.0 eV for Fe 3d orbital, Ueff = 3.3 eV for Co 3d orbital, Ueff = 4.0 eV for Mn 3d orbital, Ueff = 7.0 eV for Ni 3d orbital, and Ueff = 6.0 eV for Pr 4f orbital18,56,57. For the Brillouin zones of the formation energy calculation of cubic perovskite (2 × 2 × 4 super cell) and n = 1 R-P perovskite (2 × 2 × 1 super cell), 3 × 3 × 1 and 3 × 3 × 2 Monkhorst-Pack k-point sampling were used, respectively58. For the oxygen vacancy formation energy calculations of BO2 layer between two AO layers, PrO-terminated (001) slab model (2 × 2 surface, 8 layers with 2 fixed bottom layers, vacuum layer of 16 Å) were used. For the co-segregation energy calculations, FeO2-terminated (001) slab model ( × 2 surface, 8 layers with 3 fixed bottom layers, vacuum layer of 16 Å) were used. For the Brillouin zones of the oxygen vacancy formation energy and the co-segregation energy calculations, 3 × 3 × 1 and 1 × 1 × 1 Monkhorst-Pack k-point sampling were used. The optimized lattice parameters of four materials, A-PBSF00 (Ba:Sr = 16:0), Pr0.5Ba0.1875Sr0.3125FeO3−δ (Ba:Sr = 6:10), Pr0.5Ba0.125Sr0.375FeO3−δ (Ba:Sr = 4:12), and A-PBSF50 (Ba:Sr = 0:16) were used for model structures in the computational studies. For the Ba2+/Sr2+ mixed models, the most stable configurations among the total 5 different Ba configurations were used.
The relative energies required for the phase reconstruction from simple perovskite to n = 1 R-P perovskite (Erecon) of six model structures with different Sr2+ concentration were calculated using the total energy difference between simple perovskite and n = 1 R-P perovskite by following equation:
| 3 |
Where ER-P perov and Esimple perov are the total energy of simple perovskite (2 × 2 × 4 super cell) and R-P perovskite (2 × 2 × 1 super cell), is total energy of body-centered cubic Fe metal unit cell, and is the total energy of gas phase oxygen molecule.
The oxygen vacancy formation energies (Evf-O) of Pr0.5Ba0.5TO3−δ, Pr0.5Sr0.5TO3−δ (T = Mn, Co, Fe, and Ni), and four model structures with different Sr2+ concentrations were calculated using the lattice oxygen on the BO2 layer since the phase reconstruction from simple perovskite (ABO3) to n = 1 R-P perovskite (A2BO4) requires the formation of both oxygen and B-site vacancies. For the Pr0.5Ba0.5TO3−δ and Pr0.5Sr0.5TO3−δ (T = Mn, Co, Fe, and Ni) models, the most stable structure configurations were utilized for the oxygen vacancy formation energy calculations. For the four computational models with different Sr2+ concentrations, the most stable vacancy sites were utilized for Ba2+/Sr2+ mixed models with Ba:Sr = 6:10 and Ba:Sr = 4:12. The Evf-O was calculated by following equation:
| 4 |
where and are the total energies of PrO-terminated (001) perovskite slab model with and without the oxygen vacancy, respectively.
The co-segregation energy (Eco-seg) is defined as the total energy difference of two surface models that have different vacancy site. The co-segregation energies of four computational models with different Sr2+ concentrations were calculated by following equation:
| 5 |
where and are total energies of FeO2-terminated (001) perovskite slab model that have oxygen vacancy on surface FeO2 and bulk FeO2 layer, respectively.
Furthermore, the Gibbs free energy for oxygen vacancy formation of eight samples were calculated to include the temperature and oxygen partial pressure factors in the Evf-O calculations. The equations used for the Gvf-O calculations from the surface AO and BO2 layers in Pr0.5(Ba/Sr)0.5TO3−δ (T = Mn, Fe, Co, and Ni) are as follows:
| 6 |
| 7 |
| 8 |
| 9 |
| 10 |
The and are the total energies of PrO-terminated (001) perovskite slab model with and without the oxygen vacancy, respectively. The , , and are the Gibbs free energy of di-atomic oxygen molecule, hydrogen, and water molecule, respectively. The and is the gas phase energy of ground state triplet O2 molecule and hydrogen molecule, respectively. The zero point energies of oxygen molecule () and hydrogen molecule () were extracted from the previous calculated value59. The standard entropy of gas phase oxygen () was obtained from National Institute of Standards and Technology Chemistry Web-Book (http://webbook.nist.gov/chemistry). Moreover, the correction energy of oxygen molecule () was added to reconcile the Evf-O differences between the results achieved via computational method (GGA functional) and real experimental results60. The temperature and p(O2) are 750oC and 10−9 atm for Gvf-O calculations at the surface AO layer (Eq. 6 and 7) and the temperature, p(O2), p(H2), and p(H2O) values are 750oC, 10−9, 0.1, and 0.01 atm, respectively, for Gvf-O calculations at the BO2 layer (Eq. 8, 9, and 10). Under this specified condition (reducing condition), we assumed that the reduction of BO2 layer occurred via two elementary steps: surface hydrogen oxidation reaction () and oxygen vacancy diffusion toward the BO2 layer. The activation energy of oxygen vacancy diffusion (: 0.95 eV) was calculated from the electrochemical measurements (Arrhenius plot of area specific resistance) of Pr0.4Sr0.6Fe0.875Mo0.125O3−δ (PSFM) material under H2 condition61.
Electrochemical performance measurements
La0.9Sr0.1Ga0.8Mg0.2O3−δ (LSGM) powder was prepared by conventional solid-state reaction to fabricate LSGM electrolyte-supported symmetrical S-SOCs. Stoichiometric amounts of La2O3 (Sigma, 99.99%), SrCO3 (Sigma, 99.99%), Ga2O3 (Sigma, 99.99%) and MgO (Sigma, 99.9%) powders were first mixed in a mortar and then ball-milled in ethanol for 24 h to obtain the desired composition. After drying, the obtained powder was calcined at 1000 °C for 6 h. After formation of LSGM powder with desired stoichiometry, the electrolyte substrate was prepared by pressing at 2 MPa for 30 s into cylindrical shape and then sintered at 1475 °C for 5 h. The thickness of LSGM electrolyte was polished to about 250 μm. A La0.6Ce0.4O2-δ (LDC) as a buffer layer was also prepared by ball-milling stoichiometric amounts of La2O3 (Sigma, 99.99%) and CeO2 (Sigma, 99.99%) in ethanol for 24 h and then calcined at 1000 °C for 6 h. Electrode slurries were prepared by mixing pre-calcined powders of PBSF with an organic binder (Heraeus V006) and acetone in 3:6:0.6 weight ratio. The electrode inks were applied onto the LSGM pellet by a screen-printing method and then sintered at 950 °C for 4 h in air to achieve the desired porosity. The porous electrodes had an active area of 0.36 cm2 and a thickness of about 15 μm. The LDC layer was screen-printed between the electrode and electrolyte to prevent inter-diffusion of ionic species between electrode and electrolyte. The cells with configuration of Electrode |LDC | LSGM | LDC | Electrode were mounted on alumina tubes with ceramic adhesives (Ceramabond 552, Aremco) for electrochemical performance tests (Cross-sectional SEM image of the A-PBSF30 symmetrical cell given in Supplementary Fig. 20). Silver paste and silver wire were utilized for electrical connections to both the fuel electrode and air electrode. The entire cell was placed inside a furnace and heated to the desired temperature. I–V polarization curves of synthesized fuel cells with PBSF as both sides of electrodes were measured using a BioLogic Potentiostat in a temperature range of 700 to 800 °C (temperature interval: 50 °C) in humidified hydrogen (3% H2O) at a flow rate of 100 ml min−1. Fuel cell evaluation under humidified C3H8 fuel (3% H2O) at a flow rate of 100 ml min−1 were also performed for symmetrical solid oxide fuel cell (S-SOFC) test with cell composition A-PBSF30 | LDC | LSGM | LDC | A-PBSF30 from 700 to 800 °C (temperature interval: 50 °C) using a BioLogic Potentiostat. For the electrochemical performance test of S-SOC with the cell composition of A-PBSF30 | LDC | LSGM | LDC | A-PBSF30 during co-electrolysis, 50 ml min−1 of H2 and CO2 into a H2O-containing bubbler (with a heating tape) were co-fed to fuel electrode and 100 ml min−1 of air was fed to air electrode. The in-operando quantitative analysis of the generated synthetic gas (H2 and CO) during co-electrolysis of CO2 and H2O (Ratio of CO2:H2:H2O = 45:45:10) for the A-PBSF30 symmetrical cell (@800 °C and 1.5 V) was demonstrated by the gas chromatograph (Agilent 7820 A GC instrument) with a thermal conductivity detector and a packed column (Agilent carboxen 1000).
Supplementary information
Acknowledgements
This work was supported by the Korea Institute of Energy Technology Evaluation and Planning (KETEP) and the Ministry of Trade, Industry & Energy (MOTIE) of the Republic of Korea (No. 20213030030150) and the National Research Foundation (NRF) funded by the Ministry of Education (NRF-2019R1C1C1005801, NRF-2021M3I3A1084292, and NRF-2021R1A2C3004019). This work was also supported by “CO2 utilization battery for hydrogen production based on fault-tolerance deep learning” (No. 1.200097.01). The Xray absorption fine structure experiments performed at the beamline 6D of Pohang Accelerator Laboratory was supported by the Pohang University of Science and Technology (POSTECH) and Ulsan National Institute of Science and Technology Central Research Facilities center (UCRF).
Author contributions
H.K. and O.K. carried out most of the experimental works and contributed to manuscript writing. C.L. performed DFT calculations. M.T.C. gave help on additional DFT calculations. J.O. performed the gas chromatography (GC) analysis. H.Y.J. conducted TEM measurements and analyzed the TEM images. S.C., J.W.H., and G.K. designed the experiments and analyzed the data. All authors contributed to the discussions and analysis of the results regarding the manuscript.
Data availability
The data measured, simulated, and analyzed in this study are available from the corresponding author on reasonable request.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
These authors contributed equally: Hyunmin Kim, Chaesung Lim and Ohhun Kwon.
Change history
1/17/2022
The original version of the Peer Review File associated with this Article was updated shortly after publication.
Contributor Information
Sihyuk Choi, Email: sh.choi@kumoh.ac.kr.
Jeong Woo Han, Email: jwhan@postech.ac.kr.
Guntae Kim, Email: gtkim@unist.ac.kr.
Supplementary information
The online version contains supplementary material available at 10.1038/s41467-021-26739-1.
References
- 1.Sengodan S, et al. Layered oxygen-deficient double perovskite as an efficient and stable anode for direct hydrocarbon solid oxide fuel cells. Nat. Mater. 2015;14:205–209. doi: 10.1038/nmat4166. [DOI] [PubMed] [Google Scholar]
- 2.Neagu D, Tsekouoras G, Miller DN, Menard H, Irvine JTS. In situ growth of nanoparticles through control of non-stoichiometry. Nat. Chem. 2013;5:916–923. doi: 10.1038/nchem.1773. [DOI] [PubMed] [Google Scholar]
- 3.Kang KN, et al. Co3O4 exsolved defective layered perovskite oxide for energy storage systems. ACS Energy Lett. 2020;5:3828–3836. [Google Scholar]
- 4.Joo S, et al. Cation-swapped homogeneous nanoparticles in perovskite oxides for high power density. Nat. Commun. 2019;10:1–9. doi: 10.1038/s41467-019-08624-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Opitz AK, et al. Understanding electrochemical switchability of perovskite-type exsolution catalysts. Nat. Commun. 2020;11:1–10. doi: 10.1038/s41467-020-18563-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Irvine JTS, et al. Evolution of the electrochemical interface in high-temperature fuel cells and electrolysers. Nat. Energy. 2016;1:1–13. [Google Scholar]
- 7.Ding D, Li X, Lai SY, Gerdes K, Liu M. Enhancing SOFC cathode performance by surface modification through infiltration. Energy Environ. Sci. 2014;7:552–575. [Google Scholar]
- 8.Schlupp MVF, Evans A, Martynczuk J, Prestat M. Micro-solid oxide fuel cell membranes prepared by aerosol-assisted chemical vapor deposition. Adv. Energy Mater. 2014;4:1–7. [Google Scholar]
- 9.Kwak NW, et al. In situ synthesis of supported metal nanocatalysts through heterogeneous doping. Nat. Commun. 2018;9:1–8. doi: 10.1038/s41467-018-07050-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Jun A, Kim J, Shin J, Kim G. Achieving high efficiency and eliminating degradation in solid oxide electrochemical cells using high oxygen-capacity perovskite. Angew. Chem. Int. Ed. 2016;55:12512–12515. doi: 10.1002/anie.201606972. [DOI] [PubMed] [Google Scholar]
- 11.Choi S, et al. A robust symmetrical electrode with layered perovskite structure for direct hydrocarbon solid oxide fuel cells: PrBa0.8Ca0.2Mn2O5+δ. J. Mater. Chem. A. 2016;4:1747–1753. [Google Scholar]
- 12.Myung JH, Neagu D, Miller DN, Irvine JTS. Switching on electrocatalytic activity in solid oxide cells. Nature. 2016;537:528–531. doi: 10.1038/nature19090. [DOI] [PubMed] [Google Scholar]
- 13.Neagu D, et al. In situ observation of nanoparticle exsolution from perovskite oxides: from atomic mechanistic insight to nanostructure tailoring. ACS Nano. 2019;13:12996–13005. doi: 10.1021/acsnano.9b05652. [DOI] [PubMed] [Google Scholar]
- 14.Sun Y, et al. New opportunity for in situ exsolution of metallic nanoparticles on perovskite parent. Nano Lett. 2016;16:5303–5309. doi: 10.1021/acs.nanolett.6b02757. [DOI] [PubMed] [Google Scholar]
- 15.Kwon O, et al. Self-assembled alloy nanoparticles in a layered double perovskite as a fuel oxidation catalyst for solid oxide fuel cells. J. Mater. Chem. A. 2018;6:15947–15953. [Google Scholar]
- 16.Joo S, et al. Highly active dry methane reforming catalysts with boosted in situ grown Ni-Fe nanoparticles on perovskite via atomic layer deposition. Sci. Adv. 2020;6:1–9. doi: 10.1126/sciadv.abb1573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Zhang J, Gao MR, Luo JL. In situ exsolved metal nanoparticles: a smart approach for optimization of catalysts. Chem. Mater. 2020;32:5424–5441. [Google Scholar]
- 18.Kwon O, et al. Exsolution trends and co-segregation aspects of self-grown catalyst nanoparticles in perovskites. Nat. Commun. 2017;8:1–7. doi: 10.1038/ncomms15967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Liu S, Liu Q, Luo JL. Highly stable and efficient catalyst with in situ exsolved Fe-Ni alloy nanospheres socketed on an oxygen deficient perovskite for direct CO2 electrolysis. ACS Catal. 2016;6:6219–6228. [Google Scholar]
- 20.Sun Y, et al. A-site deficient perovskite: the parent for in situ exsolution of highly active, regenerable nano-particles as SOFC anodes. J. Mater. Chem. A. 2015;3:11048–11056. [Google Scholar]
- 21.Tsekouras G, Neagu D, Irvine JTS. Step-change in high temperature steam electrolysis performance of perovskite oxide cathodes with exsolution of B-site dopants. Energy Environ. Sci. 2013;6:256–266. [Google Scholar]
- 22.Zhu T, Troiani HE, Mogni LV, Han M, Barnett SA. Ni-substituted Sr(Ti,Fe)O3 SOFC anodes: achieving high performance via metal alloy nanoparticle exsolution. Joule. 2018;2:478–496. [Google Scholar]
- 23.Gao Y, Chen D, Saccoccio M, Lu Z, Ciucci F. From material design to mechanism study: nanoscale Ni exsolution on a highly active A-site deficient anode material for solid oxide fuel cells. Nano Energy. 2016;27:499–508. [Google Scholar]
- 24.Kim KJ, et al. Facet-dependent in situ growth of nanoparticles in epitaxial thin films: the role of interfacial energy. J. Am. Chem. Soc. 2019;141:7509–7517. doi: 10.1021/jacs.9b02283. [DOI] [PubMed] [Google Scholar]
- 25.Neagu D, et al. Demonstration of chemistry at a point through restructuring and catalytic activation at anchored nanoparticles. Nat. Commun. 2017;8:1–8. doi: 10.1038/s41467-017-01880-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Yang C, et al. In situ fabrication of CoFe alloy nanoparticles structured (Pr0.4Sr0.6)3(Fe0.85Nb0.15)2O7 ceramic anode for direct hydrocarbon solid oxide fuel cells. Nano Energy. 2015;11:704–710. [Google Scholar]
- 27.Lv, H. et al. In situ investigation of reversible exsolution/dissolution of CoFe alloy nanoparticles in a Co-doped Sr2Fe1.5Mo0.5O6-δ cathode for CO2 electrolysis. Adv. Mater. 32, 1906193 (2020). [DOI] [PubMed]
- 28.Yang C, et al. Sulfur-tolerant redox-reversible anode material for direct hydrocarbon solid oxide fuel cells. Adv. Mater. 2012;24:1439–1443. doi: 10.1002/adma.201104852. [DOI] [PubMed] [Google Scholar]
- 29.Du Z, et al. High-performance anode material Sr2FeMo0.65Ni0.35O6-δ with in situ exsolved nanoparticle catalyst. ACS Nano. 2016;10:8660–8669. doi: 10.1021/acsnano.6b03979. [DOI] [PubMed] [Google Scholar]
- 30.Chung YS, et al. In situ preparation of a La1.2Sr0.8Mn0.4Fe0.6O4 Ruddlesden-Popper phase with exsolved Fe nanoparticles as an anode for SOFCs. J. Mater. Chem. A. 2017;5:6437–6446. [Google Scholar]
- 31.Park S, et al. In situ exsolved Co nanoparticles on Ruddlesden-Popper material as highly active catalyst for CO2 electrolysis to CO. Appl. Catal. B Environ. 2019;248:147–156. [Google Scholar]
- 32.Kim K, et al. Mechanistic insights into the phase transition and metal ex-solution phenomena of Pr0.5Ba0.5Mn0.85Co0.15O3−δ from simple to layered perovskite under reducing conditions and enhanced catalytic activity. Energy Environ. Sci. 2021;14:873–882. [Google Scholar]
- 33.Vibhu V, et al. Characterization of PrNiO3-δ as oxygen electrode for SOFCs. Solid State Sci. 2018;81:26–31. [Google Scholar]
- 34.Choi S, et al. Highly efficient and robust cathode materials for low-temperature solid oxide fuel cells: PrBa0.5Sr0.5Co2−xFexO5+δ. Sci. Rep. 2013;3:1–6. doi: 10.1038/srep02426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Chen C, Ciucci F. Designing Fe-based oxygen catalysts by density functional theory calculations. Chem. Mater. 2016;28:7058–7065. [Google Scholar]
- 36.Brown JJ, Ke Z, Geng W, Page AJ. Oxygen vacancy defect migration in titanate perovskite surfaces: effect of the A-site cations. J. Phys. Chem. C. 2018;122:14590–14597. [Google Scholar]
- 37.Kwon O, et al. Probing one-dimensional oxygen vacancy channels driven by cation-anion double ordering in perovskites. Nano Lett. 2020;20:8353–8359. doi: 10.1021/acs.nanolett.0c03516. [DOI] [PubMed] [Google Scholar]
- 38.Neagu D, et al. Nano-socketed nickel particles with enhanced coking resistance grown in situ by redox exsolution. Nat. Commun. 2015;6:1–8. doi: 10.1038/ncomms9120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Niu B, et al. In-situ growth of nanoparticles-decorated double perovskite electrode materials for symmetrical solid oxide cells. Appl. Catal. B Environ. 2020;270:118842. [Google Scholar]
- 40.Kim H, Joo S, Kwon O, Choi S, Kim G. Cobalt-free Pr0.5Ba0.4Sr0.1FeO3-δ as a highly efficient cathode for commercial YSZ-supported solid oxide fuel cell. ChemElectroChem. 2020;7:4378–4382. [Google Scholar]
- 41.Liu BQ, Dong X, Xiao G, Zhao F, Chen F. A novel electrode material for symmetrical SOFCs. Adv. Mater. 2010;22:5478–5482. doi: 10.1002/adma.201001044. [DOI] [PubMed] [Google Scholar]
- 42.Lu X, et al. Mo-doped Pr0.6Sr0.4Fe0.8Ni0.2O3-δ as potential electrodes for intermediate-temperature symmetrical solid oxide fuel cells. Electrochim. Acta. 2017;227:33–40. [Google Scholar]
- 43.He W, Wu X, Dong F, Ni M. A novel layered perovskite electrode for symmetrical solid oxide fuel cells: PrBa(Fe0.8Sc0.2)2O5+δ. J. Power Sources. 2017;363:16–19. [Google Scholar]
- 44.Zhang Y, Zhao H, Du Z, Świerczek K, Li Y. High-performance SmBaMn2O5+δ electrode for symmetrical solid oxide fuel cell. Chem. Mater. 2019;31:3784–3793. [Google Scholar]
- 45.Cai H, et al. Cobalt–free La0.5Sr0.5Fe0.9Mo0.1O3–δ electrode for symmetrical SOFC running on H2 and CO fuels. Electrochim. Acta. 2019;320:134642. [Google Scholar]
- 46.Lu C, et al. Efficient and stable symmetrical electrode La0.6Sr0.4Co0.2Fe0.7Mo0.1O3–δ for direct hydrocarbon solid oxide fuel cells. Electrochim. Acta. 2019;323:134857. [Google Scholar]
- 47.Hansen JB. Solid oxide electrolysis - a key enabling technology for sustainable energy scenarios. Faraday Discuss. 2015;182:9–48. doi: 10.1039/c5fd90071a. [DOI] [PubMed] [Google Scholar]
- 48.Zhu J, et al. Enhancing CO2 catalytic activation and direct electroreduction on in-situ exsolved Fe/MnOx nanoparticles from (Pr,Ba)2Mn2-yFeyO5+δ layered perovskites for SOEC cathodes. Appl. Catal. B Environ. 2020;268:118389. [Google Scholar]
- 49.Zhou Y, et al. Enhancing CO2 electrolysis performance with vanadium-doped perovskite cathode in solid oxide electrolysis cell. Nano Energy. 2018;50:43–51. [Google Scholar]
- 50.Kim C, et al. Highly efficient CO2 utilization via aqueous zinc–or aluminum–CO2 systems for hydrogen gas evolution and electricity production. Angew. Chem. Int. Ed. 2019;58:9506–9511. doi: 10.1002/anie.201904763. [DOI] [PubMed] [Google Scholar]
- 51.Kresse G, Hafner J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B. 1993;47:558–561. doi: 10.1103/physrevb.47.558. [DOI] [PubMed] [Google Scholar]
- 52.Sholl. D. & Steckel, J. A. Density functional theory: a practical introduction. (John Wiley & Sons, Inc., 2011)
- 53.Perdew JP, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996;77:3865–3868. doi: 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- 54.Blöchl PE. Projector augmented-wave method. Phys. Rev. B. 1994;50:17953–17979. doi: 10.1103/physrevb.50.17953. [DOI] [PubMed] [Google Scholar]
- 55.Kresse G, Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B. 1999;59:1758–1775. [Google Scholar]
- 56.Kirklin S, et al. The open quantum materials database (OQMD): assessing the accuracy of DFT formation energies. npj Comput. Mater. 2015;1:1–15. [Google Scholar]
- 57.Bouadjemi B, Bentata S, Abbad A, Benstaali W, Bouhafs B. Half-metallic ferromagnetism in PrMnO3 perovskite from first principles calculations. Solid State Commun. 2013;168:6–10. [Google Scholar]
- 58.Monkhorst HJ, Pack JD. Special points for Brillouin-zone integrations. Phys. Rev. B. 1976;13:5188. [Google Scholar]
- 59.Nørskov JK, et al. Origin of the overpotential for oxygen reduction at a fuel-cell cathode. J. Phys. Chem. B. 2004;108:17886–17892. [Google Scholar]
- 60.Wang L, Maxisch T, Ceder G. Oxidation energies of transition metal oxides within the GGA + U framework. Phys. Rev. B. 2006;73:195107. [Google Scholar]
- 61.Zhang D, et al. Preparation and characterization of a redox-stable Pr0.4Sr0.6Fe0.875Mo0.125O3-δ material as a novel symmetrical electrode for solid oxide cell application. Int. J. Hydrog. Energy. 2020;45:21825–21835. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data measured, simulated, and analyzed in this study are available from the corresponding author on reasonable request.