Figure 1.
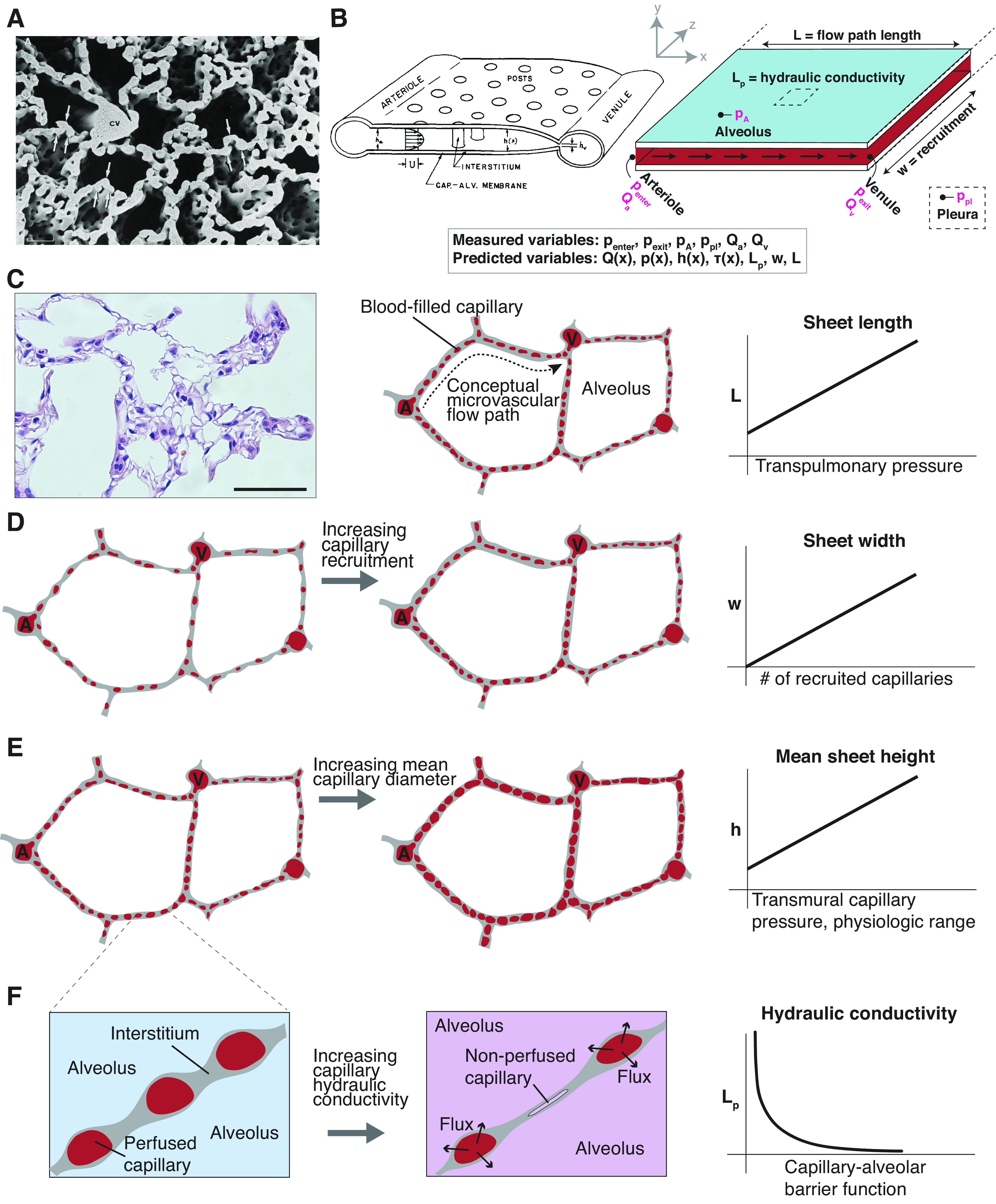
Permeable sheet-flow setup and schema of vascular cast of the alveolar capillary network in adult rat lung (A), reproduced with permission from Caduff et al. (22). The dense, intersecting nature of the pulmonary microvascular makes it appropriately modeled as a continuous “sheet” of blood flowing from many arteriolar sources to many venular sinks. B: schema of pulmonary sheet flow, from Fung 1974, and adaptation showing measurable and solvable variables, including the capillary pressure p(x), diameter/capillary sheet height h(x), flow Q(x), shear stress τ(x), length (L), sheet width (w), and barrier hydraulic conductivity (Lp). Directly measurable parameters , , pA, ppl, Qa, and Qv are emphasized in magenta. C: rat pulmonary histology (H&E) and schematic articulating arteriole (A) to venule (V) flow path. Scale bar = 50 µm. The mean distance between arteriolar sources and venular sinks changes slightly with increasing transpulmonary pressure. D: capillaries with intramural flow are recruited while those with no flow are not. Increasing capillary recruitment is reflected by an increase in the output parameter w. E: capillaries are highly elastic and can distend in diameter in response to increased arteriolar and/or venular pressure. The height h(x) of the pulmonary blood sheet is the mathematical representation of capillary diameter along flow path length L. F: increased barrier hydraulic conductivity causes an increase in transmural flux which must be accounted for in fluidic model. We hypothesized that an increase in Lp would cause a decrease in steady-state capillary diameters and might affect parenchymal recruitment. Lp is a permeability metric and, all else being equal, is inversely related to total organ barrier resistance.
