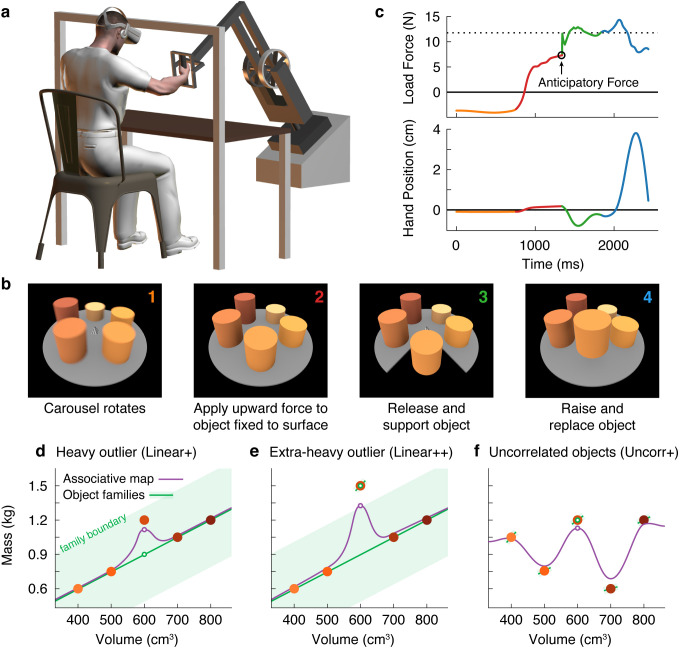
Figure 1. Object families and associative maps make different predictions for an outlier lifting task.

(a) Participants grasped the handle of a three-dimensional robotic interface (3BOT) with their right hand and viewed stereoscopic scenes (Oculus Rift). The 3BOT could track movement and simulate the haptic experience of manipulating objects. (b) Screenshots of the key stages of the lifting task. See text for details. (c) Load force and vertical position traces from an example trial, color-coded to match the numbers in (b). In this example, the anticipatory force was less than the weight of the object (dotted line), causing a downward movement of the hand and object. (d-f) Tasks used to examine family representations. In these tasks there were five visually similar objects of varying volume and mass. In the Linear+ condition (d), four of the objects had a linear relation between size and weight. A fifth object of intermediate size had a higher density (hence the + notation) and therefore was an outlier. Under the object families hypothesis, the four objects induce learning of the family structure (green line). Visually similar objects that fall within the category boundary for the family (shaded green region) are treated as family members. Because the outlier falls within the category boundary, its weight should be persistently misestimated based on the family structure (green circle). Under the associative map hypothesis, exposure to the outlier leads to partial learning of its actual weight (purple circle). In the Linear++ condition (e), the object families hypothesis predicts that when the outlier becomes sufficiently extreme, and crosses the family boundary, it will be categorized as an individual and its weight fully learned. The associative map hypothesis still predicts partial learning of this outlier. In the Uncorr+ condition (f), when size and weight are uncorrelated, the object families hypothesis predicts that the object weights will each be learned individually. Under the associative map hypothesis, there is no fundamental difference between this scenario and those depicted in (d, e), so the predictions for learning are similar to the object families hypothesis (i.e. all five objects will eventually be learned).