Ion sensing with single charge resolution using sub–10-nm electrical double layer–gated silicon nanowire transistors

Activities of a single hydrogen ion are directly detected using sub–10-nm silicon nanowire transistors.

Abstract

Electrical sensors have been widely explored for the analysis of chemical/biological species. Ion detection with single charge resolution is the ultimate sensitivity goal of such sensors, which is yet to be experimentally demonstrated. Here, the events of capturing and emitting a single hydrogen ion (H⁺) at the solid/liquid interface are directly detected using sub–10-nm electrical double layer–gated silicon nanowire field-effect transistors (SiNWFETs). The SiNWFETs are fabricated using a complementary metal-oxide-semiconductor compatible process, with a surface reassembling step to minimize the device noise. An individually activated surface Si dangling bond (DB) acts as the single H⁺ receptor. Discrete current signals, generated by the single H⁺-DB interactions via local Coulomb scattering, are directly detected by the SiNWFETs. The single H⁺-DB interaction kinetics is systematically investigated. Our SiNWFETs demonstrate unprecedented capability for electrical sensing applications, especially for investigating the physics of solid/liquid interfacial interactions at the single charge level.

INTRODUCTION

Electrical sensors for chemical/biological substances have attracted great interest owing to their capability of label-free, real-time, and rapid analysis, as well as the possibility of miniaturization (1). Ion detection with single charge resolution is a highly sought-after goal for the electrical sensors. It can provide a powerful technology to resolve individual quanta of analyte and to investigate the physics of solid/liquid interfacial interactions at the single charge level. The nanoscale field-effect transistor (FET) is a promising candidate for such goal because of its superior charge sensitivity (2–6). Electrical detections of a single DNA (7, 8) or protein (9) molecule in liquid samples have been reported using FET sensors based on the bottom-up fabricated self-assembled nanostructures, such as nanowires (9) or carbon nanotubes (7, 8). However, direct detection of a single charge in the liquid has not been reached in the reports. In addition, the complexity of the device fabrication based on self-assembled nanostructures greatly limits the large-scale integration and applications (10, 11).

In contrast to the bottom-up approach, top-down fabricated silicon nanowire (SiNW) FETs are fully compatible with the standard complementary metal-oxide-semiconductor (CMOS) fabrication technology. These SiNWFET sensors have been used for detection of ions (12–14) and molecules (15, 16) with ultrahigh sensitivity. The potential for single charge detection using such SiNWFET sensors was also theoretically predicted many years ago (17). However, because of the limitation in signal-to-noise ratio (SNR), electrical ion detection at the single charge level remains to be experimentally demonstrated. A SiNWFET sensor is normally gated via an oxide-based gate dielectric layer, which inevitably separates the impinging target charge from the channel and thus suppresses the signal generation. On the other hand, the top-down process induced roughness and defects on the SiNW surface contribute considerably to the intrinsic device noise (18). In addition to the challenges of SNR, to time-resolve a single target-receptor interaction event on a sensor surface, it is also very critical to limit the total number of receptors to a few.

Here, we designed and fabricated sub–10-nm SiNWFETs with the standard top-down Si fabrication method. A H₂ annealing process was used to reassemble an atomically smooth SiNW surface and thus minimize the defect-induced intrinsic device noise. Our SiNWFET sensors were made with a gate oxide–free configuration, in which the electrical double layer (EDL) in the liquid acted as the gate insulator. This configuration, with a clean silicon sensing surface and no intervening oxide, enabled the target charge binding directly on the channel surface and therefore improved the detection sensitivity. In addition, most of the Si dangling bonds (DBs) on the SiNW surface were passivated by covalent H-terminations during the native oxide etching step in buffered hydrogen fluoride (BHF). The few remaining DBs could be individually activated as single hydrogen ion (H⁺) receptors via gate voltage modulation. The single H⁺-DB interactions were directly detected by our EDL-gated SiNWFETs, represented as discrete drain-to-source current (I_DS) switching between two levels. The kinetics of the interactions and its correlation with the energy barrier at the solid/liquid interface were systematically investigated. The signal transduction mechanism was also identified. Our EDL-gated SiNWFET sensors demonstrate the unprecedented capability to investigate the physics of solid/liquid interface at the single charge level and hold great potential for future biochemical sensing applications.

RESULTS

Process optimization for sub–10-nm SiNWFETs

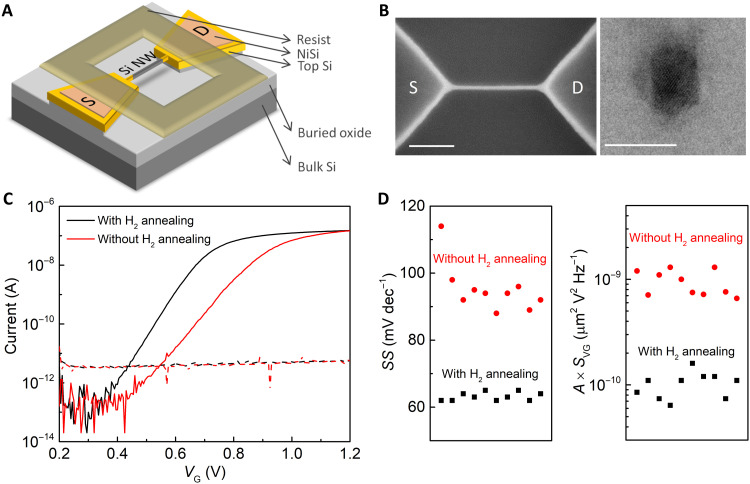
A three-dimensional schematic of the sub–10-nm gate oxide–free SiNWFET is shown in Fig. 1A. The SiNWFET was fabricated on a (100) silicon-on-insulator (SOI) wafer with the standard Si process technology. The source (S) and drain (D) regions of the SiNWFET are heavily n-doped (yellow), while the SiNW channel consists of a 150-nm-long lightly doped p-type region (gray). Detailed description of the fabrication process can be found in Materials and Methods and figs. S1 and S2.

Fig. 1. SiNWFET fabrication process optimization.

(A) Three-dimensional schematic of a SiNWFET. The SiNW consists of a lightly p-doped region (gray) in the center and a heavily n-type region (yellow) on each side. (B) SEM image (left; scale bar, 100 nm) and cross-sectional TEM image (right; scale bar, 10 nm) of a SiNWFET with H₂ annealing. (C) Typical transfer characteristics of SiNWFETs with and without H₂ annealing measured in 1 mM KCl at V_DS = 10 mV. The solid and dashed lines mean I_DS and gate leakage current, respectively. (D) Summary of SS (left) and A × S_VG at 10 Hz (right) of 10 SiNWFETs with and without H₂ annealing measured in 1 mM KCl at V_DS = 10 mV.

To detect the single H⁺ capture/emission events, the intrinsic device noise of SiNWFET must be lower than the single charge signal. The intrinsic noise of SiNWFET strongly depends on the defect density on SiNW surface and is inversely proportional to gate area (section S3) (18–20). For our sub–10-nm SiNW, the process-induced surface roughness becomes comparable with SiNW diameter as shown by the scanning electron microscope (SEM) image in fig. S3A. Such roughness and its associated surface defects could contribute notably to the device noise. The surface roughness problem was addressed by annealing the SiNW structure in a H₂ ambient. The annealing facilitates migration of surface Si atoms to the lower-energy sites and a reassembly of the surface at the temperature well below the Si melting point (21, 22). Such reassembly process removes the process-induced surface defects and leads to atomically smooth channel surface, as evidenced by the SEM image of the SiNWFET after H₂ annealing in Fig. 1B (left). In addition, the SiNW channel diameter is further reduced because of the migration of Si atoms on the SiNW surface to the large-size S/D pads to lower the total free energy (fig. S3B) (21). A cross-sectional transmission electron microscope (TEM) image of the smoothed SiNW channel is shown in Fig. 1B (right). The channel width and height measured from the image are 7 and 9 nm, respectively.

After fabrication, the SiNWFETs were measured in an electrolyte containing 1 mM KCl. A gate voltage (V_G) was applied via an Ag/AgCl reference electrode, with the EDL at the SiNW/electrolyte interface acting as the gate dielectric layer. Figure 1C depicts the I_DS versus V_G curves of the SiNWFETs with and without H₂ annealing. Extracted subthreshold slopes (SS) of 10 devices on the same chip are plotted in Fig. 1D (left). H₂ annealing indeed greatly improved the electrical performance of the SiNWFETs, as evidenced by their near-ideal SS ~60 mV dec⁻¹ and much-reduced spread in threshold voltage (V_T) among the devices (fig. S4). The gate-referred voltage noise S_VG at 10 Hz, after gate area (A) normalization, was lowered by about one order of magnitude by H₂ annealing, i.e., on average, from ~1 × 10⁻⁹ to ~1 × 10⁻¹⁰ μm² V² Hz⁻¹ (Fig. 1D, right). Note that A × S_VG achieved in this work is comparable to or even lower than some of the state-of-the-art SiNWFETs (15, 23). Output characteristics of the SiNWFETs and more noise data can be found in figs. S5 and S6, respectively.

The number of H⁺ receptors, i.e., surface Si DBs, on the SiNW channel is critical for single charge detection and therefore is carefully engineered in this work. The Si atom has four valence electrons and requires four bonds to saturate the valence shell. On the SiNW surface, nonsaturated valence electrons could form DBs, which can capture H⁺ from the electrolyte. The density of these DBs on (100) Si surface is approximately 10¹⁴ cm⁻² eV⁻¹. Considering the dimensions of our SiNW channel, the total number of DBs will be ~3000, which is too high for detecting single H⁺. It is known that oxygen atoms can terminate the Si DBs by forming an oxide layer and lower their density to ~10¹² cm⁻² eV⁻¹ (24). Upon BHF etching of the formed oxide, most of Si DBs will be passivated with covalent H-terminations, and the DB density will be further reduced to ~10¹⁰ cm⁻² eV⁻¹ (25, 26). In our process flow, the surface DB density of the SiNW was controlled by a native oxide etching step in BHF. After being passivated in BHF, the number of DBs is estimated to be 0.3 per SiNW, suggesting a high probability of a single H⁺ receptor activated on the tiny SiNW channel surface.

Detection of single H⁺

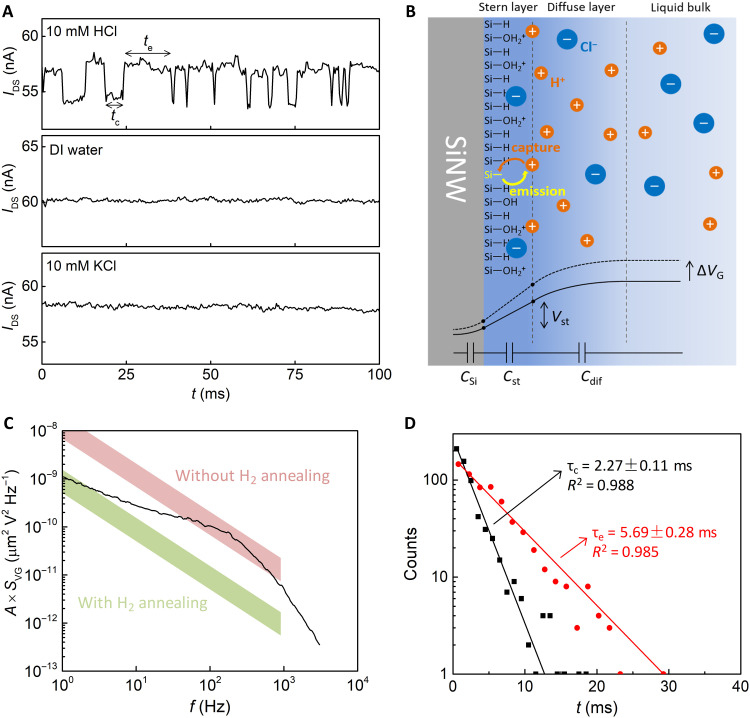
Detection of single H⁺ capture/emission events was conducted in a 10 mM HCl solution, with a constant gate overdrive, i.e., V_G − V_T = 129.4 mV. I_DS of the SiNWFET was monitored in real time, with a sampling frequency of 3 kHz. Figure 2A (top) depicts a typical I_DS time trace, which switches between two levels (ΔI_DS = 3 nA). For a nanoscale transistor with gate oxide, capture and emission of a carrier by a trap at Si/oxide interface could also result in the similar I_DS switching (27, 28). To verify whether the two-level I_DS switching correlates to the carrier trapping/detrapping in the solid-state FET channel, a control experiment was performed on the same SiNWFET but in deionized (DI) water. I_DS in the control experiment was intentionally kept the same as that in 10 mM HCl to ensure that the SiNW channel was biased to the same condition for both cases. As seen in Fig. 2A (middle), the I_DS trace measured in DI water does not switch between the two levels. This result excludes the possibility that the two-level I_DS switching is generated inside in the SiNWFET device. Another control experiment was conducted in a 10 mM KCl solution to examine the contribution of Cl⁻ to the I_DS switching. As shown in Fig. 2A (bottom), such I_DS switching is neither observed. This further confirms that the I_DS switching is generated by the interactions between H⁺ (not Cl⁻) and the DB. Please note that a H⁺ ion binds with a water molecule and forms a hydronium ion in the liquid sample. The terms of H⁺ are used for simplicity.

Fig. 2. Detection of single H⁺-DB interactions.

(A) I_DS traces recorded in 10 mM HCl, DI water, and 10 mM KCl. The sampling frequency is 3 kHz. (B) Schematic of SiNW/electrolyte interface. The single DB captures/emits H⁺ from/to the Stern/diffuse layer interface. The total potential drop across the interface is shared by the capacitances of SiNW (C_Si), Stern layer (C_st), and diffuse layer (C_dif). (C) A × S_VG (black curve) generated by single H⁺-DB interactions measured in 10 mM HCl, showing a Lorentzian shape with a corner frequency of ~150 Hz. The intrinsic device noise of the SiNWFET with H₂ annealing (green band) is much lower than the single charge signal, while that of the SiNWFET without H₂ annealing (red band) overwhelms the signal. (D) Statistical analysis of capture and emission times of single H⁺-DB interaction kinetics. They are in good agreement with Poisson distribution. The time constants τ_c and τ_e are extracted from the fitted slopes. R², coefficient of determination.

Our SiNWFET was biased to strong inversion with an electron conduction channel during the sensing experiments. The DB on the SiNW channel surface under strong inversion could be an electron acceptor (29) and saturated by an additional electron from the channel. Since the saturated DB is negatively charged, it could induce local Coulomb scattering in the SiNW channel. However, this negatively charged DB could further capture a H⁺ ion from the electrolyte and become neutralized. This would weaken the local Coulomb scattering and lead to an increase of I_DS. Therefore, the time when I_DS stays at the low state is regarded as the capture time t_c, as annotated in Fig. 2A (top). Correspondingly, the emission time t_e is the time that I_DS remains at the high state.

Figure 2B presents a schematic of the SiNW/electrolyte interface. The SiNW surface has three different terminations, i.e., single Si DB, covalent Si-H terminations, and Si-O⁻ terminations on discrete native oxide islands. The EDL formed on the electrolyte side consists of a Stern layer and a diffuse layer (30). The capacitances of the Stern layer (C_st) and diffuse layer (C_dif) are connected in series with the SiNW capacitance (C_Si). The electrical potential distribution across the SiNW/electrolyte interface is also illustrated in Fig. 2B. The single DB can capture/emit a H⁺ ion from/to the Stern/diffuse layer interface, which is the closest plane that H⁺ can reach toward the SiNW surface. In the emission process, from the DB to the electrolyte, the single H⁺ must overcome the electrical potential barrier across the Stern layer (V_st). The Si-O⁻ group on the surface can also interact with H⁺ ions and generate a weak pH response (fig. S7), which can be well described by the site-binding and the Gouy-Chapman-Stern (GCS) models (31, 32). Fitting of the pH response of our SiNWFET with the GCS model yields an effective –OH group density N_OH = 6 × 10¹³ cm⁻².

The time trace in Fig. 2A (top) is further analyzed in frequency domain, and its power spectrum density (PSD) is depicted in Fig. 2C, showing a Lorentzian shape profile with a corner frequency f_c ~150 Hz. In the same graph, the intrinsic device noise characteristics of SiNWFETs, with and without H₂ annealing, are also included as references. The Lorentzian hump is completely overshadowed by the intrinsic device noise of the SiNWFET without H₂ annealing, making the H⁺ capture/emission events undetectable. Distributions of t_c (black rectangles) and t_e (red circles) extracted from the I_DS trace are presented in Fig. 2D. The distributions are in excellent agreement with Poisson statistics (33). Time constants of capture (τ_c) and emission (τ_e), calculated as the mean values of t_c and t_e, i.e., τ_c = 〈t_c〉 and τ_e = 〈t_e〉, are 2.27 and 5.69 ms, respectively.

H⁺-DB interaction kinetics analysis

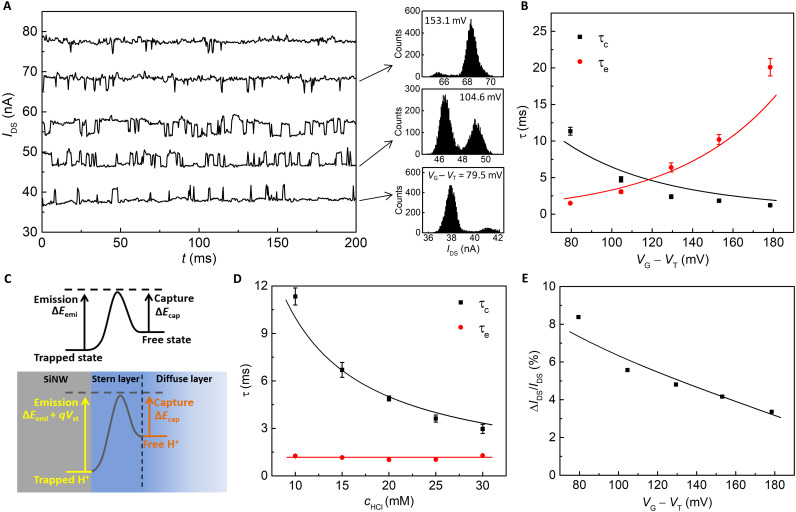
Figure 3A plots the I_DS traces of the SiNWFET (hereafter referred to as Dev. A), recorded at different V_G − V_T in 10 mM HCl. Three representative I_DS histograms are also included, showing two discrete Gaussian peaks of each trace. A more comprehensive set of I_DS histograms can be found in fig. S8. Again, the peak at lower I_DS represents the empty state of the DB, while the one at higher I_DS represents the filled state. At low V_G, i.e., V_G − V_T = 79.5 mV, the lower peak is dominating, indicating that the DB is mostly H⁺-empty. As V_G increases, the lower peak gradually diminishes, while the higher peak increases and finally becomes dominant, indicating that the DB is mostly filled with a H⁺ ion. The transition from empty to filled status with increasing V_G can be quantitatively represented by the increase of occupation probability P (fig. S9A), which is calculated by the ratio of the areas of the lower and higher Gaussian peaks. As V_G increases, Stern layer shares a larger potential drop. Therefore, the energy of a H⁺ ion at the DB is lowered compared to that at the Stern/diffuse layer interface (Fig. 2B). Consequently, the DB has a higher probability to be filled by the H⁺ from the Stern/diffuse layer interface at higher V_G. PSD of the time traces in Fig. 3A is also plotted in fig. S10, all showing a Lorentzian shape profile with f_c dependent on V_G − V_T.

Fig. 3. Analysis of single H⁺-DB interactions of Dev. A.

(A) I_DS traces recorded at various V_G − V_T in 10 mM HCl with 3-kHz sampling frequency. The histograms of I_DS present the change of occupancy status of the single DB by V_G. (B) Extracted τ_c and τ_e as a function of V_G − V_T. (C) Schematics of energy barriers of a general analyte-receptor reaction process (top) and the H⁺ capture and emission process on the SiNWFET surface (bottom). (D) τ_c and τ_e as a function of HCl concentration at I_DS = 40 nA. (E) Relative signal amplitude as a function of V_G − V_T. The solid curves in (B), (D), and (E) are the fitting results.

Figure 3B plots τ_c and τ_e extracted from the I_DS traces in Fig. 3A. τ_c decreases with increasing V_G, while τ_e shows an opposite trend. As V_G increases, the voltage drops across both diffuse layer and Stern layer are enlarged, as illustrated by the dashed line of the potential distribution in Fig. 2B. The increased potential drop in the diffuse layer will lead to an increased H⁺ concentration at the Stern/diffuse layer interface (c_Hs), which obeys the Boltzmann distribution in the diffuse layer (34). Consequently, it becomes easier for the DB to capture a H⁺ ion from the Stern/diffuse layer interface, leading to a shorter τ_c. At the same time, the emission of H⁺ from the DB becomes more difficult because of the enlarged potential barrier across the Stern layer. Therefore, τ_e increases with increasing V_G.

The time constants can be further correlated to reaction kinetics. In a reaction between analyte and its receptor on a surface, the association (k_on) and dissociation (k_off) constants depend on the kinetic energy barriers of the capture (ΔE_cap) and emission (ΔE_emi), respectively (see Fig. 3C, top). However, for the H⁺-DB interactions in our system, the potential drop across the Stern layer will add an additional barrier qV_st (q is the elemental charge) to the H⁺ emission process, as illustrated in Fig. 3C (bottom). Therefore, τ_c and τ_e of the H⁺-DB interactions can therefore be expressed as

$$\frac{1}{{\mathrm{\tau }}_{\mathrm{c}}}=k_{\text{on}}{c}_{\text{Hs}} \text{and}\frac{1}{{\mathrm{\tau }}_{\mathrm{e}}}=k_{\text{off}}{e}^{-\frac{{\mathit{qV}}_{\text{st}}}{\mathit{kT}}}$$ (1)

where k is the Boltzmann constant and T is the temperature. More details of Eq. 1 can be found in section S12. The potential and charge distribution at the SiNW/electrolyte interface (including c_Hs and V_st) can be calculated numerically using the site-binding and GCS models (see Materials and Methods) (31, 32, 34, 35). With these inputs, the measured time constant data at different V_G can be fitted by Eq. 1, shown as solid curves in Fig. 3B. Parameters C_st, k_on, and k_off of Dev. A extracted from the fitting are listed in table S1.

τ_c and τ_e were also measured at different bulk HCl concentrations (c_HCl), ranging from 10 to 30 mM with a fixed I_DS of 40 nA, as shown in Fig. 3D. τ_c decreases, while τ_e does not vary with increasing c_HCl. This is due to the negligible pH sensitivity in the c_HCl range between 10 and 30 mM (pH 2 to 1.5 in fig. S7), which indicates that the change of the electrical potential across the EDL is negligible in this pH range. c_Hs then follows the increase of c_HCl to maintain a constant potential drop across the diffuse layer. Higher c_Hs will lead to a reduced τ_c, as analytically expressed in Eq. 1. On the other hand, since V_st has negligible change in this pH range either, τ_e remains constant.

Figure 3E plots the relative amplitude (ΔI_DS/I_DS) at different V_G − V_T, where ΔI_DS is the difference of the two peak values in the I_DS histograms. Both carrier number (ΔN) and mobility (Δμ) fluctuations can contribute to the detected signals, i.e., ΔI_DS/I_DS = ΔN/N + Δμ/μ (36). The contribution from ΔN/N induced by single H⁺-DB interactions, as estimated in section S13, is negligible compared to the measured ΔI_DS/I_DS. Therefore, ΔI_DS/I_DS is mainly ascribed to Δμ/μ owing to the change of local Coulomb scattering strength induced by a single charge. ΔI_DS/I_DS decreases because of the reduced mobility and scattering coefficient at higher V_G (eq. S8). The measured ΔI_DS/I_DS can be well fitted by the mobility fluctuation shown as the solid curve in Fig. 3E (see section S14 for more details). The extracted scattering coefficient falls into the range of 5.4 × 10⁻¹⁵ to 8.4 × 10⁻¹⁵ V s (table S1), which is in good agreement with the reported value (~10⁻¹⁵ V s) (37).

One-by-one DB activation with increased V_G

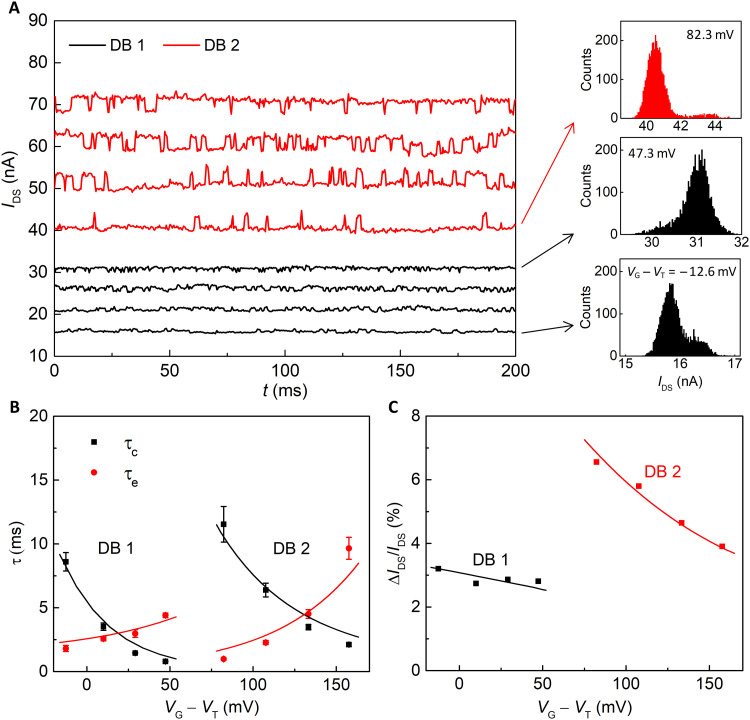
The measured single H⁺-DB interactions also discovered that multiple DBs on our SiNWFET surface could be activated individually. As shown in Fig. 4A, the I_DS traces measured on a different SiNWFET (Dev. B) can be separated into two groups depending on V_G. The first DB (DB 1) is activated at V_G − V_T = −12.6 mV, and its occupation status has a similar V_G dependence as Dev. A. DB 1 is mostly filled at V_G − V_T = 47.3 mV. As V_G − V_T further increases, i.e., above 82.3 mV, the second DB (DB 2) starts to interact with H⁺. Detailed histograms of the I_DS traces are presented in fig. S13, and their occupation probabilities are shown in fig. S9B. Figure 4B depicts τ_c and τ_e for the two DBs in Dev. B at different V_G, which can also be well fitted with the same C_st value in Dev. A (see the solid curves in Fig. 4B). The fitted parameters are listed in table S1. The equilibrium constant K = k_on/k_off of the two DB differs by ~20 times (table S1), indicating ~78 mV energy difference between DB 1 and DB 2 in the energy bandgap. This energy difference is consistent with the difference of V_G to activate DB 1 and DB 2. As shown in Fig. 4C, ΔI_DS/I_DS of both DBs can be well fitted with mobility fluctuation, and the extracted α_sc is listed in table S1. α_sc differs largely for the two DBs, which further confirms that they are distinct DBs. Although more than one DB might exist on the SiNW surface, they can be activated individually by V_G for single charge detection.

Fig. 4. One-by-one activation of DBs of Dev. B.

(A) I_DS traces recorded at different V_G − V_T in 10 mM HCl with 3-kHz sampling frequency. (B) τ_c and τ_e of the two DBs as a function of V_G − V_T. (C) Relative signal amplitude as a function of V_G − V_T. The solid curves in (B) and (C) are the fitting results.

DISCUSSION

Sub–10-nm EDL-gated SiNWFETs were fabricated using a CMOS-compatible process. The SiNW surface was smoothed with a H₂ annealing process to minimize the intrinsic device noise. The majority of the surface Si DBs were passivated with covalent H-terminations, leaving the individual DB activated on the tiny SiNW surface as the single H⁺ receptor. Single H⁺-DB interactions were directly detected by the SiNWFETs. On the basis of the detected single charge signals, both the kinetics of the single H⁺-DB interactions and the origin of the signal amplitude were systematically investigated. This work demonstrates a silicon nanosensor with unprecedented ability to investigate the physics of the solid/liquid interface at the single charge level, which holds great potential for future biochemical sensing applications.

MATERIALS AND METHODS

Device fabrication

The sub–10-nm gate oxide–free SiNWFETs were fabricated on 100-mm SOI wafers with standard Si process technology. The SOI wafers are composed of a 55-nm-thick lightly doped p-type Si layer on the top of a 145-nm-thick buried oxide (BOX). The top Si layer was thinned down from 55 to 30 nm by thermal oxidation and subsequent oxide etching with HF acid. An arsenic implantation was used to form the heavily n-doped (n⁺) source and drain terminals (S/D), while the channel region was protected by a photoresist during the implantation. The SiNWFET structure was defined by mixed lithography, i.e., the SiNW channels were pattered with a hydrogen silsesquioxane resist, while the large S/D pads were patterned with a UVN resist, followed by one-step reactive ion etching (RIE). The dopants in S/D were activated by rapid thermal processing at 1000°C for 10 s in N₂ atmosphere. To fully suspend the SiNW channel, the SOI wafers were dipped in 5% HF for 30 s to etch off 10 nm of the BOX. Afterward, thermal annealing was performed in H₂ atmosphere to enable sufficient surface Si atom reflow and therefore reparation of RIE-induced plasma damage on the SiNW channel surface. The H₂ annealing is performed in a temperature range of 800° to 880°C and a time range of 2 to 20 min. The actual annealing temperature and time depend on the SiNW channel geometry. To facilitate measurement with electrolyte, long Si (n⁺) leads were designed to connect S/D of the SiNWFETs to the contact pads at the edges of the chip, on which a 10-nm-thick nickel silicide layer was formed to further reduce series resistance. A photo resist layer was used as passivation for the S/D and leads to avoid excessive leakage current in electrolyte, while the SiNW channel region was exposed for sensing in electrolyte. Last, the wafers were dipped in BHF for 5 s to remove the native oxide on the SiNW channel.

Electrical measurements

A polydimethylsiloxane container was placed on top of the Si chip for holding the solution, in which a commercial AgCl/Ag reference electrode immersed into was set at a gate potential. Transfer (I_DS versus V_G) and output (I_DS versus V_DS) characteristics were measured at room temperature on a probe station using a Keysight B1500A precision semiconductor parameter analyzer. The PSD and high-frequency sampling of I_DS were characterized using a Keysight E4727A advanced low-frequency noise analyzer. For each measurement, at a fixed I_DS, V_DS was biased at 10 mV.

Calculation of potential and charge distribution at the SiNW/electrolyte interface

Our SiNWFET has a gate-all-around structure. Under inversion, the dependence of net charge density (σ_Si) inside the SiNW channel on Si surface potential (ψ_Si) can be expressed as

$${\mathrm{\sigma }}_{\text{Si}}=-\mathit{qr}(n_0{e}^{\frac{{\mathrm{\psi }}_{\text{Si}}}{\mathit{kT}}}+N_{\mathrm{A}})/\mathrm{\gamma }$$ (2)

Here, γ is a correction factor, i.e., γ = 0.978 + 1.72 × exp (0.0256 × ψ_Si), dependent on the SiNW channel geometry. Its detailed derivation can be found in section S16.

H⁺ concentrations at the Stern/diffuse layer interface and in the bulk solution, i.e., c_Hs and c_HCl, obey Boltzmann distribution (34)

$$c_{\text{Hs}}=c_{\text{HCl}}\text{exp}\left(\frac{q(V_{\mathrm{G}}-V_0-{\mathrm{\psi }}_{\text{dif}})}{\mathit{kT}}\right)$$ (3)

where ψ_dif is the potential at the Stern/diffuse layer boundary. To simplify the calculation, here, a constant term V₀ is introduced to sum up the potential drops across the reference electrode junction and the potential generated by the fixed charge on SiNW surface. Charge densities in the diffuse layer (σ_dif) and on the oxide surface (σ_ox) can be calculated using the site-bonding model through (34, 35)

$${\mathrm{\sigma }}_{\text{dif}}=\sqrt{8\mathit{kT}{\mathrm{\epsilon }}_{\mathrm{w}}{N}_{\text{Avo}}{c}_{\text{HCl}}}\text{sinh}\left(\frac{q(V_{\mathrm{G}}-V_0-{\mathrm{\psi }}_{\text{dif}})}{\mathit{kT}}\right)$$ (4)

$${\mathrm{\sigma }}_{\text{ox}}={\mathit{qN}}_{\text{OH}}\left(\frac{{c_{\text{Hs}}}^2-K_a{K}_b}{K_a{K}_b+K_b{c}_{\text{Hs}}+{c_{\text{Hs}}}^2}\right)$$ (5)

where ε_w is the dielectric constant of water, N_Avo is the Avogadro’s number, and K_a and K_b are the equilibrium constants of the surface reaction between Si─OH and H⁺. Meanwhile, σ_dif is also related to the Stern layer capacitance C_st through

$${\mathrm{\sigma }}_{\text{dif}}=({\mathrm{\psi }}_{\text{dif}}-{\mathrm{\psi }}_{\text{Si}})C_{\text{st}}$$ (6)

Last, charge neutrality requires

$${\mathrm{\sigma }}_{\text{ox}}+{\mathrm{\sigma }}_{\text{dif}}+{\mathrm{\sigma }}_{\text{Si}}=0$$ (7)

As the constant parameters V₀ and C_st are preset, potential and charge distribution can be solved by combining Eqs. 2 to 7. When V₀ = 60 mV and C_st = 4 × 10⁻⁵ F, the solved potential and charge distribution can fit the time constants in Figs. 3 and 4 quite well using Eq. 1. The extracted k_on and k_off are listed in table S1.

Supplementary Materials

This PDF file includes:

Supplementary Text

Figs. S1 to S14

Table S1

References