Figure 2.

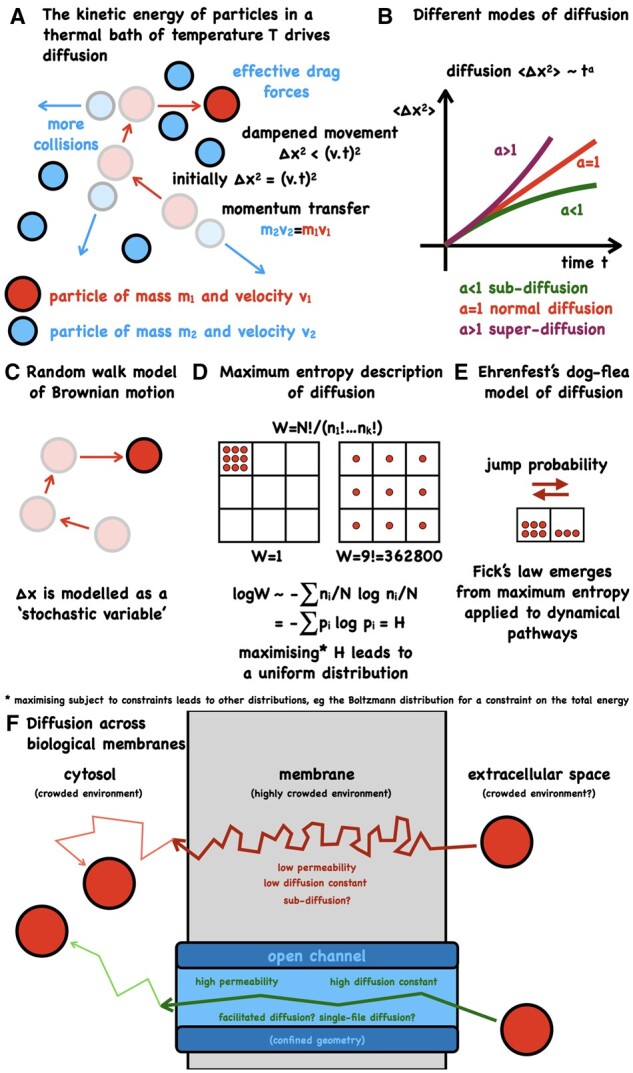
Diffusion is driven by thermal motion. (A) When particles collide they exchange momentum (mv with m=mass, v=velocity). The squared distance traveled by a particle moving with constant velocity is Δx² = (vt)². Frequent collisions between particles results in a short mean free path length, viscosity and drag, leading to any movement being dampened. (B) Free diffusion of a solute in a solvent results in the well-known linear dependence of the expectation of squared traveled distance with time, <Δx²> ∼ t, where the proportionality constant relates to the diffusion constant D. <Δx²> = 2 D t holds for diffusion in one dimension (this factor of 2 becomes 4 for two dimensional and 6 for three dimensional domains). Crowded environments, such as the cytosol, lead to nonlinear behavior and subdiffusion. Superdiffusion is associated with an active transport process. (C) The erratic behavior of a single particle (Brownian motion) can be reproduced well by a random walk and Monte-Carlo simulation is a popular approach for finding particle trajectories. Mathematical equations for describing molecular diffusion include the Langevin equation (microscopic) and Fick’s law (macroscopic). (D) Entropy considerations lead to correct predictions for reproducible macroscopic states. Boltzmann’s entropy characterizes the number of ways a microstate can be realized. Shown here is the problem of distributing numbers of particles n_i in different locations i. There is only one configuration in which all particles are in one defined location, whereas a uniform distribution can be achieved in many more ways. (E) Ehrenfest’s famous dog-flea model of diffusion. Particles (fleas) all have the same jump probability from one side to the other (from dog to dog). The number of trajectories from the side with a high number of particles is greater than the reverse movement, providing a simple explanation for why a net flux of particles down a concentration gradient emerges from undirected thermal motion. Computing expectation values for the trajectories (maximum entropy on the trajectories = maximum caliber) leads to Fick’s equation, revealing the inference nature of the phenomenological transport equations. (F) Diffusion across a membrane is likely to be confined, crowded and anomalous, depending on the particles’ route.