Identification of a circular code periodicity in the bacterial ribosome: origin of codon periodicity in genes?

ABSTRACT

Three-base periodicity (TBP), where nucleotides and higher order n-tuples are preferentially spaced by 3, 6, 9, etc. bases, is a well-known intrinsic property of protein-coding DNA sequences. However, its origins are still not fully understood. One hypothesis is that the periodicity reflects a primordial coding system that was used before the emergence of the modern standard genetic code (SGC). Recent evidence suggests that the X circular code, a set of 20 trinucleotides allowing the reading frames in genes to be retrieved locally, represents a possible ancestor of the SGC. Motifs from the X circular code have been found in the reading frame of protein-coding regions in extant organisms from bacteria to eukaryotes, in many transfer RNA (tRNA) genes and in important functional regions of the ribosomal RNA (rRNA), notably in the peptidyl transferase centre and the decoding centre. Here, we have used a powerful correlation function to search for periodicity patterns involving the 20 trinucleotides of the X circular code in a large set of bacterial protein-coding genes, as well as in the translation machinery, including rRNA and tRNA sequences. As might be expected, we found a strong circular code periodicity 0 modulo 3 in the protein-coding genes. More surprisingly, we also identified a similar circular code periodicity in a large region of the 16S rRNA. This region includes the 3ʹ major domain corresponding to the primordial proto-ribosome decoding centre and containing numerous sites that interact with the tRNA and messenger RNA (mRNA) during translation. Furthermore, 3D structural analysis shows that the periodicity region surrounds the mRNA channel that lies between the head and the body of the SSU. Our results support the hypothesis that the X circular code may constitute an ancestral translation code involved in reading frame retrieval and maintenance, traces of which persist in modern mRNA, tRNA and rRNA despite their long evolution and adaptation to the SGC.

Introduction

This work extends the results observed with the identification of circular code motifs in the ribosome [1]. The genetic code defines the set of rules needed to translate the information in DNA into proteins. Virtually all living organisms use the same standard genetic code (SGC) to determine how the 64 DNA trinucleotides (also known as codons) are translated into 20 amino acids and the stop signal. The degeneracy of the genetic code (most amino acids are coded by more than one codon) and specific codon usage bias in different organisms leads to a biased distribution of codons, and an intrinsic property of protein-coding DNA, known as three-base periodicity (TBP), defined as the preferential spacing of nucleotides and other n-tuples such as trinucleotides by distances of 3, 6, 9, etc. bases [2], i.e. a periodicity 0 modulo 3.

This periodic phenomenon has intrigued biologists for decades [e.g. ^3–5]. For example, it led to the proposal that the ancestral forms of present-day genes might have been coded by the primitive comma-free codes RRY and RNY (R= {A,G}, Y= {C,T}, N being any base) [6–8]. To illustrate the notion of TBP, for a RRY code, a word RRY|RRY|RRY| … implies that any letter Y is distant from another letter Y by a multiple of 3 letters (3, 6, etc.), and any trinucleotide RRY is also distant from another trinucleotide RRY by a multiple of 3 letters (0, 3, 6, etc.), etc. Obviously, in real genetic sequences, the preferential occurrence of some codons in genes (such as the $X$ circular code, defined below or the codon usage biases observed in different genomes) implies a modulo 3 periodic signal which is very noisy but which can be identified by sensitive statistical-signal analysis functions. It was also suggested that TBP may have a structural or functional role, for example to maintain the reading frame [9] or to regulate gene expression in some way [10,11]. Furthermore, powerful modern algorithms utilize the TBP to predict coding regions in unannotated genomes [12–18]. Unravelling the origins of TBP may help understand the forces that shaped the code during the early evolution of life on Earth. It has been suggested that TBP is simply due to species-specific amino acid or codon usage bias [8,19,20], although recently this has been shown to be insufficient to explain TBP in modern genes [21]. It has also been proposed that TBP additionally reflects a tendency for trinucleotides to cluster in the same phase [22]. In addition to TBP in protein-coding genes, a small number of studies have also identified periodicities in homologous regions of transfer RNA (tRNA) and ribosomal RNA (rRNA) genes [23–25], and some authors have concluded that this might reflect a primal pre-translational code [26].

One potential primordial translation code is the $X$ circular code [27]. According to coding theory, circular codes are a weaker version of comma-free codes, where any word written on a circle (the last letter becoming the first in the circle) has a unique decomposition into trinucleotides of the circular code. The mathematical formalisms (definitions, theorems, properties, enumeration, etc.) of codes, circular codes and a special class of circular codes, known as comma-free codes, can be found in two reviews [28,29], and are summarized here in Fig. 1. A circular code with words of 3 letters (e.g. trinucleotides) on a 4-letter alphabet (e.g. the genetic alphabet) is said to be maximal when it contains 20 words [27]. Indeed, there is no circular code with trinucleotides on the genetic alphabet that has a strictly larger size than 20 words. There are 12,964,440 maximal circular codes [27]. Remarkably, one of the maximal circular codes called the $X$ circular code, was found to be overrepresented in the reading frame of protein-coding genes from bacteria, archaea, eukaryotes, plasmids and viruses [27,30,31]. The $X$ circular code consists of 20 trinucleotides

$$\begin{array}{rl}& X=\{AAC,AAT,ACC,ATC,ATT,CAG,CTC,CTG,GAA,\\ & GAC,GAG,GAT,GCC,GGC,GGT,GTA,GTC,GTT,\\ & TAC,TTC\}\end{array}$$ (1)

Figure 1.

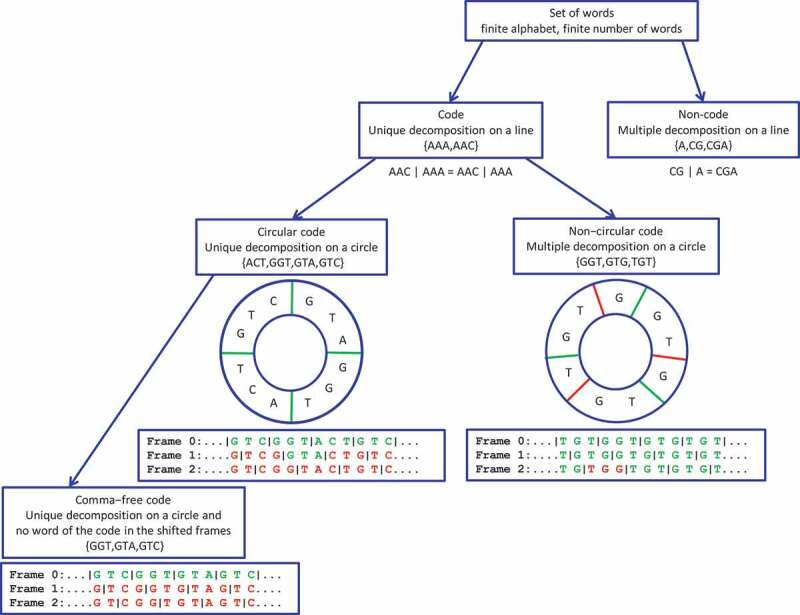
Hierarchy of a set of words, a code, a circular code and a comma-free code. The symbol ‘|’ denotes the decomposition on a line for a code or non-code, and on a circle for a code which is circular or non-circular. The set $\left\{AAA,AAC\right\}$ is a code as there is an unique decomposition on a line for any words of the code (an example of an unique decomposition on a line is given with the word $AACAAA$). The genetic code $\left\{AAA,\dots ,TTT\right\}$ is a code from a mathematical point of view. The frame 0 is the reading frame. Words belonging to the code are shown in green, and other words are in red. The code $\left\{ACT,GGT,GTA,GTC\right\}$ is circular, since only the frame 0 (reading frame) can be read by words of the code. There is an unique decomposition on a circle for any words of the circular code (an example of an unique decomposition on a circle is given with the word $GTAGGTACTGTC$; green symbol ‘|’). The code $\left\{GGT,GTG,TGT\right\}$ is not circular as several frames (here frames 0 and 1) can be read by words of the code (several decompositions on a circle; green and red symbols ‘|’). The code $\left\{GGT,GTA,GTC\right\}$ is comma-free, since words of the code appear only in the reading frame.

and codes the 12 following amino acids (three and one letter notation)

$$\mathcal{X}=\left\{Ala,Asn,Asp,Gln,Glu,Gly,Ile,Leu,Phe,Thr,Tyr,Val\right\}=\left\{A,N,D,Q,E,G,I,L,F,T,Y,V\right\}.$$ (2)

The trinucleotide set $X$ has several strong mathematical properties. In particular, it is self-complementary, i.e. 10 trinucleotides of $X$ are complementary to the other 10 trinucleotides of $X$, e.g. $AAC\in X$ is complementary to $GTT\in X$. Moreover, the +1/-2 and +2/-1 circular permutations of $X$, denoted $X_1$ and $X_2$ respectively, are also maximal circular codes ($C^3$) and are complementary to each other [27]. The class of circular codes, like comma-free codes, also have the property of synchronizability, i.e. they are hypothesized to retrieve and maintain the reading frame by using an appropriate window of nucleotides. In any sequence generated by a trinucleotide comma-free code, the reading frame can be determined in a window length of at most 3 consecutive nucleotides, while for the $X$ circular code, at most 13 consecutive nucleotides (i.e. at most 4 trinucleotides) are enough to always retrieve the reading frame. In other words, a sequence ‘motif’ containing several consecutive $X$ trinucleotides is sufficient to determine the correct reading frame (see Fig. 1 for examples).

The hypothesis of the $X$ circular code as a primordial coding system is supported by evidence from several statistical analyses of modern genomes. For example, it was shown in a large-scale study of 138 eukaryotic genomes [32] that $X$ motifs are found preferentially in protein-coding genes compared to non-coding regions with a ratio of ~8 times more $X$ motifs located in genes. More detailed studies of the complete gene sets of yeast and mammal genomes [33,34] confirmed the strong enrichment of $X$ motifs in genes and further demonstrated a statistically significant enrichment in the reading frame compared to frames 1 and 2 (p-value<10⁻¹⁰). In addition, it was shown that most of the mRNA sequences from these organisms (e.g. 98% of experimentally verified genes in S. cerevisiae) contain $X$ motifs.

In addition to mRNA sequences, conserved $X$ motifs have also been found in many tRNA genes [35], as well as many important functional regions of the ribosomal RNA, notably the decoding centre [1,36–38], which suggest their involvement in universal gene translation mechanisms. Intriguingly, the theoretical minimal RNA rings, short RNAs designed to code for all coding signals without coding redundancy among frames, are also biased for codons from the $X$ circular code [39]. These RNA rings, despite being designed based on coding constraints, attempt to mimic primitive tRNAs and potentially reflect ancient translation machineries [40,41]. Based on the combined results of these previous studies, we hypothesized that the $X$ circular code was an ancestor code of the SGC, which would have been used to code a smaller set of amino acids and with the additional ability to identify and maintain the reading frame. This primordial circular code would have existed before the emergence of complex start/stop codon recognition systems (see the model proposed in Fig. 8 in [1]), although the molecular mechanisms underlying this process are not known. It is also unknown whether circular codes continue to contribute to frame recognition in extant organisms that use the standard genetic code to code for highly complex proteins.

In this paper, we extend our study of the ribosome [1] and investigate whether the $X$ circular code, like the SGC, presents a periodicity property. To achieve this, we used a powerful circular code correlation function to search for periodicity patterns involving the 20 trinucleotides of the $X$ circular code in coding sequences and in the translation machinery, including rRNA and tRNA, from bacteria. As might be expected, we found a strong circular code periodicity in the coding regions. More surprisingly, we also identified a statistically significant circular code periodicity of $X$ trinucleotides in a large region of the 16S rRNA for a large set of >100 sequences from diverse bacteria.

Materials and methods

We define here a circular code correlation function which gives exact probabilities (with the exception of numerical approximations). This approach is particularly adapted to identifying periodicities in short and noisy sequences, such as the ribosomal and transfer RNAs.

Circular code correlation function

A language $F$, e.g. a genome or a set of genomes, consists of $\left|F\right|$ words, e.g. protein-coding genes, ribosomal RNA (rRNA) genes, etc., on the alphabet $B=\left\{A,C,G,T\right\}$ ($F$ is a finite subset of all words over $B$). Let $w=l_1{l}_2\dots l_{\left|w\right|}$ be a word of $F$ of length $\left|w\right|$ letters (nucleotides), $l_i\in B$ for $i\in \left\{1,\dots ,\left|w\right|\right\}$. Let $m$ and $m^{\prime }$ be 2 motifs of respective lengths $\left|m\right|$ et $\left|m^{\prime }\right|$ on $B$. Then, the word correlation function $A_{m,m^{\prime }}\left(i,w\right)$ in $w$ is defined by

$$A_{m,m^{\prime }}\left(i,w\right)=\frac{1}{l\left(w\right)}\sum _{p=1}^{l\left(w\right)}{\delta }_m\left(p\right)\cdot {\delta }_{m^{\prime }}\left(p+\left|m\right|+i\right),i=0,\dots ,imax$$ (3)

with

$${\delta }_m\left(p\right)=\left\{\begin{array}{c}1ifthemotifinpositionp..p+\left|m\right|-1ism\\ 0otherwise\end{array}\right.$$

and $l\left(w\right)=\left|w\right|-\left(\left|m{m}^{\prime }\right|+imax\right)+1$ with the length $\left|m{m}^{\prime }\right|$ $=\left|m\right|+\left|m^{\prime }\right|$.

Note that when $i=0$, the motif $m$ in position $p..p+\left|m\right|-1and$ the motif $m^{\prime }$ in position $p+\left|m\right|+i..p+\left|m\right|+i+$ $\left|m^{\prime }\right|-1$, i.e. $p+\left|m\right|..p+\left|m{m}^{\prime }\right|-1$, are consecutive.

This definition of $A_{m,m^{\prime }}\left(i,w\right)$ can also be understood as follows. Let an $i$-motif $m{N}^i{m}^{\prime }$ be 2 motifs $m$ and $m^{\prime }$ separated by $i$, $i\in \left\{0,\dots ,imax\right\}$, any letters $N\in B$. In order to count the occurrences of $m{N}^i{m}^{\prime }$ in a word $w$ of $F$ under the same conditions for all $i\in \left\{0,\dots ,imax\right\}$, i.e. without probability bias, only the $l\left(w\right)=\left|w\right|-\left(\left|m{m}^{\prime }\right|+imax\right)+1$ first letters of $w$ are analysed (a few $i$-motifs at the end of the sequence are thus not considered, since $l\left(w\right)$ is a function of $imax$ and not of $i$). Indeed, when $p=l\left(w\right)$ and $i=imax$, then the motif $m^{\prime }$ in position $p+\left|m\right|+i=\left|w\right|-\left|m^{\prime }\right|+1$ has its last letter $l_{\left|m^{\prime }\right|}$ in the last position of $w$.

1. The definition of $A_{m,m^{\prime }}\left(i,w\right)$ is a generalization of the classical letter correlation function used in signal analysis when the motifs $m$ and $m^{\prime }$ are letters, i.e. when $m=l$ and $m^{\prime }=l^{\prime }$ (see Appendix A).

2. As a consequence of Equation (3), the word correlation function $A_{m,m^{\prime }}\left(i,w\right)$ gives exact probabilities (with the exception of numerical approximations) which can be retrieved mathematically when the word $w$ has a basic structure or a combination of basic structures, e.g. $l^n$, ${\left(l_1{l}_2\right)}^n$, ${\left(l_1{l}_2\right)}^n{\left(l_1{l}_2{l}_3\right)}^m$, etc. (see Appendix A and in particular, the example computations in A.3). However, only a computed function $A_{m,m^{\prime }}\left(i,w\right)$ can be used in real genetic sequences.

3. As consequences of the two previous remarks, the function $A_{l,l^{\prime }}\left(i,w\right)$ (particular case when $m=l$ and $m^{\prime }=l^{\prime }$) is similar but not identical to the classical correlation function which is in bijection with the Fourier transform. Indeed, the classical correlation function does not correct the side effect induced by the finite length of the word $w$ (see Appendix A and in particular, the example computations in A.3).

In order to study the correlation function of the circular code $X$ based on 20 trinucleotides, we choose $\left|m\right|=\left|m^{\prime }\right|=3$ and extend Equation (3) to a set of motifs. Let $B^3=\left\{AAA,\dots ,TTT\right\}$ be the set of the 64 trinucleotides with the following partition into 2 classes $C_2=\{X,\overline{X}:X{\cap }^{}\overline{X}=\varnothing ,$ $X\cup \overline{X}=B^3\}$ by recalling $X=\{AAC,AAT,ACC,ATC,ATT,$

$CAG,CTC,CTG,GAA,GAC,GAG,GAT,GCC,GGC,GGT,$ $GTA,GTC,GTT,$ $TAC,TTC\}$ which was given in Equation (1). Then, the circular code autocorrelation function $A_{X,X}\left(i,w\right)$ in $w$ is defined by

$$A_{X,X}\left(i,w\right)=\sum _{m\in X}\sum _{m^{\prime }\in X}{A}_{m,m^{\prime }}\left(i,w\right),i=0,\dots ,imax$$ (4)

with $A_{m,m^{\prime }}\left(i,w\right)$ defined in Equation (3).

Equation (4) is easily extended to a language. Thus, the circular code autocorrelation function $A_{X,X}\left(i,F\right)$ in $F$ is defined by

$$A_{X,X}\left(i,F\right)=\frac{1}{\left|F\right|}\sum _{w\in F}{A}_{X,X}\left(i,w\right),i=0,\dots ,imax$$ (5)

with $A_{X,X}\left(i,w\right)$ defined in Equation (4).

The function $i\to A_{X,X}\left(i,F\right)$, which gives the occurrence probability that the circular code $X$ appears any $i$ letters $N$ after $X$ in the language $F$, is called the circular code autocorrelation function $X{N}^{i}X$ (associated with the $i$-motif $X{N}^{i}X$ based on the circular code $X$). It is represented by a curve with:

– on the abscissa, the number $i$ of letters $N$ between $X$ and itself (i.e. $X$ and $X$), $i$ varying from 0 to $imax$, which is chosen to be equal to 20 in the described results.

– on the ordinate, the occurrence probability $A_{X,X}\left(i,F\right)$ of $X{N}^{i}X$ in $F$.

1. ${\sum }_{m\in \left\{X,\bar{X}\right\}}{\sum }_{m^{\prime }\in \left\{X,\bar{X}\right\}}{A}_{m,m^{\prime }}\left(i,F\right)=1$ for all $i$ letters $N^i$, $i\in \left\{0,\dots ,imax\right\}$, and any $F$. The curve $A_{X,X}\left(i,F\right)$ is a horizontal line of value 1.

2. $A_{X,X}\left(i,F\right)=\frac{20\cdot 20}{64\cdot 64}=\frac{25}{256}\approx 0.0977$ for all $i$ letters $N^i$, $i\in \left\{0,\dots ,imax\right\}$, in a random language $F$, and in particular in a random word (sequence) $w$ (case $\left|F\right|=1$). The curve $A_{X,X}\left(i,F\right)$ is a horizontal line of value $0.0977$. $A_{X,X}\left(i,F\right)=\frac{20\cdot 20}{61\cdot 61}\approx 0.107$ for all $i$ letters $N^i$, $i\in \left\{0,\dots ,imax\right\}$, in a random language $F$ without the three stop codons.

Remark 2 is particularly interesting as any correlation curve without horizontal line can be associated with a non-random language $F$ or a non-random word (sequence) $w$.

In Appendix A, we compare the method developed here with the two classical correlation functions used in signal analysis.

Protein-coding genes

Bacterial protein-coding genes were obtained from the GenBank database (http://www.ncbi.nlm.nih.gov/genome/browse/). Only one genome for each species was selected. Genes without initiation codons, without stop codons, with nucleotides different from $B$ and with lengths non-modulo 3 were excluded. This resulted in a set of bacterial genes $F=\mathrm{G}\mathrm{e}\mathrm{n}\mathrm{e}{\mathrm{s}}_{\mathrm{B}\mathrm{a}\mathrm{c}}$ containing 465,762 genes with a total length of 2,339,752,707 trinucleotides.

Ribosomal RNA sequences and structure

Multiple sequence alignments for 16S small subunit (SSU) rRNAs and 23S large subunit (LSU) rRNAs were obtained from the Comparative RNA Web (CRW) site at http://www.rna.icmb.utexas.edu/DAT/3C/Alignment. In order to obtain a broad but sparse sampling of the bacterial domain, we used the seed alignment containing complete sequences for rRNAs from bacteria, and selected 1 representative sequence from each subgroup. This resulted in two alignments, each containing 103 sequences from the organisms provided in the Appendix B. Each alignment was then divided into two equal parts, corresponding to the 5ʹ and 3ʹ regions of the ribosome sequences. For the 16S rRNA alignment, the 3ʹ region corresponds to nucleotides 1–765 (E. coli numbering) and the 5ʹ region corresponds to nucleotides 766–1530 (E. coli numbering). For the 23S rRNA alignment, the 5ʹ region corresponds to nucleotides 1–1447 (E. coli numbering) and the 3ʹ region corresponds to nucleotides 1448–2895 (E. coli numbering).

The secondary structures of the SSU rRNA for E. coli were downloaded from http://apollo.chemistry.gatech.edu/RibosomeGallery/. Mapping of information on to secondary structures was performed with RiboVision (apollo.chemistry.gatech.edu/RiboVision) [42]. Coordinates of the high-resolution crystal structure of the T. thermophilus ribosome (PDB entry 4W2F) were obtained from the PDB database (https://www.rcsb.org/). This was chosen because it contains mRNA nucleotides and three deacylated tRNAs in the A, P and E sites. Numbering of the T. thermophilus SSU rRNA is the same as for E. coli. Visualization and analysis of the three-dimensional structures, as well as image preparation were performed with PyMOL (The PyMOL Molecular Graphics System, Version 1.2r3pre, Schrödinger, LLC).

Transfer RNA sequences

Transfer RNA (tRNA) sequences were downloaded from the tRNAdb database at http://trna.bioinf.uni-leipzig.de. All bacterial sequences were selected and grouped according to the corresponding amino acids. This resulted in 20 sets of tRNA sequences corresponding to each amino acid, with the number of sequences in each set given in the Appendix B.

Results

Circular code periodicity in bacterial genes

We first applied the circular code autocorrelation method to a large set of bacterial genes $F=\mathrm{G}\mathrm{e}\mathrm{n}\mathrm{e}{\mathrm{s}}_{\mathrm{B}\mathrm{a}\mathrm{c}}$ (see Method). As shown in Fig. 2, the values of the function $A_{X,X}\left(i,\mathrm{G}\mathrm{e}\mathrm{n}\mathrm{e}{\mathrm{s}}_{\mathrm{B}\mathrm{a}\mathrm{c}}\right)$ are higher for multiples $\left(3i\right)$ where $i\in \left\{0,1,2\dots \right\}$ than for multiples of $\left(3i+1\right)$or $\left(3i+2\right)$, indicating that a circular code periodicity 0 modulo 3 is present in the genes for the circular code $X$. Note that the average values are around 0.1 as expected by Remark 2. While this result is new for a circular code, the observation of three base periodicity in genes of eukaryotes, bacteria, viruses, chloroplasts and mitochondria is classical and has been described in the past by several authors using different methods, in particular at the sequence level by Shepherd [2,15] and at the population level by Fickett [43], Michel [44] Fig. 1 and Arquès and Michel [3,45–47].

Figure 2.

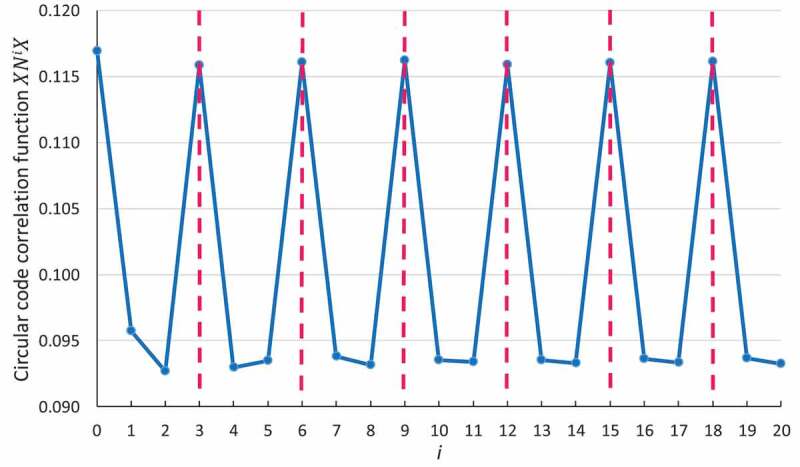
Circular code periodicity 0 modulo 3 identified by the circular code autocorrelation function $A_{X,X}\left(i,\mathrm{G}\mathrm{e}\mathrm{n}\mathrm{e}{\mathrm{s}}_{\mathrm{B}\mathrm{a}\mathrm{c}}\right)$ in bacterial genes. The abscissa represents the number $i$ of letters $N$ between $X$ and itself (i.e. $X$ and $X$), $i$ varying from 0 to $imax=20$. The ordinate gives the occurrence probability $A_{X,X}\left(i,\mathrm{G}\mathrm{e}\mathrm{n}\mathrm{e}{\mathrm{s}}_{\mathrm{B}\mathrm{a}\mathrm{c}}\right)$ (Equation (5)) of $X{N}^{i}X$ in $\mathrm{G}\mathrm{e}\mathrm{n}\mathrm{e}{\mathrm{s}}_{\mathrm{B}\mathrm{a}\mathrm{c}}$.

Circular code periodicity in bacterial ribosomes

Next, we applied the circular code autocorrelation method to the 23S and 16S rRNA sequences from 103 bacterial organisms. In an initial study, we used the full-length rRNA sequences; however, no periodicity was observed (data not shown). Therefore, we divided the sequences into two parts corresponding to the 5ʹ and 3ʹ regions of each sequence, and calculated the circular code correlation functions for each region independently (Fig. 3). Although no periodicity is identified in the 5ʹ and 3ʹ regions of the 23S rRNA (Fig. 3A, B respectively) or the 5ʹ region of the 16S rRNA (Fig. 3C), we report these negative results in order to highlight the unicity of the circular code periodicity in the 3ʹ region of the 16S rRNA (Fig. 3D).

Figure 3.

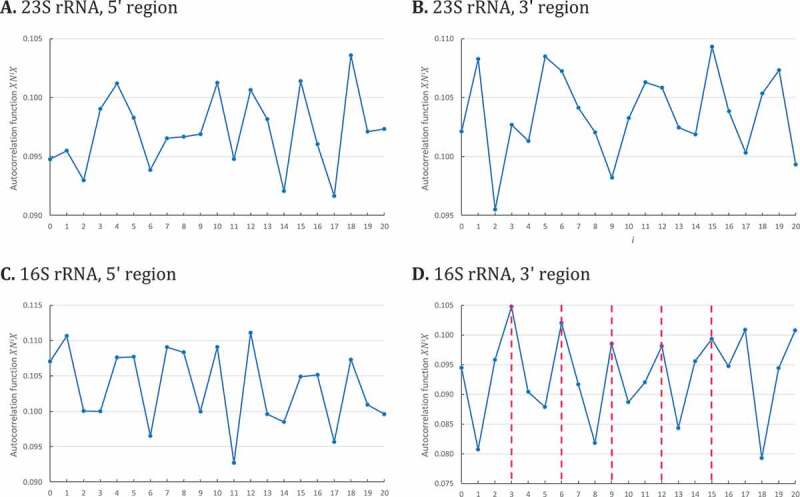
Circular code autocorrelation functions for bacterial 23S and 16S rRNA. The abscissa represents the number $i$ of letters $N$ between $X$ and itself (i.e. $X$ and $X$), $i$ varying from 0 to $imax=20$. The ordinate gives the occurrence probability $A_{X,X}\left(i,\mathrm{F}\right)$ (Equation (5)) of $X{N}^{i}X$ in $\mathrm{F}$. A. Circular code autocorrelation function $A_{X,X}\left(i,23\mathrm{S}\mathrm{r}\mathrm{R}\mathrm{N}{\mathrm{A}}_{1-1447}\right)$ in the 5ʹ region (1–1447) of 23S bacterial rRNA. B. Circular code autocorrelation function $A_{X,X}\left(i,23\mathrm{S}\mathrm{r}\mathrm{R}\mathrm{N}{\mathrm{A}}_{1448-2895}\right)$ in the 3ʹ region (1448–2895) of 23S rRNA. C. Circular code autocorrelation function $A_{X,X}\left(i,16\mathrm{S}\mathrm{r}\mathrm{R}\mathrm{N}{\mathrm{A}}_{1-765}\right)$ in the 5ʹ region (1–765) of 16S rRNA. D. Circular code autocorrelation function $A_{X,X}\left(i,16\mathrm{S}\mathrm{r}\mathrm{R}\mathrm{N}{\mathrm{A}}_{766-1530}\right)$ in the 3ʹ region (766–1530) of 16S rRNA, revealing the circular code periodicity 0 modulo 3.

For the first time, the circular code correlation function $A_{X,X}\left(i,16\mathrm{S}\mathrm{r}\mathrm{R}\mathrm{N}{\mathrm{A}}_{766-1530}\right)$ identifies a circular code periodicity 0 modulo 3 (up to $i=15$) in the 3ʹ region (766–1530) of bacterial 16S rRNA (Fig. 3D). Obviously, since the 3ʹ regions of $16\mathrm{S}\mathrm{r}\mathrm{R}\mathrm{N}\mathrm{A}$ are relatively short, this modulo 3 periodicity is not regular compared to the one observed in genes (compared to Fig. 2). However, an elementary calculus proves that this periodicity 0 modulo 3 is significant. Indeed, the probability that $A_{X,X}\left(0,{\text{16SrRNA}}_{\text{766-1530}}\right)A_{X,X}(1,\text{16SrRN}$ ${\text{A}}_{\text{766-1530}})$ is equal to $1/2$. The probability that $A_{X,X}\left(i,16\mathrm{S}\mathrm{r}\mathrm{R}\mathrm{N}{\mathrm{A}}_{766-1530}\right)>A_{X,X}\left(i-1,16\mathrm{S}\mathrm{r}\mathrm{R}\mathrm{N}{\mathrm{A}}_{766-1530}\right)$ and $A_{X,X}\left(i,16\mathrm{S}\mathrm{r}\mathrm{R}\mathrm{N}{\mathrm{A}}_{766-1530}\right)>A_{X,X}\left(i+1,16\mathrm{S}\mathrm{r}\mathrm{R}\mathrm{N}{\mathrm{A}}_{766-1530}\right)$ with $i\equiv 0\left(\mathrm{m}\mathrm{o}\mathrm{d}3\right)$ and $i>0$ is equal to $1/3$. By assuming independence between the events, the probability of a periodicity 0 modulo 3 until $i=15$ is equal to $P=\frac{1}{2}\cdot {\left(\frac{1}{3}\right)}^5\approx 0.002$.

The circular code periodicity 0 modulo 3 identified in the 3ʹ region of 16S rRNA leads to a direct biological conclusion: a unit of genetic information based on trinucleotides exists in the 3ʹ region of 16S rRNA, similarly to the protein-coding genes.

Circular code periodicity in the bacterial tRNA of alanine

We also applied the same correlation function in a large set of bacterial tRNA genes corresponding to the 20 amino acids (see Method). For the first time, the circular code autocorrelation function $A_{X,X}\left(i,\mathrm{t}\mathrm{R}\mathrm{N}{\mathrm{A}}_{\mathrm{A}\mathrm{l}\mathrm{a}}\right)$ identifies a circular code periodicity 0 modulo 3 (up to $i=12$) in the tRNA of alanine (Fig. 4). Obviously, this modulo 3 periodicity is noisy as the t$\mathrm{R}\mathrm{N}\mathrm{A}$ has a short length and constrained 2D and 3D structures. However, the calculus developed in the previous section proves that this periodicity 0 modulo 3 is significant and equal to $P=\frac{1}{2}\cdot {\left(\frac{1}{3}\right)}^4\approx 0.006$.

Figure 4.

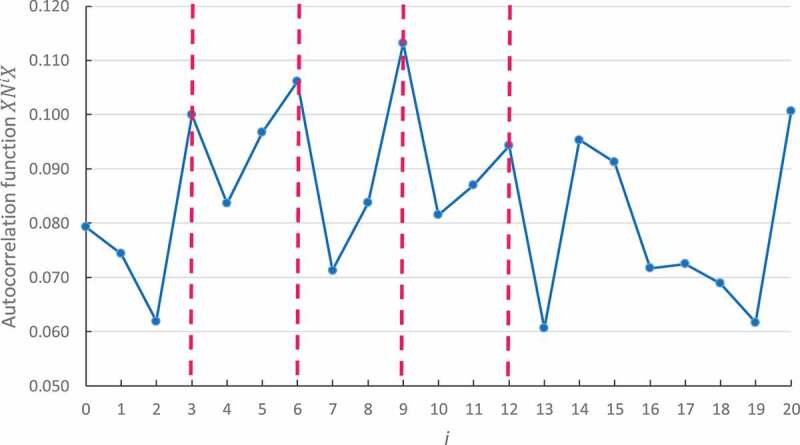
Circular code periodicity 0 modulo 3 identified by the circular code autocorrelation function $A_{X,X}\left(i,\mathrm{t}\mathrm{R}\mathrm{N}{\mathrm{A}}_{\mathrm{A}\mathrm{l}\mathrm{a}}\right)$ in the bacterial tRNA of alanine. The abscissa represents the number $i$ of letters $N$ between $X$ and itself (i.e. $X$ and $X$), $i$ varying from 0 to $imax=20$. The ordinate gives the occurrence probability $A_{X,X}\left(i,\mathrm{t}\mathrm{R}\mathrm{N}{\mathrm{A}}_{\mathrm{A}\mathrm{l}\mathrm{a}}\right)$ (Equation (5)) of $X{N}^{i}X$ in $\mathrm{t}\mathrm{R}\mathrm{N}{\mathrm{A}}_{\mathrm{A}\mathrm{l}\mathrm{a}}$.

No modulo 3 periodicity is observed in the 19 remaining tRNAs. To date, we have no explanation for the absence of this signal property in the other tRNAs and additional studies will have to be considered in the future.

Structural and functional analysis of circular code periodicity in 16S rRNA

Modern ribosomes are highly sophisticated molecular machines, consisting of two subunits that come together during the initiation of protein synthesis, remain together as individual amino acids are added to the growing peptide, and finally separate again in conjunction with the release of the finished protein [48]. Each subunit is a large nucleoprotein complex. In bacteria, the large subunit (LSU) contains the 23S rRNA and 5S rRNA, whereas the 16S rRNA makes up the bulk of the small subunit (SSU). The 16S rRNA is important for subunit association and translational accuracy. It consists of 1542 bases and the structural arrangement creates a 5ʹ domain, central domain, 3ʹ major domain, and 3ʹ minor domain.

As illustrated in Fig. 5, the observed circular code periodicity (0 modulo 3) in the 3ʹ region (766–1530) of bacterial 16S rRNA covers part of the central domain (helices h24-h27), all of the 3ʹ major domain (helices h28-h43) and part of the 3ʹ minor domain (helix h44). Notably, the 3ʹ major domain contains the decoding centre and interacts with both tRNA and mRNA. The decoding centre is widely accepted to be an essential building block of the primaeval ‘proto-ribosome’ that was already present in the Last Universal Common Ancestor (LUCA) [49,50], where it may have simply been a location to bind RNAs in an open structure configuration [51].

Figure 5.

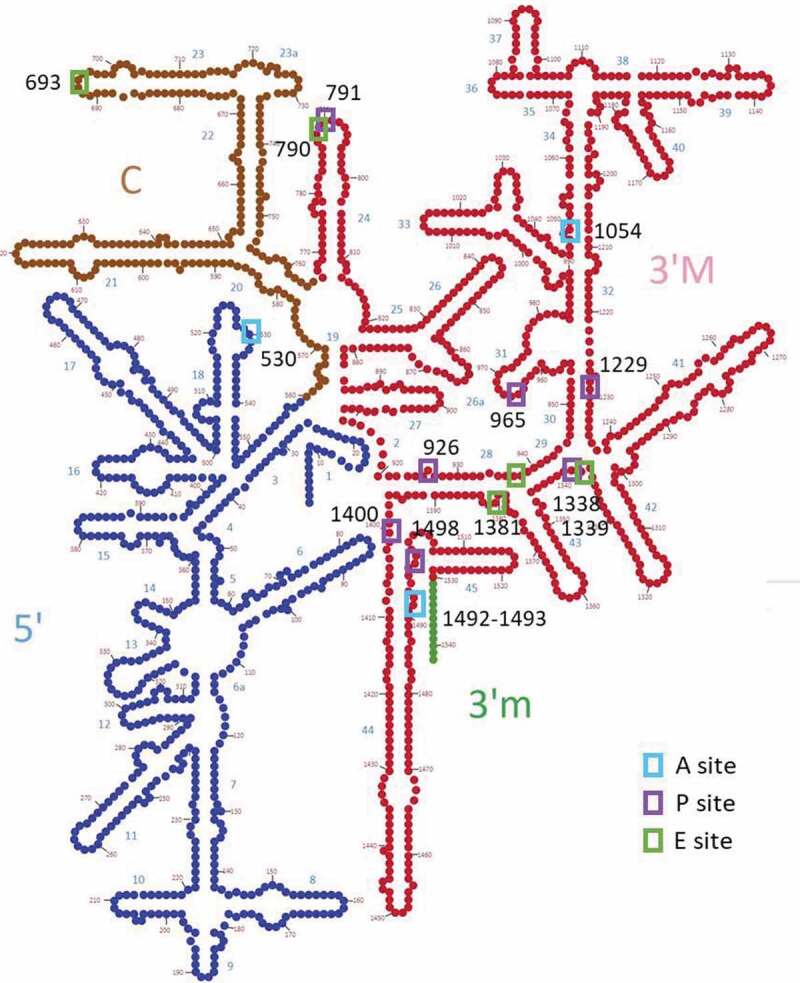
Schema of the 2D structure of the bacterial 16S rRNA (E. coli), showing the classical division into 4 domains: 5ʹ domain, central domain (C), 3ʹ major (M) and 3ʹ minor (m) domains. Interaction sites with tRNA are indicated by coloured boxes, and numbering is according to E. coli sequence. The region shown in red corresponds to the sequence segment with the circular code periodicity (0 modulo 3).

The spatial organization of the circular code periodicity is shown in Fig. 6. The periodicity is mainly localized in the SSU close to the interaction sites with the mRNA and tRNAs, but also extends into the body, along with the interface with the LSU formed by helix 44 in the 3ʹ minor domain (Fig. 6A). No periodicity was observed in the LSU. Within the SSU, the periodicity region covers all of the head (formed by the 3ʹ major domain), and part of the central domain that forms the platform (Fig. 6B). The mRNA and tRNAs lie across the neck (h28) of the SSU between the platform and the head. Finally, Fig. 6C,D shows the nucleotides close to the mRNA (<15 Å) and highlight the close packing of the periodicity around the decoding centre, with 102 out of 134 (76%) 16S nucleotides within the periodicity region.

Figure 6.

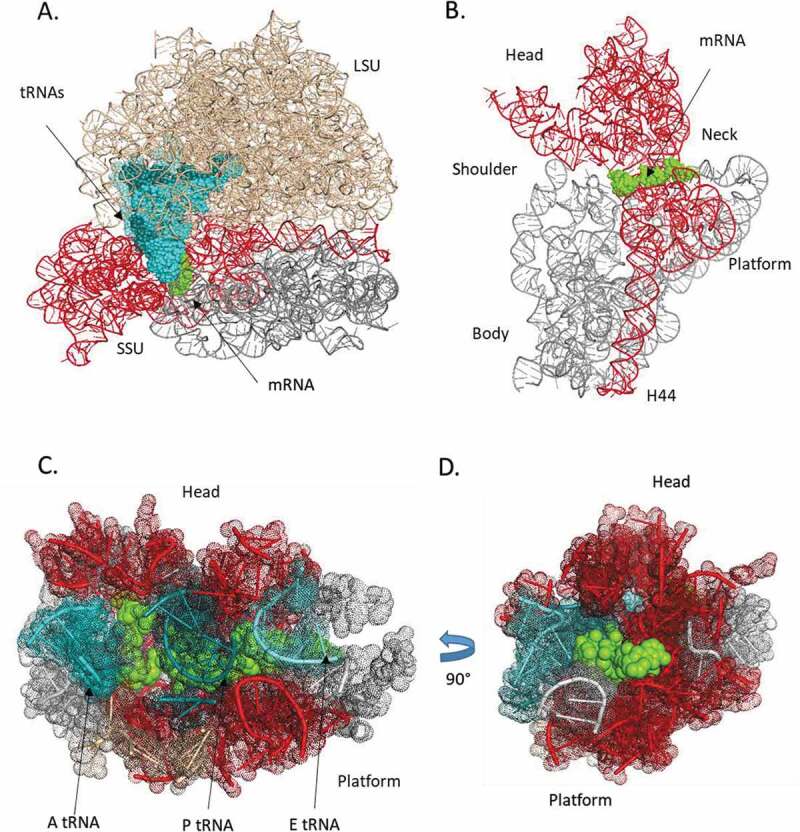
3D structure of the bacterial ribosome (E. coli). A. rRNA of the LSU (beige) and SSU (grey), the region (red) with the circular code periodicity (0 modulo 3), the mRNA segment (green), and the A-site (cyan), P-site (deep teal) and E-site tRNAs (light teal). B. SSU rRNA (grey) with the periodicity region (red) and the mRNA segment (green). The mRNA lies across the neck of the SSU between the platform and the head. C. Nucleotides close to the mRNA (<15 Å) with the tRNAs (coloured as in A), SSU RNA (grey) and periodicity region (red). D has been rotated 90° with respect to C.

Discussion

We have developed a new method that allows us to calculate exact probabilities of observing circular code autocorrelation, even for sequences with short lengths (as demonstrated in Appendix A). Using this method, we confirmed that the 20 trinucleotides of the $X$ circular code present a periodicity 0 modulo 3 in the protein-coding regions of bacterial genomes. Furthermore, for the first time, we identify three base periodicity in ribosomal RNA sequences. This would imply that the trinucleotide may be a fundamental unit of information within rRNA sequences, and is line with numerous previous studies showing that some rRNA sequences contain protein-coding genes [reviewed in ⁵²].

Importantly, the observed periodicity is restricted to the 3ʹ region of the 16S rRNA, which contains the decoding centre and other interaction sites with the mRNA and tRNAs in A, P and E sites. Our 3D structural analysis shows that the periodicity region surrounds the mRNA channel between the head and the body of the SSU. Previously, we showed that this region contains a number of $X$ motifs that are universally conserved in bacteria, but are also present in archaea and eukaryotic rRNA sequences [1]. This leads us to the question: do the $X$ motifs in the 16S rRNA interact somehow with $X$ motifs in the mRNA of protein-coding genes to regulate translation? Other mRNA–rRNA interactions are known to affect translation efficiency or quality. For example, hybridization between the Shine-Dalgarno sequence in the 5ʹ UTR of bacterial mRNA and the anti-Shine-Dalgarno region of the 16S rRNA directs the ribosome to the start codon of the mRNA [53]. Additional examples of mRNA–rRNA interactions include non-Shine-Dalgarno ribosome binding sites in the 5ʹ UTR [54], internal Shine-Dalgarno sequences [55] or recoding signals that direct ribosomal frameshifting [56].

The periodicity property in the 16S 3ʹ region largely corresponds to the ‘proto-SSU’ that has been proposed to represent the primordial ribosomal SSU [49,50,57,58]. Thus, our results provide additional support for the hypothesis that the primordial coding system was RNA-based, and this RNA translation template then evolved to form the modern tRNA, mRNA and rRNA sequences [59,60]. According to this theory, the initial replicator whose biomolecular activity initiated Darwinian evolution on Earth [61,62] consisted of short RNA oligonucleotides and was probably stabilized by small peptides containing amino acids such as glycine, alanine, aspartic acid or valine [63–65]. Necessary features of such an RNA translation template include some level of specificity between nucleotide triplets and the amino acids [66], and self-complementarity between nucleotides to allow replication [67]. The mathematical properties of the $X$ circular code meet these requirements: (i) it provides a mapping between trinucleotides and the early amino acids, (ii) it is circular and has the capacity to detect the reading frame, and (iii) it is self-complementary. Therefore, it is tempting to speculate that the TBP in protein-coding genes arose from the periodicity property of the $X$ circular code in the primordial ribosome.

Finally, the circular code autocorrelation function also allowed us to identify a circular code periodicity in the tRNA of alanine. The link between tRNAs and rRNAs has been highlighted by other groups and it is widely believed that rRNAs may have evolved by concatenation of tRNA-like molecules [e.g. ^{51, 58}]. It is noteworthy that alanine, along with glycine, is generally predicted to be one of the most ancient amino acids to be included in the genetic code [68,69]. Furthermore, we previously proposed that the comma-free code {GGC, GCC} was used initially to code Ala and Gly, and that this code quickly evolved to circular codes that included more and more amino acids [1]. A more in-depth study of TBP in tRNA sequences is planned in the near future to determine whether a weaker periodicity property remains to be found in the tRNAs coding for other amino acids.

Appendix A.

We compare the circular code autocorrelation method developed here (Equations (3) and (5)) with the two classical correlation methods used in Fourier analysis. After recalling these classical formulas, we extend them to an $i$-motif $m{N}^i{m}^{\prime }$, i.e. 2 motifs $m$ and $m^{\prime }$ separated by $i$, $i\in \left\{0,\dots ,imax\right\}$, any letters $N\in B$.

• (1) Classical correlation methods

The power spectral density is the Fourier transform of the correlation function which is classically estimated in a discrete signal on a word $w=l_1{l}_2\dots l_{\left|w\right|}$ according to

$${\hat{A}}_{l,l}\left(i,w\right)=\frac{1}{\left|w\right|}\sum _{p=1}^{\left|w\right|-i}{\delta }_l\left(p\right)\cdot {\delta }_l\left(p+i\right),i=0,\dots ,\left|w\right|-1$$ (6)

where

$${\delta }_l\left(p\right)=\left\{\begin{array}{c}1iftheletterinpositionpisl\\ 0otherwise\end{array}\right..$$

This estimate ${\hat{A}}_{l,l}\left(i,w\right)$ is so-called ‘biased’, because when the correlation lag $i$ approaches the length $\left|w\right|$, it differs from the exact probability calculus. The estimate ${\hat{A}}_{l,l}\left(i,w\right)$ has some drastic effects with short words (see the examples in Section A.3). Thus, another estimate is also proposed by normalizing the denominator

$${\widehat{A^{\prime }}}_{l,l}\left(i,w\right)=\frac{1}{\left|w\right|-i}\sum _{p=1}^{\left|w\right|-i}{\delta }_l\left(p\right)\cdot {\delta }_l\left(p+i\right),i=0,\dots ,\left|w\right|-1$$ (7)

where ${\delta }_l\left(p\right)$ is defined in Equation (6).

While this estimate ${\widehat{A^{\prime }}}_{l,l}\left(i,w\right)$ gives exact probability calculus with long words, it becomes less accurate with short words (see the examples in Section A.3).

• (2) Extension of classical correlation methods to an $i$-motif

In order to compare Equation (6) with Equation (3) associated with the $i$-motif $X{N}^{i}X$, we omit the Fourier case $i=0$ and we trivially extend Equation (6) to an $i$-motif $m{N}^i{m}^{\prime }$ separated by $i$ any letters $N\in B$

$$\begin{array}{rl}& {\hat{B}}_{m,m^{\prime }}\left(i,w\right)=\frac{1}{\left|w\right|-\left|m{m}^{\prime }\right|+1}\sum _{p=1}^{\left|w\right|-i-\left|m{m}^{\prime }\right|+1}{\delta }_m\left(p\right)\\ & \cdot {\delta }_{m^{\prime }}\left(p+\left|m\right|+i\right),i=0,\dots ,\left|w\right|-\left|m{m}^{\prime }\right|\end{array}$$ (8)

where ${\delta }_m\left(p\right)$ and $\left|m{m}^{\prime }\right|$ are defined in Equation (3).

Note that the case $i=0$ does not have the same meaning for the Equations (6) and (8). Similarly, Equation (7) is extended to an $i$-motif $X{N}^{i}X$ as follows:

$$\begin{array}{rl}& {{\hat{B}}^{\prime }}_{m,m^{\prime }}\left(i,w\right)=\frac{1}{\left|w\right|-i-\left|m{m}^{\prime }\right|+1}\sum _{p=1}^{\left|w\right|-i-\left|m{m}^{\prime }\right|+1}{\delta }_m\left(p\right)\\ & \cdot {\delta }_{m^{\prime }}\left(p+\left|m\right|+i\right),i=0,\dots ,\left|w\right|-\left|m{m}^{\prime }\right|\end{array}$$ (9)

where ${\delta }_m\left(p\right)$ and $\left|m{m}^{\prime }\right|$ are defined in Equation (3).

Equation (8) (not shown for Equation (9)) easily extends to a sequence population $F$ as follows:

$${\hat{B}}_{m,m^{\prime }}\left(i,F\right)=\frac{1}{\left|F\right|}\sum _{w\in F}{\hat{B}}_{m,m^{\prime }}\left(i,w\right),i=0,\dots ,\left|w\right|-1$$ (10)

(3) Application examples

We give computation examples of the correlation function $A_{m,m^{\prime }}\left(i,w\right)$ on the sequences ${\left(RRY\right)}^{+}$ and ${\left(RNY\right)}^{+}$ by choosing, for sake of simplicity, the letters $m=m^{\prime }=R$ on the 2-letter alphabet $B^{\prime }=\left\{R,Y\right\}$ ($N=\left\{R,Y\right\}$).

• (1) Sequence $\mathit{w}={\left(RRY\right)}^{+}$

In this first example, we apply the correlation function $A_{R,R}\left(i,w\right)$ on the sequence $w={\left(RRY\right)}^{+}=RRYRRY\dots$

(i) Exact calculus of ${\mathrm{A}}_{\mathrm{R},\mathrm{R}}\left(\mathrm{i},{\left(\mathrm{R}\mathrm{R}\mathrm{Y}\right)}^{+}\right)$ leads trivially to the following solution

$${\mathrm{A}}_{\mathrm{R},\mathrm{R}}\left(\mathrm{i},{\left(\mathrm{R}\mathrm{R}\mathrm{Y}\right)}^{+}\right)=\left\{\begin{array}{c}\frac{1}{3}\approx 0.3333\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{i}\equiv 0\left(\mathrm{m}\mathrm{o}\mathrm{d}3\right)\\ \frac{1}{3}\approx 0.3333fori\equiv 1\left(mod3\right)\\ \frac{2}{3}\approx 0.6667fori\equiv 2\left(mod3\right)\end{array}\right..$$

(ii) The computation of $A_{R,R}\left(i,{\left(RRY\right)}^n\right)$ (Equation (3)) in a simulated sequence of $n=33$ consecutive trinucleotides $RRY$ is associated with the exact probabilities (Table A1 and Fig. A1(A)).

Table A1.

Correlation function $A_{R,R}\left(i,{\left(RRY\right)}^n\right)$ in a simulated sequence ${\left(RRY\right)}^n$ of trinucleotide length $n\in \left\{33,333,3333\right\}$ where $i$ represents the number of letters $N$ between $R$ and itself, $i$ varying from 0 to $imax=7$, and $A_{R,R}\left(i,{\left(RRY\right)}^n\right)$ of $R{N}^{i}R$ in ${\left(RRY\right)}^n$ is computed according to $A_{R,R}\left(i,{\left(RRY\right)}^{33}\right)$ (Equation (3)) and ${\widehat{B^{\prime }}}_{R,R^{\prime }}\left(i,{\left(RRY\right)}^n\right)$ (Equation (9)).

$i$	Equation (3) with ${\left(RRY\right)}^{33}$	Equation (9) with ${\left(RRY\right)}^{33}$	Equation (9) with ${\left(RRY\right)}^{333}$	Equation (9) with ${\left(RRY\right)}^{3333}$
0	0.3333	0.3366	0.3337	0.3334
1	0.3333	0.3300	0.3330	0.3333
2	0.6667	0.6667	0.6667	0.6667
3	0.3333	0.3367	0.3337	0.3334
4	0.3333	0.3299	0.3330	0.3333
5	0.6667	0.6667	0.6667	0.6667
6	0.3333	0.3368	0.3337	0.3334
7	0.3333	0.3298	0.3330	0.3333

(iii) The computation of ${\hat{B}}_{m,m^{\prime }}\left(i,{\left(RRY\right)}^n\right)$ (Equation (8) with $m=m^{\prime }=R$ and $\left|m{m}^{\prime }\right|=2$) in a simulated sequence ${\left(RRY\right)}^n$ of trinucleotide length $n=33$ (Fig. A1(B)) strongly differs from the exact probabilities (Table A1 and Fig. A1(A)).

(iv) As expected, the computation of ${\widehat{B^{\prime }}}_{m,m^{\prime }}\left(i,{\left(RRY\right)}^n\right)$ (Equation (9) with $m=m^{\prime }=R$ and $\left|m{m}^{\prime }\right|=2$) of ${\left(RRY\right)}^n$ leads to values close to the exact probabilities with a simulated sequence of short length ($n=33$ trinucleotides) and to the exact probabilities with a simulated sequence of large length ($n=3333$ trinucleotides) (Table A1).

Figure A1.

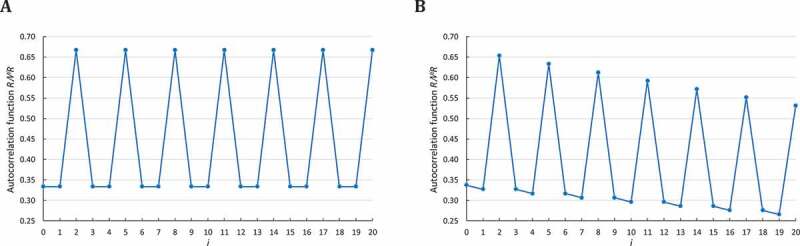
Correlation function $A_{R,R}\left(i,{\left(RRY\right)}^n\right)$ in a simulated sequence ${\left(RRY\right)}^n$. The abscissa represents the number $i$ of letters $N$ between $R$ and itself (i.e. $R$ and $R$), $i$ varying from 0 to $imax=20$. The ordinate gives the occurrence probability $A_{R,R}\left(i,{\left(RRY\right)}^n\right)$ of $R{N}^{i}R$ in ${\left(RRY\right)}^n$ computed according to A: $A_{R,R}\left(i,{\left(RRY\right)}^{33}\right)$ (Equation (3)) and B: ${\hat{B}}_{R,R^{\prime }}\left(i,{\left(RRY\right)}^{33}\right)$ (Equation (8)) .

In summary, only Equation (3) allows to compute exact probabilities with a sequence of a short length, i.e. about 100 nucleotides which is the length of a tRNA for example.

• (2) Sequence $\mathit{w}={\left(RNY\right)}^{+}$

In this second example, we show that even Equation (3) is not enough to retrieve exact probabilities in a noisy sequence of short length. However, Equation (5) extending Equation (3) to a sequence population, retrieves the exact probabilities. We will apply the correlation function $A_{R,R}\left(i,w\right)$ on the sequence $w={\left(RNY\right)}^{+}=RNYRNY\dots$, $N$ being randomly chosen between $R$ and $Y$ with equiprobability ($1/2$) for sake of simplicity, in order to introduce (basic) noise and evaluate the behaviour of the computed correlation functions.

Figure A2.

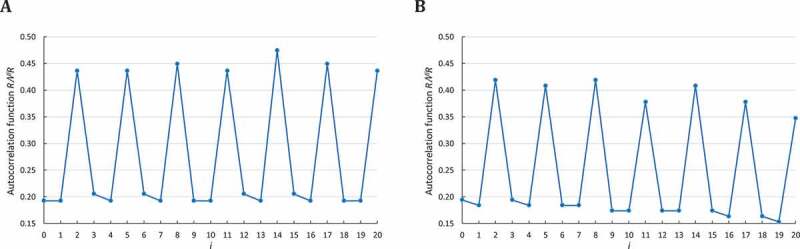
Correlation function $A_{R,R}\left(i,{\left(RNY\right)}^n\right)$ in a simulated sequence ${\left(RNY\right)}^n$. The abscissa represents the number $i$ of letters $N$ between $R$ and itself, $i$ varying from 0 to $imax=20$. The ordinate gives the occurrence probability $A_{R,R}\left(i,{\left(RNY\right)}^n\right)$ of $R{N}^{i}R$ in ${\left(RNY\right)}^n$ computed according to A: $A_{R,R}\left(i,{\left(RNY\right)}^{33}\right)$ (Equation (3)) and B: ${\hat{B}}_{R,R^{\prime }}\left(i,{\left(RNY\right)}^{33}\right)$ (Equation (8)) .

(i) Exact calculus of ${\mathrm{A}}_{\mathrm{R},\mathrm{R}}\left(\mathrm{i},{\left(\mathrm{R}\mathrm{N}\mathrm{Y}\right)}^{+}\right)$ leads trivially to the following solution

$${\mathrm{A}}_{\mathrm{R},\mathrm{R}}\left(\mathrm{i},{\left(\mathrm{R}\mathrm{N}\mathrm{Y}\right)}^{+}\right)=\left\{\begin{array}{c}\frac{1}{6}\approx 0.1667\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{i}\equiv 0\left(\mathrm{m}\mathrm{o}\mathrm{d}3\right)\\ \frac{1}{6}\approx 0.1667fori\equiv 1\left(mod3\right)\\ \frac{5}{12}\approx 0.4167fori\equiv 2\left(mod3\right)\end{array}\right..$$

(ii) The computation of $A_{R,R}\left(i,{\left(RNY\right)}^n\right)$ (Equation (3)) in a simulated sequence of $n=33$ consecutive trinucleotides $RNY$ is close to the exact probabilities (Fig. A2(A)).

Figure A3.

Correlation function $A_{R,R}\left(i,{\left(RNY\right)}_F^n\right)$ in simulated sequences ${\left(RNY\right)}_{100}^{33}$ with $\left|F\right|=100$ sequences of $n=33$ consecutive trinucleotides $RNY$. The abscissa represents the number $i$ of letters $N$ between $R$ and itself, $i$ varying from 0 to $imax=20$. The ordinate gives the occurrence probability $A_{R,R}\left(i,{\left(RNY\right)}_F^n\right)$ of $R{N}^{i}R$ in ${\left(RNY\right)}_F^n$ according to A: $A_{R,R}\left(i,{\left(RNY\right)}_{100}^{33}\right)$ (Equation (5)) and B: ${\hat{B}}_{R,R^{\prime }}\left(i,{\left(RNY\right)}_{100}^{33}\right)$ (Equation (10)) .

(iii) The computation of ${\hat{B}}_{m,m^{\prime }}\left(i,{\left(RNY\right)}^{33}\right)$ (Equation (8) with $m=m^{\prime }=R$ and $\left|m{m}^{\prime }\right|=2$) in a simulated sequence ${\left(RNY\right)}^n$ of trinucleotide length $n=33$ (Fig. A2(B)) again differs from the exact probabilities.

We continue the example by showing the importance of a sequence population when the sequences of short lengths are noisy. As an illustration example, we chose a population with $\left|F\right|=100$ sequences of $n=33$ consecutive trinucleotides $RNY$, noted ${\left(RNY\right)}_F^n={\left(RNY\right)}_{100}^{33}$.

(iii) The computation of $A_{R,R}\left(i,{\left(RNY\right)}_F^n\right)$ (Equation (5)) in simulated sequences ${\left(RNY\right)}_{100}^{33}$ retrieves the exact probabilities (Figure A3(A)).

(iv) The computation of ${\hat{B}}_{m,m^{\prime }}\left(i,{\left(RNY\right)}_F^n\right)$ (Equation (10) with $m=m^{\prime }=R$ and $\left|m{m}^{\prime }\right|=2$) in simulated sequences ${\left(RNY\right)}_{100}^{33}$ (Fig. A3(B)) again differs from the exact probabilities significantly.

In conclusion, the correlation method developed in Section Materials and methods allows to retrieve exact probabilities with noisy sequences of short lengths, and thus is well adapted to study rRNAs and tRNAs.

Appendix B

Table B1.

Bacterial organisms used in the ribosomal RNA multiple sequence alignments.

Actinoplanes utahensis	Myxococcus xanthus
Aeromonas ichthiosmia	Neisseria meningitidis
Agrobacterium tumefaciens	Nitrospira moscoviensis
Aquifex aeolicus	Paracoccus denitrificans
Bacillus cereus	Pelobacter acetylenicus
Bacillus globisporus	Pirellula marina
Bacillus halodurans.	Piscirickettsia salmonis
Bacillus licheniformis	Polynucleobacter necessarius
Bacteroides fragilis	Propionigenium modestum
Bartonella quintana	Proteus vulgaris
Bifidobacterium bifidum	Pseudomonas aeruginosa
Brevundimonas diminuta	Pseudomonas fluorescens
Buchnera aphidicola	Psychrobacter pacificensis
Caedibacter caryophila	Rahnella aquatilis
Caloramator indicus	Rhizobium sp.
Chlorobium vibrioforme	Rhizobium tropici
Chlorogloeopsis sp	Rhodopseudomonas palustris
Clavibacter xyli	Rhodospirillum rubrum
clone CS981 (X81184)	Rhodothermus marinus
clone SAR (U34043)	Rice yellow dwarf phytoplasma
Clostridium ghoni	Rubrobacter radiotolerans
Clostridium hastiforme	Ruminobacter amylophilus
Clostridium sphenoides	Saccharococcus thermophilus
Coprothermobacter proteolyticus	Salinicoccus roseus
Deferribacter thermophilus	Sargasso Sea (X52169)
Desulfacinum infernum	Serratia marcescens
Desulfitobacterium frappieri	Shewanella algae
Desulfofustis glycolicus	Simkania negevensis
Desulfohalobium retbaense	Sinorhizobium meliloti
Desulfotalea psychrophila	Spirochaeta sp.
Desulfotomaculum thermosapovorans	Spirulina platensis
Desulfurella acetivorans	Sporobacter termitidis
Dichelobacter nodosus	Staphylococcus condimenti
endosymbiont of L29265	Streptococcus macedonicus.
epibiont of L35522	Streptococcus pyogenes
Escherichia coli	Streptomyces acidiscabies
Frankia sp.	Streptomyces sampsonii
Geotoga subterranea	Sulfobacillus thermosulfidooxidans
Glycaspis brimblecombei (AF263561)	symbiont S (M27040)
Haloanaerobium lacuroseus	Synechocystis PCC6803
Halomonas sp. NIBH P1H25	Syntrophus buswellii
Helicobacter pylori	Thermomonospora chromogena
Kineococcus like bacterium AS2960	Thermotoga maritima
Lactobacillus acidophilus	uncultured bacterium (AY212656)
Lactococcus lactis	uncultured Pseudomonas sp (DQ234150)
Lactosphaera pasteurii	Ureaplasma urealyticum
Legionella lytica	Vibrio vulnificus
Magnetobacterium bavaricum	Xylella fastidiosa
Mesorhizobium loti	Zoogloea ramigera
Moraxella lacunata	Zoogloea ramigera
Mycobacterium leprae	Zymomonas mobilis
Mycoplasma capricolum

Table B2.

Bacterial tRNA sequences used in the analysis.

Amino acid	No. of sequences	Amino acid	No. of sequences	Amino acid	No. of sequences
Ala	361	Gly	406	Pro	317
Arg	329	His	158	Ser	707
Asn	197	Ile	204	Thr	427
Asp	181	Leu	688	Trp	163
Cys	150	Lys	260	Tyr	172
Gln	229	Met	511	Val	337
Glu	237	Phe	173

Disclosure statement

No potential conflict of interest was reported by the authors.