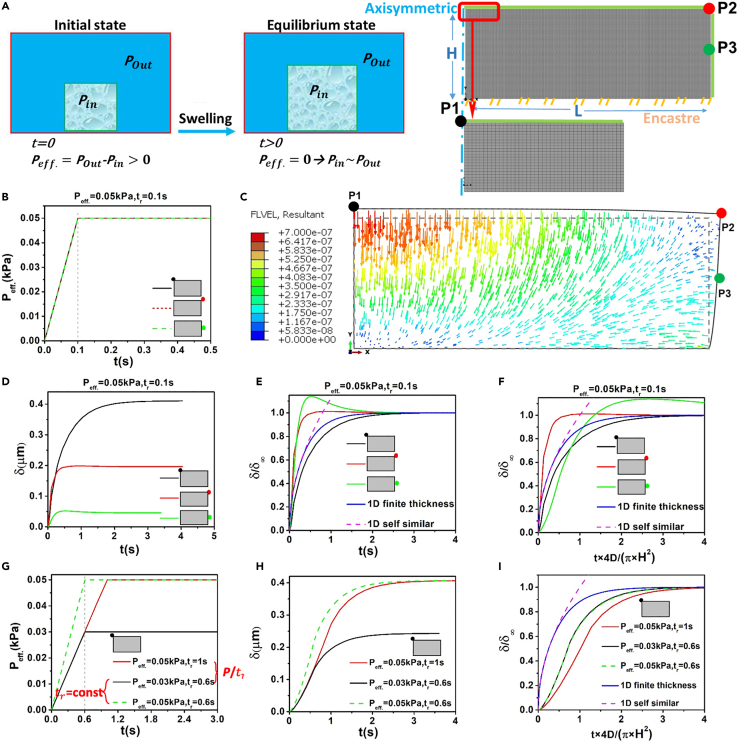
Figure 3.

Effects of spatial location, rise time, effective pressure for constrained swelling of a simple geometry investigated by FE linear poroelastic simulations

(A) Idealised swelling of a thin layer of a poroelastic material attached from one side to a substrate and initially at equilibrium $P_{eff.}$.∼ P_out- P_in= 0. Axisymmetric FE model of a thin disk with thickness H and length L was built to simulate effective pressure-driven swelling considering $P_{eff.}$ > 0 → P_in < P_out. Vertical displacements of specific nodes located at different positions P1, P2, and P3 were studied.

(B) Linear increase of effective pressure from 0 to $P_{eff.}$ = 0.05 kPa over a rise time t_r = 0.1s.

(C) The swelling type deformation of the hydrogel due to application of pressure difference and inflowing of water. Dash and solid lines indicate non-deformed and deformed material boundaries respectively. The fluid velocity field is distributed non-uniformly at boundaries and within the domain and induces a non-uniform swelling behavior across the geometry.

(D) Plot of vertical $\delta$ over time considering the ramp in pressure indicated in (B).

(E) Normalization of (D) considering $\frac{{\delta }_{}}{{\delta }_{\infty }}$ for y axis and plots of 1D finite thickness and self-similar solutions.

(F) Normalization of (D) considering $\tau =\frac{4Dt}{\pi H^2}$ for x axis and $\frac{{\delta }_{}}{{\delta }_{\infty }}$ for y axis.

(G) Application of ramp with two different $P_{eff.}$ and two different $t_r$.

(H) Considering conditions in (G), the plots of vertical displacement $\delta$ vs time were extracted for position P1.

(I) Normalization of both x and y axis led to the overlaying of the curves when ${\left(\frac{P_{eff.}}{{{\delta }_{\infty }}_{}}\right)}_1={\left(\frac{P_{eff.}}{{\delta }_{\infty }}\right)}_2.$ The analytical solutions cannot fit any of the normalized curves.