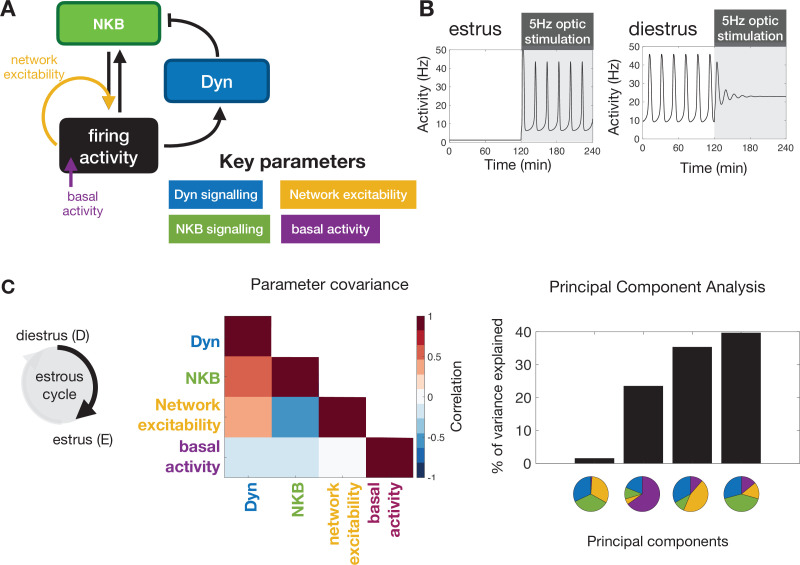
Figure 3. Model predictions on the key mechanisms modulating the behaviour of the KNDy pulse generator across the ovarian cycle.

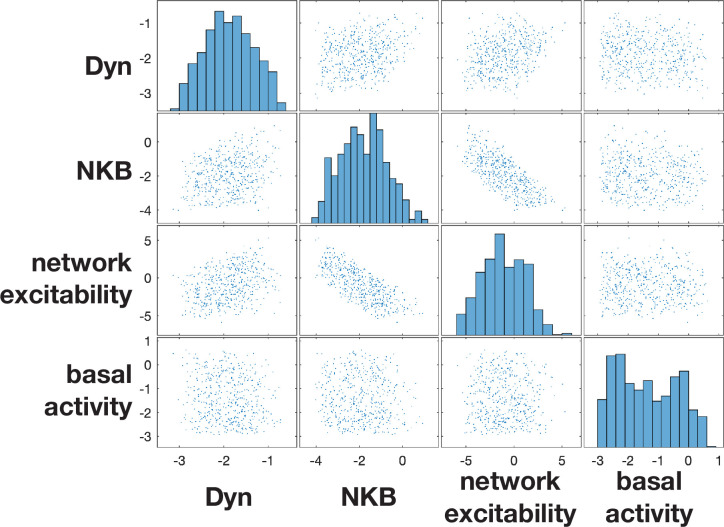
(A) Schematic illustration of the coarse-grained model of the ARC KNDy population. The model comprises three dynamical variables representing the average levels of Dyn and NKB secreted by the population, and its average firing activity. We hypothesise that four key parameters modulate the behaviour of the system across the ovarian cycle: (i) Dyn signalling strength; (ii) NKB signalling strength; (iii) network excitability; and (iv) basal neuronal activity. Estimates for the four parameters in estrus and diestrus are inferred from LH pulse frequency data in estrus and diestrus animals; with or without 5 Hz optic stimulation (Figure 2E&F) (B) System response to low frequency stimulation during estrus and diestrus, using the maximum a-posteriori estimate of the parameter values inferred from the frequency data. (C) Analysis of parameter changes across the cycle. For each of the four parameter ${\displaystyle \left({\theta }^i;i=1,2,3,4\right)}$, the diestrus-to-estrus change is defined as the log-ratio between the corresponding parameter values, that is, ${\displaystyle lo{g}_{10}\left({\theta }_{estrus}^i/{\theta }_{diestrus}^i\right).}$ Normalised covariance (correlation) matrix of parameter changes reveals negative correlation between changes in NKB signalling strength and network excitability, and positive correlation between Dyn signalling strength and both NKB signalling. Eigen-parameters are visualised as pie charts. The eigen-parameter explaining the least of the variance in the posterior distribution corresponds to the stiffest parameter combination to which the system is most sensitive.

Figure 3—figure supplement 1. Posterior distributions of diestrus-to-estrus parameter changes inferred from data.

The behaviour of the model depends upon four parameters: (i) Dyn signalling strength; (ii) NKB signalling strength; (iii) network excitability and (iv) basal neuronal activity. For each of the four parameter (${\theta }^i;i=\mathrm{1,2},\mathrm{3,4}$), we quantify the diestrus-to-estrus change as the log-ratio between the corresponding parameters, that is, ${log}_{10}\frac{{\theta }_{estrus}^i}{{\theta }_{diestrus}^i}$, and we infer them from frequency of LH pulses using Approximate Bayesian Computation based on sequential Monte Carlo (see main text).