Figure 1.

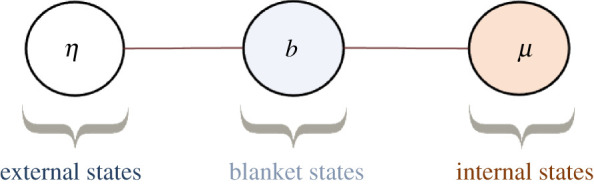
Markov blanket depicted graphically as an undirected graphical model, also known as a Markov random field [4,31]. (A Markov random field is a Bayesian network whose directed arrows are replaced by undirected arrows.) The circles represent random variables. The lines represent conditional dependencies between random variables. The Markov blanket condition means that there is no line between $\mu$ and $\eta$. This means that $\mu$ and $\eta$ are conditionally independent given $b$. In other words, knowing the internal state $\mu$, does not afford additional information about the external state $\eta$ when the blanket state $b$ is known. Thus blanket states act as an informational boundary between internal and external states. (Online version in colour.)