Drosophila Evolution over Space and Time (DEST): A New Population Genomics Resource

Abstract

Drosophila melanogaster is a leading model in population genetics and genomics, and a growing number of whole-genome data sets from natural populations of this species have been published over the last years. A major challenge is the integration of disparate data sets, often generated using different sequencing technologies and bioinformatic pipelines, which hampers our ability to address questions about the evolution of this species. Here we address these issues by developing a bioinformatics pipeline that maps pooled sequencing (Pool-Seq) reads from D. melanogaster to a hologenome consisting of fly and symbiont genomes and estimates allele frequencies using either a heuristic (PoolSNP) or a probabilistic variant caller (SNAPE-pooled). We use this pipeline to generate the largest data repository of genomic data available for D. melanogaster to date, encompassing 271 previously published and unpublished population samples from over 100 locations in >20 countries on four continents. Several of these locations have been sampled at different seasons across multiple years. This data set, which we call Drosophila Evolution over Space and Time (DEST), is coupled with sampling and environmental metadata. A web-based genome browser and web portal provide easy access to the SNP data set. We further provide guidelines on how to use Pool-Seq data for model-based demographic inference. Our aim is to provide this scalable platform as a community resource which can be easily extended via future efforts for an even more extensive cosmopolitan data set. Our resource will enable population geneticists to analyze spatiotemporal genetic patterns and evolutionary dynamics of D. melanogaster populations in unprecedented detail.

Introduction

The vinegar fly Drosophila melanogaster is one of the oldest and most important genetic model systems and has played a key role in the development of theoretical and empirical population genetics (e.g., Schneider 2000; Hales et al. 2015; Haudry et al. 2020). Through decades of work, we now have a basic picture of the evolutionary origin (David and Capy 1988; Lachaise et al. 1988; Keller 2007; Sprengelmeyer et al. 2020), colonization history and demography (Caracristi and Schlötterer 2003; Li and Stephan 2006; Duchen et al. 2013; Grenier et al. 2015; Bergland et al. 2016; Arguello et al. 2019; Kapopoulou et al. 2020), and spatiotemporal diversification patterns of this species and its close relatives (Kolaczkowski et al. 2011; Fabian et al. 2012; Bergland et al. 2014; Kapun et al. 2016, 2020; Lack et al. 2016; Machado et al. 2016, 2021). The availability of high-quality reference genomes (Adams 2000; Celniker and Rubin 2003; dos Santos et al. 2015) and genetic tools (Schneider 2000; Duffy 2002; Jennings 2011; Hales et al. 2015; Haudry et al. 2020) facilitates placing evolutionary studies of flies in a mechanistic context, allowing for the functional characterization of ecologically relevant polymorphisms (e.g., de Jong and Bochdanovits 2003; Paaby et al. 2010, 2014; Mateo et al. 2014; Kapun et al. 2016; Durmaz et al. 2018, 2019; Ramaekers et al. 2019).

Recently, work on the evolutionary biology of Drosophila has been fueled by a growing number of population genomic data sets from field collections across a large portion of D. melanogaster's range (Kapun et al. 2020; Grenier et al. 2015; Arguello et al. 2019; Guirao-Rico and González 2019; Machado et al. 2021). These genomic data consist either of re-sequenced inbred (or haploid) individuals (e.g., Langley et al. 2012; Mackay et al. 2012; Grenier et al. 2015; Lack et al. 2015, 2016; Mateo et al. 2018; Kapopoulou et al. 2020) or pooled sequencing (Pool-Seq) of outbred population samples (Pool-Seq; e.g., Kolaczkowski et al. 2011; Fabian et al. 2012; Bastide et al. 2013; Campo et al. 2013; Bergland et al. 2014; Machado et al. 2016, 2021; Kapun et al. 2016, 2020). Pooled resequencing provides accurate and precise estimates of allele frequencies across most of the allele frequency spectrum (Zhu et al. 2012; Lynch et al. 2014; Schlötterer et al. 2014) at a fraction of the cost of individual-based sequencing. Although Pool-Seq retains limited information about linkage disequilibrium (LD) relative to individual sequencing (Feder et al. 2012), Pool-Seq data can be used to infer complex demographic histories (e.g., Cheng et al. 2012; Bergland et al. 2016; Deitz et al. 2016; Corbett-Detig and Nielsen 2017; Gould et al. 2017; Giesen et al. 2020), characterize levels of diversity (Kofler, Orozco-terWengel, et al. 2011; Kofler, Pandey, et al. 2011), and infer genomic loci involved in recent adaptation in nature (Flatt 2016; Kapun et al. 2016, 2020; Gould et al. 2017; Bogaerts‐Márquez et al. 2021; Machado et al. 2021) and during experimental evolution (e.g., Turner et al. 2011; Burke 2012; Orozco-terWengel et al. 2012; Kofler and Schlötterer 2014). However, the rapidly increasing number of genomic data sets processed with different bioinformatic pipelines makes it difficult to compare results across studies and to jointly analyze multiple data sets. Differences among bioinformatic pipelines include filtering methods for the raw reads, mapping algorithms, the choice of the reference genome, or SNP calling approaches, potentially generating biases when combining processed data sets from different sources for joint analyses (e.g., Gautier et al. 2013; Hoban et al. 2016).

To address these issues, we have developed a modular bioinformatics pipeline to map Pool-Seq reads to a hologenome consisting of fly and microbial genomes, to remove reads from potential Drosophila simulans contaminants, and to estimate allele frequencies using two complementary SNP callers. Our pipeline is available as a Docker image (available from https://dest.bio, last accessed September 6, 2021) to standardize versions of software used for filtering and mapping, to make the pipeline available independently of the operating system used, and to facilitate future updates and modification of the pipeline. In addition, our pipeline allows using either heuristic or probabilistic methods for SNP calling, based on PoolSNP (Kapun et al. 2020) and SNAPE-pooled (Raineri et al. 2012), respectively. We also provide tools for performing in silico pooling of existing inbred (haploid) lines that exist as part of other Drosophila population genomic resources (Langley et al. 2012; Pool et al. 2012; Grenier et al. 2015; Kao et al. 2015; Lack et al. 2015, 2016). This pipeline is also designed to be flexible, facilitating the streamlined addition of new population samples as they arise.

Using this pipeline, we generated a unified data set of pooled allele frequency estimates of D. melanogaster sampled across a large portion of its world-wide distribution, including Europe, North America, Africa, Australia, and Asia. This data set is the result of the collaborative efforts of the European DrosEU (Kapun et al. 2020) and DrosRTEC (Machado et al. 2021) consortia and combines both novel and previously published population genomic data. Our data set combines samples from 100 localities, 55 of which were sampled at two or more time points across the reproductive season (∼10–15 generations/year) for one or more years. Collectively, these samples represent >13,000 individuals, cumulatively sequenced to >16,000× coverage or ∼1× per fly. The cost effectiveness of Pool-Seq has enabled us to estimate genome-wide allele frequencies over geographic space (continental and subcontinental) and time (seasonal, annual, and decadal) scales, thus making our data a unique resource for advancing our understanding of fundamental adaptive and neutral evolutionary processes. We provide data in two file formats (VCF and GDS: Danecek et al. 2011; Zheng et al. 2017), thus allowing researchers to utilize a variety of tools for computational analyses. Our data set also contains sampling and environmental metadata to enable various downstream analyses of biological interest. We further employed demographic modeling to investigate the evolutionary history of two distinct genetic clusters in Europe using the Drosophila Evolution over Space and Time (DEST) Pool-Seq data set and developed guidelines for using Pool-Seq data for model-based demographic inference using the python package moments.

Results

Integrating a Worldwide Collection of D. melanogaster Population Genomics Resources

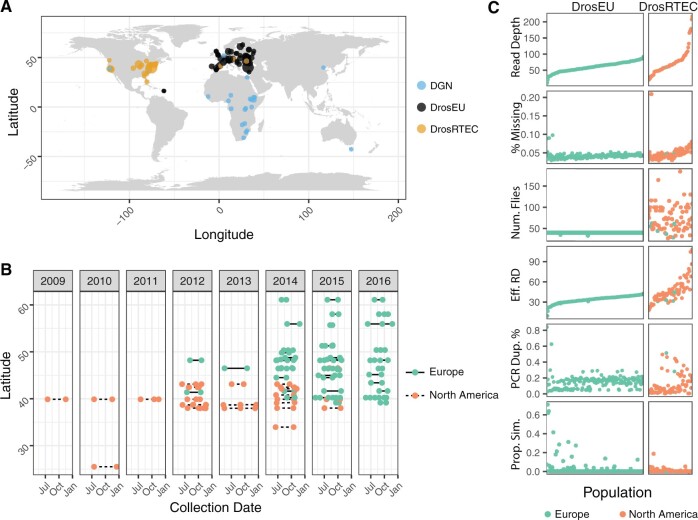
We developed a modular and standardized pipeline for generating allele frequency estimates from pooled resequencing of D. melanogaster genomes (supplementary fig. S1, Supplementary Material online). Using this pipeline, we assembled a data set of allele frequencies from 271 D. melanogaster populations sampled around the world (fig. 1A and supplementary table S1, Supplementary Material online). Many of these samples were collected at the same location, at different seasons and over multiple years (fig. 1B). The nature of the genomic data for each population varies as a consequence of biological origin (e.g., inbred lines or Pool-Seq), library preparation method, and sequencing platform.

Fig. 1.

Sampling location, dates, and quality metrics. (A) Map showing the 271 sampling localities forming the DEST data set. Colors denote the data sets of origin (DGN, DrosEU, or DrosRTEC). (B) Collection dates for localities sampled more than once. (C) General sample features of the DEST data set. The x-axis represents the population sample, ordered by the average read depth.

To assess whether these features affect basic attributes of the data set, we calculated six basic quality metrics focusing on the Pool-Seq samples (fig. 1C and supplementary table S2, Supplementary Material online). On average, median read depth across samples is 62x (range: 10–217x). The per-nucleotide missing allele frequency rate was less than 7% for most (95%) of the samples. Excluding populations with high missing data rate (>7%), the proportion of sites with missing data was positively correlated with read depth (P = 1.2 × 10⁹, R² = 0.4). The positive correlation between read depth and missing data rate is primarily due to an increased sensitivity to identify indels. The number of flies per sample varied from 33 to 205, with considerable heterogeneity among the DrosRTEC samples [standard deviation (SD) = 30], but not among DrosEU samples (SD = 0.04). Variation in the number of flies and in sequencing depth is reflected in the effective coverage (N_Eff) of each pool, an estimate of the number of independent reads after accounting for double binomial sampling that occurs during Pool-Seq (Kolaczkowski et al. 2011; Feder et al. 2012; fig. 1C). There was considerable variation in PCR duplicate rate among samples, with notable differences between batches of DrosEU samples (∼6% in 2014 vs. 18% in 2015/16; t-test, P = 1.8 × 10⁻¹⁹) and DrosRTEC samples (∼3% in samples collected as part of Bergland et al. 2014 vs. ∼14% in samples collected as part of Machado et al. 2021; P = 6.37 × 10⁻³). Curiously, the 2015/2016 DrosEU samples were made with a PCR-free kit, suggesting that the observed PCR duplicates were optical duplicates and not amplification artifacts. Contamination of samples by D. simulans varied among populations but was generally absent (<1% D. simulans specific reads; supplementary table S1, Supplementary Material online).

Identification and Quality Control of SNP Polymorphisms

In order to determine appropriate SNP calling and filtering parameters, and to identify potentially problematic population samples, we first calculated the ratio of the number of nonsynonymous polymorphisms to the number of synonymous polymorphisms (p_N/p_S) for each population sample across the whole genome. Because nonsynonymous changes are expected to be under strong purifying selection (Kreitman 1983), the p_N/p_S metric can reflect the presence of sequencing errors that would disproportionately inflate p_N relative to p_S. Our primary goal was not to provide novel estimates of p_N/p_Sbut rather to ensure that all population samples have estimates that are consistent with estimates generated from independent Drosophila data sets (Mackay et al. 2012).

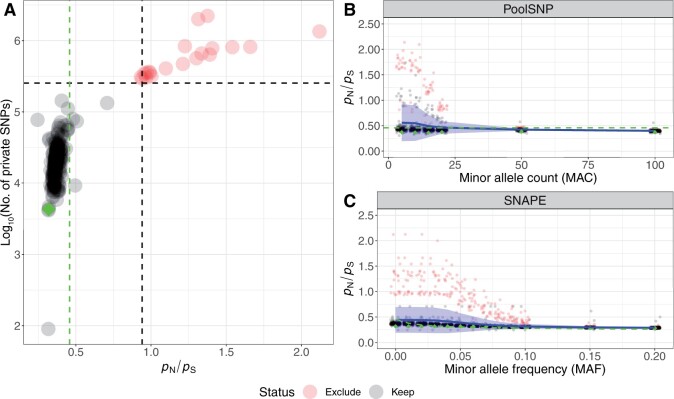
For the PoolSNP data set, we varied the global minor allele count (MAC) and global minor allele frequency (MAF) and then calculated p_N/p_S. MAC thresholds <50 resulted in large variances of p_N/p_S caused by 20 outlier populations characterized by unusually high p_N/p_S ratios and numbers of private SNPs (supplementary table S3, Supplementary Material online, and fig. 2A and B) indicating that there may be elevated numbers of sequencing errors in some samples. Some (n = 17) of these samples had previously been found to show positive values of Tajima’s D across the whole genome (Kapun et al. 2020). We observed that, as expected, p_N/p_S was negatively correlated with MAC (linear regression; P < 0.001; fig. 2B) and that applying a MAC threshold of 50 reduced the elevated p_N/p_S ratios of the 20 aforementioned outlier samples to values similar to the rest of the data set, suggesting that potential sequencing errors had been largely removed. To minimize false-positive variant calling, we chose MAC = 50 and MAF = 0.001 as conservative threshold parameters for SNP calling with PoolSNP. Using these parameters, PoolSNP identified 4,381,144 polymorphisms segregating among the 271 D. melanogaster samples (Pool-Seq plus DGN), and 4,042,456 polymorphisms segregating among the 246 Pool-Seq samples (excluding DGN).

Fig. 2.

Quality control of SNPs called with SNAPE-pooled and PoolSNP. Panel (A) shows genome-wide p_N/p_S ratios and the log10-scaled number of private SNPs for all Pool-Seq samples based on SNP calling with SNAPE-pooled. We highlight 20 outlier samples in red, which are characterized by exceptionally high values of both metrics. The dashed black lines indicate the 95% confidence limits (average + 1.96 SD) for both statistics. The vertical green dashed line highlights the empirical estimate of p_N/p_S calculated from individual sequencing data of the DGRP freeze2 data set (Mackay et al. 2012). The green diamond shows the corresponding value of the DGRP population, which was pool-sequenced as part of the DrosRTEC data set (NC_ra_03_n; Zhu et al. 2012). Panels (B) and (C) show the effects of heuristic MAC and MAF thresholds on p_N/p_S ratios in SNP data based on PoolSNP and SNAPE-pooled, respectively. Blue lines in both panels show average genome-wide p_N/p_S ratios across 271 and 246 populations, respectively. The blue ribbons depict the corresponding standard deviations. The 20 outlier samples, which are characterized in panel (A), are highlighted red. In addition, p_N/p_S ratios of the DGRP Pool-Seq sample (NC_ra_03_n) are shown at different cut-offs as green diamonds and the empirical values from the DGRP freeze2 data set are indicated as dashed green lines.

In contrast to PoolSNP, SNAPE-pooled calls variants in each sample separately using a probabilistic approach which integrates allelic information across all populations for heuristic SNP calling. To quantify the number of putative sequencing errors among low frequency variants we varied the local MAF threshold per sample and calculated p_N/p_S for each sample in the SNAPE-pooled data set. Similar to PoolSNP, we found that elevated p_N/p_S was negatively correlated with a local MAF threshold (linear regression; P < 0.001; fig. 2C) and that the 20 aforementioned problematic samples also had a strong effect on the variance and mean of p_N/p_S ratios. Accordingly, we excluded these 20 samples from further analyses of low-frequency variants and private SNPs and applied a conservative local MAF filter of 5% for the remainder of the SNAPE-pooled analysis to avoid misclassification of sequencing errors as low-frequency variants. Our SNAPE-pooled results identified 8,541,651 polymorphisms segregating among the remaining 226 samples. Below, we discuss the geographic distribution and global frequency of SNPs identified using these two methods in order to provide insight into the marked discrepancy in the number of SNPs that they identify.

Similarity of SNP Polymorphisms Detected with PoolSNP and SNAPE-Pooled

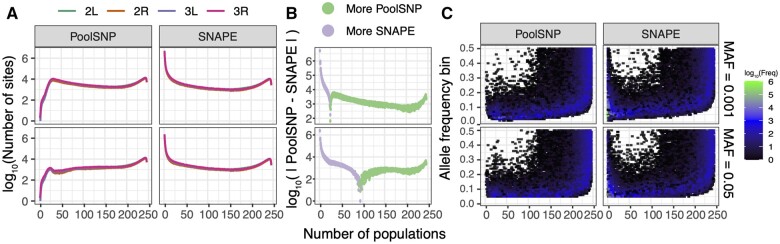
We calculated three metrics related to the amount of polymorphism discovered by our pipelines: the abundance of polymorphisms segregating in n populations across each chromosome (fig. 3A), the difference of discovered polymorphisms between SNAPE-pooled and PoolSNP (defined as the absolute value of PoolSNP minus SNAPE-pooled; fig. 3B), and the amount of polymorphism discovered per MAF bin (fig. 3C). We evaluated these three metrics across a 2 × 2 filtering scheme: two MAF filters (0.001, 0.05) and two sample sets (the whole data set of 246 samples; and the 226 samples that passed the sequencing error filter in SNAPE-pooled; see Identification and Quality Control). Notably, PoolSNP was biased toward identification of common SNPs present in multiple samples, whereas SNAPE-pooled was more sensitive to the identification of polymorphisms that appeared in few populations only (fig. 3B). For example, at a MAF filter of 0.001, SNAPE-pooled discovered more polymorphisms that were shared in less than 25 populations (relative to PoolSNP), and these accounted for ∼79% of all polymorphisms discovered by the pipeline. Likewise, at a MAF filter of 0.05, SNAPE-pooled discovered more polymorphisms that were shared in less than 97 populations; these accounted for ∼71% of all discovered polymorphisms. SNAPE-pooled identifies fewer polymorphic sites that are shared among a large number of populations than PoolSNP does because SNAPE-pooled does not integrate information across multiple populations. Consequently, SNAPE-pooled can fail to identify SNPs that are at low overall frequencies and get called as monomorphic or missing in a subset of populations given the posterior probability thresholds that we employed (see Materials and Methods).

Fig. 3.

Polymorphism data in the PoolSNP and SNAPE data sets. (A) Number of polymorphic sites discovered across populations. The x-axis shows the number of populations that share a polymorphic site. The y-axis corresponds to the number of polymorphic sites shared by any number of populations, on a log10 scale. The colored lines represent different chromosomes and are stacked on top of each other. (B) The difference of discovered polymorphisms between SNAPE-pooled and PoolSNP. (C) Number of polymorphic sites as a function of allele frequency and the number of populations in which the polymorphisms are present. The color gradient represents the number of variant alleles from low to high (black to green). The x-axis is the same as in (A), and the y-axis is the MAF. The 2 × 2 filtering scheme is shown on the right side of the figure.

We also compared AF estimates between the two callers using the data set of 226 populations applying a local MAF filter of 0.05 in the SNAPE-pooled data set (see supplementary table S2, Supplementary Material online). Among the positions identified as polymorphic by both calling methods, our frequency estimates were identical for the great majority of SNPs (92–99.67%) in all samples analyzed. Between 0.1% and 7.1% of the polymorphic SNPs differed by less than 5% frequency between the two methods, 0.003–2.1% of polymorphic SNPs differed by 5–10% frequency and only up to 0.3% varied >10% frequency (supplementary table S4, Supplementary Material online). Finally, on average 13.32% of the positions analyzed were called as polymorphic by PoolSNP whereas there were monomorphic or no data according to SNAPE-pooled, consistent with the use of a hard threshold of the posterior-probability in the SNAPE calling step (supplementary table S4, Supplementary Material online).

Mutation-Class Frequencies

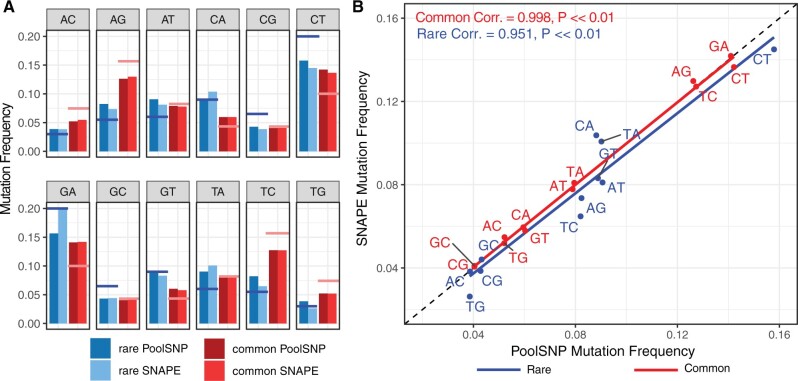
We estimated the percentage of mutation classes (e.g., A → C, A → G, A → T, etc.) accepted as polymorphisms in both our SNP calling pipelines and classified these loci as being either “rare” (i.e., AF <5% and shared in less than 50 populations) or “common” (AF >5% and shared in more than 150 populations). For this analysis, we classified the minor allele as the derived allele. Figure 4A shows the percentage of each mutation class for the 226 populations which passed filters in both SNAPE-pooled and PoolSNP. In addition, we overlaid, as a horizontal line, the expected mutation frequencies for rare (blue; Assaf et al. 2017) and common (red; Mackay et al. 2012) mutations. In general, our SNP discovery pipelines produced mutation-class relative frequencies of rare and common mutations that are consistent with empirical expectations, however, there were some exceptions to this pattern. For example, the frequencies of the C/G rare mutation-class were consistently underestimated by both callers, a phenomenon that might be related to the known GC bias of modern sequencing machines (Benjamini and Speed 2012). The correlation between SNP calling pipelines was high across both common and rare mutation classes, with marginal discrepancies observed for rare variants (fig. 4B).

Fig. 4.

Frequencies of observed nucleotide polymorphism in the DEST data set (226 populations common to PoolSNP and SNAPE-pooled). (A) Each panel represents a mutation type. The red color indicates common mutations (AF >0.05, and common in more than 150 populations) whereas the blue color indicates rare mutations (AF <0.05, and shared in less than 50 populations). The dark colors correspond to the PoolSNP pipeline and the soft colors correspond to the SNAPE-pooled pipeline. The hovering red and blue horizontal lines represent the estimated mutation rates for common and rare mutations, respectively. (B) Correlation between the observed mutation frequencies seen in SNAPE-pooled and PoolSNP. The one-to-one correspondence line is shown as a black-dashed diagonal. Correlation estimates (Pearson’s correlation) and P values for common and rare mutations are shown.

Inversion Frequencies

Using a set of inversion-specific marker SNPs (Kapun et al. 2014), we estimated the frequencies of seven cosmopolitan inversion polymorphisms (In(2L)t, In(2R)NS, In(3L)P, In(3R)C, In(3R)K, In(3R)Mo, and In(3R)Payne). We found that most of the 271 populations were polymorphic for at least one or more chromosomal inversions (supplementary table S1, Supplementary Material online). Although most inversions were either absent or rare (average frequencies: In(2R)NS = 5.2% [± 4.7% SD], In(3L)P = 3.1% [± 4.3% SD], In(3R)C = 2.5% [± 2.3% SD], In(3R)K = 1.8% [± 7.4% SD], In(3R)Mo = 2.2% [± 3.6% SD] and In(3R)Payne = 5.7% [± 7.1% SD]), only In(2L)t segregated at substantial frequencies in most populations (average frequency = 18.3% [± 11% SD]). We found that our novel inversion frequency estimates of the DrosEU data from 2014 were highly consistent with previous estimates from Kapun et al. (2020) as coefficients of determination (R²) ranged from 91% to 99%.

Comparison to Previously Published Data Sets

We compared the allele frequency and read depth estimates from the DEST data set (based on PoolSNP) to previously published estimates by Bergland et al. (2014), and Kapun et al. (2020), Machado et al. (2021). For these data sets, we employed two types of correlations: the nominal correlation (i.e., Pearson’s correlation; CO) and the concordance correlation coefficient (CCC; Lin 1989; Liao and Lewis 2000). The CCC determines how much the observed data deviate from the line of perfect concordance (i.e., the 45 degree-line on a square scatter plot).

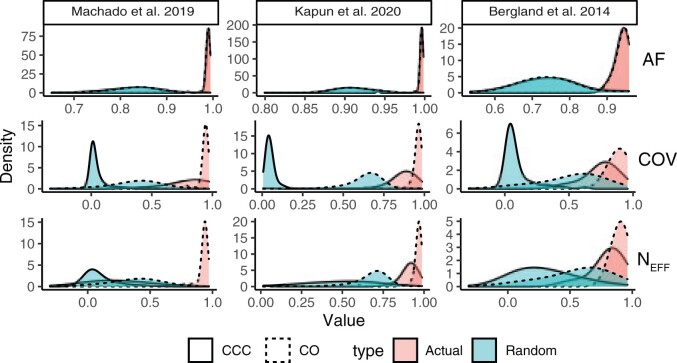
Estimates of allele frequency were strongly correlated and consistent with previously published data. The strongest correlation of DEST AF and previously published AF was observed with the data of Kapun et al. (2020) (average CO and CCC >0.99; fig. 5, top row and supplementary fig. S4, Supplementary Material online). AF correlations with Machado et al. (2021) are also generally high (average CO and CCC >0.98; fig. 5, top row and supplementary fig. S5, Supplementary Material online). AF correlations with the data from Bergland et al. (2014) were lower (0.94; supplementary fig. S6, Supplementary Material online), likely reflecting differences in data processing and quality control.

Fig. 5.

Correlations between DEST data set and previously published data sets. Correlations between allele frequencies (AF), Nominal Coverage (COV), and Effective Coverage (N_EFF) between the DEST data set (using the PoolSNP method) and the three previous Drosophila data sets: Machado et al. (2021), Kapun et al. (2020), and Bergland et al. (2014). For each data set, we show the distribution of two types of correlation coefficients: the nominal (Pearson’s) correlation (CO; dashed lines) and the concordant correlation (CCC; solid lines). In addition to the actual correlations between the data sets (red distributions), we show the distributions of correlations estimated with random population pairs (green distributions).

We also examined two aspects of read depth, that is, nominal coverage (COV), the number of reads mapping to a site that has passed quality control, and N_Eff (Kofler, Orozco-terWengel, et al. 2011; Kolaczkowski et al. 2011; Feder et al. 2012; Schlötterer et al. 2014). Similar to AF estimates, the Pearson correlation coefficients for both coverage and effective coverage were large (0.92, 0.95, 0.90 for Machado et al. [2021], Kapun et al. [2020], and Bergland et al. [2014], respectively; see supplementary figs. S7–S12, Supplementary Material online), indicating that sample identity was preserved appropriately. However, the concordance correlation coefficients were substantially lower between the data sets (0.24, 0.88, 0.79, respectively), indicating systematic differences in read depth between the DEST data set and previously published data. Indeed, read depth estimates were on average ∼12%, ∼14%, and ∼20% lower in the DEST data set as compared with the previously published data in Machado et al. (2021), Kapun et al. (2020), and Bergland et al. (2014), respectively. The lower read depth and effective read depth estimates in the DEST data set reflect our more stringent quality control and filtering.

Genetic Diversity

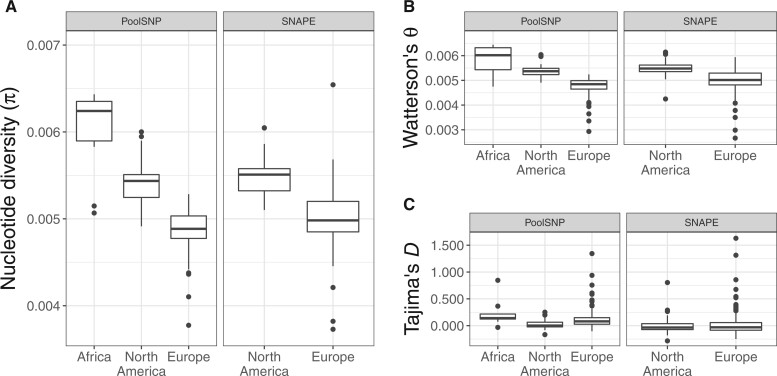
We estimated nucleotide diversity (π), Watterson’s θ, and Tajima’s D for both the PoolSNP and SNAPE-pooled data sets (supplementary table S5, Supplementary Material online). Results for the African, European, and North American population samples are presented in figure 6 (also see supplementary fig. S13, Supplementary Material online for estimates by chromosome arm). All estimates were positively correlated between PoolSNP and SNAPE-pooled (P < 0.001), with Pearson’s correlation coefficients of 0.90, 0.83, and 0.70 for π, Watterson’s θ, and Tajima’s D, respectively. Higher values of genetic diversity were obtained for the SNAPE-pooled data set, probably due to its higher sensitivity for detecting rare variants (see Patterns of Polymorphism between PoolSNP and SNAPE-Pooled). Pool size had no significant effect on the four summary statistics in European or in North American populations (linear models, all P > 0.05), suggesting that data from populations with heterogeneous pool sizes can be safely merged for accurate population genomic analysis.

Fig. 6.

Population genetic estimates for African, European, and North American populations. Shown are genome-wide estimates of (A) nucleotide diversity (π), (B) Watterson’s θ and (C) Tajima’s D for African populations using the PoolSNP data set, and for European and North American populations using both the PoolSNP and SNAPE-pooled (SNAPE) data sets. As can be seen from the figure, estimates based on PoolSNP versus SNAPE-pooled (SNAPE) are highly correlated (see main text). Genetic variability is seen to be highest for African populations, followed by North American and then European populations, as previously observed (e.g., see Lack et al. [2016] and Kapun et al. [2020]).

The highest levels of genetic diversity were observed for ancestral African populations (mean π = 0.0060, mean θ = 0.0059); North American populations exhibited higher genetic variability (mean π = 0.0054, mean θ = 0.0054) than European populations (mean π = 0.0049, mean θ = 0.0048). These results are consistent with previous observations based on individual genome sequencing (e.g., see Lack et al. [2016] and Kapun et al. [2020]). Our observations are also consistent with previous estimates based on pooled data from three North American populations (mean π = 0.00577, mean θ = 0.00597; Fabian et al. 2012) and 48 European populations (mean π = 0.0051, mean θ = 0.0052; Kapun et al. 2020). Estimates of Tajima’s D were positive when using PoolSNP, and slightly negative using SNAPE. These results are expected given biases in the detection of rare alleles between these two SNP calling methods. In addition, our estimates for π, Watterson’s θ and Tajima’s D were positively correlated with previous estimates for the 48 European populations analyzed by Kapun et al. (2020) (all P < 0.01). Notably, slightly lower levels of Tajima’s D in North America as compared with both Africa and Europe (fig. 6C) may be indicative for admixture (Stajich and Hahn 2005), which has been identified previously along the North American east coast (Caracristi and Schlötterer 2003; Kao et al. 2015; Bergland et al. 2016).

Phylogeographic Clusters in D. melanogaster

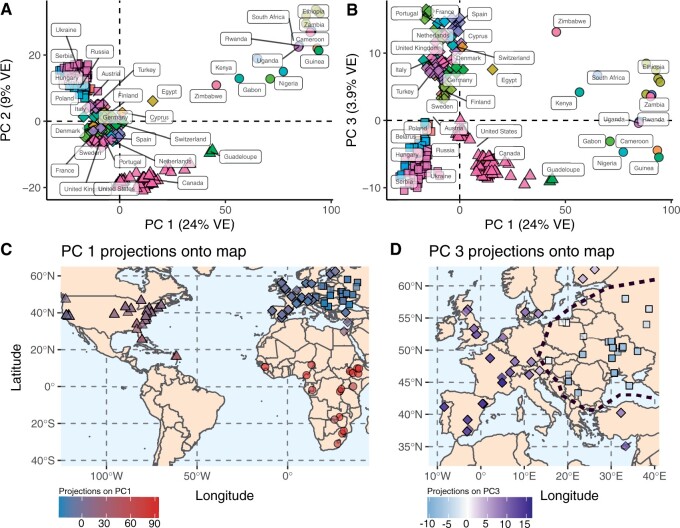
We performed PCA on the PoolSNP variants using samples from the North American (DrosRTEC), European (DrosEU), and African (DGN) data sets (excluding all Asian and Oceanian samples). Prior to analysis, we filtered the joint data sets to include only high-quality biallelic SNPs. Because LD decays rapidly in Drosophila (Comeron et al. 2012), we only considered SNPs at least 500 bp away from each other. PCA on the resulting 100,000 SNPs revealed evidence for discrete phylogeographic clusters that correspond to geographic regions (supplementary fig. S14B, Supplementary Material online). PC1 (24% variance explained [VE]) partitions samples between Africa and the other continents (fig. 7A). PC2 (9% VE) separates European from North American populations, and both PC2 and PC3 (4% VE) divide Europe into two population clusters (fig. 7B). As expected, North American samples are intermediate to European and African samples, presumably due to recent secondary contact (Kao et al. 2015; Pool 2015; Bergland et al. 2016). Notably, these spatial relationships become evident when PCA projections from each sample are plotted onto a world map (fig. 7C). Interestingly, the emergent clusters in Europe are not strictly defined by geography. For example, the western cluster (diamonds in fig. 7D) includes Western Europe as well as Finland, Turkey, Cyprus, and Egypt. The eastern cluster, on the other hand, consists of several populations collected in previous Soviet republics as well as Poland, Hungary, Serbia and Austria. Below, we use demographic modeling to resolve the split time between these clusters.

Fig. 7.

Demographic signatures of the DrosEU, DrosRTEC, and DGN data (using the PoolSNP pipeline). (A) PCA dimensions 1 and 2. The mean centroid of a country’s assignment is labeled. (B) PCA dimensions 1 and 3. (C) Projections of PC1 onto a World map. PC1 projections define the existence of continental level clusters of population structure (indicated by the shapes circles: Africa; triangles: North America; diamonds and squares: Europe). (D) Projections of PC3 onto Europe. These projections show the existence of a demographic divide within Europe: the diamond shapes indicate a western cluster, whereas the squares represent an eastern cluster. For panels (C) and (D), the intensity of the color is proportional to the PC projection. The black dashed line shows the two-cluster divide.

A unique feature of this data set is that it contains a mixture of Pool-Seq and inbred (or haploid) genome data. For some geographic regions, the DEST data set contains both data types. Inbred and Pool-Seq samples from nearby geographic regions clustered in the same regions of PC space (supplementary fig. S15, Supplementary Material online). Excluding the DGN-derived African samples, no PC was significantly correlated with data type (PC1: P = 0.352, PC2: P = 0.223, PC3: P = 0.998).

Geographic Proximity Analysis

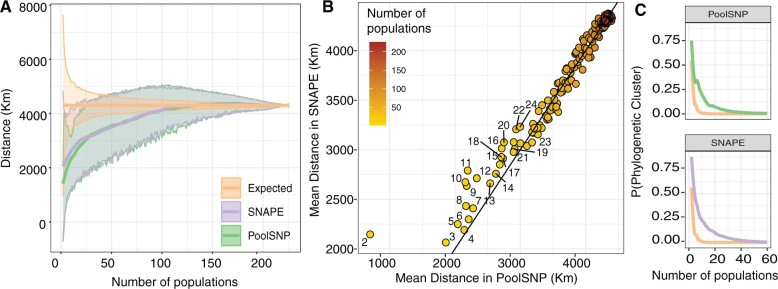
The geographic distribution of our samples allows leveraging basic principles of phylogeography and population genetics to assess the biological significance of rare SNPs (Wright 1943; Battey et al. 2020). We expect to observe young neutral alleles at low frequencies among geographically close populations, reflecting isolation by distance. We tested this hypothesis by estimating the average geographic distance among pairs of populations that share SNPs only occurring in these two populations (doubletons), among three populations that share tripletons, and so forth. Without imposing a MAF filter, both SNAPE-pooled and PoolSNP pipelines produced patterns concordant with the expectation. That is, populations in close proximity were more likely to share rare mutations relative to random chance pairings (fig. 8A). Notably, SNPs identified in less than 25 populations tend to be geographically closer in PoolSNP, relative to SNAPE-pooled. The primary source of this discrepancy between callers occurs when evaluating SNPs shared by just two populations (fig. 8B). In the case of PoolSNP, only 0.0006% of all SNPs are private to just two populations and the mean geographical distance is 702 km. In the case of SNAPE-pooled, 9.3% of all SNPs are private to two populations and the mean distance is ∼2,000 km. Aside from the case of n = 2, the difference in proximity estimates between the callers is minimal. These findings suggest that some of the SNAPE-pooled SNPs which only segregate in two populations or less might be false positives. To further evaluate these geographical patterns, we estimated the probability that any given population pair belongs to a particular phylogeographic cluster (supplementary fig. S16, Supplementary Material online) as a function of their shared variants. Our results indicate that rare variants, private to geographically proximate populations, are strong predictors of phylogeographic provenance (see fig. 8C).

Fig. 8.

Geographic proximity analysis. (A) Average (local regression; LOESS) geographic distance between populations that share a polymorphism at any given site for PoolSNP and SNAPE-pooled. The x-axis represents the number of populations considered; the y-axis is the mean geographic distance among samples. The yellow line represents the random expectation calculated as random pairings of the data. The band around the lines is the standard deviation of the estimator. (B) Correlation graph showing the different mean distance estimate for both callers as a function of the number of populations (the groups from n = 2 to n = 25 are labeled in the graph). A 1-to-1 line is also shown. (C) Probability that all populations containing a polymorphic site come from the same phylogeographic cluster (as defined by PC space, fig. 7 and supplementary fig. S14, Supplementary Material online). The y-axis is the probability of “x” populations belonging to the same phylogeographic cluster. The axis only shows up to 60 populations since, after 40 populations, the probabilities approach 0. The colors are consistent across panels.

Geographically Informative Markers

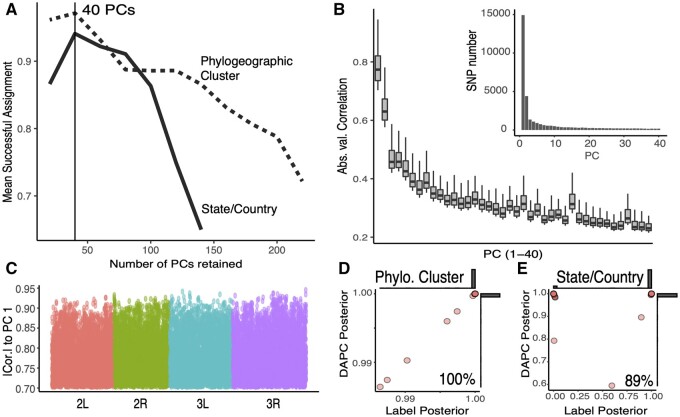
An inherent strength of our broad biogeographic sampling is the potential to generate a panel of core demography SNPs to investigate the provenance of current and future samples. We created a panel of geographically informative markers (GIMs) by conducting a discriminant analysis of principal components (DAPC) to discover which loci drive the phylogeographic signal in the data set. We trained two separate DAPC models: the first utilized the four phylogeographic clusters identified by principal components (PCs; fig. 6A and B and supplementary fig. S16 and table S1, Supplementary Material online); the second utilized the geographic localities where the samples were collected (i.e., countries in Europe and the U.S. states). This optimization indicated that the information contained in the first 40 PCs maximizes the probability of successful assignment (fig. 9A). This resulted in the inclusion of 30,000 GIMs, most of which were strongly associated with PCs 1–3 (fig. 9B inset). Moreover, the correlations were larger among the first 3 PCs and decayed monotonically for the additional PCs (fig. 9B). Lastly, our GIMs were uniformly distributed across the fly genome (fig. 9C).

Fig. 9.

Geographically informative markers. (A) Number of retained PCs which maximize the DAPC model’s capacity to assign group membership. Model trained on the phylogeographic clusters (dashed lines) or the country/state labels (solid line). (B) Absolute correlation for the 33,000 individual SNPs with highest weights onto the first 40 components of the PCA. Inset: Number of SNPs per PC. (C) Location of the 33,000 most informative demographic SNPs across the chromosomes. (D) LOOCV of the DAPC model trained on the phylogeographic clusters. (E) LOOCV of the DAPC model trained on the phylogeographic state/country labels. For panels (D) and (E), the y-axis shows the highest posterior produced by the prediction model and the x-axis is the posterior assigned to the actual label classification of the sample. Also, for (D) and (E), marginal histograms are shown.

We assessed the accuracy of our GIM panel using a leave-one-out cross-validation approach (LOOCV). We trained the DAPC model using all but one sample and then classified the excluded sample. We performed LOOCV separately for the phylogeographic cluster groups, as well as for the state/country labels. The phylogeographic model used all DrosRTEC, DrosEU, and DGN samples (excluding Asia and Oceania with too few individuals per sample); the state/country model used only samples for which each label had at least three or more samples. Our results showed that the model is 100% accurate in terms of resolving samples at the phylogeographic cluster level (fig. 9D) and 89% at the state/country level (fig. 9E). We anticipate that this set of GIMs will be useful to validate the geographic origin of samples in future sequencing efforts (i.e., identify sample swaps; Nunez et al. 2021) and to study patterns of migration. We note that although Drosophila populations evolve over short time-scales in temperate orchards, samples collected over multiple years were predicted with 89% accuracy in our LOOCV analysis, suggesting that these markers will be valuable for future samples. We provide a tutorial on the usage of the GIMs in supplementary methods, Supplementary Material online.

Estimating the Divergence Time between European Genetic Clusters

The DEST data set can be used to test comparative hypotheses of demographic history. We examined the divergence time between pairs of populations sampled throughout Europe. This is motivated by the observation that the two European clusters have different levels of genetic variation. The eastern cluster (E) is largely self-contained to Eastern Europe and harbors the lowest levels of θπ(0.0049, 95% CI = 0.0047–0.0050). The western cluster (W), on the other hand, contains populations from Western Europe as well as Finland, Turkey, Cyprus, and Egypt, thus making it geographically heterogeneous. The western cluster harbors higher levels of θπ relative to its eastern counterpart (0.0052, 95% CI = 0.0050–0.0054). Consequently, both clusters harbor statistically different levels of genetic variation (t-test; t-value = −5.22, degrees of freedom [df] = 332.96, P = 3.10×10-7), thus suggesting potentially different demographic histories. We tested whether the split time between eastern and western D. melanogaster populations was older than within clusters, and whether split time was positively correlated with geographic distance. Prior to addressing this hypothesis, we first evaluated the behavior of the PoolSNP and SNAPE-pooled data sets in demographic inference and also evaluated different methods for converting Pool-Seq data for use with site frequency spectrum-based analysis.

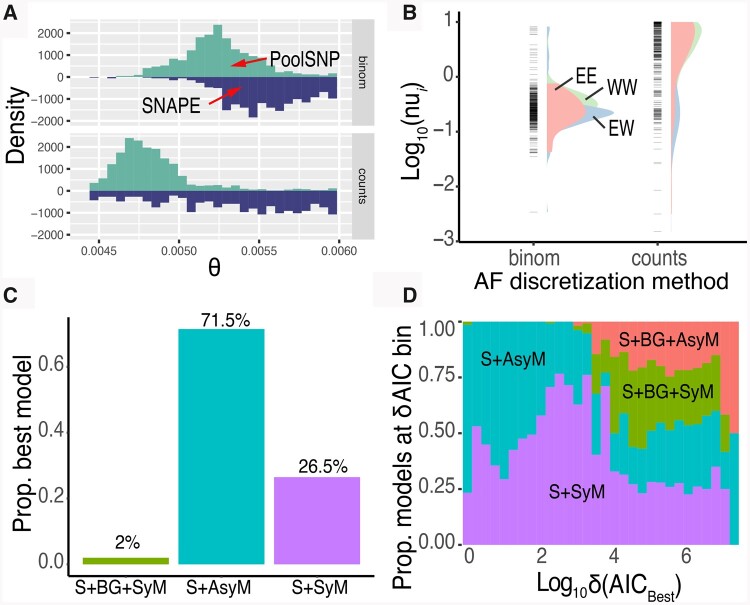
Prior to estimating divergence times between and among the European clusters, we assessed the behavior of our moment implementations using the summary statistic θ across models. We chose θ because it has a well-estimated value in D. melanogaster (θ=4Neμ=0.005; Lack et al. 2016) and thus can serve as a biologically informed calibration parameter. We conducted these preliminary assessments in our simplest model, S+SyM. Our results reveal conspicuous differences between SNAPE-pooled and PoolSNP. PoolSNP produces precise estimates of θ around the biological expectation, yet SNAPE-pooled estimates are imprecise and often converge to the bounds of the estimator (fig. 10A). This behavior is consistent for both AF discretization methods (binomial and counts). PoolSNP results also vary as a function of the AF discretization method. Based on these results, we chose to use only PoolSNP data for the implementation of our demographic inference.

Fig. 10.

Optimizing demographic models. (A) Estimates of θ from moments as a function of input data: PoolSNP (positive distribution) or SNAPE (negative distribution). We also show the AF discretization method (binomial, “binom,” top; counts, bottom). (B) Distribution of the parameter nui produced by moments as a function of AF discretization strategy. The three colors represent pairwise comparisons done within and across demographic clusters identified via PCA above. Specifically, pink: within eastern clusters (EE), blue: between clusters (EW), and green: within western clusters (WW). (C) Proportion of times a given model was determined to be the best according to AIC. (D) Distribution of δ(AICbest), the difference between the best model’s AIC, and all other evaluated models. The y-axis shows the proportion of time a given model appeared in a given δ(AICbest) bin. Because the models were Log10transformed, all values were shifted by +1 (to avoid Log10(0)=Undefined). Colors correspond to model type as labeled in the plot.

To further evaluate the behavior of PoolSNP’s estimates as a function of the AF discretization method, we explored values of the raw parameter outputs by moments. We explored the values of the nui parameter (the ancestral population size; see Materials and Methods). In general, the counts method produced nui estimates which are sparser and less stable, by an order of magnitude, relative to binomial draws (nui sdbinom=0.938, nui sdcounts=3.72). In addition, nui generated from the counts method produce highly skewed distributions, particularly for jSFS estimated for population pairs in eastern Europe (fig. 10B). Similar to SNAPE, estimates from the counts method also showed the problematic tendency to converge toward the parameter bounds (an example for nui is shown in fig. 10B). Thus, for the remainder of our analysis, we only report the binomial method.

We used AIC to test which of the four demographic models best fit the data: population divergence with symmetric migration (S+SyM), population divergence with asymmetric migration (S+AsyM), population divergence followed by a bottleneck and growth with symmetric migration (S+BG+SyM), or population divergence followed by a bottleneck and growth with asymmetric migration (S+BG+AsyM). We find that the S+AsyM was the best model 71.5% of the time, followed by S+SyM 26.6% of the time. Our more complex models (S+BG+SyM and S+BG+AsyM) were not generally favored by AIC (fig. 10C). We also evaluated δAIC, the difference in AIC between the best and all other models. We found that S+AsyM and S+SyM are generally the best models, whereas S+BG+SyM and S+BG+AsyM underperform by at least four orders of magnitude in terms of AIC (fig. 10D). We further evaluated AIC performance as a function of the number of completed runs. As described in the Materials and Methods, these demographic inferences are computationally expensive and not all models ran 50 times in the allotted time. This is of particular concern because all S+AsyM/SyM models ran 50 iterations, whereas S+BG+SyM/AsyM ran, on average, 44.7 and 35.2 times, respectively. As such, there is an inherent risk that the more complex models (S+BG+SyM/AsyM) did not find the best possible solution. We explored this possibility by partitioning δAIC as a function of the number of runs completed (supplementary fig. S17, Supplementary Material online). Our results indicate that the δAIC of the S+BG+SyM/AsyM does not improve among population pairs which run 40+ or the full 50 iteration cycles. This suggests that our AIC behavior is not a byproduct of the computational limit on iteration times. We also evaluated the residuals for the four demographic models, averaged across all population pairs that we contrasted (supplementary fig. S18, Supplementary Material online). These results show that, in general, all models slightly underestimate rare variants (<10%) and slightly overestimate variants between 10% and 35%. For the remainder of analysis, we used the S+AsyM model to estimate divergence times among populations.

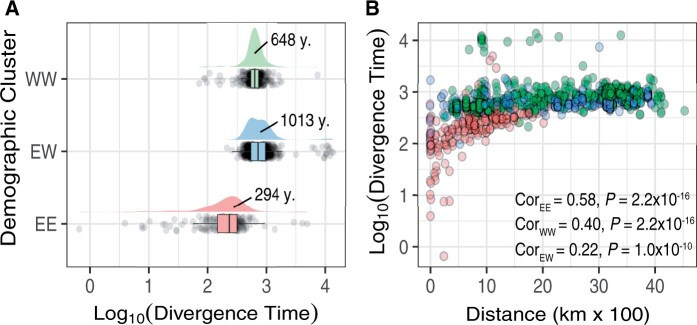
Our analyses suggest that the eastern and western demographic clusters diverged, on average, 1,013 years ago (95% CI = 887–1,139 years; median = 715 years; fig. 11A). Consistent with biological expectation, divergence estimates within population clusters were lower than between clusters. For example, the eastern cluster is estimated to have a mean divergence within populations of 294 years (95% CI = 225–362 years; median = 231 years). The western cluster has a mean divergence within populations of 648 years (95% CI = 627–668 years; median = 626 years). We evaluated the relationship between spatial distance and divergence time. Similar to our proximity analysis (fig. 8), the biological expectation is that populations in close proximity are likely to display low divergence estimates. Our results fit with this expectation, with neighboring populations within clusters displaying low divergence estimates (fig. 11B). Lastly, we estimated other population genetic parameters of these population clusters such as effective population size (N_E) and migration rates (M). Our estimates of N_E suggest that the western cluster has larger N_E (NE | west= 84,921; 95% CI = 83,373–86,468) relative to the eastern cluster (NE | east= 62,287; 95% CI = 60,207–64,368). In terms of asymmetrical migration rates between clusters, our findings show that the effective number of migrants per generation was higher for west-into-east migration (Mwest→east = 0.209 flies/gen; 95% CI = 0.169–0.250) as compared with the opposite direction (Meast→west = 0.178 flies/gen; 95% CI = 0.161–0.196).

Fig. 11.

Demographic inference of European clusters. (A) Estimates of divergence time between and within the European clusters, pink: within eastern clusters (EE), blue: between clusters (EW), and green: within western clusters (WW). (B) Divergence time as a function of the geographic distance between population pairs. Color palette is consistent with panel (A). Correlation values are shown in the figure.

Discussion

Here we have presented a new, modular, and unified bioinformatics pipeline for processing, integrating and analyzing SNP variants segregating in population samples of D. melanogaster. We have used this pipeline to assemble the largest worldwide data repository of genome-wide SNPs in D. melanogaster to date, based both on previously published data (DGN: Africa; Lack et al. 2015, 2016) as well as on new data collected by our two collaborating consortia (DrosRTEC: mostly North America; Machado et al. 2021; DrosEU: mostly Europe; Kapun et al. 2020). We assembled this data set using two SNP calling strategies that differ in their ability to identify rare polymorphisms, thereby enabling future work studying the evolutionary history of this species. We are dubbing this data repository and the supporting bioinformatics tools DEST.

The DEST data repository was built using two different SNP calling pipelines, SNAPE-pooled (Raineri et al. 2012) and PoolSNP (Kapun et al. 2020). These two methods differ fundamentally in their approach to SNP identification, yield data sets amenable to different types of analyses and each approach has its own specific limitations. The fundamental difference between the data sets produced by these methods is the number of rare and endemic SNPs identified. This difference will result in biased estimates of parameters from site frequency spectrum-based demographic models. As a consequence, some care should be taken when interpreting different analyses based on these data sets.

SNAPE-pooled treats each Pool-Seq sample separately and calculates the posterior probability that a site is polymorphic based on read depth, alternate allele count, and a prior estimate of nucleotide diversity; this approach was designed to identify rare polymorphisms and has been validated using both simulations and empirical approaches (Guirao-Rico and González 2021). Here, we also provide evidence that rare and private SNPs identified by SNAPE-pooled are enriched for true positives (fig. 8) after applying rigorous filtering and excluding 20 population samples likely affected by problems during library preparation which may have resulted in elevated error rates.

The dataset based on SNAPE-pooled could therefore be useful for studies that rely on rare SNPs, such as those investigating recent demographic events (Keinan and Clark 2012). SNAPE-pooled has several limitations though. First, it is only capable of handling Pool-Seq data. Second, because of the hard filtering that we are imposing with our posterior probability cut-off, some true SNPs are being called as missing data (see Materials and Methods). This problem is apparent when comparing the number of polymorphisms identified by SNAPE-pooled and PoolSNP (fig. 3). Third, any demographic inference done with SNAPE must be limited to cases where a SNP is discovered in at least three populations or more, because the caller appears to produce too many false positives when only two populations are considered (see fig. 8B and our demographic inference with moments, which uses a pairwise, two-population, model). In addition, studies that rely on the SNAPE-pooled data set should exclude the 20 samples we flagged here (fig. 2A and supplementary table S1, Supplementary Material online).

PoolSNP, on the other hand, is useful for analysis of common variants and allows studying aspects of population structure and local adaptation based on shared polymorphism. Such analyses could include the inference of migration out of Africa (Kapopoulou et al. 2020), admixture (Bergland et al. 2016), and back migration to Africa (Pool and Aquadro 2006). PoolSNP is an extension of the approach developed elsewhere (Kofler, Orozco-terWengel, et al. 2011; Kofler, Pandey, et al. 2011). PoolSNP necessarily has a limited capacity to identify rare and private SNPs because it imposes global MAC and allele frequency filters. Therefore, the more populations that are used for SNP calling by PoolSNP, the less likely PoolSNP is to identify private polymorphisms. Because PoolSNP filters out rare and private polymorphisms, it is less sensitive to sequencing or library preparation errors. Notably, the 20 flagged populations do not have elevated p_N/p_S with MAC > 50. Additionally, Kapun et al. (2020) demonstrated that these problematic samples did not affect population genetic inference based on common SNPs. The problematic samples derived from the DrosRTEC studies likely do not have a major impact on their results either as both Bergland et al. (2014) and Machado et al. (2021) imposed stringent MAF filters.

PoolSNP has the added advantage that it can incorporate in-silico pooled data sets wherein haplotype or genotype information are collapsed into allele frequencies (see Materials and Methods). We took this approach by incorporating the Drosophila Genome Nexus data set (DGN; Lack et al. 2016), a data set that amalgamates whole-genome sequencing of inbred line data and haploid embryos from samples collected around the world. Although the DGN data was originally generated by multiple labs and run through a different mapping pipeline than what we used for the Pool-Seq data, these samples appear to cluster tightly with geographically close Pool-Seq samples (supplementary fig. S15, Supplementary Material online and discussed in the Results). Thus, there does not appear to be significant bias when combining these data sets, at least when integrating information across the genome. Nonetheless, some care should be taken when interpreting allele frequency differences based on data sets generated by different means. However, any real-time monitoring activity will likely suffer from the rapidly changing landscape of sequencing technologies.

One of the biggest challenges in the present “omics” era is the rapidly growing number of complex large-scale data sets which require technically elaborate bioinformatics know-how to become accessible and utilizable. This hurdle often prohibits the exploitation of already available genomics data sets by scientists without a strong bioinformatics or computational background. To remedy this situation for the Drosophila evolution community, our bioinformatics pipeline is provided as a Docker image (to standardize across software versions, as well as make the pipeline independent of specific operating systems) and a new genome browser makes our SNP data set available through an easy-to-use web interface (see supplementary figs. S2 and S3, Supplementary Material online; available at https://dest.bio, last accessed September 6, 2021).

The DEST data repository and platform will enable the population genomics community to address a variety of longstanding, fundamental questions in ecological and evolutionary genetics. The current data set might for instance be valuable for providing a more accurate picture of the demographic history of D. melanogaster populations, in particular in Europe and North America, and with respect to multiple bouts of out-of-Africa migration and recent patterns of admixture. Such analyses can be strongly affected by chromosomal inversions that are known to impact LD and haplotype variation (Kapun and Flatt 2019; Durmaz et al. 2020). We have therefore provided frequency estimates for the seven most common cosmopolitan inversions (In(2L)t, In(2R)NS, In(3L)P, In(3R)C, In(3R)K, In(3R)Mo, and In(3R)Payne; Lemeunier and Aulard 1992), which allows accounting for the effects of inversions in population genetic inference (e.g., Kapopoulou et al. 2020).

The DEST data set will likewise be useful for an improved understanding of the genomic signatures underlying both global and local adaptation, including a more fine-grained view of selective sweeps, their evolutionary origin and distribution (e.g., see Glinka et al. 2003; Beisswanger et al. 2006; Ometto et al. 2005; Stephan 2016; Kapun et al. 2020). In terms of local adaptation, the broad spatial sampling across latitudinal and longitudinal gradients on the North American and European continents, encompassing a broad range of climate zones and areas of varying degrees of seasonality, will allow examining the parallel nature of local (clinal) adaptation in response to similar environmental factors in greater depth than possible before (e.g., Turner et al. 2008; Kolaczkowski et al. 2011; Fabian et al. 2012; Bergland et al. 2014, 2016; Reinhardt et al. 2014; Kapun et al. 2016, 2020; Waldvogel et al. 2020; Bogaerts‐Márquez et al. 2021; Machado et al. 2021).

Another major opportunity provided by the DEST data set lies in studying the temporal dynamics of evolutionary change. Sampling at dozens of localities across the growing season and over multiple years will help to advance our understanding of the short-term population and evolutionary dynamics of flies living in diverse environments, thereby providing novel insights into the nature of temporally varying selection (Bergland et al. 2014; Wittmann et al. 2017; Machado et al. 2021) and evolutionary responses to climate change (e.g., Umina 2005; Rodríguez-Trelles et al. 2013; Waldvogel et al. 2020).

Moreover, by integrating these worldwide estimates of allele frequencies, those from lab- and field-based “evolve and resequence” experiments (E&R; Turner et al. 2011; reviewed in Kofler and Schlötterer 2014; Schlötterer et al. 2014; Flatt 2020) and those from mesocosm experiments (e.g., Rudman et al. 2019; Erickson et al. 2020), we might be able to gain deeper insights into the genetic basis and evolutionary history of variation in fitness components (e.g., Flatt 2020).

In addition to analyses of selection, the DEST data set can also be used for preliminary demographic inference. Although Pool-Seq data sets lack important haplotype information, they have been successfully used in the past to generate demographic and biogeographic insights into both model and non-model species (e.g., Gautier et al. 2021; Machado et al. 2021; Nunez et al. 2021; see fig. 7). Our analyses suggest that Pool-Seq data can be used for demographic model inference. A major caveat in this endeavor is that, to the best of our knowledge, Pool-Seq has not been exhaustively benchmarked for demographic inference. As such, and until proper validation has been completed, we present our results as tools for hypothesis generation and exploration.

Our results from moments are in full agreement with basic biological expectations. For example, our estimates of θ are concordant with previously reported values (∼0.005; Lack et al. 2016). Moreover, our estimate of mean divergence time between the eastern and western European clusters of D. melanogaster is 1,013 years. This estimate is subject to caveats, given the nature of Pool-Seq data and that future validation may need to be done using different types of data. Nevertheless, we note that this value is plausible as it is well within the newer estimates for Drosophila’s expansion into Europe from Africa (4,139 years; Kapopoulou et al. 2020). Although previous studies estimated D. melanogaster’s European expansion to have occurred around 13,000 years ago (e.g., Li and Stephan 2006; Hutter et al. 2007; Laurent et al. 2011), Kapopoulou et al. (2020) showed that accounting for the role of asymmetric migration and admixture reduces the estimated divergence time between continents. Moreover, our mean estimates of NE for each cluster (NE | east= 62,287, NE | west= 84,921) are also within Kapopoulou et al.’s (2020) confidence interval for modern European D. melanogaster NE (67,444−633,186).

Our analyses also revealed two notable behaviors that are relevant to demographic analysis of Pool-Seq data. First, we observed a remarkable difference between the method used to discretize AFs from Pool-Seq, prior to SFS estimation. Discretizing the data based on direct counts results in noisier demographic estimates. Discretizing based on binomial probabilities, on the other hand, produced consistent results across comparisons. This behavior is due to the inherent noise of directly converting Pool-Seq AFs (which are heavily affected by coverage) to counts. Based on these observations, we recommend the use of the binomial method of AF discretization for Pool-Seq analysis (Thia and Riginos 2019). Second, we also observed a difference in the estimator’s behavior based on whether the PoolSNP or SNAPE-pooled data were used to build the SFS. In general, PoolSNP generated θ estimates which converge toward 0.005, the biological expectation for Drosophila. SNAPE-pooled estimates, on the other hand, produced θ distributions with high variance as well as a tendency to converge toward the edge of the prior. Interestingly, this type of run-to-the-edge pathological behavior has been previously characterized (Rosen et al. 2018) and is generally caused by two possible reasons: over-specified models, or, alternatively, noisy input SFS data. Given the relative simplicity of the model used for optimization (S+SyM; divergence with symmetrical-migration), it is likely that SNAPE’s SNP calling approach is producing a high number of false positives which affect model convergence (see also Geographic Proximity Analysis and fig. 8). We therefore recommend PoolSNP over SNAPE-pooled for the purposes of exploring or testing demographic hypotheses in cases where only two populations are considered.

Although our analyses of the DEST sequencing data already led to novel insights into the evolutionary history of Drosophila, we believe that the real value of the DEST data set lies in the future: its long-term utility will grow as natural and experimental populations are continually being sampled, re-sequenced and added to the repository by the community of Drosophila evolutionary geneticists. The pipeline that we have established will make future updates to the data repository straightforward. Furthermore, because it is not easily feasible for any single research group to sample flies densely through time and across a broad geographic range, the growing value of the DEST data set will depend upon the synergistic collaboration among research groups across the globe, as exemplified by the DrosRTEC and DrosEU consortia. Importantly, in an era of rapidly decreasing sequencing costs, comprehensive population genomic analyses are no longer limited by genetic marker density but by the availability of biological samples from standardized, collaborative long-term collection efforts through space and time (e.g., Kapun et al. 2020; Machado et al. 2021). In this vein, the collaborative framework presented here might allow us, as a global community, to fill some important gaps in the current data repository: for example, many areas of the world (notably Asia and South America) remain largely uncharted territory in Drosophila population genomics, and the addition of phased sequencing data (e.g., providing information on haplotypes, LD, linked selection) will be crucially important for future analyses of demography, selection, and their interplay.

We are convinced that the DEST platform will become a valuable and widely used resource for scientists interested in Drosophila evolution and genetics, and we actively encourage the community to join the collaborative effort we are seeking to build.

Materials and Methods

Data Sources

The genomic data set presented here has been assembled from a combination of Pool-Seq libraries and in silico pooled haplotypes. We combined 246 Pool-Seq libraries of population samples from Europe, North America, and the Caribbean that were sampled through space and time by two collaborating consortia in North America (DrosRTEC: https://web.sas.upenn.edu/paul-schmidt-lab/dros-rtec/, last accessed September 6, 2021) and Europe (DrosEU: http://droseu.net, last accessed September 6, 2021) between 2003 and 2016. Of these 246 Pool-Seq samples, 121 samples represent previously unpublished samples generated by DrosEU, 48 DrosEU samples previously reported in Kapun et al. (2020), and 77 samples previously reported in Machado et al. (2021). In addition, we integrated genomic data from >900 inbred or haploid genomes from 25 populations in Africa, Europe, Australia, and North America available from the Drosophila Genome Nexus data set (DGN v1.1; Pool et al. 2012; Langley et al. 2012; Grenier et al. 2015; Kao et al. 2015; Lack et al. 2015, 2016) We further included the D. simulans haplotype (w⁵⁰¹; Hu et al. 2013), built as part of the DGN data set, as an outgroup, making this repository of 272 (246 Pool-Seq + 25 DGN + 1 D. simulans) whole-genome sequenced samples the largest data set of genome-wide SNP polymorphisms available for D. melanogaster to date.

Metadata

We assembled uniform metadata for all samples (supplementary table S1, Supplementary Material online). This information includes collection coordinates, collection date, and the number of flies per sample. Samples are also linked to bioclimatic variables from the nearest WorldClim (Hijmans et al. 2005) raster cell at a resolution of 2.5° and to weather stations from the Global Historical Climatology Network (GHCND; ftp://ftp.ncdc.noaa.gov/pub/data/ghcn/daily/) to allow for future analyses of the environmental drivers that might underlie genetic change. We also provide summaries of basic attributes of each sample derived from the sequencing data including average read depth, PCR duplicate rate, D. simulans contamination rate, relative abundances of non-synonymous versus synonymous polymorphisms (p_N/p_S), the number of private polymorphisms, diversity statistics (Watterson’s θ, π, and Tajima’s D), and estimates of inversion frequencies.

Sample Collection

Most population samples contributed by the DrosEU and the DrosRTEC consortia were collected in a coordinated fashion to generate a consistent data set with minimized sampling bias. In brief, fly collections were performed exclusively in natural or seminatural habitats, such as orchards, vineyards, and compost piles. For most European collections, flies were collected using mashed banana, or apples with live yeast as bait in traps placed at sampling sites for multiple days to attract flies, or by sweep netting (see Kapun et al. 2020 for more details). For North American collections, flies were collected by sweep-net, aspiration, or baiting over natural substrate or using baited traps (see Behrman et al. 2018; Machado et al. 2021 for details). Samples were either field-caught flies (n = 227), from F1 offspring of wild-caught females (n = 7), from a mixture of F1 and wild-caught flies (n = 7), or from flies kept as isofemale lines in the laboratory for five generations or less (n = 4); see supplementary table S1, Supplementary Material online for more information. To minimize cross-contamination with the closely related sympatric sister species D. simulans, we only sequenced male D. melanogaster specimens, allowing for higher confidence discrimination between the two species based on the morphology of male genitalia (Capy and Gibert 2004; Markow and O’Grady 2006). Samples were stored in 95% ethanol at −20°C before DNA extraction.

DNA Extraction and Sequencing

The DrosEU and DrosRTEC consortia centralized extractions from pools of flies. DNA was extracted either using chloroform/phenol-based (DrosEU: Kapun et al. 2020) or lithium chloride/potassium acetate extraction protocols (DrosRTEC: Bergland et al. 2014; Machado et al. 2021) after homogenization with bead beating or a motorized pestle. DrosEU samples from the 2014 collection were sequenced on an Illumina NextSeq 500 sequencer at the Genomics Core Facility of the Pompeu Fabra University in Barcelona, Spain. Libraries of the previously unpublished DrosEU samples from 2015 and 2016 were constructed using the Illumina TruSeq PCR Free library preparation kit following the manufacturer’s instructions and sequenced on the Illumina HiSeq X platform as paired-end fragments with 2 × 150 bp length at NGX Bio (San Francisco, California, USA). The previously published samples of the DrosRTEC consortium were prepared and sequenced on GAIIX, HiSeq2000, or HiSeq3000 platforms, as described in Bergland et al. (2014) and Machado et al. (2021). For information on DNA extraction and sequencing methods of the various DGN samples, see Lack et al. (2016) and others (Langley et al. 2012; Pool et al. 2012; Grenier et al. 2015; Kao et al. 2015).

Mapping Pipeline

The joint analysis of genomic data from different sources requires the application of uniform quality criteria and a common bioinformatics pipeline. To accomplish this, we developed a standardized pipeline that performs filtering, quality control and mapping of any given Pool-Seq sample (see supplementary fig. S1, Supplementary Material online). This pipeline performs quality filtering of raw reads, maps reads to a hologenome (see below), performs realignment and filtering around indels, and filters for mapping quality. The output of this pipeline includes quality control metrics, bam files, pileup files, and allele frequency estimates for every site in the genome (gSYNC, see below). Our pipeline is provided as a Docker image and will facilitate the integration of future samples to extend the worldwide D. melanogaster SNP data set presented here.

The mapping pipeline includes the following major steps. Prior to mapping, we removed sequencing adapters and trimmed the 3′ ends of all reads using cutadapt (Martin 2011). We enforced a minimum base quality score ≥18 (-q flag in cutadapt) and assessed the quality of raw and trimmed reads with FASTQC. Trimmed reads with minimum length <75 bp were discarded and only intact read pairs were considered for further analyses. Overlapping paired-end reads were merged using bbmerge (v. 35.50; Bushnell et al. 2017). Trimmed reads were mapped against a compound reference genome (“hologenome”) consisting of the genomes of D. melanogaster (v.6.12) and D. simulans (Hu et al. 2013) as well as genomes of common commensals and pathogens, including Saccharomyces cerevisiae (GCF_000146045.2), Wolbachia pipientis (NC_002978.6), Pseudomonas entomophila (NC_008027.1), Commensalibacter intestine (NZ_AGFR00000000.1), Acetobacter pomorum (NZ_AEUP00000000.1), Gluconobacter morbifer (NZ_AGQV00000000.1), Providencia burhodogranariea (NZ_AKKL00000000.1), Providencia alcalifaciens (NZ_AKKM01000049.1), Providencia rettgeri (NZ_AJSB00000000.1), Enterococcus faecalis (NC_004668.1), Lactobacillus brevis (NC_008497.1), and Lactobacillus plantarum (NC_004567.2), using bwa mem (v. 0.7.15; Li 2013) with default parameters. We retained reads with mapping quality greater than 20 as well as those with no secondary alignment using samtools (Li et al. 2009). PCR duplicate reads were removed using Picard MarkDuplicates (v.1.109; http://broadinstitute.github.io/picard/, last accessed September 6, 2021). Sequences were realigned in the proximity of insertions–deletions (indels) with GATK (v3.4-46; McKenna et al. 2010). We identified and removed any reads that mapped to the D. simulans genome using a custom python script, following methods outlined previously (Kapun et al. 2020; Machado et al. 2021; for a more in-depth analysis of D. simulans contamination, see Wallace et al. 2021). Although this method of decontamination by D. simulans accurately estimates contamination rate and removes the vast majority of D. simulans reads (Machado et al. 2021), care should be taken when analyzing samples with higher contamination rates at sites that are shared polymorphisms between the two species.

Incorporation of the DGN Data Set

We incorporated population allele frequency estimates derived from inbred line and haploid embryo sequencing data from populations sampled throughout the world using an in silico pooling approach. These samples have been previously collected and sequenced by several groups (Langley et al. 2012; Mackay et al. 2012; Pool et al. 2012; Grenier et al. 2015; Kao et al. 2015; Lack et al. 2015, 2016) and together form the Drosophila Genome Nexus data set (DGN; Lack et al. 2015, 2016). We included 25 DGN populations with ≥5 individuals per population, plus the D. simulans haplotype w⁵⁰¹ built as part of the DGN data set. The DGN populations that we used are primarily from Africa (n = 18) but also include populations from Europe (n = 2), North America (n = 3), Australia (n = 1), and Asia (n = 1). The complete list of DGN populations, and samples, used in this data set can be found in supplementary table S1, Supplementary Material online.

To incorporate the DGN populations into the DrosEU and DrosRTEC Pool-Seq data sets, we used the pre-computed FASTA files (“Consensus Sequence Files” from https://www.johnpool.net/genomes.html, last accessed September 6, 2021) and calculated allele frequencies at every site, for each population, using custom bash scripts. We calculated allele frequencies for each population by summing reference and alternative allele counts across all individuals using the precomputed haplotype FASTA files. Because estimates of allele frequencies and total allele counts for the DGN samples only consider unambiguous IUPAC codes, heterozygous sites or sites masked as N’s in the original FASTA files were converted to missing data. We used liftover (Kuhn et al. 2013) to translate genome coordinates to Drosophila reference genome release 6 (dos Santos et al. 2015) and formatted them to match the gSYNC format (described below). Scripts for reformatting the DGN data can be found in the GitHub repository for this project (https://github.com/DEST-bio/DEST_freeze1, last accessed September 6, 2021).

SNP Calling Strategies

We used two complementary approaches to perform SNP calling. The first was PoolSNP (Kapun et al. 2020), a heuristic tool which identifies polymorphisms based on the combined evidence from multiple samples. This approach is similar to other common Pool-Seq variant calling tools (Koboldt et al. 2009, 2012; Kofler, Orozco-terWengel, et al. 2011; Kofler, Pandey, et al. 2011). PoolSNP integrates allele counts across multiple independent samples and applies stringent MAC and MAF thresholds for variant detection. PoolSNP is expected to be good at detecting variants present in multiple populations but is not very sensitive to rare private alleles. The second approach was SNAPE-pooled (Raineri et al. 2012), a tool that identifies polymorphic sites based on Bayesian inference for each population independently using pairwise nucleotide diversity estimates as a prior. SNAPE-pooled is expected to be more sensitive to rare private polymorphisms (Raineri et al. 2012; Guirao-Rico and González 2021). The SNP calling step is built using the snakemake (Mölder et al. 2021) pipeline and the parameters to run the two callers can be found at https://github.com/DEST-bio/DEST_freeze1 (last accessed September 6, 2021).

gSYNC Generation and Filtering

Our pipeline utilizes a common data format to encode allele counts for each population sample (SYNC; Kofler, Pandey, et al. 2011). A “genome-wide SYNC” (gSYNC) file records the number of A, T, C, and G for every site of the reference genome. Because gSYNC files for all populations have the same dimension, they can be quickly combined and passed to a SNP calling tool. They can be filtered and are also relatively small for a given sample (∼500 Mb), enabling efficient data sharing and access. The gSYNC file is analogous to the gVCF file format as part of the GATK HaplotypeCaller approach (McKenna et al. 2010) but is specifically tailored to Pool-Seq samples.

We generated gSYNC files for both PoolSNP and SNAPE. To generate a PoolSNP gSYNC file, we first converted BAM files to the MPILEUP format with samtools mpileup using the -B parameter to suppress recalculations of per-base alignment qualities and filtered for a minimum mapping quality with the parameter -q 25. Next, we converted the MPILEUP file containing mapped and filtered reads to the gSYNC format using custom python scripts. To generate a SNAPE-pooled gSYNC file, we ran the SNAPE-pooled version specific to Pool-Seq data for each sample in MPILEUP format with the following parameters: θ = 0.005, D = 0.01, prior=‘informative’, fold=‘unfolded’, and nchr=number of flies (x2 for autosomes and x1 for the X and Y chromosomes) following Guirao-Rico and González (2021). We converted the SNAPE-pooled output file to a gSYNC file containing the counts of each allele per position and the posterior probability of polymorphism as defined by SNAPE-pooled using custom python scripts. We only considered positions with a posterior probability ≥0.9 as being polymorphic and with a posterior probability ≤0.1 as being monomorphic. In all other cases, positions were marked as missing data.

We masked gSYNC files for PoolSNP and SNAPE-pooled using a common set of filters. Sites were filtered from gSYNC files if they had: 1) minimum read depth <10; 2) maximum read depth >the 95% coverage percentile of a given chromosomal arm and sample; 3) located within repetitive elements as defined by RepeatMasker; 4) within 5-bp distance up- and downstream of indel polymorphisms identified by the GATK IndelRealigner. Filtered sites were converted to missing data in the gSYNC file. The location of masked positions for every sample was recorded as a BED file.

VCF Generation

We generated three versions of the variant files, which differ in their inclusion of the DGN samples and the SNP calling strategy. For PoolSNP variant calling, we generated two variant tables: the first version incorporates all 272 samples of the Pool-Seq (DrosRTEC, DrosEU) and in silico Pool-Seq populations (DGN). The second version only considers the 246 Pool-Seq samples excluding the DGN samples (used for comparison to the SNAPE-pooled version). The third file is based on SNAPE-pooled and contains 246 Pool-Seq samples only.

To generate the PoolSNP versions, we combined the masked PoolSNP-gSYNC files into a two-dimensional matrix, where rows correspond to each position in the reference genome and columns describe chromosome, position, and reference allele, followed by allele counts in SYNC format for every sample in the data set. This combined matrix was then subjected to variant calling using PoolSNP, resulting in a VCF-formatted file. We performed SNP calling only for the major chromosomal arms (X, 2L, 2R, 3L, 3R) and the 4th (dot) chromosome. Data for heterochromatic arms of the autosomes, the Y chromosome, and the mitochondrial genome can be extracted from the MPILEUP files provided at https://dest.bio (last accessed September 6, 2021).

We evaluated the choice of two heuristic parameters applied to PoolSNP: global MAC and global MAF. Using all 272 samples, we varied MAF (0.001, 0.01, 0.05) and MAC (5-100) and called SNPs at a randomly selected 10% subset of the genome. Based on SNP annotations with SNPeff (version 4.3; Cingolani et al. 2012), we calculated p_N/p_S, which is the ratio of nonsynonymous to synonymous polymorphisms, and used this value to tune our choice of MAF and MAC and to identify egregious outlier samples. We found that a global MAC = 50 provided qualitatively identical estimates of p_N/p_S across all populations (fig. 2B) and that the results were insensitive to MAF (results not shown). We therefore used these parameters for genome-wide variant calling (see Identification and Quality Control of SNP Polymorphisms). We kept a third heuristic parameter, the missing data rate, constant at a minimum of 50%.

To generate the SNAPE-pooled VCF files, we combined the 246 masked SNAPE-pooled gSYNC files into a two-dimensional matrix, as described above, and generated a VCF formatted output based on allele counts for any site found to be polymorphic in one or more populations. We evaluated p_N/p_S across a range of local MAF thresholds (fig. 2C) and found that p_N/p_S is largely insensitive to local MAF, once accounting for some problematic samples (see below).

Final VCF files with annotations from SNPeff (version 4.3; Cingolani et al. 2012) were stored in VCF and BCF (Danecek et al. 2011) file formats alongside an index file in TABIX format (Li 2011). Besides VCF files, we also stored SNP data in the GDS file format using the R package SeqArray (Zheng et al. 2017).

Inversion Frequency Estimates

We estimated the frequencies of seven cosmopolitan inversion polymorphisms (In(2L)t, In(2R)NS, In(3L)P, In(3R)C, In(3R)K, In(3R)Mo, In(3R)Payne) based on a previously published panel of diagnostic SNP markers that are in tight LD with the corresponding inversions (Kapun et al. 2014). As previously described (Kapun et al. 2016), we isolated the positions in the VCF file of all marker SNPs and estimated the frequency of each inversion as the mean frequency of inversion-specific alleles at all marker SNPs.

Population Genetic Analyses

We estimated allele frequencies for each site across populations as the ratio of the alternate allele count to the total site coverage. We also calculated per-site averages for nucleotide diversity (π, Nei 1987), Watterson’s θ (Watterson 1975) and Tajima’s D (Tajima 1989) across all sites or in nonoverlapping windows of 100, 50, and 10 kb length. To estimate these summary statistics, we converted masked gSYNC files (with positions filtered for repetitive elements, low and high read depth, and proximity to indels; see gSYNC Generation and Filtering) back to the MPILEUP format using custom-made scripts. The MPILEUP files were processed using npstat v.1 (Ferretti et al. 2013) with parameters -maxcov 10000 and -nolowfreq m = 0 in order to include all filtered positions for analysis. We only considered sites identified as being polymorphic by PoolSNP or SNAPE-pooled for analysis, using the -snpfile option of npstat. For the DGN populations, chromosome-wide summary statistics were estimated only for samples with less than 50% missing data per chromosome. Due to small sample sizes, Tajima’s D was not estimated for seven African DGN populations that consisted of only five haploid embryos. To compare population genetic estimates between the PoolSNP versus SNAPE-pooled data sets, we performed Pearson’s correlation on 226 populations present in both data sets (see Identification and Quality Control of SNP Polymorphisms) using the stats package of R v.3.6.3. The effects of pool size (number of individuals sampled per population) on genome-wide estimates of π, Watterson’s θ and Tajima’s D_S estimates were examined for European and North American populations using the PoolSNP data set and a linear model in R v.3.6.3. Finally, for 48 European populations we estimated Pearson’s correlations between π, Watterson’s θ and Tajima’s D as estimated from the PoolSNP data set versus previous estimates by Kapun et al. (2020) using the stats package of R v3.6.3.

Next, we examined patterns of between-population differentiation by calculating window-wise estimates of pairwise F_ST, based on the method from Hivert et al. (2018) implemented in the computePairwiseFSTmatrix() function of the R package poolfstat (v1.1.1). This analysis was performed for the data set composed of 271 samples (all samples excluding the D. simulans reference strain) processed with PoolSNP, focusing on SNPs shared across the whole data set. Finally, we averaged pairwise F_ST within and among phylogeographic clusters identified in our analyses: Africa (17 samples), North America (76 samples), Eastern Europe (83 samples), and Western Europe (93 samples). Samples from China and Australia were not included due to limited sampling. These F_ST tracks at windows sizes of 100, 50, and 10 kb are available at https://dest.bio (last accessed September 6, 2021; supplementary figs. S2 and S3, Supplementary Material online).

To assess population structure in the worldwide data set, we applied principal components analysis (PCA), population clustering, and population assignment based on a DAPC (Jombart et al. 2010) to all 271 PoolSNP-processed samples. For these analyses, we subsampled a set of 100,000 SNPs spaced apart from each other by at least 500 bp. We optimized our models using cross-validation by iteratively dividing the data as 90% for training and 10% for learning. We extracted the first 40 PCs from the PCA and ran Pearson’s correlations between each PC and all loci. We subsequently extracted the top 33,000 SNPs with large and significant correlations to PCs 1–40. We chose the 33,000 number as a compromise between panel size and differentiation power. For example, depending on the number of individuals surveyed, these 33,000 loci can discern genetic differentiation (τ) between two populations with parametric F_ST of 0.001–0.0001 for sample sizes (n) of 10–1,000. These estimates come from the phase change formula: τ ≈ F_ST = 1/(nm)^1/2 (Patterson et al. 2006). Here, the two populations were sampled for n/2 individuals and genotyped at m = 33,000 markers. Furthermore, we included SNPs as a function of the percent variance explained by each PC. PCAs, clustering, and assignment based DAPC analyses were carried out using the R packages FactoMiner (v. 2.3), factoextra (v. 1.0.7) and adegenet (v. 2.1.3), respectively.

Demographic Inference with Moments

To evaluate the efficacy of PoolSNP and SNAPE-pooled in inferring reasonable demographic parameters, we ran pairwise comparisons of European Drosophila populations under four basic demographic models: 1) population divergence with symmetric migration (S+SyM), 2) population divergence with asymmetric migration (S+AsyM), 3) population divergence followed by a bottleneck and growth with symmetric migration (S+BG+SyM), and 4) population divergence followed by a bottleneck and growth with asymmetric migration (S+BG+AsyM). We fit these models using the python package moments (Jouganous et al. 2017). We converted our data to the moments input format using the genomalicious (Thia and Riginos 2019) function dadi_inputs_pools(), using either the “counts” or the “probs” (hereafter “binomial”) methods. These methods are used to convert Pool-Seq allele frequency data, which has a variable denominator (read depth), to the integer-based count of the site frequency spectrum (SFS) used by moments and other SFS analyses (Gutenkunst et al. 2009). The “counts” method rounds the allele counts to the nearest integer based on the number of chromosomes sampled. The “binomial” method generates allele counts based on a binomial draw given the observed allele frequency and the number of chromosomes. For all analyses, we used the mean effective coverage (Feder et al. 2012) per population as the number of chromosomes sampled. We only focused on autosomal SNPs and only used populations that passed quality control (fig. 2).

Our model estimates a different number of parameters depending on its type. For instance, the S+SyM model estimates three core parameters: the divergence time between populations (Ts), the migration rate between populations (mi↔j) and the ancestral population sizes (nui). The nui, Ts and mi↔j parameters are initially drawn from uniform priors with user-defined upper boundaries of 10, 5, and 50, and lower boundaries of 1.0×10-5, 1.0×10-5, and 0, respectively. The S+AsyM model includes all above parameters, but has explicit asymmetric migration parameters (i.e., mi→j and mj→i) which are also parametrized as uniform distributions with 0–50 parameter bounds. Models S+BG+SyM and S+BG+AsyM are similar to their S+AsyM and S+SyM counterparts, with the addition of the initial (nuiB) and final (nuiF) sizes of each population. These are also parametrized as uniform distribution bounded between 1.0×10-5 and 10. Overall, we explored the behavior of the estimators for two allele frequency (AF) discretization strategies (counts and binomial) and two SNP callers (SNAPE and PoolSNP).

Our pipeline estimates a joint SFS (jSFS) from the discretized AF data for a given population pair. These are always folded jSFS to account for unknown ancestral states. For computational purposes, we did not evaluate every possible pairwise combination in the DEST data set. Instead, we randomly sampled 1,200 population pairs drawn from European populations that passed quality filtering (supplementary table S1, Supplementary Material online). The moments simulations were run with a maximum of 50 iterations. It is important to note that running these demographic models is computationally expensive and some individual runs fail to converge across the 50 iterations, and thus some models did not run all 50 times. Nevertheless, we explicitly explored the consequences of the total number of completed runs in the performance of the model selection.

Model selection was performed using maximum log-likelihood and Akaike’s information criterion (AIC) for each completed simulation run. For each implementation per population pair, the simulation with lowest AIC was retained as the “best fit” for later comparison. The model fit was observed in a subset of models run via residuals as well. Raw model parameter outputs were converted to interpretable units in accordance with the moments manual. To this end, we used known biological constants for Drosophila, namely μ, L, and generations per year (g). The mutation rate, μ, was set to 2.8×10-9 (Keightley et al. 2014). L is the sum of the autosomal chromosome arms minus the median of the number of masked sites across all of the European (DrosEU) samples. In moments, outputs are scaled in units of 2Nref, where Nref is the ancestral population size (Nref =θ/4μL). Divergence time (2Nref Ts) was converted to chronological time assuming 15 generations per year (Pool 2015).

Web-Based Genome Browser

Our HTML-based DEST browser (supplementary fig. S2, Supplementary Material online) is built on a JBrowse Docker container (Buels et al. 2016), which runs under Apache on a CentOS 7.2 Linux x64 server with 16 Intel Xeon 2.4 GHz processors and 32 GB RAM. It implements a hierarchical data selector that facilitates the visualization and selection of multiple population genetic metrics or statistics for all 271 samples based on the PoolSNP-processed data set, taking into account sampling location and date. Importantly, our genome browser provides a portal for downloading allelic information and precomputed population genetics statistics in multiple formats (supplementary figs. S2A and C and S3, Supplementary Material online), a usage tutorial (supplementary fig. S2B, Supplementary Material online) and versatile track information (supplementary fig. S2D, Supplementary Material online). Bulk downloads of full variation tracks are available in BigWig format (Kent et al. 2010) and Pool-Seq files (in VCF format) are downloadable by population and/or sampling date using custom options from the Tools menu (supplementary fig. S2C, Supplementary Material online). All data, tools, and supporting resources for the DEST data set, as well as reference tracks downloaded from FlyBase (v.6.12) (dos Santos et al. 2015), are freely available at https://dest.bio (last accessed September 6, 2021).

Supplementary Material

Supplementary data are available at Molecular Biology and Evolution online.