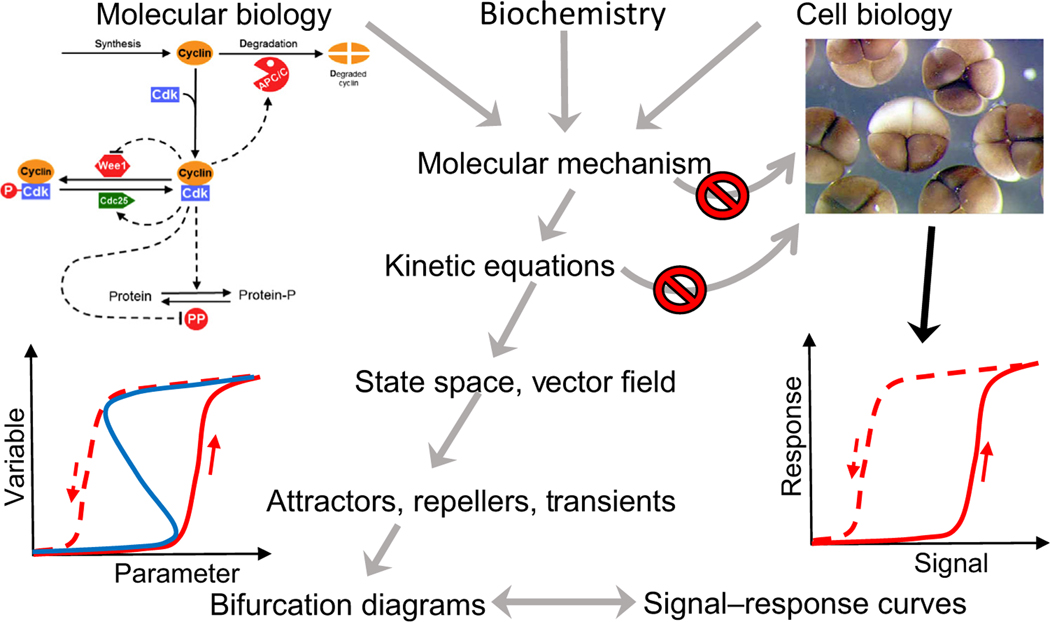
Figure 2. Key Figure A Dynamical Paradigm for Molecular Cell Biology.

Biologists gather information from many types of experiments to propose a molecular mechanism for the control of some aspect of cell physiology; for example, the regulation of cyclin-dependent kinase (upper left) as an explanation of the early embryonic divisions of frog eggs (upper right). Nowadays, these mechanisms are so complex that intuitive arguments alone are insufficient to understand the full behavioral repertoire of cells (the ‘curse of complexity’, represented by the upper ‘no passage’ sign). In principle, one could convert the mechanism into a set of differential equations and use computer simulations to deduce the temporal responses of cells to signals (lower right), but this approach is stymied by our ignorance of the values of the rate constants and binding constants that enter into the kinetic equations (the ‘curse of parameter space’ – the lower ‘no passage’ sign). The curses can be bypassed by ‘dynamical systems theory’ which considers kinetic equations as defining a vector field in state space (Figure 1). The vector field defines key attractors, repellers, and transients of the dynamical system, which can be characterized by a one-parameter bifurcation curve (lower left) The theoretician’s bifurcation curve is directly comparable with the physiologist’s signal–response curve. By making this connection, dynamical systems theorists can work their way backward to the parameter values that are necessary to account for the signal–response characteristics of the cells, and from there to comprehensive simulations of the molecular mechanism under a variety of experimental conditions, including novel tests of the model. Abbreviation: P, phosphorylation.