Abstract
This paper examines a combined supervised-unsupervised framework involving dictionary-based blind learning and deep supervised learning for MR image reconstruction from under-sampled k-space data. A major focus of the work is to investigate the possible synergy of learned features in traditional shallow reconstruction using adaptive sparsity-based priors and deep prior-based reconstruction. Specifically, we propose a framework that uses an unrolled network to refine a blind dictionary learning-based reconstruction. We compare the proposed method with strictly supervised deep learning-based reconstruction approaches on several datasets of varying sizes and anatomies. We also compare the proposed method to alternative approaches for combining dictionary-based methods with supervised learning in MR image reconstruction. The improvements yielded by the proposed framework suggest that the blind dictionary-based approach preserves fine image details that the supervised approach can iteratively refine, suggesting that the features learned using the two methods are complementary.
Keywords: Magnetic resonance image reconstruction, deep learning, dictionary learning, inverse problems, unrolled neural networks, sparse representations
I. Introduction
Reconstruction of images from limited measurements requires solving an ill-posed inverse problem. In such problems, additional regularization is typically used. Often, such regularization reflects ‘prior’ knowledge about the class of images being reconstructed. Traditional regularizers exploit the sparsity of images in some domains [1], [2], or low-rankness [3], [4]. Compared to using a fixed regularizer, such as total variation (TV) or wavelet sparsity-based regularization, data-driven or adaptive regularization has proven to be very beneficial in several applications [5]-[10]. In this form of reconstruction, one or more components of the regularizer, such as a dictionary or sparsifying transform, are learned from data adaptively, rather than being fixed to mathematical models like the discrete cosine transform (DCT) or wavelets. In particular, methods that exploit the sparsity of image patches in a learned transform domain or express image patches as a sparse linear combination of learned dictionary atoms have found widespread use in regularized MR image reconstruction [11]-[15].
A subset of this class of adaptive reconstruction algorithms relies only upon the measurements of the image being reconstructed to learn dictionaries or transforms, and uses no additional training data. These methods are dubbed blind learning-based reconstruction algorithms or blind compressed-sensing methods [16], [17]. One advantage of patch-based dictionary-blind reconstruction algorithms is that they do not require much (or any) training data to operate, and effectively leverage unique patterns present in the underlying data.
With the success of deep-learning-based methods for computer vision and natural language processing, there has also been a rise in methods that use neural networks to “regularize” (often in implicit manner) MRI reconstruction problems [18]-[22]. Some works treat reconstruction as a domain adaptation problem similar to style transfer and in-painting [23]-[26]. Correspondingly, image refinement networks, such as the U-net [27], were adopted to correct the aliasing artifacts of the under-sampled input images. Although such CNN-based reconstruction methods achieved improved results compared to compressed sensing (CS) based reconstruction, the stability and interpretability of these models is a concern [28].
Besides improvements through algorithms, another driving force for supervised learning-based reconstruction is the curation of publicly available datasets for training. The availability of pairwise training data owing to initiatives like [29], [30] has further helped showcase the ability of deep learning-based algorithms for extracting or representing image features, and in learning richer models for image reconstruction in MR applications. These methods, due to their reliance on pixel-wise supervision perform exclusively supervised learning-based reconstruction, barring a few exceptions [31], [32].
Consequently, due to the popularity and computational efficiency of deep learning approaches across MRI applications, there has been a rising trend of favoring deep supervised methods over shallower dictionary-based methods—perhaps because the latter methods use “handcrafted” priors.
The rising popularity of supervised deep learning compared to shallow blind-dictionary learning may be based on an underlying assumption that the features learned using relatively unrestricted supervised deep models subsume those learned in a blind fashion, and other sparsity-based priors that are deemed “handcrafted”. Though supervised deep-learned regularization may allow for the learning of richer models in reconstructing MR images, the aforementioned assumption is largely untested. Moreover, deep CNNs often require relatively large datasets to train well. This paper seeks to address these issues.
This work studies the processes of blind learning-based and supervised learning-based MRI reconstruction from undersampled data, and highlights the complementarity of the two approaches by proposing a framework that combines the two in a residual fashion. We implement and compare multiple approaches for combining supervised and blind learning.
Our results indicate that supervised and dictionary-based blind learning may learn complementary features, and combining both frameworks using “BLInd Primed” Supervised (BLIPS) learning can significantly improve reconstruction quality. In particular, the combined reconstruction better preserves fine higher-frequency details that are very important in many clinical settings. We also find that this improvement from combining blind and supervised learning is relatively robust to changes in training dataset size, and across different imaging protocols.
The rest of this paper is organized as follows. Section II describes the blind and supervised learning-based approaches and the proposed strategies for combining them. Section III details the experiment settings, including datasets, hyperparameters, and control methods. Section IV presents the results and Section V provides related discussion. Finally, Section VI explains our conclusions and plans for future work.
II. Problem Setup and Algorithms
This work combines two modern approaches to MR image reconstruction: dictionary-based blind learning reconstruction and CNN-based supervised learning reconstruction. The former approach capitalizes on the sparsity of natural images in an adaptive dictionary model. Usually, this method involves expressing patches in the MR image as a linear combination of a small subset of atoms or columns of a dictionary. Across several applications, including MR image reconstruction, learned or adaptive dictionaries often provide better representations of signals than fixed dictionaries. When these dictionaries are learned from the image being reconstructed, using no additional information, they are called blind, and can be considered to be ‘tailored’ specifically to the reconstruction at hand. Since individual image patches are approximated by different atoms, overcomplete dictionaries are often preferred for this approach because of their ability to provide richer representations of data.
For supervised learning reconstruction, this paper uses an unrolled network algorithm similar to the state-of-the-art method MoDL [20], whose variants have achieved top performance in recent open data-driven competitions in MR reconstruction [18], [33]. As ‘unrolled’ implies, the method consists of multiple iterations or blocks. In each iteration, a CNN-based denoiser updates the image from the previous iteration. A subsequent data-consistency update ensures the reconstructed image is consistent with the acquired k-space measurements. By incorporating CNNs into iterative reconstruction, MoDL demonstrates improved reconstruction quality and stability compared to other direct inversion networks on large public datasets [18].
Given a set of k-space measurements , c = 1, …, Nc, from Nc coils with corresponding system matrices , c = 1, …, Nc, this section reviews the procedures of reconstruction using blind and supervised learning, and then proposes a method for combining them, along with a few special cases. We write the system matrix for the cth coil as , where P ∈ {0, 1}p×q incorporates the mask that describes the sampling pattern, is the Fourier transform matrix and is the cth coil-sensitivity diagonal matrix, pre-computed from fully sampled k-space using the E-SPIRiT algorithm [34].
A. Reconstruction using Blind Dictionary Learning
Like most model-based regularized reconstruction approaches, the blind sparsifying dictionary learning-based reconstruction scheme solves for an image x that is consistent with acquired measurements, and possesses properties that are ascribed to the image (or a class of images). Mathematically, the approach optimizes a cost function that balances a data-fidelity term and a data-driven sparsity inspired regularization term as follows [35]:
| (1) |
where ν > 0 reflects confidence in data fidelity and is a regularizer that, in the case of synthesis dictionary-based regularization, reflects the presumed sparsity of image patches as follows:
| (2) |
where extracts the jth overlapping patch of an image as a vector, denotes an overcomplete dicitionary, du its uth atom, ej the sparse codes for the jth patch and the jth column of Z, and λ is the sparsity penalty weight for dictionary learning, respectively.
A typical approach to solving this blind dictionary learning reconstruction problem is to alternate between updating the dictionary and sparse representation in (2) using the current estimate of the image x, called dictionary learning, and then updating the reconstructed image itself (image update) through (1) using the current estimate of the regularizer parameters [36]. This alternation between dictionary learning and image update is repeated several times to obtain a clean reconstruction. Let Bi(·) denote the function representing the ith iteration of this algorithm, and be the reconstructed image at the start of the iteration, then we have
| (3) |
where νi λi denote regularization parameters at the ith iteration for data fidelity and for dictionary learning, respectively. After K iterations, we have,
| (4) |
where represents the composition of F functions fF ∘ fF–1∘ … ∘f1, and x0 is an initial image, possibly a zero-filled reconstruction.
In this work, we used a few iterations of the SOUP-DIL algorithm [36] for the dictionary and sparse representation update (or dictionary learning) in (2) and the conjugate gradient method for the image update step. (See next section for details.) We also denote blind learning reconstruction as B in several figures and tables in subsequent sections.
In our comparisons, we also investigated a similar iterative scheme as in (3), but the dictionary D in (2) is not learned from data, and is instead fixed (e.g., to a discrete cosine transform (DCT) or wavelet basis).
B. Reconstruction using Supervised Learning
The supervised learning module (MoDL [20]) also aims to solve (1). Introducing an auxiliary variable z, (1) becomes:
| (5) |
where μ controls the consistency penalty between x and z. MODL updates x and z in alternation. The z update is:
| (6) |
We replace the proximal operator in (6) with a residually connected denoiser Dθ + I applied to xl, where I is the identity mapping.
The x update involves a regularized least-squares minimization problem:
| (7) |
solved via conjugate gradient method.
Similar to blind learning, the lth iteration of supervised residual learning-based reconstruction algorithm can be written:
| (8) |
where denotes the input image for the residual learning-based reconstruction algorithm. After L iterations, we have
| (9) |
The network parameters θ are learned in a supervised manner so that xsupervised matches known ground truths (e.g., in mean squared error or other metrics) on a training data set. We also denote supervised learning reconstruction as S in several figures and tables in subsequent sections.
C. Combining Blind and Supervised Reconstruction
Fig. 1 (P1) depicts our proposed BLIPS approach to combining blind and supervised learning. The skipped connection in the deep network enables the addition of the previous iterate to the output of the denoiser during supervised reconstruction, and ensures separation (the output of the residual denoiser gets added to the blind image going into data consistency) of the blind learned image and the supervised learned image in the first iteration when the aforementioned algorithms are combined. In subsequent iterations, this skipped connection also causes the denoiser to learn residual features after the combination of blind and supervised learning in the previous iteration. The output of the full pipeline of our proposed method Fig. 1 (P1) is:
| (10) |
Fig. 1.
Proposed pipelines (P1), (P2) and (P3) for combining blind and supervised learning-based MR image reconstruction.
We also refer to this pipeline as B+S in subsequent sections and figures.
D. Training the Denoiser Network
The denoiser Dθ shares weights across iterations. To train it, we use the output of our proposed pipeline (P1) in a combined ℓ1 and ℓ2 norm training loss function as follows:
where n indexes the training data consisting of target images reconstructed from fully sampled measurements and corresponding undersampled k-space measurements, and denotes the training loss function. The initial are obtained from the undersampled k-space measurements using a simple analytical reconstruction such as zerofilling inverse FFT reconstruction. Our implementation used β = 0.01 in (11), which was chosen empirically.
E. Direct Addition of Blind and Supervised Learning
A special case we investigate is when there is no residual connection in (P1), and we add the blind reconstruction output directly to the output of the supervised deep network during the data consistency update, as described in (11) below. Similar to (P1), the input to the supervised module is also the blind reconstruction output. We express an iteration of such an algorithm as follows:
| (11) |
where x0 = x′ is the initial input to the supervised module. After L iterations, the reconstruction is:
| (12) |
where , as depicted in Fig. 1 (P2). The training loss for this variation is:
| (13) |
F. Combined Supervised and Blind Learning with Feedback
Since iterations of blind learning-based reconstruction take significantly longer than propagating an image through a deep network, we investigated a feedback-based pipeline that reduces computation by only approximately optimizing the objective of blind learning reconstruction (using an outer single iteration of the blind learning module) that in turn is warm-started by a supervised learning reconstruction. The result of partial blind learning is then fed into a second stage with a supervised deep network similar to (P1), as depicted in Fig. 1 (P3), introducing image-adaptive features that may improve image quality. Essentially, the output for this pipeline can be expressed as:
| (14) |
where θ1 and θ2 are the weights of the initial and second stage unrolled networks, respectively. The training losses for these unrolled networks are:
| (15) |
| (16) |
respectively, where and the other symbols are as explained above. We train θ1 and θ2 separately in two stages. The training of θ2 starts after θ1 converges. The combination of supervised and partial blind learning could be iterated. We worked with a two-stage network architecture and a single iteration of blind learning optimization to keep computations low. In subsequent sections and figures, we also refer to this pipeline as S+B+S.
III. Experimental Framework
A. Training and Test Dataset
We trained and tested both our method and a strict supervised learning-based method with the same deep learning architecture (described below) on two datasets1. The first was a randomly selected subset from the fastMRI knee dataset, while the second consisted of the entire fastMRI brain dataset [29]. In the first case, our dataset for training and testing consisted of 8705 knee images, and were used in experiments involving the proposed pipelines in (P1) and (P2). We used smaller and randomly-selected subsets for our various experiments, which is described in detail in section IV.
To test the pipeline proposed in (P3), we used the fastMRI Brain dataset, consisting of 23220 T1 weighted images, 42250 T2 weighted images and 5787 FLAIR slices. For each contrast, we reserved 500 images as the test data and the rest for training and validation.
All sensitivity maps were estimated using the ESPIRiT [34] method. The details of the algorithms in our work are explained below.
B. Undersampling Masks
For experiments with the pipeline (P1), we used three types of undersampling masks. First, we used the 5× Cartesian phase encode undersampling mask shown in Fig. 2(a) that was held fixed across training and test images. This pattern had 29 fully sampled lines in the center of the k-space, and the remaining lines were sampled uniformly at random. We similarly tested (P1) on 2D Poisson-disk Cartesian undersampling at 20× acceleration. Finally, we tested (P1) by varying the 1D phase encode undersampling mask Fig. 2(a) used across training and test images randomly, to further evaluate its generalizability across different sampling patterns. For this purpose, we used ≈ 4.5× undersampling, and 24 fully sampled k-space lines. Pipeline (P2) was tested using only the sampling pattern in Fig. 2(a), while (P3) was tested using 8× equidistant acceleration mask shown in Fig. 2(c), as well as the 1D phase encode mask in Fig. 2(a). This mask had 4% fully sampled lines at the center of k-space [29].
Fig. 2.

Undersampling masks used in experiments: (a) 5-fold undersampled 1D Cartesian phase-encoded; (b) 20-fold undersampled Cartesian Poisson-disk; and (c) 8-fold equidistant.
C. Blind Dictionary Learning-based Reconstruction
We used the SOUP-DIL algorithm [36] to perform blind dictionary learning-based reconstruction initialized with a ‘zero-filled’ reconstruction of the data. In both (P1) and (P2), we set the number of outer iterations to be K = 20, and each outer iteration had 5 inner iterations of dictionary learning and sparse-coding. We set νi = 8 × 10−4 and λi = 0.2 across iterations, respectively. The dictionary size was 36 × 144 and the initial dictionary was an overcomplete inverse DCT matrix, while the sparse code matrix was initialized with zeros. We used conjugate gradient method to perform the data consistent image update. It required ≈ 170 seconds to perform 20 iterations of SOUP-DIL reconstruction of a single 640 × 368 image slice, on an Intel(R) Xeon(R) E5-2698 with 40 cores. For (P3), we used only one (K = 1) iteration of SOUP-DIL reconstruction with ν = 0.5 and λ = 0.8 on the fastMRI brain dataset (when used on the knee dataset, these were fixed to values mentioned earlier). For experiments involving the fastMRI brain dataset and pipeline (P1), we only use K = 3 outer iterations of SOUP-DIL reconstruction, due to the huge dataset size. A single iteration of SOUP-DIL took ≈ 6.5 seconds to reconstruct a 640 × 320 image on the same server. (Table VIII in the Supplementary Materials compares reconstruction time for different methods.)
When performing non-adaptive dictionary-based reconstruction, we fixed the dictionary to its inverse DCT initialization across all iterations, while keeping all other algorithm parameters unchanged. The experiment and results are shown in Sec. VII-A of Supplementary Materials.
An additional experiment compared the compressed sensing algorithm against blind dictionary learning. We used the MRI reconstruction instance included in the SigPy package2, which uses the primal-dual hybrid gradient (PDHG) algorithm and 30 iterations. The sparsity penalty is the ℓ1 norm of a orthogonal discrete wavelet transform, with a weight of 10−7 compared with the data-fidelity term.
D. Supervised Reconstruction
The denoiser Dθ we used is the Deep Iterative Down-Up Network [37], which has been shown to be efficient on previous benchmark research with the same fastMRI dataset [18] and in an image denoising competition [38]. Real and imaginary component of the complex-valued images are formulated as two input channels of the network. The magnitude of the input image is normalized by the median absolute value. The batch size is set to 4. We set the data-fidelity weight ν = 2 for the supervised learning.
In each iteration of (8), we used the conjugate gradient method to solve the least-squares minimization problem. Back-propagation of the least-squares problem (calculation of the Jacobian-vector product) is also performed using the conjugate gradient method. Here we set L = 6 to balance reconstruction quality and model dimension. In the inference phase, the time cost is around 1.2s for a 20-channel 640 × 320 slice on a single Nvidia(R) GTX1080Ti GPU. For a fair comparison, the denoiser training settings are the same between different scenarios in Section IV. The number of epochs is set to 40, with a linearly decaying learning rate from 1e-4 to 0. The optimizer was Adam [39], with parameter βs = [0.5,0.999].
E. Performance Metrics
For a quantitative comparison of the reconstruction quality, we used three common metrics: peak signal-to-noise ratio (PSNR, in dB), structural similarity index (SSIM) [40], and high-frequency error norm (HFEN) [12], to measure the similarity between reconstructions and ground truth. The HFEN was computed as the ℓ2 norm of the difference of edges between the input and reference images. Laplacian of Gaussian (LoG) filter was used as the edge detector. The kernel size was set to 15 × 15, with a standard deviation of 1.5 pixels.
IV. Results
A. Comparing Blind+Supervised vs Strictly Supervised Reconstruction
Table I compares the performance of combined blind and supervised learning versus strictly supervised learning on datasets of various sizes using (P1). We used 4 training dataset sizes: 1105, 2244, 4198, and 8205 slices. 10% for each training set was reserved for validation purposes. The test set consisted of 500 different slices. Training/validation set and test set are from different subjects to avoid data leakage between slices.
Table I:
Comparison of supervised learning-based reconstruction (S) versus our proposed combined blind and supervised learning-based reconstruction (B+S) using (P1) at various knee training dataset sizes for 5× acceleration using 1D Cartesian undersampling. The undersampling mask in Fig. 2a was held fixed for training and testing. Bold digits indicate that B+S method performed significantly better than the S method under pairwise t-test (P < 0.005).
| Dataset Size | 8205 | 4198 | 2244 | 1105 | ||||
|---|---|---|---|---|---|---|---|---|
| Method | S | B+S | S | B+S | S | B+S | S | B+S |
| SSIM | 0.944 | 0.947 | 0.942 | 0.946 | 0.939 | 0.943 | 0.930 | 0.941 |
| PSNR (dB) | 35.44 | 35.70 | 35.09 | 35.53 | 34.65 | 35.05 | 33.92 | 34.82 |
| HFEN | 0.450 | 0.433 | 0.470 | 0.443 | 0.494 | 0.471 | 0.538 | 0.484 |
Our proposed method’s improvements are fairly robust even when the total dataset size increases, as illustrated in Fig. 3 that depicts Table I as a bar chart. Moreover, for small-scale datasets, which are usually the case in medical imaging, our method still provides significant improvements over the strict supervised scheme. We conjecture that the blind learning-based reconstruction provides an image where many artifacts have been resolved and details have been restored that the supervised learning reconstruction can further refine.
Fig. 3.
Comparison of strict supervised learning-based reconstruction with BLIPS reconstruction across various knee dataset sizes. Table I shows the corresponding quantitative values.
Tables II and III display the quantitative results with the 2D Poisson disk Cartesian sampling pattern and 1D variable density Cartesian sampling mask (changing randomly across training and test cases), respectively. The training/validation set consisted of 4198 slices and the test set consisted of 500 slices (same as the 4198/500 slices in the previous case). The improvement provided by our scheme (B+S) over strict supervised learning (S) holds for multiple sampling masks, and is significant under the paired t-test (P < 0.005).
Table II:
Comparison of supervised learning-based reconstruction versus our proposed BLIPS and blind learning-based reconstruction using (P1) for 20 × acceleration using Cartesian 2D Poisson disk undersampling with mask shown in Fig. 2b. The fastMRI knee dataset was used for training and testing. Bold digits indicate that B+S method performed significantly better than the S method under paired t-test (P < 0.005).
| Recon. Method | Supervised | Blind | Blind+Supervised |
|---|---|---|---|
| SSIM | 0.960 | 0.949 | 0.963 |
| PSNR (dB) | 35.33 | 33.38 | 35.81 |
| HFEN | 0.434 | 0.507 | 0.403 |
Table III:
Comparison of performance of supervised learning-based reconstruction against our proposed BLIPS and blind learning-based reconstruction using (P1) for ≈ 4.5× acceleration using random variable density 1D sampling mask (changing randomly across training and test cases). The fastMRI knee dataset was used for training and testing. Bold digits indicate that B+S method performed significantly better than the S method under paired t-test (P < 0.005).
| Recon. Method | Supervised | Blind | Blind+Supervised |
|---|---|---|---|
| SSIM | 0.954 | 0.945 | 0.957 |
| PSNR (dB) | 34.34 | 32.79 | 34.80 |
| HFEN | 0.308 | 0.360 | 0.284 |
To support the assertion that BLIPS can learn different features than supervised learning, Figs. 4, 5, and 6 also display example slices. Compared to supervised learning, the most obvious difference in the combined model is the better restoration of fine details. It can be seen that in the blind dictionary learning results, a fair amount of fine structure is already recovered from the aliasing artifacts. The dictionary learning results provide a foundation for supervised learning to then residually reduce aliasing artifacts while preserving these details. This is also strongly implied by our observations in Section VII B and accompanying Fig. 9.
Fig. 4.
Comparison of reconstructions for a knee image using the proposed method versus strict supervised learning, blind dictionary learning, and zero-filled reconstruction for the 5× undersampling mask depicted in Fig. 2a. Metrics listed below each reconstruction correspond to PSNR/SSIM/HFEN respectively. The inset panel on the bottom left in each image corresponds to regions of interest (indicated by the red bounding box in the image) in the image that benefits significantly from BLIPS reconstruction, while the inset on the bottom right depicts the corresponding error map.
Fig. 5.
Comparison of reconstructions of a knee image using the proposed method versus strict supervised learning, blind dictionary learning, and zero-filled reconstruction for the 20× Poisson-disk undersampling mask depicted in Fig. 2b. Metrics listed below each reconstruction correspond to PSNR/SSIM/HFEN respectively. The inset panel on the bottom left in each image corresponds to regions of interest (indicated by the red bounding box in the image) in the image that benefits significantly from BLIPS reconstruction, while the inset on the bottom right depicts the corresponding error map.
Fig. 6.
Comparison of reconstructions of a knee image using the proposed method versus strict supervised learning, blind dictionary learning, and zero-filled reconstruction for the random 1D undersampling masks (≈4.5×). Metrics listed below each reconstruction correspond to PSNR/SSIM/HFEN respectively. The inset panel on the bottom left in each image corresponds to regions of interest (indicated by the red bounding box in the image) in the image that benefits significantly from BLIPS reconstruction, while the inset on the bottom right depicts the corresponding error map.
Table IV compares the proposed BLIPS techniques to strict supervised learning, and to supervised learning initialized with compressed sensing. The compared methods were trained and tested on identical datasets (4198 slices). The results indicate that the S+B+S BLIPS reconstruction yields the best performance, and the B+S reconstruction provides the second best performance. However, even compressed sensing reconstruction combined with supervised learning-based reconstruction performs better than strict supervised learning-based reconstruction.
Table IV:
Comparison of supervised learning-based reconstruction versus various proposed BLIPS reconstruction approaches using (P1) and (P2), and CS-initialized supervised reconstruction for 5× acceleration using 1D Cartesian undersampling with mask shown in Fig. 2a. Training was performed using 4198 knee slices from the fastMRI Knee dataset. Bold digits indicate that S+B+S method performed significantly better than the S method and CS+S method under paired t-test (P < 0.005).
| Recon. Method | S | B | CS+S | B+S | S+B+S |
|---|---|---|---|---|---|
| SSIM | 0.942 | 0.906 | 0.943 | 0.946 | 0.948 |
| PSNR (dB) | 35.09 | 30.29 | 35.24 | 35.53 | 35.83 |
| HFEN | 0.470 | 0.648 | 0.464 | 0.443 | 0.426 |
B. Strict Separation of Blind and Supervised Learning Reconstruction
Table V compares explicitly combining blind and supervised learning using (P2) without residual learning against the proposed method for combining blind and supervised learning. The sampling pattern here is the same as in Fig. 2a. The dataset is the same as the 8205/500 case in Table I. Compared to explicit consistency with blind learning results, our latent approach reaches a better result. The results demonstrate that rather than a fidelity prior, the blind learned reconstruction works better as an input to the deep residual network for further refinement.
Table V:
Comparison of combined blind and supervised learning using (P1) versus explicit addition of blind and supervised learning using (P2) for the mask in Fig. 2a. Training was performed using 4198 knee slices from the fastMRI Knee dataset. Bold digits indicate that B+S method performed significantly better than the explicit blind + supervised method under paired t-test (P < 0.005).
| Recon. Method | Explicit Blind + Supervised |
Proposed Blind + Supervised |
|---|---|---|
| SSIM | 0.938 | 0.946 |
| PSNR (dB) | 34.29 | 35.53 |
| HFEN | 0.495 | 0.443 |
C. Combined Supervised and Blind Learning with Feedback
For the large-scale brain dataset, we tested the idea of using a supervised learning network’s output as a potentially improved initialization for blind learning (14). The blind learning cost is then optimized for a single iteration with this improved initialization to incorporate additional details captured with blind learning to improve the first supervised network’s reconstruction. The blind learning result is passed on to another (second) stage of supervised learning. The networks’ parameters θ1 and θ2 are pre-trained on all three contrasts and fine-tuned on individual contrast, including T1w, T2w and FLAIR. As a control method, we concatenated two supervised learned networks sequentially, which can also improve the reconstruction performance compared with a single unrolled supervised network, and demonstrates substantial improvements in PSNR, SSIM, and HFEN for S+B+S with a large dataset. We also compare to deep supervised reconstruction preceded by a few iterations of blind dictionary learning. (We used 3 iterations here due to the time constraints associated with generating data for the large fastMRI brain dataset.)
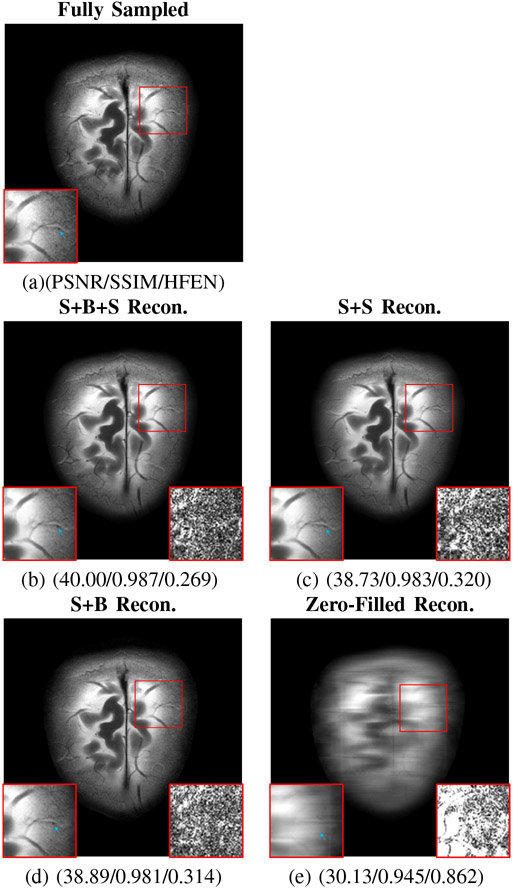
Table VI summarizes the results of this comparison, showing that while S+B+S performs the best, even B+S (which on the brain dataset, only used 3 iterations of SOUP-DIL reconstruction in the blind module) manages to outperform strict supervised learning in most contrasts. Fig. 7 shows an example slice for this comparison. Again, combined blind and supervised learning using (P3) preserves finer details better than cascaded strict supervised learning. Since our proposed method is dubbed blind primed supervised learning, in this comparison S+B+S is considered to be the BLIPS reconstruction, and S+B is the dictionary learning initialization.
Table VI:
Comparison of strictly supervised learning-based reconstruction (S+S) versus the proposed combined blind and supervised learning-based reconstruction (S+B+S) in (P3) for the fastMRI brain dataset with 8× undersampling with the mask in Fig. 2c
| Dataset | T1w | T2w | FLAIR | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Method | S+S | B+S | S+B+S | S+S | B+S | S+B+S | S+S | B+S | S+B+S |
| SSIM | 0.965 | 0.966 | 0.968 | 0.964 | 0.966 | 0.967 | 0.944 | 0.945 | 0.947 |
| PSNR (dB) | 36.86 | 36.85 | 37.27 | 35.37 | 35.72 | 35.88 | 34.23 | 34.36 | 34.62 |
| HFEN | 0.388 | 0.384 | 0.369 | 0.371 | 0.353 | 0.349 | 0.481 | 0.470 | 0.458 |
Fig. 7.
Comparison of reconstructions for two T2w brain images using the S+B+S learning reconstruction method proposed in (P3) versus cascaded S+S strict supervised learning-based reconstruction, S+B reconstruction, and zero-filled reconstruction for an 8× equidistant undersampling mask. The S+B reconstruction depicts the output of one iteration of blind reconstruction initialized with a supervised reconstruction. Metrics listed below each reconstruction correspond to PSNR/SSIM/HFEN respectively.The inset panel on the bottom left in each image corresponds to regions of interest (indicated by the red bounding box in the image) in the image that benefits significantly from BLIPS reconstruction, while the inset on the bottom right depicts the corresponding error map. The blue arrows indicate the position of image detail that is present in the the BLIPS reconstruction, but not strict supervised learning-based reconstruction.
D. Performance in the Presence of Planted Features
To compare the ability of BLIPS reconstruction and strictly supervised reconstruction to faithfully reproduce image features that are not present in the training dataset (as is often the case with identifying pathologies, etc.), we planted some features in a knee image from the fastMRI dataset, from which raw k-space was simulated and undersampled, inspired by [28]. The undersampling pattern was 1D variable density ≈ 4.5×, and was chosen at random to further test robustness.
Fig. 8 shows the aforementioned comparison. The BLIPS reconstruction reproduces the planted features with significantly higher fidelity than strict supervised reconstruction, and has much fewer aliasing artifacts, as is evident from the residue maps (also pointed out by the blue arrows in the figure). The details or edges of the planted features are better preserved in the BLIPS reconstruction compared to strict supervised learning-based reconstruction. The phenomena are consistent across simulated attempts we have tried.
Fig. 8.
Comparison of reconstructions of a knee image using the proposed method versus strict supervised learning for an image slice with artificially planted features. The undersampling mask was chosen to be random ≈4.5×. Metrics listed below each reconstruction correspond to PSNR/SSIM/HFEN respectively. The inset panels on the bottom in each image correspond to regions of interest (indicated by the red/green bounding boxes in the image) in the image that benefit significantly from BLIPS reconstruction, while the insets on the top depicts the corresponding error map. The blue arrows indicate the position of an aliasing artifact that is present in the zero-filled reconstruction and strict supervised learning, but not in the BLIPS reconstruction.
V. Discussion
This work investigated the combination of blind and supervised learning algorithms for MR image reconstruction. Specifically, we proposed a method that combines dictionary learning-based blind reconstruction with model-based supervised deep reconstruction in a residual fashion. Considering both S+B+S and B+S reconstruction under the same umbrella of BLIPS methods, comparisons against strictly supervised learning-based reconstruction indicate that the proposed reconstruction method significantly improves reconstruction quality in terms of metrics including PSNR, SSIM, and HFEN, across a range of undersampling and acceleration factors. The robustness of these improvements to the training dataset size suggests that the features learned during blind learning-based reconstruction using a sparse dictionary adapted separately for each training and testing image may differ significantly from features learned by deep networks trained on a large dataset with strictly pixel-wise supervision. While the latter showcases the potential for removing global aliasing artifacts, the former successfully leverages patterns in an image that are learned just from its measurements, thereby preserving the finer details of the image in the reconstruction. This claim is further supported by the error maps of regions of interest of reconstructed image slices. Moreover, the experiments using planted features suggest that BLIPS reconstruction can adapt to, and reproduce unfamiliar (absent from the training set) features better than strict supervised learning-based reconstruction. This ability may be a distinct benefit in the context of identifying pathology in MRI images. The combination of compressed sensing MRI and deep-supervised learning-based reconstruction also outperformed strict supervised learning-based reconstruction, reinforcing that features learned using supervision may not subsume traditional sparsity-based priors.
Past studies have shown that deep learning-based reconstruction is good at reducing aliasing artifacts compared with model-based iterative methods such as compressed sensing. The majority of supervised models are trained with pixel-wise ℓ1/ℓ2 norm loss. These approaches generally produce smooth images with high PSNR but can also introduce blurring. Other methods use GANs or perceptual loss to preserve details. However, these data-driven methods are often known to introduce realistic artifacts, which is very risky for medical imaging reconstruction. In our approach, the intrinsic sparsity of MR images is exploited in the dictionary learning phase to preserve fine structures. Thus, our method combines the advantages of both worlds: the representation ability of CNNs to resolve aliasing artifacts and dictionary-based signal modeling to recover high-frequency details. The superior performance in fine-detail recovery is reflected in the smaller HFEN values that quantify high-frequency features.
From the network training perspective, compared to the pure supervised model our network demonstrates improved stability and generalizability since it is powered and complemented by both model-based and adaptive dictionary learning-based components. First, on a relatively small dataset (1105/2244 images), the method still achieved similar results as with the full (8205 images) training dataset. This means that our method has clearly lower requirements on the amount of training data to work well compared to the massive amount of training data needed by typical deep learning-based reconstruction algorithms. Second, the improvements hold across different sampling patterns with very different PSFs. Third, although 40 training epochs were used in experiments, our approach requires only 5-8 epochs to converge (with no obvious overfitting seen thereafter). In contrast, the supervised model required 20-30 epochs for the training loss to converge.
Due to the serial nature of the SOUP-DIL algorithm [36] used for dictionary learning here, our algorithm’s reconstruction time is higher than that of strictly supervised reconstruction. The computational bottleneck is in the atom-wise block-coordinate descent approach to dictionary updating, which cannot be accelerated by simple vectorization. These alternating updates between each dictionary atom and the corresponding sparse codes [36] allow for the blind algorithm to residually learn and represent features in the reconstructed image. Further acceleration of the blind dictionary learning approach might be needed to use the approach in clinical settings that need a real-time imaging reconstruction workflow. However, it may be still acceptable for most conventional settings since the scanning itself is often the throughput bottleneck. The proposed S+B+S approach involves a much quicker (partial) dictionary learning-based step compared to the proposed vanilla B+S approach. Other fast blind learning approaches involving transform learning [12] could also make our schemes much more efficient.
VI. Conclusion and Future Work
This paper investigated a combination of shallow dictionary learning and deep supervised learning for MR image reconstruction that leverages the complementary nature of the two methods to bolster the quality of the reconstructed image. We verify this benefit by comparisons using a variety of metrics (including SSIM, PSNR, and HFEN) against strictly supervised learning-based reconstruction, reconstruction as initialization. We also investigate alternative approaches for combining the two forms of reconstruction. Our observations suggest that the primary benefits of including blind learning in the reconstruction pipeline are the preservation of ‘finer’ details in the output image and robustness to the availability of training data.
In the future, we aim to apply our methods to non-Cartesian undersampling patterns such as radial and spiral patterns, and to other modalities. The generalizability of the method, especially with heterogeneous datasets, will be further explored. We observed some variation in the performance of our method to the imposed sparsity level in (2). More careful tuning of hyperparameters will be necessary to optimize the overall performance of such methods. Curiously, we also observed that using additional iterations of blind learning reconstruction in (14) adversely impacted the performance of our methods. The cause for this behavior is unknown (beyond oversmoothing), and needs further investigation. We also plan to investigate the benefits of multiple iterations of combined blind and supervised learning based reconstruction, extending the S+B+S approach considered here. Aside from the benefits of traditional ‘handcrafted’ priors in combination with supervised deep learning, from the perspective of learning only from measurements of the image being reconstructed, and then filling in the gaps with supervised data-driven learning, it would be interesting to study the combination of deep blind approaches [41]-[44] with deep supervised learning.
Supplementary Material
Acknowledgments
This work was supported in part by NSF Grant IIS 1838179 and NIH Grant R01 EB023618.
Footnotes
Contributor Information
Anish Lahiri, Department of Electrical and Computer Engineering, University of Michigan, Ann Arbor, MI 48109, USA.
Guanhua Wang, Department of Biomedical Engineering, University of Michigan, Ann Arbor, MI 48109, USA.
Saiprasad Ravishankar, Department of Computational Mathematics, Science and Engineering and the Department of Biomedical Engineering, Michigan State University, East Lansing, MI 48824, USA.
Jeffrey A Fessler, Department of Electrical and Computer Engineering, University of Michigan, Ann Arbor, MI 48109, USA.
REFERENCES
- [1].Lustig M, Donoho D, and Pauly JM, “Sparse MRI: The application of compressed sensing for rapid MR imaging,” Magn. Reson. Med, vol. 58, no. 6, pp. 1182–1195, December. 2007. [DOI] [PubMed] [Google Scholar]
- [2].Liu Y et al. , “Balanced sparse model for tight frames in compressed sensing magnetic resonance imaging,” PLOS ONE, vol. 10, no. 4, p. e0119584, March. 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Eksioglu EM, “Decoupled algorithm for MRI reconstruction using nonlocal block matching model: BM3D-MRI,” J. Math. Imaging Vision, vol. 56, no. 3, pp. 430–440, November. 2016. [Google Scholar]
- [4].Jacob M, Mani MP, and Ye JC, “Structured low-rank algorithms: Theory, magnetic resonance applications, and links to machine learning,” IEEE Sig. Process. Mag, vol. 37, no. 1, pp. 54–68, February. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Candes EJ, Eldar YC, Needell D, and Randall P, “Compressed sensing with coherent and redundant dictionaries,” Appl. Comput. Harmon. Anal, vol. 31, no. 1, pp. 59–73, 2011. [Google Scholar]
- [6].Wen B, Li Y, and Bresler Y, “Image recovery via transform learning and low-rank modeling: The power of complementary regularizers,” IEEE Trans. Image Proc, vol. 29, pp. 5310–5323, 2020. [DOI] [PubMed] [Google Scholar]
- [7].Pratt WK, Andrews HC, and Kane J, “Hadamard transform image coding,” Proc. of the IEEE, vol. 57, no. 1, pp. 58–68, 1969. [Google Scholar]
- [8].Elad M, Milanfar P, and Rubinstein R, “Analysis versus synthesis in signal priors,” Inverse Probl, vol. 23, no. 3, p. 947, 2007. [Google Scholar]
- [9].Kobler E, Effland A, Kunisch K, and Pock T, “Total deep variation: A stable regularizer for inverse problems,” arXiv preprint arXiv:2006.08789, 2020. [DOI] [PubMed] [Google Scholar]
- [10].Roth S and Black MJ, “Fields of experts: A framework for learning image priors,” in 2005 IEEE Comp. Soc. Conf. on Comp. Vis. and Pat. Recogn. (CVPR’05), vol. 2. IEEE, 2005, pp. 860–867. [Google Scholar]
- [11].Ravishankar S and Bresler Y, “MR image reconstruction from highly undersampled k-space data by dictionary learning,” IEEE Trans. Med. Imaging, vol. 30, no. 5, pp. 1028–1041, May 2011. [DOI] [PubMed] [Google Scholar]
- [12].Ravishankar S and Bresler Y, “Learning sparsifying transforms,” IEEE Trans. Signal Process, vol. 61, no. 5, pp. 1072–1086, 2012. [Google Scholar]
- [13].Ravishankar S and Bresler Y, “Data-driven learning of a union of sparsifying transforms model for blind compressed sensing,” IEEE Trans. Comput. Imaging, vol. 2, no. 3, pp. 294–309, September. 2016. [Google Scholar]
- [14].Caballero J, Rueckert D, and Hajnal JV, “Dictionary learning and time sparsity in dynamic MRI,” in Int. Conf. on Med. Image Comput. and Comp.-Assist. Interv. (MICCAI 2012). Springer, 2012, pp. 256–263. [DOI] [PubMed] [Google Scholar]
- [15].Weller D, “Reconstruction with dictionary learning for accelerated parallel magnetic resonance imaging,” in Proc. of the IEEE Southwest Symp. on Image Anal. and Interp., vol. 2016-April. Institute of Electrical and Electronics Engineers Inc., April. 2016, pp. 105–108. [Google Scholar]
- [16].Lingala SG and Jacob M, “Blind compressive sensing dynamic MRI,” IEEE Trans. Med. Imaging, vol. 32, no. 6, pp. 1132–1145, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Gleichman S and Eldar YC, “Blind compressed sensing,” IEEE Trans. Inf. Theory, vol. 57, no. 10, pp. 6958–6975, 2011. [Google Scholar]
- [18].Schlemper J, Qin C, Duan J, Summers RM, and Hammernik K, “Sigma-net: Ensembled iterative deep neural networks for accelerated parallel MR image reconstruction,” arXiv preprint arXiv:1912.05480, 2019. [Google Scholar]
- [19].Ravishankar S, Lahiri A, Blocker C, and Fessler JA, “Deep dictionary-transform learning for image reconstruction,” in Proc.- 2018 IEEE 15th Int. Symp. on Biomed. Imag. (ISBI 2018), vol. 2018-April. IEEE Computer Society, May 2018, pp. 1208–1212. [Google Scholar]
- [20].Aggarwal HK, Mani MP, and Jacob M, “MoDL: Model-based deep learning architecture for inverse problems,” IEEE Trans. Med. Imaging, vol. 38, no. 2, pp. 394–405, February. 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Schlemper J, Caballero J, Hajnal JV, Price AN, and Rueckert D, “A deep cascade of convolutional neural networks for dynamic MR image reconstruction,” IEEE Trans. Med. Imaging, vol. 37, no. 2, pp. 491–503, February. 2018. [DOI] [PubMed] [Google Scholar]
- [22].Hammernik K et al. , “Learning a variational network for reconstruction of accelerated MRI data,” Magn. Reson. Med, vol. 79, no. 6, pp. 3055–3071, June. 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Yang G et al. , “DAGAN: Deep de-aliasing generative adversarial networks for fast compressed sensing MRI reconstruction,” IEEE Trans. Med. Imaging, vol. 37, no. 6, pp. 1310–1321, 2017. [DOI] [PubMed] [Google Scholar]
- [24].Eo T, Jun Y, Kim T, Jang J, Lee HJ, and Hwang D, “KIKI-net: Cross-domain convolutional neural networks for reconstructing undersampled magnetic resonance images,” Magn. Reson. Med, vol. 80, no. 5, pp. 2188–2201, November. 2018. [DOI] [PubMed] [Google Scholar]
- [25].Lee D, Yoo J, and Ye JC, “Deep residual learning for compressed sensing MRI,” in Proc.- 2017 IEEE 14th Int. Symp. on Biomed. Imag. (ISBI 2017). IEEE, 2017, pp. 15–18. [Google Scholar]
- [26].Mardani M et al. , “Deep generative adversarial neural networks for compressive sensing MRI,” IEEE Trans. on Med. Imaging, vol. 38, no. 1, pp. 167–179, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Ronneberger O, Fischer P, and Brox T, “U-net: Convolutional networks for biomedical image segmentation,” in Int. Conf. on Med. Image Comput. and Comp.-Assist. Intervent. (MICCAI 2015). Springer, 2015, pp. 234–241. [Google Scholar]
- [28].Antun V, Renna F, Poon C, Adcock B, and Hansen AC, “On instabilities of deep learning in image reconstruction and the potential costs of AI,” PNAS, vol. 117, no. 48, pp. 30 088–95, December. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Zbontar J et al. , “fastMRI: An open dataset and benchmarks for accelerated MRI,” arXiv preprint arXiv:1811.08839, 2018. [Google Scholar]
- [30].Van Essen DC et al. , “The WU-Minn human connectome project: An overview,” Neuroimage, vol. 80, pp. 62–79, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Quan TM, Nguyen-Duc T, and Jeong WK, “Compressed sensing MRI reconstruction using a generative adversarial network with a cyclic loss,” IEEE Trans. Med. Imaging, vol. 37, no. 6, pp. 1488–1497, June. 2018. [DOI] [PubMed] [Google Scholar]
- [32].Lei K, Mardani M, Pauly JM, and Vasanawala SS, “Wasserstein GANs for MR imaging: From paired to unpaired training,” IEEE Trans. Med. Imaging, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Ramzi Z, Ciuciu P, and Starck J-L, “XPDNet for MRI reconstruction: An application to the fastMRI 2020 brain challenge,” arXiv preprint arXiv:2010.07290, 2020. [Google Scholar]
- [34].Uecker M et al. , “ESPIRiT - An eigenvalue approach to auto-calibrating parallel MRI: where SENSE meets GRAPPA,” Mag. Reson. Med, vol. 71, no. 3, pp. 990–1001, March. 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Ravishankar S and Bresler Y, “MR image reconstruction from highly undersampled k-space data by dictionary learning,” IEEE Trans. Med. Imaging, vol. 30, no. 5, pp. 1028–1041, May 2011. [DOI] [PubMed] [Google Scholar]
- [36].Ravishankar S, Nadakuditi RR, and Fessler JA, “Efficient sum of outer products dictionary learning (SOUP-DIL) and its application to inverse problems,” IEEE Trans. Comput. Imaging, vol. 3, no. 4, pp. 694–709, April. 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Yu S, Park B, and Jeong J, “Deep iterative down-up CNN for image denoising,” in Proc. of the IEEE Conf. on Comp. Vis. and Pat. Recogn. (CVPR) Workshops, 2019, pp. 0–0. [Google Scholar]
- [38].Abdelhamed A, Timofte R, and Brown MS, “NTIRE 2019 challenge on real image denoising: Methods and results,” in Proc. of the IEEE Conf. on Comp. Vis. and Pat. Recogn. (CVPR) Workshops, 2019, pp. 0–0. [Google Scholar]
- [39].Kingma DP and Ba J, “Adam: A method for stochastic optimization,” arXiv preprint arXiv:1412.6980, 2014. [Google Scholar]
- [40].Wang Z, Bovik AC, Sheikh HR, and Simoncelli EP, “Image quality assessment: From error visibility to structural similarity,” IEEE Trans. Image Process, vol. 13, no. 4, pp. 600–612, 2004. [DOI] [PubMed] [Google Scholar]
- [41].Oh G, Sim B, Chung H, Sunwoo L, and Ye JC, “Unpaired deep learning for accelerated MRI using optimal transport driven CycleGAN,” IEEE Trans. Comput. Imaging, vol. 6, pp. 1285–1296, 2020. [Google Scholar]
- [42].Yaman B, Hosseini SAH, Moeller S, Ellermann J, Uğurbil K, and Akçakaya M, “Self-supervised learning of physics-guided reconstruction neural networks without fully sampled reference data,” Magn. Reson. Med, vol. 84, no. 6, pp. 3172–3191, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Tamir JI, Yu SX, and Lustig M, “Unsupervised deep basis pursuit: Learning inverse problems without ground-truth data,” arXiv preprint arXiv:1910.13110, 2019. [Google Scholar]
- [44].Ke Z, Cheng J, Ying L, Zheng H, Zhu Y, and Liang D, “An unsupervised deep learning method for multi-coil cine MRI,” Phys. Med. Biol, vol. 65, no. 23, p. 235041, 2020. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.