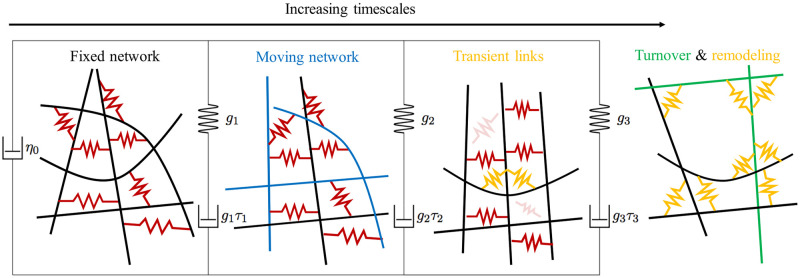
Fig 10. Our continuum model, informed by the timescales discussed in previous sections.

We use three Maxwell elements with timescales τ₁, τ₂, and τ₃, all in parallel with a viscous dashpot to describe the network. The viscous dashpot η₀ represents the high frequency viscosity of the permanently cross-linked fiber suspension. The first Maxwell element has timescale τ₁ ≈ 0.02 seconds associated with it, and represents the relaxation of the fibers to a transient elastic equilibrium (the networks before and after relaxation are shown to the left and right of this Maxwell element; the relaxing fibers are shown in blue); on this timescale, the links are effectively static. The second Maxwell element, with timescale τ₂ ≈ 0.5 s, represents the unbinding of some links (shown more transparent than the others) and the appearance of new links (orange) − compare the networks to the left and right of this Maxwell element. The third Maxwell element with timescale τ₃ ≈ 5 s represents network remodeling (compare the networks to the left and right of this element); for timescales larger than τ₃, some of the fibers (shown in green) and links (orange) turn over and the network completely remodels from the initial state.