ROAD: ROtational direct Aperture optimization with a Decoupled ring-collimator for FLASH radiotherapy

Abstract

Ultra-high dose rate in radiotherapy (FLASH) has been shown to increase the therapeutic index with markedly reduced normal tissue toxicity and the same or better tumor cell killing. The challenge to achieve FLASH using x-rays, besides developing a high output linac, is to intensity-modulate the high-dose-rate x-rays so that the biological gain is not offset by the lack of physical dose conformity. In this study, we develop the ROtational direct Aperture optimization with a Decoupled ring-collimator (ROAD) to achieve simultaneous ultrafast delivery and complex dose modulation. The ROAD design includes a fast-rotating slip-ring linac and a decoupled collimator-ring with 75 pre-shaped multi-leaf-collimator (MLC) modules. The ring-source rotates at 1 rotation per second (rps) clockwise while the ring-collimator is either static or rotating at 1 rps counterclockwise, achieving 75 (ROAD-75) or 150 (ROAD-150) equal-angular beams for one full arc. The Direct Aperture Optimization (DAO) for ROAD was formulated to include a least-square dose fidelity, an anisotropic total variation term, and a single segment term. The FLASH dose (FD) and FLASH biological equivalent dose (FBED) were computed voxelwise, with the latter using a spatiotemporal model accounting for radiolytic oxygen depletion. ROAD was compared with clinical volumetric modulated arc therapy (VMAT) on a brain, a lung, a prostate, and a head and neck cancer patient. The mean dose rate of ROAD-75 and ROAD-150 are 76.2 Gy s⁻¹ and 112 Gy s⁻¹ respectively to deliver 25 Gy single-fraction dose in 1 s. With improved PTV homogeneity, ROAD-150 reduced (max, mean) OAR physical dose by (4.8 Gy, 6.3 Gy). The average R50 and integral dose of (VMAT, ROAD-75, ROAD-150) are (4.8, 3.2, 3.2) and (89, 57, 56) Gy × Liter, respectively. The FD and FBED showed model dependent FLASH effects. The novel ROAD design achieves ultrafast dose delivery and improves physical dosimetry compared with clinical VMAT, providing a potentially viable engineering solution for x-ray FLASH radiotherapy.

1. Introduction

The improvement in physical radiation dose conformity via technological evolutions, including intensity-modulated radiotherapy (IMRT) (Brahme et al 1982, Bortfeld 2006), volumetric modulated arc therapy (VMAT) (Otto 2007, Palma et al 2010), and 4π non-coplanar radiation therapy (Dong et al 2013; Lyu et al 2018b; Yu et al 2018), will plateau. Particularly for normal tissues abutting the tumor, one must look beyond the physical dose for the next leap in the therapeutic ratio. Emerging evidence suggests that ultra-fast radiation delivery (dose rate > 40 Gy s⁻¹), termed FLASH radiotherapy, may lead to such a leap (Favaudon et al 2014a). Compared to conventional radiotherapy with dose rate ~0.1 Gy s⁻¹, FLASH radiotherapy markedly reduced the normal tissue toxicity without compromising tumor response (Bourhis et al 2019a, Favaudon et al 2014a, Vozenin et al 2019a, 2019b). The FLASH effects have been consistently observed across different animal species, including mice (Favaudon et al 2014a), cat (Vozenin et al 2019a), zebrafish (Beyreuther et al, 2019), and pig (Vozenin et al 2019a), in various tumor models including lung (Favaudon et al 2014a), breast (Favaudon et al 2014a), and brain (Favaudon et al 2014a, Montay-Gruel et al 2017, Simmons et al 2019), using different modalities including electron (Lempart et al 2019, Vozenin et al 2019a), x-ray (Montay-Gruel et al 2018), and proton (Beyreuther et al 2019). Moreover, the FLASH effect was recently demonstrated in a human study (Bourhis et al 2019b).

Nevertheless, there are significant technical challenges to achieving the ~500x greater dose rate for FLASH in human patients. The electron dose rates using existing linacs may be high enough, but the achievable energies are inadequate for most non-superficial tumors. Certain proton systems can be modified to achieve the high dose rate but only in the dosimetrically inferior transmissive mode, due to the non-negligible time required to switch between energy layers in the proton scanning spot mode.

Therefore, we are motivated to investigate an x-ray system for FLASH therapy with two essential components: a high output x-ray linac and the dose conformity comparable to state-of-the-art IMRT. It is believed that the high dose rate can be achieved with existing accelerator technology. Conventional medical linacs produce average electron beam powers of around 1 kW, while higher-power industrial and research accelerators routinely achieve powers on the order of 100 kW (Hamm and Hamm 2012). Assuming a dose conversion factor of 7.5 Gy s⁻¹ mA⁻¹ at 10 MeV(Schwartz 1978), the beam power needed to achieve 1 Gy s⁻¹ is 80 kW. Furthermore, we note that the ~100 kW industrial accelerators that are in operation around the world are designed to work continuously in a factory setting with very little downtime. In the case of FLASH, the beam will only be on for a brief time, on the order of 1 s, which significantly relaxes the requirements on, e.g. power supplies and cooling systems. While we do not claim that such an accelerator will be easy to produce, it is feasible with current technology.

Multiple beam angles and effective intensity modulation are necessary for good x-ray dose conformity. Existing delivery platforms are evidently incompatible with the FLASH requirement. To avoid the slow mechanical movements of the C-arm gantry and the multi-leaf collimator (MLC), Maxim et al (2019) proposed PHASER using high-intensity, pluridirectional MV x-ray beams and scanning electron pencil beams for IMRT. However, the success of PHASER depends on multiple groundbreaking technologies to be developed, adding significant uncertainties, a long development cycle, and high cost to the product.

Alternatively, to achieve ultrafast dose delivery and intensity modulation with x-rays, we propose to modify the existing method for delivering VMAT to enable FLASH delivery. We term the novel delivery method ROtational direct Aperture optimization with a Decoupled ring-collimator (ROAD), which employs a fast-rotating slip ring gantry, and a decoupled MLC-ring with many pre-shaped apertures for fast access to multiple beam entry angles and complex dose modulation.

2. Materials and methods

2.1. Hardware design of ROAD

The standard VMAT treatment delivers radiation continuously from a rotating gantry head that encloses a radiation source, jaws, and an MLC module (figure 1(A)). The MLC leaves move while the gantry rotates to form different aperture shapes at different beam angles. Due to the limited MLC leaf speed (typically <5 cm s⁻¹ at the isocenter distance), a constraint is imposed on the difference between adjacent apertures for practical VMAT delivery time. Reducing the delivery time to sub-second for FLASH would require faster source rotation and a different way to provide intensity modulation.

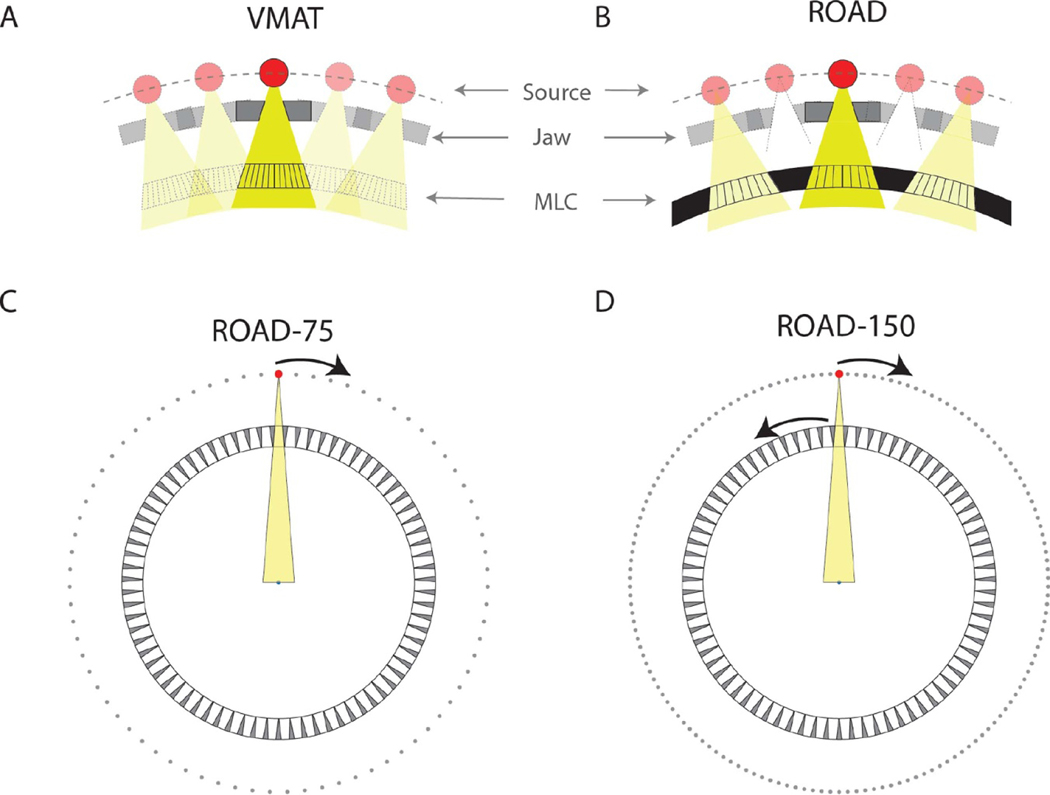
Figure 1.

(A) Demonstration of VMAT where the source, jaw, and MLC are aligned and rotate as a group. The radiation is delivered continuously throughout the entire treatment. The MLC leaf motion coordinates with the gantry rotation, forming different aperture shapes at different beam angles. (B) Zoomed-in demonstration of the hardware design of ROAD. The pulsed beam is triggered only when the fast-rotating source and jaw are aligned with one of the MLC openings. The MLC leaves in all openings are positioned prior to the treatment. (C) Assuming realistic physical parameters, the MLC-ring can fit 75 MLC modules with 15 cm beam width in the isocenter plane. With static MLC-ring, by rotating the source for one round, the source is sequentially aligned with all 75 MLC openings, achieving 75 beams within one rotation (ROAD-75). (D) By rotating the source and the ring-collimator in the opposite direction with the same speed, the source-MLC aligning positions are doubled, achieving 150 beams with one round of source rotation and collimator rotation (ROAD-150). A video demonstration of the ROAD-150 delivery can be found in the supplementary materials.

Figure 1(B) shows the proposed ROAD design. The fast-rotating source is achieved by mounting the linac on a slip-ring gantry with a speed of 1 rotation per second (rps). The linac, which is currently under development, has the following preliminary technical specifications: pulse length 83 μs, repetition rate 300 Hz, dose per pulse 2 Gy at the isocenter, energy 10 MV. To circumvent the mechanical limitations of a single MLC module, ROAD uses 75 MLC modules mounted on a separate ring that is either static or counter-rotating at 1 rps. Different from conventional VMAT, where the MLC leaves are always aligned with the x-ray target, in the decoupled configuration, the individual MLC modules are focused at 75 equally spaced points on the target ring. With an accurate measurement of the linac/MLC angles, the pulsed linac is triggered only when the target is aligned with one of the MLCs to eliminate the undesirable geometrical penumbra. Intensity modulation is then achieved by optimizing a single MLC aperture for each beam. Because apertures can be shaped before treatment, the MLC mechanical speed limitation is circumvented.

Figures 1(C) and (D) illustrate the ROAD design assuming the following physical and mechanical parameters. The source to isocenter distance (SID) is 100 cm, the distance between the MLC and the isocenter is 70 cm, the MLC thickness is 10 cm, and the beamlet resolution is 5 mm at the isocenter plane (the MLC physical width is 1.5 mm). A total of 75 identical MLC modules are installed on the ring-collimator, with 60 MLC leaves in each MLC module (30 leaves on each side). The beam field of view (FOV) is 15 cm in-plane and 20 cm cross-plane. The gantry rotation speed is 1 rps, and the MLC leaf traveling speed at the isocenter plane is 5 cm s⁻¹. With static ring-collimator in one full ring-source rotation, 75 equiangular beams can be utilized (ROAD-75) (figure 1(C)). By counter-rotating ring-collimator at 1 rps, 150 equiangular beams can be achieved (ROAD-150) (figure 1(D)). We assume a total delivery time of 1 s for both ROAD-75 and ROAD-150. In ROAD-150, the same MLC modules are used twice separated by 0.5 s, allowing up to 2.5 cm leaf motion at the isocenter plane in the transition to form new apertures. A video demonstration of the ROAD-150 delivery can be found in the supplementary materials.

2.2. Direct aperture optimization formulation

The direct aperture optimization for FLASH therapy is formulated as

$\begin{array}{c}\underset{f,c,u}{\text{minimize}}\underset{\text{fidelityterm}}{\frac{1}{2}{\Vert W\left((Af)-d_0\right)\Vert }_2^2}+\underset{\text{anisotropic}\text{TV term on}f}{\left({\lambda }_x{\Vert D_{x}f\Vert }_1+{\lambda }_y{\Vert D_{y}f\Vert }_1\right)}\\ +\underset{\text{single}\text{segment term}}{\frac{\gamma }{2}\left({\Vert \text{diag}{(u)}^{1/2}(f-c)\Vert }_2^2+{\Vert \text{diag}{(1-u)}^{1/2}f\Vert }_2^2\right)}\\ \text{subject}\text{to}0\le f\le I_{\max },0\le c\le I_{\max },u\in {\{0,1\}}^n,u\in S_d,\end{array}$ (1)

where f is the vectorized fluence map, c is the fluence intensity, and u is the vectorized aperture shape. U equals to 1 where the aperture exists, i.e. the beamlet is opened, and 0 elsewhere. The set S_d is defined to include all deliverable apertures. In the case of ROAD-150, the apertures in the set S_d are also required to satisfy the MLC speed constraint. I_max is the maximum intensity of the fluence map at each control point, which is limited by the maximum dose rate.

A is the fluence-to-dose transformation matrix, which converts the vectorized fluence map to the corresponding volumetric dose. W is the diagonal weighting matrix, where the diagonal elements are the weightings of the structures of interest. d₀ is the ideal dose with the prescription dose in the PTV and zero elsewhere. The least-squares fidelity term attempts to find the optimal fluence map f by penalizing the difference between the planning dose Af and the ideal dose d₀. In the second total variation (TV) term, D_x and D_y are the finite-difference matrices in the directions parallel and orthogonal to the MLC leaf motion, respectively. The anisotropic TV term encourages the piecewise continuity of fluence map f, and the amount of smoothness is controlled by λ_x and λ_y. The single segment term simplifies the final fluence map f to contain only a single segment at each control point. It pushes the fluence map f towards a uniform intensity value c within the aperture (u = 1, the beamlet is opened), and towards 0 outside the aperture (u = 0, the beamlet is closed). The single segment constraint is attained by gradually increasing the weighting parameter γ in the optimization.

2.3. Algorithm

The optimization problem in equation (1) was solved using an alternating optimization approach that has been investigated in our previous studies (Nguyen et al 2016, Lyu et al 2018a, 2018b, 2019). In each optimization iteration, the algorithm runs through three modules and optimizes with respect to each of the three optimization variables, c, and u, independently, holding the other two fixed. The process is repeated until f converges to $c\odot u$ (the elementwise/Hadamard product), indicating that single segment constraint is achieved. For ROAD-150, the optimization is initialized with the ROAD-75 plan generated using the same hyperparameters.

In the module optimizing with respect to the aperture u, the problem reduced to a graph optimization problem with a linear objective:

$\begin{array}{cc}\underset{{\left\{u_{\theta }\right\}}_{\theta =0}^n}{minimize}& \sum _{\theta }\langle q_{\theta },u_{\theta }\rangle ,\\ \text{subject}\text{to}& \begin{array}{l}{u}_{\theta }\in {\{0,1\}}^n,u\in S_d,\theta =1,2,\dots ,n_{\theta }\\ {\left(q_{\theta }\right)}_j={\left({\left(f_{\theta }\right)}_j-c_{\theta }\right)}^2-{\left(f_{\theta }\right)}_j^2\end{array}\end{array}$ (2)

where θ is the index for beam angle, and j is the index for elements in the corresponding vector. The minimization of the objective in equation (2) is equivalent to a simplified travelling salesman problem on a directed graph with a rectangular structure. To reduce the computation complexity, we first solved equation (2) without the constraint u ∈ S_d, and then project the resultant u^∗ to the feasible set S_d.

In the modules optimizing with respect to the fluence map f and the intensity c, the optimization problem was solved with the Fast Iterative Shrinkage-Thresholding Algorithm (FISTA) (Beck and Teboulle 2009). FISTA solves the optimization problem in the form of

$$\text{minimize}F(x)+G(x),$$ (3)

where F is a differentiable convex function with a Lipschitz continuous gradient, and G is a convex function of which the proximal operator (Parikh and Boyd 2013) can be evaluated efficiently. The optimization problem in equation (1) can be efficiently solved by FISTA by reformulating it into the canonical form shown in equation (3). Details on the algorithm can be found in appendix A1.

2.4. FLASH dose

When delivering a treatment plan, the physical dose changes both spatially and temporally. The spatial-dependency and time-dependency of delivered dose can be computed based on an existing treatment plan f(t_j) :

$$d_i\left(t_j\right)=A_i\cdot f\left(t_j\right),$$

where t_j is the time when the beam j was delivered, $f\left(t_j\right)$ is the fluence map of beam j, A_i is the dose matrix of voxel i, and $d_i\left(t_j\right)$ is the dose to voxel i at time t_j.

Similar to the physical dose, spatial and temporal variations also apply to the physical dose rate. The same physical dose could result in different FLASH effects, depending on the dose rate at each voxel. For example, if the majority of the dose delivered to a voxel was under a high dose rate, the FLASH effect within the voxel would be substantial. On the contrary, if the majority of the dose delivered to a voxel was under a low dose rate, the FLASH effect could be minimal. To evaluate the FLASH effect of the ROAD plan, the physical dose rate at each voxel needs to be evaluated at each time point.

We use the FLASH dose (FD) to denote a portion of the physical dose delivered under high dose rate, which could potentially achieve greater FLASH effect. The FD is defined as the cumulative physical dose delivered with an average dose rate higher than a threshold R for a minimum time interval of Δt (R = 40 Gy s⁻¹ and Δt=100 ms in this study). For voxel i, T_i is a set of time points with FD delivery:

$$T_i=\left\{t_s\mid \frac{{\sum }_{v=m}^n{d}_i\left(t_v\right)}{t_n-t_m}⩾R,t_n-t_m⩾\text{Δ}t,m⩽s⩽n,s,m,n\in {\mathbb{N}}^{+}\right\},$$

The FLASH dose at voxel i is defined as

$${\text{FD}}_i=\sum _{t_z\in T_i}{d}_i\left(t_s\right).$$

Under the same physical dose, a higher FD indicates less biological damage to the normal tissue.

2.5. FLASH biological equivalent dose

A quantitative biological model, the radiolytic oxygen depletion (ROD) model (Pratx and Kapp 2019), is adapted to evaluate the biological effect of the ROAD model. We assumed the same parameters as Pratx and Kapp (2019b) in this study.

The radioprotective effect of FLASH irradiation has been connected with decreased radiosensitivity of normal tissue cells due to transient ROD (Favaudon et al 2014a, Hendry et al 1982, Michaels 1986, Montay-Gruel et al 2019, Pratx and Kapp 2019a, 2019b, Spitz et al 2019, Vozenin et al 2019b). The effect of oxygen on radiosensitivity can be quantified according to the oxygen enhancement ratio (OER), defined as the ratio of the dose in anoxia to the dose under a certain oxygen tension p to achieve the same biological effect. One of the parameterizations of OER was proposed by Robert Grimes and Partridge (2015):

$$OER(p)=1+\alpha \left(1-e^{-\psi \cdot p}\right)$$

where α = 1.63, ψ = 0.26 mmHg⁻¹, and p is the transient oxygen tension.

To compute the transient oxygen tension in ROAD plan delivery, we devided the delivery process into two parts: within-pulse and between-pulse, and discuss them separately.

Within the high-intensity short-pulse (>10³ Gy s⁻¹), the effect of oxygen metabolism and tissue diffusion is negligible, and the transient oxygen tension has a linear relationship on the dose input (Weiss et al 1974, Michaels 1986):

$p_i^{+}=p_i^{-}-\text{L}\cdot d_i$ (4)

where i is the pulse index, d_i is the dose of pulse i, L is the ROD rate (0.42 mmHg Gy⁻¹) (Weiss et al 1974), $p_i^{-}$is the transient oxygen tension right before pulse i, and $p_i^{+}$ is the transient oxygen tension immediately after pulse i.

The oxygen tension $\left(p_i^{+}\to p_{i+1}^{-}\right)$ between the two dose-pulses (pulse i → pulse i + 1) changes with oxygen diffusion and tissue metabolisms. Following the computational model proposed by Pratx and Kapp (2019b), we assumed an infinitely long capillary (radius r₀ = 3 μm) and a constant oxygen tension within the capillary (p_cap = 40 mmHg). The effects of different capillary oxygen levels have been discussed in figure 6 in Pratx and Kapp (2019b). With polar symmetry, the oxygen diffusion and tissue metabolism is modeled in polar coordinates

$$\frac{\partial p}{\partial t}=\text{a}\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial p}{\partial r}\right)-\text{m,}$$ (5)

where the diffusion constant a = 2 10⁻⁵cm²s⁻¹ (Ferrell and Himmelblau 1967), oxygen metabolism rate m = 3 mmHgs⁻¹, and r is the distance of the cell from the capillary. The boundary condition is set by enforcing $p\left(r\le r_0\right)$= 40mmHg. Given the transient oxygen tension $p_i^{+}(r)$ right after pulse i, the transient oxygen tension $p_{i+1}^{-}(r)$ right before pulse i + 1 can be computed by solving equation (5) iteratively using a finite difference method (details can be found in appendix A2). The initial state p₀ (r) is set as the steady state of equation (5), which can be solved by setting$\frac{\partial p}{\partial t}=0$.

Figure 6.

Heat map of dose and FLASH dose distribution of normal tissue voxels receiving physical dose greater than 10 Gy, based on the ROAD-150 plans for all patients, assuming 25 Gy prescription dose in a single fraction. The heat map was normalized columnwise.

The transient oxygen tension p (t, r) in ROAD plan delivery can be computed voxelwise by iteratively applying equation (4) $\left(p_i^{-}\to p_i^{+}\right)$and solving equation (5) $\left(p_i^{+}\to p_{i+1}^{-}\right)$using the sequential dose pulses received by each voxel. A parallelization scheme to solve the partial differential equation efficiently for all voxels can be found in appendix A2.

In conventional VMAT plan delivery, the oxygen tension stays at the initial condition p₀ (r). We define the transient radiosensitivity S as the ratio of the transient dose in ROAD to the dose under conventional dose rate to achieve the same biological effect:

$$S(t)=\frac{OER(p(t))}{OER\left(p_0\right)}.$$

For simplicity, we assumed 75 μm from the capillary (r = 75 μm) for radiosensitivity evaluation. Figure 2 shows examples of the time series plots of the dose pulses and the transient radiosensitivity S, assuming different pulse sequences (pulse sequence 1–4) and the same total dose 25 Gy. Note that varying delivery time is assumed in this figure (from submillisecond to 15 s) to illustrate the different biological effects resulted from different delivery schemes. With an incident dose, transient oxygen tension drops, OER decreases, and subsequently, the transient radiosensitivity S falls off. Conversely, without irradiation, the radiosensitivity S gradually rebounds until it reaches 1. Under different dose patterns (pulse sequences 1–4), the transient oxygen tension p (t) could be different, leading to different transient radiosensitivity S, and different overall biological effects, even if the total dose is the same.

Figure 2.

(A) Time series plot of transient radiosensitivity S under different dose inputs (pulse sequences 1–4), assuming a total dose of 25 Gy. (B) Overall decrease in radiosensitivity as a function of the distance from capillary, plotted for all four pulse sequences. r = 75μm (indicated by the dashed line) were assumed for computing the transient radiosensitivity S in (A).

The fractional cell kill from an infinitesimal dose dD with a transient radiosensitivity S is

$$\frac{dN}{N}=\mu SdD,$$

where N is the number of surviving cells, and μ is a constant in units of Gy^–1. The FLASH biological equivalent dose (FBED) is defined as the dose to achieve the same biological effect in conventional dose rate irradiation, which is equivalent to the integral of the radiosensitivity over dose:

$$\text{FBED}=\int \text{Sd}D=\frac{\int OER(p(D))\text{d}D}{OER\left(p_0\right)}.$$

In general, the FLASH effect becomes more evident with increasing dose, due to an increased amount of oxygen depletion. In addition, the effect is also dependent on the dose sequence as illustrated in figure 2. This computational model evaluates the FBED individually for each voxel, based on the incident dose at each voxel level, as a comprehensive evaluation including both the total delivered dose and the dose sequences.

Note that the FBED calculation only applies to normal cells. We assumed the FBED of the PTV is equivalent to its physical dose for simplicity.

2.6. Evaluation

The single-arc ROAD plans were compared with clinical two-arc VMAT plans on four representative patients, including a glioblastoma multiforme case (GBM), a lung cancer case (LNG), a prostate cancer case (PRT), and a Head and Neck cancer case (H&N). The VMAT plans were planned on the Eclipse treatment planning system using two coplanar arcs with 90 ° collimator rotation. The dose matrix for ROAD was obtained using a convolution/superposition dose calculation algorithm with 10 MV x-ray polyenergetic kernels (Neylon et al 2014, Neph et al 2019). The gantry angles were sampled with 4.8 ° and 2.4 ° spacing for ROAD-75 and ROAD-150, respectively. For VMAT, the gantry angle was sampled with 2 ° spacing (180 control points in total). The beamlet size for dose calculation was 0.5 × 0.5 cm² for all plans. The beam FOV was 15 × 20 cm² for ROAD, and 20 × 20 cm² for VMAT. The dose voxel size was 0.25 × 0.25 × 0.25 cm³.

The dose rate was calculated by converting the machine output in Monitor Units (MU) to dose and dividing by the beam time:

$$\text{doserate}=\frac{\text{Output}(\text{MU})}{\text{time}(\text{s})}\times \frac{1(\text{Gy})}{100(\text{MU})}.$$

Conversion from fluence intensity to MU was calibrated by calculating unit-fluence dose in water using the same dose calculation algorithm and measuring the dose at dmax.

For ROAD plans, the physical dose, the FD, and the FBED were evaluated. The FD and FBED computation assumed 25 Gy prescription dose to the PTV in a single fraction. The physical dose of ROAD plans was compared with that of the corresponding clinical VMAT plans. The FD was computed for all normal-tissue voxels. The distribution of FD vs. physical dose was evaluated to show the potential FLASH effect of the ROAD plans. The FBED were computed following the biological model, assuming nominal parameter values and 25% uncertainty (p_cap = 40 ± 10 mmHg, L = 0.42 ± 0.105 mmHg Gy⁻¹, and a = 2 10⁻⁵ ± 5∙10⁻⁶cm²s⁻¹).

PTV statistics including PTV D98, D2, and PTV homogeneity (defined as$\frac{\text{D95}}{\text{D5}}$) were evaluated. R50, defined as the 50% isodose volume divided by the target volume, was also assessed to quantify the dose compactness. The integral dose was evaluated as total dose spillage. For OARs, the maximum dose (Dmax) and the mean dose (Dmean) were obtained. The maximum dose is defined as D2 (the dose at 2% of the structure volume), following the ICRU-83 report (Grégoire and Mackie 2011).

3. Results

3.1. Plan information

Table 1 reports the prescription doses, PTV volumes, single-fraction dose, estimated delivery time, and mean and maximal per-beam dose rate for all ROAD plans. The single fraction dose is assumed 2 Gy for VMAT and 25 Gy for the ROAD plans. For the H&N patient, the single fraction dose of the ROAD plan is 25 Gy for the partial PTV with the highest prescription dose (PTV70Gy) and scaled accordingly for the other PTV (PTV56Gy). On average, the mean dose rate of ROAD-75 and ROAD-150 are 76.2 Gy s⁻¹ and 112 Gy s⁻¹, respectively, and the maximal dose rate are 150 Gy s⁻¹ and 300 Gy s⁻¹. The maximal dose rate is limited by the optimization constraint that enforces a maximum of 2 Gy dose per control point. Note that the provided dose rate is amortized over the beam time, while the instantaneous dose rate (within-pulse dose rate) should be several orders higher, depending on the pulse duration. In addition, the instantaneous/maximal/mean dose rates are different from the dose rate distribution within the patient body, while the latter was used for voxelwise quantification of the FD and the FBED.

Table 1.

Prescription doses, PTV volumes, single-fraction dose, estimated delivery time per fraction, and mean and maximal per-beam dose rate for all plans.

Case	Method	Prescription dose (Gy)	PTV volume (cc)	Single-fraction dose (Gy)	Estimated delivery time (s)	Per-beam dose rate (Gy/s)
						Mean	Max
GBM	VMAT			2	132
	ROAD-75	25	6.359	25	1	94.66	150
	ROAD-150			25	1	141.25	300
LNG	VMAT			2	132
	ROAD-75	50	137.7	25	1	61.34	150
	ROAD-150			25	1	89.27	300
PRT	VMAT			2	132
	ROAD-75	40	84.17	25	1	71.64	150
	ROAD-150			25	1	111.84	300
H&N	VMAT	70 (56)	132.9 (90.7)	2	132
	ROAD-75			25	1	77.28	150
	ROAD-150			25	1	105.13	300

3.2. Physical dose

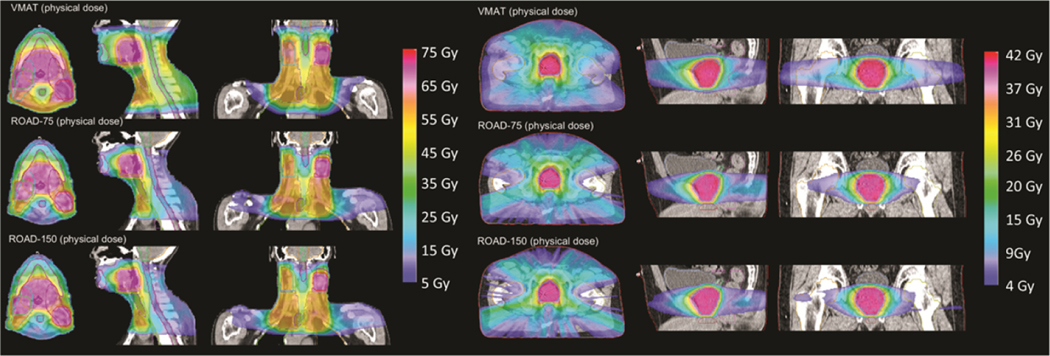
Figure 3 presents the isodose comparison of the physical dose of VMAT, ROAD-75, and ROAD-150 for the H&N and the PRT patient. ROAD-75 and ROAD-150 achieved similar OAR dose, while both significantly reduced OAR dose compared with VMAT. ROAD substantially reduced physical dose to the spinal cord and mandible for the H&N patient, and to the rectum, seminal vesicle, and penile bulb for the PRT patient.

Figure 3.

Isodose comparison of VMAT physical dose, and physical dose of ROAD-75 and ROAD-150 for the H&N and the PRT patient.

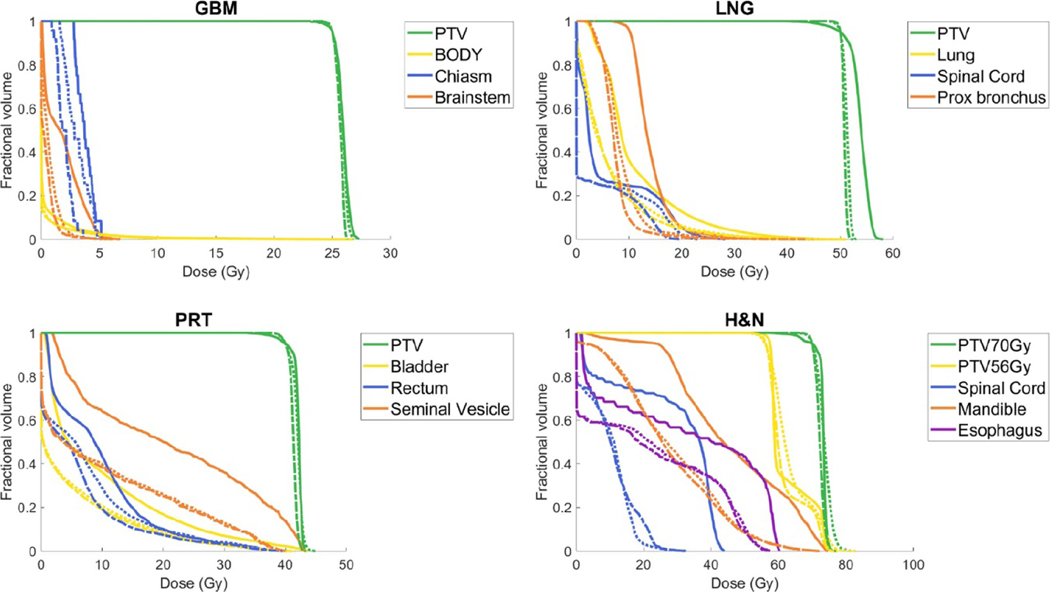
Figure 4 compares the physical dose DVHs of VMAT (solid), ROAD-75 (dotted), and ROAD-150 (dashed) for all patients. PTV D95 is normalized to prescription dose in all plans. ROAD-150 improved PTV homogeneity compared with the clinical VMAT plans and reduced physical dose to OARs.

Figure 4.

DVH comparison of VMAT physical dose (solid), ROAD-75 physical dose (dotted), and ROAD-150 physical dose (dashed) for all plans with selected OARs. PTV D95 is normalized to prescription dose in all plans.

Figure 5 reports the PTV and OAR statistics of the physical dose, comparing VMAT (green diamonds), ROAD-75 (orange circles), and ROAD-150 (blue crosses). Compared with clinic VMAT plans, ROAD-150 substantially improved PTV homogeneity, increased PTV minimum dose (D98), and reduced PTV maximum dose (D2). The PTV homogeneity improved by 3%, PTV D98 increased by 3%, and PTV D2 decreased by 3%. The R50, integral dose, and OAR mean and maximal dose were markedly reduced in the ROAD plans. Compared with clinical VMAT, ROAD-150 reduced the (max, mean) OAR physical dose by (4.8 Gy, 6.3 Gy). The average R50 and integral dose of (VMAT, ROAD-75, ROAD-150) are (4.8, 3.2, 3.2) and (89, 57, 56) Gy × l, respectively.

Figure 5.

Comparison of VMAT (green diamonds), ROAD-75 (orange circles), and ROAD-150 (blue crosses) on PTV statistics (Homogeneity, PTV D98 and D2 normalized by the prescription dose), R50, Integral Dose normalized by the prescription dose, and OAR maximum and mean doses.

3.3. FLASH dose

Figure 6 shows the heat map of physical dose and FD distribution of normal tissue voxels receiving physical dose greater than 10 Gy, based on the ROAD-150 plans for all patients, assuming 25 Gy prescription dose in a single fraction. The heat map was normalized columnwise. Overall, the ratio of FD to the physical dose is around 50% to 70%, indicating that the majority of the delivered physical dose could trigger the FLASH effect.

Figure 7 compares the physical Dose Volume Histogram (solid) and the FD Volume Histogram (dotted) of the ROAD-150 plan for the H&N patient. The FD takes up a large portion of the physical dose, especially in the high-dose region. For example, 30% of the trachea received no less than around 18 Gy of physical dose within a single fraction. In the meantime, 30% of the trachea received no less than around 13 Gy FD, indicating the biological damage to the trachea could be substantially lower with the ROAD delivery.

Figure 7.

Dose Volume Histogram (solid) and FLASH Dose Volume Histogram (dotted) of the ROAD-150 plan for the H&N patient.

3.4. FLASH biological equivalent dose

Figure 8 reports the statistical comparison of the physical dose (orange circles) and the FBED (purple squares) of ROAD-75 plans for all patients, assuming nominal parameter values and 25% uncertainty. The FBED under nominal parameter values substantially reduced R50, integral dose, and maximum and mean OAR doses compared with the physical dose, indicating potentially significant biological gains with ROAD plans. However, the large error bars also suggest large uncertainties due to the uncertainties in the biological model. Note that the FLASH effects are most evident in the high-dose regions, where the normal tissues receive a substantial dose that depletes transient oxygen and triggers the FLASH effect. For example, the H&N case has significantly higher OAR mean and maximal dose than other cases, and subsequently, it shows the most significant FLASH effect in OAR mean and maximal dose. However, all four cases showed substantial FLASH effects, as indicated by the sharp reduction of R50.

Figure 8.

Comparison of physical dose (orange circles) and the FLASH Biological Equivalent Dose (purple squares) with error bar of ROAD-75 plans for all patients on R50, Integral Dose normalized by the prescription dose, and OAR maximum and mean doses. The error bars show the min and max of the statistics assuming 25% uncertainty in the biological model parameters. The markers represent the normal case.

Figure 9 compares the physical Dose Volume Histogram (solid) and the FBED Volume Histogram (dotted) of the ROAD-150 plan for the H&N patient. The FBED were computed assuming nominal parameters and a single-fraction dose of 25 Gy. The OAR FBED was markedly reduced compared with the corresponding physical dose, indicating the FLASH effect could result in less OAR damage in the ROAD plans.

Figure 9.

Dose Volume Histogram (solid) and FLASH Biological Equivalent Dose Volume Histogram (dotted) of the ROAD-150 plan for the H&N patient, assuming nominal parameters in the FBED model and a single-fraction dose of 25 Gy.

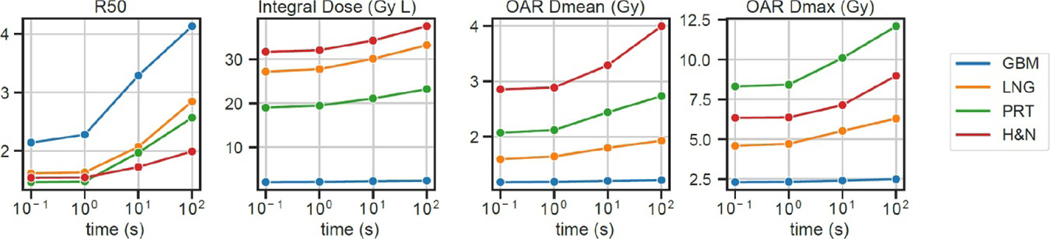
Figure 10 shows the time dependence of the ROAD-150-FBED. As delivery time increases from 0.1 s to 100 s, the R50, integral dose, and OAR Dmean and Dmax increase, reaching that of the physical dose with 100s delivery time. The dose compactness and OAR sparing substantially improved with shortened delivery time, and plateaued with a delivery time less than 1 s. Note that the results are dependent on the parameters in the FBED model. For example, if a greater diffusion constant were assumed, the oxygen would be replenished at a faster rate, leading to a shorter time threshold of observing the FLASH effect.

Figure 10.

Time dependence of the ROAD-150-FBED, evaluated for all patients over four metrics, including R50, integral dose normalized by the prescription dose, and OAR maximum and mean doses, assuming nominal parameters in the FBED model and a single-fraction dose of 25 Gy. The delivery time ranges from 0.1 s to 100 s. The OAR maximum and mean doses were the averaged values across all OARs for each individual patient.

4. Discussion

Existing treatment machines with a single MLC module are mechanically too slow for FLASH radiotherapy. This study proposes the novel ROAD design, which mounts 75 MLC modules on a separate ring and pre-shapes the apertures to achieve ultrafast dose modulation. We can find an analogy in computer science, where a space-time tradeoff manifests through solving a problem in less time by using more storage space or in limited space by spending extra time. ROAD and VMAT both enforce a single fluence map segment per beam, but they differ in delivery speed, the number of control points, and aperture continuity constraints: VMAT requires similar aperture shapes for adjacent beams, and ROAD-150 has the leaf speed constraint on the beams that share the same MLC modules. Without aperture continuity constraint on adjacent beams, ROAD plans can be delivered within 1 s, providing a viable solution for clinical FLASH radiotherapy.

Compared with clinical VMAT plans, ROAD-150 improved PTV homogeneity and substantially reduced OAR dose. The improvement in physical dose is attributed to the integrated optimization framework, which has been applied to VMAT optimization and was shown to outperform the progressive sampling optimization method used in clinical VMAT (Nguyen et al 2016). The potential FLASH effect further increases the therapeutic window in addition to the physical dose improvement. Apart from the improved physical dose, ROAD maintained the per-beam dose under 2 Gy for practical linac design and achieved a markedly higher mean dose rate. Previously reported studies indicated that the FLASH effect was observed when the mean dose rate is greater than 40 Gy s⁻¹. In this study, assuming a single-fraction dose of 25 Gy and treatment time of 1 s, the average per-beam dose rate is 76.2 Gy s⁻¹ and 112 Gy s⁻¹ for ROAD-75 and ROAD-150, respectively. 50% to 70% of the physical dose was delivered with equal to or greater than the FLASH threshold dose rate for ROAD to take advantage of the additional FLASH biological effects in addition to the improved physical dose. We note that the estimated percentage could vary with our continuously improving knowledge of the FD rate.

The ROAD system is a conceptual software and hardware platform for ultrafast radiotherapy delivery, where the optimization is based on the physical dose. Besides the main point, to demonstrate the feasibility of incorporating a quantitative FLASH biological model into planning, we selected the ROD model (Pratx and Kapp 2019) as an example to evaluate the biological effectiveness under various operational conditions. To employ ROD, we made several extensions to the original model. First, the original ROD paper (Pratx and Kapp 2019) only discusses the FLASH effects on a small subvolume, while we apply the model to the whole patient body. Solving the large-scale differential equation for a CT image containing tens of millions of voxels using parallel computing is not trivial. Second, the ROD paper focuses on the decreased radiosensitivity with varying parameters, whereas the current study calculates FBED based on the dose-averaged radiosensitivity. Third, we tailored the biological model to fit the ROAD model.

The FD and FBED models attempt to address one common challenge in FLASH radiotherapy, which is to evaluate the FLASH effect for radiation with complex spatial and temporal structures. In the ROAD plan delivery, the pulse dose rate is different from the instantaneous dose rate distributed within the patient body. For proton FLASH in the shoot-through mode, although a single proton field can be delivered with a high dose rate, the time to deliver multiple fields for conformal dose distribution will result in a low average dose rate, which would be significantly lower than the proposed FLASH system. The quantitative FD and FBED model is one way to reconcile the apparent conflict between the instantaneous dose rate seen by a subvolume and the average dose rate.

Nevertheless, we note that the radiolytic biological model in FBED computation only partially explains the FLASH effect (Hendry 2020), and its correctness is pending further experimental validation. For example, a limitation of the ROD model is that the model assumes the cells sufficiently far from capillaries (thus experiencing hypoxia) to experience significant FLASH effects. The limitation indicates an incomplete understanding of the FLASH mechanism. There are also large uncertainties in the parameters, such as the diffusion constant and the ROD rate, and a lack of threshold on the instantaneous dose rate to trigger the FLASH effect. These uncertainties could lead to large uncertainties in estimating the FBED, as shown in figure 8. Emerging evidence may result in revised or new quantitative FLASH biological models. We will update the evaluation of ROAD accordingly.

Different from PHASER (Maxim et al 2019), ROAD is designed based on scaling up existing technologies. For example, existing MLCs are used with a larger quantity. The high-speed slip ring gantry has been demonstrated by Reflexion (Hayward, CA) (Fan et al 2012). Nonetheless, there are challenges beyond the scope of the concept paper. The significantly larger high output linac will be more challenging to integrate with the high-speed gantry. It would not be trivial to design an x-ray target system that can withstand the high beam power. Moreover, to maximize the output, the linac will be flattening-filter-free (FFF). As a VMAT system, the dose rate inhomogeneity will be managed in ROAD as linear constant multipliers in the inverse optimization. Because FFF-VMAT has been extensively studied with the minimal dosimetric difference compared with flattened-field VMAT, the physical dose impact is expected to be minimal. On the other hand, since the linac output is defined by the peak output at the center of the field, the effective dose rate will be lower, particularly for larger targets. We would evaluate the change in FBED with a FLASH biological model or increase the linac output to compensate for the reduced dose rate. Finally, the RF power system is to be optimized for the burst-mode operation. We will develop individual engineering solutions for overcoming these challenges in future work.

5. Conclusion

The novel ROAD design achieves ultrafast dose delivery and improves physical dosimetry compared with clinical VMAT, providing a potentially viable engineering solution for x-ray FLASH radiotherapy.

Appendix

A1. Apply FISTA for optimizing the fluence map

FISTA requires the objective function to be the sum of a differentiable convex function with a Lipschitz continuous gradient and a simple convex function for which the proximal operator can be evaluated efficiently. To facilitate FISTA, the nondifferentiable l₁ norm is smoothed using Moreau-Yosida regularization (Parikh and Boyd 2013) with parameter μ. The resultant smoothed function is the Huber penalty function (Huber 1964), defined as

$$H(x)=\parallel x{\parallel }_1^{(\mu )}=\sum _i{\left|x_i\right|}^{(\mu )},$$

Where

$${\left|x_i\right|}^{(\mu )}=\{\begin{array}{l}\frac{1}{2\mu }{x}_i^2,\left|x_i\right|\le \mu \hfill \\ \left|x_i\right|-\frac{\mu }{2},\left|x_i\right|>\mu .\hfill \end{array}$$

The Huber penalty function is a convex, differentiable approximation to the l₁ norm, with a $\frac{1}{\mu }$ Lipschitz continuous gradient.

To show that the equation (2) can be reformulated into the FISTA canonical form shown in equation (3), we first define two functions

$$F(f)=\frac{1}{2}W{\left(Af-d_0\right)}_2^2+{\lambda }_x{D}_x{f}_1^{(\mu )}+{\lambda }_y{D}_x{f}_1^{(\mu )}+\frac{\gamma }{2}\left[diag{\left(u_{\theta }\right)}^{1/2}{(f-c)}_2^2+diag{\left(1-u_{\theta }\right)}^{1/2}{f}_2^2\right]$$

$G(f)=I_{+}(f),$ (6)

where

$$I_{+}(f)=\{\begin{array}{l}0\text{if}f\ge 0\hfill \\ \infty \text{otherwise,}\hfill \end{array}$$

$$A=\left[\begin{array}{c}{A}_{\theta =1}{A}_{\theta =2}\cdots A_{\theta =n_{\theta }}\end{array}\right],$$

$$D_x=diag\left(D_{x,\theta =1},\dots ,D_{x,\theta =n_{\theta }}\right),D_y=diag\left(D_{y,\theta =1},\dots ,D_{y,\theta =n_{\theta }}\right)$$

$$f={\left[\begin{array}{c}{f}_{\theta =1}^T{f}_{\theta =2}^T\cdots f_{\theta =n_{\theta }}^T\end{array}\right]}^T,$$

$$u={\left[\begin{array}{c}{u}_{\theta =1}^T{u}_{\theta =2}^T\cdots u_{\theta =n_{\theta }}^T\end{array}\right]}^T,$$

$$c={\left[\begin{array}{c}{c}_{\theta =1}{\overrightarrow{1}}^T{c}_{\theta =2}{\overrightarrow{1}}^T\cdots c_{\theta =n_{\theta }}{\overrightarrow{1}}^T\end{array}\right]}^T,$$

With F and G defined as above, F (x) + G (x) is equivalent to the original optimization problem with smooth approximation and can be solved through FISTA as shown in Algorithm 1. In each iteration, the key steps are the evaluation of the gradient of F and the proximal operator of G.

The gradient of F can be evaluated by

$$\nabla F(f)=A^T{W}^2(Af-d)+\frac{{\lambda }_x}{\mu }{D}_x^T{P}_{[-\mu ,\mu ]}\left(D_{x}f\right)+\frac{{\lambda }_y}{\mu }{D}_y^T{P}_{[-\mu ,\mu ]}\left(D_{y}f\right)+\gamma diag(u)(f-c)+\gamma diag(1-u)f.$$

The proximal operator is defined as (Parikh and Boyd 2013)

$$Pro{x}_{tG}(x)=\underset{z}{argmin}\left\{G(z)+\frac{1}{2t}\parallel z-x{\parallel }_2^2\right\},$$

for a function G with step size parameter t. The proximal operator of G can be computed by

$$Pro{x}_{tG}(f)=\max (f,0).$$

Algorithm 1:

FISTA with line search

$\text{Initialize}{x}_0:=0,v_0:=x_0,t_0>0,r_1>1,r_2>1$

$\text{For}k=1,2,\dots \text{do}$

$t:=r_1{t}_{k-1}$

Repeat

$\theta :=\{\begin{array}{c}1\text{if}\text{k}=1\\ \text{positive}\text{root}\text{of}{t}_{k-1}{\theta }^2=t{\theta }_{k-1}^2(1-\theta )\text{if}\text{k}>1\end{array}$

$y:=(1-\theta )x_{k-1}+\theta v_{k-1}$

$x:=Pro{x}_{tG}(y-t\nabla F(y))$

$\text{Break}\text{if}F(x)\le F(y)+\nabla F(y),x-y+\frac{1}{2t}\parallel x-y{\parallel }_2^2$

$t:=t/r_2$

$t_k:=t$

${\theta }_k:=\theta$

$v_k:=x_k+\frac{1}{{\theta }_k}\left(x-x_k\right)$

$\text{Break}\text{if}\frac{x-x_k}{x_k}\le ϵ$

$x_k:=x$

End for

Return x

A2. Finite difference method

Here we derive a finite-difference method to numerically approximate the PDE in equation (5). Let Δt and Δr be small positive numbers representing the small increments in time and distance from the capillary, and let i and j be the temporal and spatial index of the matrix representation of the oxygen tension p:

$$\frac{\partial p}{\partial t}\approx \frac{p(t+\text{Δ}t,r)-p(t,r)}{\text{Δ}t}=\frac{p_{i+1,j}-p_{i,j}}{\text{Δ}t},$$

$$\frac{\partial p}{\partial r}\approx \frac{p(t,r+\text{Δ}r)-p(t,r)}{\text{Δ}t}=\frac{p_{i,j+1}-p_{i,j}}{\text{Δ}r},$$

$$\frac{{\partial }^{2}p}{\partial r^2}\approx \frac{p(t,r+\text{Δ}r)-2p(t,r)+p(t,r-\text{Δ}r)}{\text{Δ}{r}^2}=\frac{p_{i,j+1}-2p_{i,j}+p_{i,j-1}}{\text{Δ}{r}^2},$$

where$p_{i,j}=p\left(t_0+i\text{Δ}t,r_0+j\text{Δ}r\right)$.

Equation (5) is then represented in the discrete form:

$$\frac{p_{i+1,j}-p_{i,j}}{\text{Δ}t}=a\frac{p_{i,j+1}-2p_{i,j}+p_{i,j-1}}{\text{Δ}{r}^2}++\frac{a}{r_j}\frac{p_{i,j}-p_{i,j-1}}{\text{Δ}r}-m$$

where $r_j=r_0+j\text{Δ}r.$

Let$k=a\text{Δ}t/\text{Δ}{r}^2$, then

$$p_{i+1,j}=p_{i,j}+k\left(p_{i,j+1}-2p_{t,j}+p_{i,j-1}+\frac{\text{Δ}r}{r_j}\left(p_{i,j}-p_{i,j-1}\right)\right)-m\text{Δ}t,$$

and equivalently

$$p_{i+1,j}=k\left(1-\frac{\text{Δ}r}{r_j}\right)p_{i,j-1}+\left(1+\left(-2+\frac{\text{Δ}r}{r_j}\right)k\right)p_{i,j}+k{p}_{i,j+1}-m\text{Δ}t.$$ (7)

Equation (7) can be represented as an affine equation in homogeneous coordinates by defining:

$$p_i^{’}=\left[\begin{array}{c}{p}_{i,j=1}\\ ⋮\\ p_{i,j=N_j}\\ 1\end{array}\right].$$

Then equation (7) is equivalent to

$$p_{i+1}^{\prime }=M{p}_i^{\prime }$$

where

$$\{\begin{array}{l}M(j,j-1)=k\left(1-\frac{\text{Δ}r}{r_j}\right)\hfill \\ M(j,j)=1+\left(-2+\frac{\text{Δ}r}{r_j}\right)k\hfill \\ M(j,j+1)=k\hfill \\ M\left(j,N_j+1\right)=-m\text{Δ}t.\hfill \end{array}$$

The original PDE in equation (5) can be solved by iteratively applying the matrix M on the current state of the oxygen tension vector $p_i^{\prime }$in homogeneous coordinates. Without the nonnegative constraint, the solution to the PDE is

$$p_i^{\prime }={(M)}^{N_t}\cdot p_0^{\prime }$$

where$N_t=\left(t-t_0\right)/\text{Δ}t$. To enforce the nonnegative constraint and for computational efficiency, we project the oxygen tension vector p to the nonnegative orthant at each 1000 iterations:

$$\{\begin{array}{l}{p}_{i+1000}^{\prime }={(M)}^{1000}\cdot p_i^{\prime }\hfill \\ p_{i+1000}=P_{+}\left(p_{i+1000}^{\prime }\right)\hfill \end{array}$$