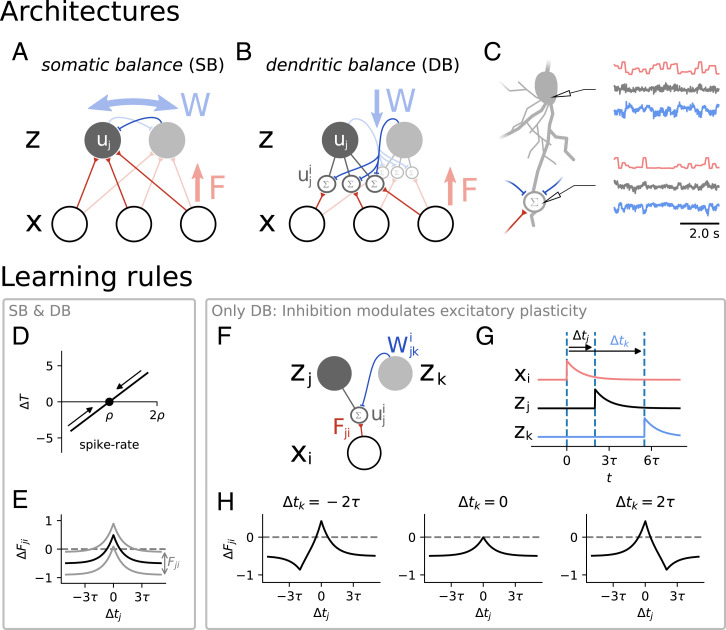
Fig. 2.

We compare learning in two network models, a point neuron model with somatic balance, and a model with dendritic balance. (A) In the model with SB, neurons (gray circles) with outputs z receive feedforward network inputs x (white circles) and are coupled via recurrent connections. Recurrent weights W are adapted to balance other inputs to the somatic membrane potential u_j, which ensures an efficient spike encoding. (B) In our proposed model with DB, neurons receive inputs at specific dendritic compartments. Recurrent connections learn to balance input currents locally at the dendrites. This leads to dendritic potentials $u_j^i$ that are proportional to the coding error for specific feedforward inputs and therefore can be used to learn feedforward weights. (C) After learning, local feedforward (red) and recurrent (blue) currents have adapted to tightly balance each other in individual dendritic compartments (Bottom). This dendritic balance also results in a somatic balance of inputs (Top). Here we show a neuron from a network with 80 neurons coding for natural images. (D) In both models a rapid compensatory mechanism ensures that every neuron fires with rate ρ. If any neuron spikes too rarely, its threshold T_j is lowered; if it spikes too often, T_j is increased. (E–H) Illustration of learning rules in terms of experimental STDP rules. For easier interpretability we plot weight changes for spiking inputs x_i, whereas in the remainder of this paper, x_i are analog input signals. (E) For learning feedforward weights in the point neuron model (SB) a Hebbian-like STDP rule increases or decreases weights F_ji depending on the time difference between pre- and postsynaptic spikes $\mathrm{\Delta }{t}_j$ and the weight F_ji itself. If F_ji is high or low, this shifts plasticity toward depression or potentiation, respectively. The same learning rule applies to the DB model, if a neuron does not simultaneously receive any recurrent input. (F–H) Illustration of how inhibition modulates feedforward plasticity in the proposed model for a network of two coding neurons z_j (with one dendritic compartment) and z_k and one input neuron x_i. (F) The excitatory weight F_ij and the inhibitory weight $W_{jk}^i$ attach to the same dendritic potential $u_j^i$. (G) We consider the following example where three spikes are fired: x_i at t = 0, z_j at $t=\mathrm{\Delta }{t}_j$, and z_k at $t=\mathrm{\Delta }{t}_k$. (H) The total change in the weight F_ji depends not only on the spike time difference $\mathrm{\Delta }{t}_j$ between the input and the postsynaptic neuron, but also on the relative inhibitory spike time $\mathrm{\Delta }{t}_k$. In general, if z_j and z_k spike close together, F_ji will tend to be depressed. All weight changes were calculated with $F_{ji}=-W_{jk}^i=0.5$.