Lifetime-based analysis of binary fluorophores mixtures in the low photon count limit

Summary

Single biomolecule sensing often requires the quantification of multiple fluorescent species. Here, we theoretically and experimentally use time-resolved fluorescence via Time Correlated Single Photon Counting (TCSPC) to accurately quantify fluorescent species with similar chromatic signatures. A modified maximum likelihood estimator is introduced to include two fluorophore species, with compensation of the instrument response function. We apply this algorithm to simulated data of a simplified two-fluorescent species model, as well as to experimental data of fluorophores' mixtures and to a model protein, doubly labeled with different fluorophores' ratio. We show that 100 to 200 photons per fluorophore, in a 10-ms timescale, are sufficient to provide an accurate estimation of the dyes' ratio on the model protein. Our results provide estimation for the desired photon integration time toward implementation of TCSPC in systems with fast occurring events, such as translocation of biomolecules through nanopores or single-molecule burst analyses experiments.

Graphical abstract

Highlights

• •Exact ratios of emission-similar dyes in binary mixtures were quantified by TCSPC
• •MLE-based analysis with IRF compensation was implemented for two fluorescent dyes
• •Dual dye bioconjugation on a model protein was quantified at limited photon counts

Computational chemistry; Optics; Biophysics; Laser biophysics

Introduction

The ability to discriminate among multiple fluorescent species in labeled biomolecules is a fundamental requirement for a variety of sensing applications ranging from DNA sequencing techniques to protein quantifications, in vitro and in vivo (Alfaro et al., 2021; Joo and Ha, 2012; Kapanidis et al., 2015; Swaminathan et al., 2018; Van-Ginkel et al., 2018). In most cases discrimination among fluorescent species is achieved using fluorophores with distinctively different excitation and/or emission spectra, hence permitting chromatic separation of the emitted photons into multiple detection channels. Specifically, single molecule techniques, such as photon bursts analysis and fluorescence resonance energy transfer (smFRET) often involve spectral discrimination. But the ability to quantitively resolve multiple fluorescent species based solely on their emitted photon wavelength bands involves difficulties that complicate measurements, particularly when the total photon quota for the analysis is scarce. For example, channel to channel bleed-through and non-uniform detection efficiencies among multiple channels complicate single-molecule FRET efficiency determination for both immobilized and in photon-burst analyses (Sabanayagam et al., 2005). Another example for the use of multi-species single-molecule fluorescent sensing involves electro-optical sensing in nanopores (Gilboa and Meller, 2015). Multi-color detection has been applied to quantify epigenetic modifications and distinguish among labeled polypeptides (Gilboa et al., 2016; Wang et al., 2018) as well as DNA fragments representing different cancer-related mutations as they translocate through a synthetic nanopore (Burck et al., 2021). Of note, the voltage-driven translocation of the fluorophores results in short molecular dwell times that can substantially limit the number of photons available for multi-color analysis hence posing a challenge to precisely distinguishing among species (Ohayon et al., 2019).

Non-chromatic discrimination of multiple fluorescent species has been achieved using fluorescence lifetime (FLT) measurements. For example, Kremers and coworkers described a quantitative unmixing method based on single frequency domain fluorescence lifetime imaging microscopy (Kremers et al., 2008). More recently, the combination of spectral and lifetime signals was demonstrated in FLIM (“spectral-FLIM”) for blind unmixing of spectral and lifetime signatures from multiple unknown species (Scipioni et al., 2021). Moreover, FLT has been broadly applied in combination with spectral separation to enhance single molecule discrimination using multi-parameter fluorescence detection (MFD) strategies (Kalinin et al., 2010).

Unlike frequency-domain FLIM, time-correlated single-photon counting (TCSPC) accumulates data from single-photon events emitted by single fluorophores. In TCSPC, the mean lifetime information is obtained from modeling the histogrammed raw data of multiple single-photon lifetimes measurements, emitted by either a single molecule or multiple molecules. Maximum likelihood estimation (MLE) procedures have been found to be extremely efficient for the analysis of TCSPC data of a single-component sample (Hall and Selinger, 1981) as well as for the analysis of surface immobilized single-molecule FRET data (Edel et al., 2007). Studies to date involving smFRET and FLIM either exploited the measurements of FLT in multiple color channels in order to enhance the robustness or accuracy of the measurement or used this information to gain knowledge on the photophysical behavior of the dyes (Kaye et al., 2017) (Höfig et al., 2014)(Sheng et al., 2008). Other studies used laser scanning-based FLT measurements or large-area FLIM for live cell FLIM (Oleksiievets et al., 2020; Raspe et al., 2016) (Blacker et al., 2014; Grecco et al., 2010; Lagarto et al., 2020; Ma et al., 2021; Scipioni et al., 2021).

FLIM, optical nanopore sensing, as well as other applications of FLT may nevertheless benefit from the ability to resolve multiple fluorescence species in each of the excitation/emission channels, as a way to further increase the methods' multiplexibility, while preserving single-molecule resolution. To this end we computationally and experimentally explore the case of a single emission band (i.e., a single detector), two species unmixing in the limit of low photon emission, which is most relevant for single-molecule sensing. We begin by presenting numerical simulations that consider Poisson photon noise, as well as the Instrument Response Function (IRF) of the experimental system to evaluate the expected ability to quantitatively measure the relative concentration of two dye species that practically exhibit an identical emission spectra. We evaluate our results in the context of two scenarios: (1) the ability to accurately predict the species concentration ratio in a binary mixture, and (2) the ability to probabilistically discriminate among the two fluorophore species given a limited number of time-resolved photons. We then experimentally validate our predictions in two types of experiments: (1) dilute binary mixtures of the two dyes analyzed by photon bursts using single channel TCSPC, and (2) dually labeled proteins in which both fluorophores' photons are captured during the diffusion of the proteins through the confocal excitation volume. Both in our simulations and experimental analysis we consider the IRF's contribution to the TCSPC data. In accordance with previous studies (Edel et al., 2007) (Maus et al., 2001) (Nishimura and Tamura, 2005), we find that, in either case, MLE-based analysis yields optimal results when photon budget is highly limited. When applying our analysis to dually labeled proteins (with two fluorophores species having nearly identical emission spectra), we found that, owing to the discreteness of the possible ratio states, the required photon budget for high confidence determination is significantly reduced to a few tens of photons per fluorophore.

Results

Monte Carlo simulations for lifetime measurements of unitary or binary fluorophore systems

To guide us on the optimal fluorescent species lifetimes and to set our expectation on the photon budget required for discrimination, we performed an extensive set of Monte Carlo (MC) simulations. Each generated photon in the simulation is randomly obtained based on the pure lifetime distribution probability function (including a single or biexponential function for unitary or binary fluorophore systems, respectively) and the data is “contaminated” with two sources of noise: (1) Poisson photon noise, and (2) the normalized IRF, obtained experimentally. For each “quota” of the generated photons in the MC simulations we first evaluated the most likely fluorescence lifetime using MLE model and present the result as the fractional ratio of the absolute deviation of the obtained value (τ_fit) from the set value (τ_set), namely, $\left|{\tau }_{fit}-{\tau }_{set}\right|/{\tau }_{set}$ in percentile (Figure 1A). Our results clearly suggest that, for a single component system <300 photons are sufficient to recover the mean lifetime with a deviation that is <30%. Particularly, for the shorter lifetimes <20% is obtained with as low as 200 photons.

Figure 1.

Monte Carlo simulations for single or dual fluorophore species

(A) The expected deviation (in %) for the determination of the fluorescence lifetime, defined as $\left|{\tau }_{fit}-{\tau }_{set}\right|/{\tau }_{set}$ of a single fluorescent species as a function of total number of detected photons.

(B) The expected deviation (in %) in MLE-based determination of the two fluorophore (Atto 565 and Atto Rho3) species' molar ratio (r_fit), as a function of their actual mixing ratio (r), defined as $\left|r_{fit}-r\right|/r$. In both cases the IRF (see Figure S3) and Poisson noise were added to the generated data prior to the MLE fitting. The insets represent the averaged deviations for all lifetimes and ratios, respectively.

Next, we evaluated the deviation for the MLE-derived dyes' ratio in binary mixtures, as a function of their actual molar ratio r, namely, $\left|r_{fit}-r\right|/r$. Our simulations results shown in Figure 1B indicate that, in order to correctly predict the ratio of the two components in a binary mixture, a larger quota of photons is required. At least 5,000 photons were required to obtain the dyes' ratio with deviation <30%. An equal molar binary mixture (r = 0.5) yields the best result requiring as low as 1,000 photons with <30% deviation, or conversely predict the ratio with <5% deviation if the photon quota was kept at 5,000. Overall, the system can predict the dyes' ratio at all values simulated (from 1:10 to 10:1 stoichiometric ratios) with <10% deviation provided that the total photon quota was 10,000 or more.

TCSPC experiments of freely diffusing dye samples

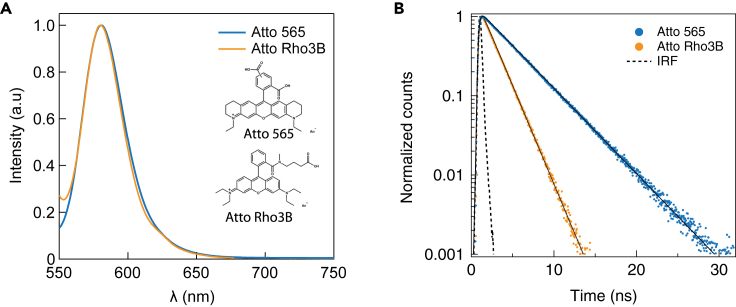
Two fluorescent dyes, ATTO 565 and ATTO Rho3B (ATTO-Tec, GmbH), having nearly identical fluorescence emission spectra and readily distinguishable fluorescence lifetimes were used in this study, as shown in Figure 2A. The lifetime measurements, performed on the individual dyes' solutions, each showed single exponential lifetimes (Figure 2B) with relatively insignificant deviations (4.02 ± 0.20 ns for the Atto 565 and 1.75 ± 0.08 ns for the Atto Rho3B), obtained by MLE-fits (solid lines) that take into account the measured IRF (dashed line).

Figure 2.

Emission spectra and lifetime characterization of the fluorophores used in this study

We used two fluorophores in this study (Atto 565 and Atto Rho3B, blue and orange, respectively) in bulk.

(A) The normalized fluorophores' emission spectra of the two dyes.

(B) TCSPC fluorescence lifetime measured in aqueous buffer of the dyes and IRF (instrument response function) of our system (see also Figure S3). Solid black curves are fits, taking into account the IRF, giving apparent lifetimes of 4.02 ± 0.20 and 1.75 ± 0.08 ns for the Atto 565 and Atto Rho3B, respectively.

Next, we examined binary mixtures of the two dyes in our experimental apparatus. Briefly, the setup consists of a home-build confocal microscope, as shown schematically in Figure 3A (see also the STAR Methods section). The start and stop pulses were taken from the pulsed laser driver and from a Single Photon Avalanche Photodiode (PDM 100ct, MPD). TCSPC data were acquired using either a TimeHarp 200 (PicoQuant, GmbH) or Multiharp 150 electronics (PicoQuant, GmbH). The TCSPC signals were acquired at 10 MHz repetition rate producing a count rate of a range 5,000–10,000 cps, unless specified differently. To evaluate the fluorescence lifetime estimation, we randomly selected N photons from the datasets and used the MLE model to fit the data, as described in the STAR Methods section.

Figure 3.

Experimental TCSPC results of samples with a single fluorophore species

(A) TCSPC experimental layout.

(B) The deviation in the experimental determination of the individual fluorophore component (calculated as in Figure 1) as a function of the photon quota used in the analysis. The insets display examples of the TCSPC data for N = 1,000 photons (all other cases provided in Figure S4) and the MLE fits.

Figure 3B insets show examples (N = 1,000 photons) of the experimentally obtained TCSPC data fitted using the MLE (solid lines) of the two fluorophores analyzed separately. We analyzed the deviation of the MLE fit results from the respective fluorophores lifetime shown in Figure 2 as a function of the number of photons used in the analysis. Consistent with the MC simulations shown in Figure 1A, we see that the shorter lifetime fluorophore (Atto Rho3B) was determined with smaller deviation than the Atto 565 when the photon quota is limited, but above roughly 1,000 photons their respective deviations are nearly identical. The fact that the experimental data of the separate components qualitatively match the MC simulation of the same system validates the assumptions made in the MC simulation, namely, the inclusion of Poisson noise and the system IRF, as well as the MLE procedure for fitting the data. This verification is essential before testing the fluorophore mixtures experimentally, which add few additional experimental unknowns to the system.

To evaluate the ability of our method to precisely determine the relative concentration ratios in binary mixtures of the two fluorophores, we prepared a set of 17 different concentration ratios (determined volumetrically) in the range of 0.1–0.9 characterized by:

$$\begin{array}{l}r=\frac{C_{ATTO565}}{C_{ATTO565}+C_{ATTORho3B}}\hfill \end{array}$$ (Equation 1)

The concentration of the individual components was determined using UV-vis absorbance at their corresponding absorbance maxima. These concentration ratios correspond to a range of roughly 0.11–9 in stoichiometric ratio x, by the conversion x = r/(1−r). Each of the binary mixtures was subject to a similar TCSPC analysis, as performed for the single component solution. However, in contrast to the single-component case after randomly selecting a fixed number of photons from the acquired data stream, we used a double exponential MLE model approximation (see STAR Methods section), which returns the relative weight of the two lifetimes components in the system. In an analogous way to the analysis of the MC simulations results for the binary mixture (Figure 1B), for each molar mixing ratio (r) we calculated the deviation in the determination of the stoichiometric ratio in the mixture comparing the experimentally estimated ratio at limited photon number (N) with the value obtained for N > 10⁶ photons. Our data is summarized in the heatmap Figure 4A. We first note that the experimental results closely reproduce the trends observed in the MC simulations, namely, the optimal determination of the fluorophores ratio is obtained around r = 0.5 where <5,000 photons are sufficient to quantitively predict r with <10% deviation. Moreover, even near the extreme r values (0.2 and 0.8) about 10,000 photons are sufficient for r determination with better than 20% accuracy. The error in the determination of r values is shown for three values as a function of the number of photons in the inset of Figure 4A.

Figure 4.

Experimental TCSPC results of samples with binary mixtures of the two fluorophore species

(A) The relative deviation in the determination of the molar ratio r, as a function of the total number of photons used in the analyses. The deviation is calculated from the normalized difference between the experimentally determined dyes' ratio at finite number of photons (r_N) to the value obtained using the full data set (>10⁶ photons) defined as r_exp. Inset: Typical line plots of the fluorophore error determination for three specific ratios.

(B) Comparison of the absolute values of the experimentally determined ratio (r_exp) versus the preparation molar ratio (r) shows a systematic bias, associated with the different fluorophores' brightness ratio as explained in the text.

To check for systematic deviations in our method, we next compared the TCSPC-determined dyes ratio with extremely high photon count (r_exp) with the dyes ratio determined during the preparation of the samples (r), as defined in Equation 1. Our results, shown in Figure 4B, indicate that the experimental data do not show a linear dependency on the prepared ratio. This, however, is expected as the two fluorophores have different brightness values: Atto 565 QE = 0.9 and absorbance maximum of 1.2⋅10⁵ M⁻¹cm⁻¹ at 590 nm, whereas the Atto Rho3B QE = 0.5 and its absorbance maximum is 1.2⋅10⁵ M⁻¹cm⁻¹ at 589 nm, as provided by the manufacturer (Atto-Tec, GmbH). We therefore expect that the effective number of photons emitted by the Atto 565 fluorophore is nearly double compared with that of the Atto Rho3B fluorophore. To account for this simple correction, we fit our data (Figure 4B) with the following function that connects the experimentally determined dyes ratio with the molar preparation ratio and includes just a single adjustable parameter:

$$\begin{array}{l}{r}_{exp}=\frac{1}{1+\frac{1}{\beta \cdot x}},\hfill \end{array}$$ (Equation 2)

where r_exp is the ratio of the dyes as measured by TCSPC. Fitting the data to Equation 2 yields β = 2.15 ± 0.03. This value is within experimental error for the brightness ratios B_{ATTO 565}/B_ATTO Rho3B as determined by integration over their corresponding emission spectra of the fluorophores' solution prepared at the same concentration and measured using the exact same fluorospectrometer settings (see Figure S1).

Dual-labeled protein analyses using a single-color TCSPC

After examining our ability to quantify freely diffusing binary mixtures of fluorophores, we next analyzed samples of dually labeled proteins. Here lysine residues of the protein ovalbumin (OVA) were conjugated using different ratios of the NHS-ester derivatives of the two fluorophores (Atto 565 and Atto Rho3B). OVA harbors 20 lysine (K) amino acid residues (see Figure S2 for the amino acid sequence), but only a fraction of them is available for NHS-ester conjugation in the protein's native folded state. To estimate the degree of proteins labeling we used bulk UV-vis absorbance and quantitative fluorospectrometry. Of note, owing to the relatively high specific absorbance of the fluorophores (at 565 nm) as compared with that of the proteins (280 nm) and the fact that the fluorophores may bias the absorbance around 280 nm, an accurate measurement of the dye/protein molar ratio for high fluorophore labeling is unreliable. Instead, we prepared a set of known dye/protein labeling ratios and systematically measured their fluorescence intensity after removal of the unconjugated dyes. As the dye to protein ratio increases, we see a linear increase in the fluorescence intensity, reaching an apparent plateau when this ratio exceeds 10 (Figure 5A). This suggests that under these native conditions, 10 lysine residues per OVA molecule are accessible for NHS-ester dyes conjugation.

Figure 5.

Analysis of dually labeled Ovalbumin (OVA) proteins using NHS ester reactive dyes

(A) Bulk fluorescence intensity of different labeling levels of the OVA after removal of the unconjugated dyes, showing an apparent plateau at a ratio of >10 Atto 565 NHS ester per protein molecule.

(B) The relative deviation (%), calculated as in Figure 4, in the determination of the dyes' ratios calculated using different number of photons for the 9 OVA samples. The experimentally determined r_N is performed by TCSPC as described in the text. Inset shows the accumulated averaged error for all the different ratios measured in our experiments.

We prepared a set of nine OVA samples labeled using mixtures of the two NHS-ester dyes in the range r = 0.1–0.9 as defined by Equation 1. All the samples were analyzed using the TCSPC setup and the MLE-fit procedure, as described in Figure 3 and in the STAR Methods section, to obtain the experimentally determined ratio of the two dyes r_N as a function of the number of photons. Similarly to the analysis of the binary free-solution mixtures, the photons emitted by the two dyes are randomly mixed and our analysis model can only treat their statistical properties. Figure 5B shows the deviation of the experimentally determined dyes ratios using N photons from the corresponding value obtained with very large number of photons (r_exp). When N > 25,000, all dyes ratios can be determined with relatively small deviations (typically <20%), but for a lower number of photons, a clear bias, in favor of the Atto Rho3B dye, emerges. For small r values (i.e., 0.2 or less) we obtain smaller deviations for the ratio determination as compared with the larger r values (r > 0.7). We evaluated the statistical scatter of our ratio determination by repeating the MLE fits 100 times, each time randomly choosing N photons from the data stream. This analysis shows that, as long as N > 1,000 photons, the mean r_N values fall within their corresponding STDs. But below 1,000 photons we observe a significant decrease in the mean r_N (see Figure S5). Nevertheless, our experimental and simulation data suggest that it is possible to accurately determine the fraction of two fluorophore species conjugated to the same protein molecule with relatively small number of photons. In some cases, about 10,000 photons are sufficient to determine the actual dye absolute ratio. Since 10 fluorophores are conjugated per OVA protein, this amounts to 1,000 detected photons per dye, on average.

The relatively large deviation obtained when using typically <5,000 photons in the analysis of the TCSPC data as shown in Figure 5 may raise the question if an accurate species determination is at all feasible in single-molecule measurements performed at an extremely low photon budget. However, from a statistical standpoint, if we include knowledge on the analytes in our mathematical analysis, we can reduce the number of required photons, while preserving a robust determination of species ratios. Particularly, in the case of labeled proteins there is a finite number of lysine residues (or primary amines) available for NHS-ester reactions. Assuming that all available free lysine sites are labeled (this is a reasonable assumption as we carry the labeling reaction to completion) for the OVA proteins r can take one of nine values, corresponding to dyes' stoichiometric ratios, i.e., 9:1, 8:2, …, 1:9. This argument holds true also for other types of bioconjugations in which the chemical nature of the labeled molecule imposes a known constriction on the possible r values in each single molecule. With this assumption, we can reevaluate the deviation of determining one of the nine possible r values based on the TCSPC data using $\frac{\left|r_{exp}-r_N\right|}{{\sum }_{i=1}^9{r}_{ex{p}_i}}$, as shown in Figure 6.

Figure 6.

Accurate quantification of fluorophores' ratio at low photon budget is achieved for discrete r values

(A) The deviation in determining the dually labeled proteins' dyes ratio based on TCSPC analysis, as a function of the total number of photons (N) used in the analysis. Since there are nine possible labeling ratios of the protein, the error for each sample is evaluated as: $\frac{\left|r_{exp}-r_N\right|}{{\sum }_{i=1}^9{r}_{ex{p}_i}}$.

(B) The averaged deviation values in determining all the different r values for all samples, as a function of number of photons.

Interesting, we observe that, for most of the possible r values, roughly 2,000 photons are sufficient to experimentally obtain the dyes' ratios with a deviation <5% and roughly 1,000 photons for <10% deviation. Since the OVA proteins are labeled by a total number of 10 fluorophores, these numbers correspond to an average of 200 or 100 photons/dye molecule for the 5% and 10% deviations, respectively.

Discussion

The ability to discriminate among multiple fluorescent species conjugated to the same biomolecule or organelle and quantify their ratio is a general challenge in life sciences and in single-molecule applications, most commonly addressed by using multiple fluorescent dyes with distinct excitation/emission spectra. Here we computationally and experimentally evaluated the possibility of substituting or complementing the chromatic separation of the signal with time-resolved information, based exclusively on TCSPC. We implemented an MLE-based analysis, which involves the two fluorophores' photon emission probability functions, the experimental IRF, and the noise of the system. For binary dyes mixtures, we find that absolute ratios can be determined with relatively low deviation, if the total photon budget available for the analysis exceeds >10,000 for a broad range of the dyes' ratio. But using a smaller photon budget the absolute dyes ratio determination deviation increases significantly, limiting its potential use for “single-shot” (a single passage through the detection volume) ratio analysis.

We extended our measurements for dual bioconjugation of OVA protein molecules, used as a model. In this case, as well as in many other bio-labeling cases, the possible two species labeling ratios are constrained by the total number of amino acids available for labeling (lysines in this case) and the discrete nature of the chemical labeling reaction. Specifically in the OVA case, nine possible labeling ratios were considered. Taking this into consideration in our analysis, we find that it significantly reduces the required photons budget in order to achieve the two dyes' ratio with small deviation. For example, to obtain the ratio with 10% deviation, about 100 acquired photons per dye are needed. If we assume a realistic single fluorophore emission rate of about 10 detected photons per millisecond based on single-molecule experiments (Di-Fiori and Meller, 2010), our results would imply a practical dwell time of about 10 ms for each single protein molecule in the emission zone. These results may be helpful in designing emerging technologies for protein quantification, protein sequencing, and other biomolecules sensing.

Limitations of the study

For our results to be valid, we assume that the efficiencies of dye conjugation to the protein are relatively high. Specifically, although we do not assume that all lysine residues and primary amines in the model protein OVA are available for labeling, we do assume that the available residues are fully (or nearly fully) conjugated. This assumption may not be completely general to all proteins and must be verified experimentally under different conditions in future studies. To minimize fluorophore quenching phenomena, the TCSPC measurements were performed under denatured conditions, which are most relevant for emerging protein sequencing applications (Alfaro et al., 2021). We note, however, that some other applications may involve folded proteins, which may further complicate the MLE data analysis. Fluorescence lifetime is known to be an extremely efficient tool for evaluating inter- and intra-energy transfer among fluorophores, hence opening new avenues for further studies. Moreover, to further confirm our study's conclusions and the correlation between the experimental TCSPC results with the MC simulations, additional pair of fluorophores, having a different set of intrinsic lifetime values should be considered. For performing a more accurate statistical analysis of the photons acquired from labeled proteins, the simulations should include the inaccuracies that result from interactions of fluorophores residing in close proximity, such as energy transfer.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Chemicals, peptides, and recombinant proteins
Albumin from chicken egg white (aka. Ovalbumin)	Sigma-Aldrich	A2512; CAS: 9006-59-1
Carboxy Atto 565	ATTO-Tec GmbH	AD 565-25
NHS-ester Atto 565	ATTO-Tec GmbH	AD 565-35
Carboxy Atto Rho3B	ATTO-Tec GmbH	AD Rho3B-25
NHS-ester Atto Rho3B	ATTO-Tec GmbH	AD Rho3B-35
Software and algorithms
MatLab	MathWorks	https://www.mathworks.com/login

Resource availability

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Prof. Amit Meller (ameller@technion.ac.il).

Materials availability

This study did not generate new unique reagents.

Method details

Preparation of carboxy dye solutions

Carboxy dyes Atto 565 or Atto Rho3B (ATTO-TEC GmbH) were dissolved in dimethyl sulfoxide (DMSO) (Sigma Aldrich) and furthered diluted in MilliQ double distilled water (DDW) supplemented with 0.05 % (V/V) Tween 20 (Sigma Aldrich) to reduce nonspecific absorption to the surfaces. The concentrations of the dyes were measured using a UV-Vis spectrometer (Agilent technologies). The final sample concentrations were kept between 1 - 10 nM with a stoichiometric ratio as defined by Equation 1.

Protein labelling

NHS-ester conjugated Atto 565 or Atto Rho3B (ATTO-TEC GmbH) dyes were dissolved in DMSO as recommended by the manufacturer’s instructions. Recombinant OVA protein (Sigma Aldrich) was reconstituted in phosphate buffer saline (PBS, pH 7.4) containing 10% glycerol and frozen into aliquots. OVA samples were defrosted on ice and diluted in a freshly prepared and degassed reaction buffer, consisting of 130 mM NaCl, 2.5 mM KCl, 7.7 mM Na₂HPO₄⋅7H₂O, 1.7 mM KH₂PO₄ and 9.5 mM NaHCO₃, pH 8.35. The NHS-ester conjugated dyes Atto 565 and Atto Rho3B were added at different ratios to the OVA samples (further information is provided in the supplemental information) and the lysine residues of the protein were labeled overnight (O/N) at 25°C with shaking at 300 rpm. Subsequently, unconjugated dyes were removed using vivaspin concentrator (Cytiva) with a molecular cut-off of 30 kDa. The buffer was exchanged several times until no dye was observed in the flow through (typically 6-7 washes of 500 μl were required for complete removal of unconjugated dyes). The samples for the life-time measurements were prepared by diluting the protein labelled samples with 400 μM SDS (Bhuyan, 2010), 30 μM TCEP (Comasseto and Guarezemini, 2008) and 0.05% Tween 20 (Buschmann et al., 2007) in the reaction buffer for 30 min at 25°C with shaking at 300 rpm. The samples were heated at 90°C for 5 min and kept at 37°C prior to the experiments.

Experimental set-up

A schematic illustration of the TCSPC setup arrangement is shown in Figure 2A. The pulsed, 561 nm pico-second laser (D-TA 560B, PicoQuant) was operated at 10 MHz frequency. The laser beam was spatially filtered by feeding it through a single-mode polarization preserving optical fiber (Point source), and the collimated beam output was further expanded and steered to fill the back aperture of a 63x/1.15 NA water immersion objective (Zeiss). The emitted light was separated from the excitation using an appropriate dichroic mirror and focused onto a 50 μm pinhole located at the focal point of a 200 mm achromatic doublet lens (Thorlabs). The light was then filtered by a 562 nm notch and a 500 nm long pass filters (Semrock) and focused onto a low dark count single photon avalanche diode (SPAD) (PDM-100ct, MPD). The NIM output of the APD was used for superior timing resolution and was fed to the TimeHarp 200 or MultiHarp 150 acquisition hardware (PicoQuant). The sync pulse from the laser driver (PDL-800-D, PicoQuant) was connected through a 3 m long coaxial cable.

IRF analysis

The IRF is the instrument response function, that in general represents the temporal uncertainty introduced by the electronics while recording the arrival times of photons. A number of components contribute to the IRF, among them is the detector’s noise dominated by the conversion from a photon to an electrical signal, the light source (pulsed laser) producing light pulse jitter, and the counting electronics (Boas, 2007). Acquiring the IRF can be performed by two main methods, namely measurements of a scattering solution or using strongly quenched fluorophores that are known to exhibit very short lifetime values. The second approach is usually considered more accurate especially if the detectors temporal response demonstrates a spectral dependency (Boas, 2007). In this work we have performed IRF measurements using a highly diluted milk solution and also using the Allura red dye (Sigma , 25956-17-6) which has an emission spectrum range similar to the dyes used in the experiments (Chib et al., 2015), and lifetime of roughly 0.23 ns. The two lifetime measurements of the IRFs are nearly identical as shown in Figure S3A.

The measured IRF is characterized by fitting to an EMG distribution function defined by Equation 3 (Grushka, 1972), where $erfc\left(x\right)=\frac{2}{\sqrt{\pi }}\underset{x}{\overset{\infty }{\int }}{e}^{-t^2}dt$. The parameters obtained in this model can be used to create artificial times representative of the real IRF which is then used for the simulations.

$$f\left(x;\mu ,\sigma ,\tau \right)=\frac{1}{2\tau }{e}^{\frac{1}{2\tau }\cdot \left(2\mu +\frac{{\sigma }^2}{\tau }-2x\right)}\cdot erfc\left(\frac{2\mu +\frac{{\sigma }^2}{\tau }-2x}{\sqrt{2}\sigma }\right).$$ (Equation 3)

An example of the IRF fitting acquired from a scattering solution is presented in Figure S3B. Fitting the IRF data to an EMG distribution, yields the following parameters: μ=0.759±0.006, σ=0.137±0.006 (or a FWHM of 0.322 ns), τ=0.181±0.006 ns, χ²=0.112 ). Data acquired using a highly diluted milk solution.

Monte Carlo simulations and TCSPC data analysis

The Monte Carlo simulations were used to study the stochastic photon emission from a pure or a binary fluorophore mixtures. All simulations were performed using MATLAB (MathWorks) and the detailed code as well as all the variables’ definitions appear in the Supporting information. The fluorophores were modeled as ideal emitters obeying a single exponential lifetime decay function therefore the photon arrival times obeyed the exponential distribution functions:

$$\begin{array}{l}f\left(t\right)=\lambda \cdot \left(\frac{1}{1-e^{-\lambda \cdot T}}\right)\cdot e^{-\lambda \cdot t}\hfill \end{array}$$ (Equation 4)

$$f\left(t\right)=r\cdot {\lambda }_1\cdot \left(\frac{1}{1-e^{-{\lambda }_1\cdot T}}\right)\cdot e^{-{\lambda }_1\cdot t}+\left(1-r\right)\cdot {\lambda }_2\cdot \left(\frac{1}{1-e^{-{\lambda }_2\cdot T}}\right)\cdot e^{-{\lambda }_2\cdot t}$$ (Equation 5)

where λ_i=1/τ_i, τ_iis the lifetime of the two fluorophores, and T is the simulated time span interval examined, limited by 1/(laser pulse rate). Equation 4 represents a sample with a single component, while Equation 5 is modeling a sample containing a mixture of the two fluorophores where r represents the relative molar ratio.

The simulation starts with creating the desired amount of photon’s arrival times based on the exponential distributions Equations 4 or 5. The created arrival times are binned into time channels, hence creating a histogram in which the time constant is set by the hardware resolution (i.e., 0.0363 ns). The number of photons in each channel is referred to as the counts vector, which for simulating a more realistic behavior of the system is modified by the Instrument Response Function (IRF) and Poisson noise.

The IRF transforms the data set by convoluting the counts vector with the IRF vector, which can be the real IRF obtained from our system or an artificial IRF created based on an EMG (Exponential modified Gaussian) (Grushka, 1972) distribution function using parameters representative of a real IRF. The Poisson noise alters the counts vector according to a procedure described by Demas (DEMAS, 1983).

• a)
  If the number of photons in a single channel is less than 20 the Knuth algorithm (Knuth, 1997) is applied with the following steps:

  • 1.
    Initialize the variables:

$$\begin{array}{l}{N}_0=0,Q_0=1,P=e^{-\mu }\hfill \end{array}$$ (Equation 6)

μ is the original count number in the channel.

• 2.Generate a uniformly distributed variable U (using a random number generator) and start an iterative process, calculate:

$$\begin{array}{l}{Q}_{j+1}=Q_{j}U.\hfill \end{array}$$ (Equation 7)

• 3.If Q_j+1>P, then set:

$$\begin{array}{l}{N}_{j+1}=N_j+1\hfill \end{array}$$ (Equation 8)

and go back to step 2.

• 4.If Q_j+1<P the calculation is complete, and the final N obtained is the new counts number.

• b)In case the number of photons in larger than 20 the Gaussian distribution approximation can be applied (DEMAS, 1983):

$$\begin{array}{l}f\left(x\right)=\frac{1}{\sigma \sqrt{2\pi }}{e}^{-\frac{1}{2}{\left(\frac{x-\mu }{\sigma }\right)}^2}\hfill \end{array}$$ (Equation 9)

σ is the standard deviation taken as σ=1.

For the final counts vector , the MLE de-convolution fitting algorithm can be applied based on (Maus et al., 2001) work, which was developed for a single fluorophore specie and further expanded here for a mixture of two species. The algorithm follows the assumption that the counts number in the channels follows a Poisson distribution, therefore we wish to minimize the following expression:

$$\begin{array}{l}2I=c\cdot \sum _i^K{n}_i\text{ln}\frac{n_i}{g_i}\hfill \end{array}$$ (Equation 10)

where c is a numerical factor, generally written as: $\frac{2}{K-\nu }$ , when K is the overall channel’s number, which is determined by the hardware temporal resolution, ν is the number of degrees of freedom. Notably, however c is often simply assumed to be equal to 2 (Maus et al., 2001). n_i is the number of counts we have for a channel i, and g_i is the calculated number of photons from the fit. We obtain g_i from convoluting the IRF with the desired exponential distribution function:

$$\begin{array}{l}{g}_i=N_g\left[\lambda \cdot \left(\frac{1}{1-e^{-T\cdot \lambda }}\right)\cdot \frac{ir{f}_i\otimes e^{\frac{-\lambda \cdot i\cdot T}{k}}}{{\sum }_{i=0}^{K}ir{f}_i\otimes e^{\frac{-\lambda \cdot i\cdot T}{k}}}\right]\hfill \end{array}$$ (Equation 11)

$$g_i=N_g\left[r\cdot {\lambda }_1\cdot \left(\frac{1}{1-e^{-{\lambda }_1\cdot T}}\right)\cdot \frac{ir{f}_i\otimes e^{\frac{-{\lambda }_1\cdot i\cdot T}{K}}}{{\sum }_{i=0}^{K}ir{f}_i\otimes e^{\frac{-{\lambda }_1\cdot i\cdot T}{K}}}+\left(1-r\right)\cdot {\lambda }_2\cdot \left(\frac{1}{1-e^{-T\cdot {\lambda }_2}}\right)\frac{ir{f}_i\otimes e^{\frac{-{\lambda }_2\cdot i\cdot T}{K}}}{{\sum }_{i=0}^{K}ir{f}_i\otimes e^{\frac{-{\lambda }_2\cdot i\cdot T}{K}}}\right]$$ (Equation 12)

Equation 11 applies in the case of a single component, while Equation 12 applies for a binary component system. N_gis defined as the total number of counts from all channels, irf_i is the number of counts in channel i for the IRF. The discrete convolution between the components is calculate as follows:

$$ir{f}_i\otimes e^{\frac{-\lambda \cdot i\cdot T}{K}}=\sum _{j=1}^{i}ir{f}_j{e}^{-\left(i-j\right)\cdot \frac{\lambda \cdot T}{K}}+\sum _{j=i+1}^{K}ir{f}_j{e}^{-\left(i+K-j\right)\cdot \frac{\lambda \cdot T}{K}}.$$ (Equation 13)

We wish to estimate the parameters (r/τ) by a minimization process of I (Equation 10) performed by calculating g_i repeatedly while iterating over the fit parameter (r/τ).

The same minimization process is performed for a counts vector acquired from real TCSPC data, obtained from experiments on samples with a single fluorophore specie or a binary mixture.

Published: January 21, 2022

Data and code availability

All original code is available in this paper’s supplemental information.

All data reported in this paper will be shared by the lead contact upon request.

Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.