A support tool for planning classrooms considering social distancing between students

Abstract

In this paper, we present the online tool http://salaplanejada.unifesp.br, developed to assist the layout planning of classrooms considering the social distancing in the context of the COVID-19 pandemic. We address both the fixed and non-fixed position seat allocation problems. For the first case, we use two integer optimization models and discuss some curiosities about the solutions found. For the case that the seats can be moved freely, we handle the problem with circle packing techniques using continuous non-linear optimization. For these instances, we propose new algorithms, following other packing problems approaches in the literature. In addition, we propose a fast heuristic that provides a good starting point for the optimization procedure and also an efficient configuration ensuring the students positions in lines, which may be of interest to the user. Computational results are presented to illustrate the numerical behavior of the algorithms and models.

Introduction

In the context of COVID-19, social distancing has been one of the main strategies to stop the advance of the pandemic. After an initial moment of stricter confinement, daily activities gradually returned and protocols of distancing were inserted in several of them. In view of this situation, it was possible to see on a daily basis occasions where the decision-maker chooses configurations of seats which do not comply with the minimum distance recommendations or do not produce the best possible use of space. In fact, this was an expected circumstance, as it involved many people without technical training and/or advice to deal with this type of problem.

In May 2020, we realized that we could collaborate with the planning of the return of in person activities, developing a free web application to assist this planning. We decided to focus our efforts in the back to school context, which requires careful planning from educational managers and was, at the time, under heavy discussion in part of Brazil. Clearly, among the measures adopted to reduce the spread of the virus in a classroom is the space between desks. In an effort to quickly meet demand, we set up an interdisciplinary working group to address the problem and within a month we had the first versions of the algorithms. At the end of July 2020, we made available a free online tool called “Planned Room”, at http://salaplanejada.unifesp.br. Since then our tool has had accesses from more than 30 countries and was used to assist in planning the return to face-to-face educational activities by various educational institutions, companies and also by government education departments.

There are some works considering social distancing in recent literature. The allocation of seats on airplanes is considered in (Ghorbani et al. 2021; Salari et al. 2020). Scientific blogs (Lustig 2020; Jackson 2020) discuss how to determine seats in sports stadiums. In these situations, there is a finite amount of possibilities for allocating seats, and the decision-maker aims to define which ones should be occupied. Other applications with social and economic relevance, such as determining seating in movie theaters, restaurants and waiting rooms, could benefit from this type of approach.

Mixed-integer optimization problems based on dispersion models are commonly used for this purpose. Namely, the problem of allocating p people as far away as possible is known as the discrete p-dispersion problem. On the other hand, the problem of determining how many students fit in a classroom while respecting the minimum distance is an instance of the so called d-separation problem. In Kudela (2020), social distancing was modeled as a p-dispersion mixed-integer linear optimization problem, which was recursively solved using recent techniques. Problems up to 30 individuals and some convex and non-convex rooms were considered. The same model was applied in Murray (2020), but considering that the seats are fixed, as it is observed in classrooms and theaters, for example. The p-dispersion and d-separation approaches were discussed. A commercial solver was used to solve the classical models, but only one room was studied for the p-dispersion model. According to Erkut (1990), since the maximal clique problem in graph theory could be solved as both problems, they are known to be NP-complete (Garey and Johnson 1990). Due to the different applications of the problem and all its theoretical challenges, several works have been published on these themes, see for example, (Contardo 2020; Erkut et al. 1996; Sayah and Irnich 2017).

If seats are allowed to move freely the problem of maximizing the distance between students can be seen as a problem of obtaining the maximum distance between points within a given region, most often a rectangle. As shown in Goldberg (1970), this problem is closely related to the circle packing problem, whose literature is quite vast, as shown by the review proposed by Hifi and M’Hallah (2009). In Ugail et al. (2021), the design of physical spaces considering social distancing is solved by circle and ellipsis packing problems. Nonconvex non-linear programming problems are suggested and solved by interior point methods available in a proprietary software. The models are able to address any room given by convex functions, considering fixed or moving tables and also the air flow. No software or code is easily available to the user.

Circle packing problems are usually addressed by non-linear optimization (Birgin and Gentil 2010), mixed-integer optimization (Torres-Escobar et al. 2018) or geometric and general heuristics (Morinaga et al. 2014). The problem of packing as many circles as possible inside fixed rectangles is usually solved by heuristics (Birgin et al. 2005; Dowsland 1991; Isermann 1991) or by integer programming (Litvinchev and Espinosa 2014; Litvinchev et al. 2015). Recently, ellipsis packing problems have been solved by non-linear programming in (Birgin and Lobato 2019; Pankratov et al. 2018).

As we observe, social distancing in rooms usually is based on the use of classical models and techniques. The exception is Kudela (2020), which implements new strategies to solve larger p-dispersion problems. Unfortunately, none of the above mentioned works easily provide their tools to a non-expert audience. “Planned Room”, on the other hand, was created to be free, simple, easy to use and deliver fast and good solutions, to achieve social distancing in classrooms. Behind the web application, a more complex but also more powerful and complete open source software is executed, coupled with a database of already computed problems. In this work, we present the theoretical and practical aspects of the tool.

We consider that the social distancing is modeled by different approaches, allowing the user to select what kind of model will be used. The tool allows maximizing the number of students or the distance between them for a given number of students, in addition to consider whether the seats are fixed or not. The case with fixed seats and maximizing the number of students is modeled as a d-separation problem whereas maximizing the distance between students as a p-dispersion problem, in a similar way as Kudela (2020) and Murray (2020), respectively. When handling the layout with free seats non-linear programming models for circle packing problems are used, as in Ugail et al. (2021), but with an efficient implementation and a novel heuristic to improve the speed and also provide layouts “in rows”, which are specially suitable for classrooms. Our tool is based on well-established implementations for circle packing problems using Algencan (Martínez and Birgin 2020) software. However, we introduce a truncated penalty strategy to identify good solution candidates, speeding up the process.

The simplicity of the tool allows decision-makers to perform several simulations. The Application Programming Interface (API) that is also provided by the tool, permits integration with other applications. Throughout the API, “Planned Room” is being used by the Brazilian largest national high school exam (ENEM), which gives access to several universities in Brazil, to simulate and implement social distancing for more than 130,000 classrooms. By the end of July 2021, the tool has provided planning for more than 500,000 rooms.

The rest of this work is organized as follows. In Sect.  2, we present the mathematical models used to solve the problems when the seats are fixed and discuss some curiosities about the results obtained. In Sect. 3, we present the non-linear optimization modeling, the proposed algorithm to solve it and the implementation details for computational efficiency. In Sect. 4, we present the proposed heuristic and discuss some results when it is used as the starting point of the optimization algorithm and when it is used to generate solutions by rows. A detailed discussion about the tool is presented in Sect. 5 and final remarks are given in Sect. 6.

The fixed seats problem

In this section, we consider the problem of allocating students to a room which all seats are fixed. On a daily basis, establishment managers usually allocate people by interleaving seats, as in a chessboard pattern. Several times, this solution either is sub-optimal or clearly does not follow the minimum distance requirements indicated by health authorities. In these cases, the configuration which better takes advantage of the available seats is not always straightforward. As already mentioned, the problem of maximizing the number of seats without changing their configuration can be modeled as a d-separation problem and solved by off-the-shelf mathematical programming tools.

Let n be the number of available seats on the room map and $d_{\mathit{ij}}$ be the distance between seats i and j, obtained by a distance matrix. Also, let $x_i$, $i=1,\cdots ,n$, be a binary variable that indicates whether the i-th seat should be occupied or not. Thus, the aim is to maximize the number of occupied seats, given by $\sum _{i=1}^n{x}_i$, respecting that two seats cannot be simultaneously occupied if the distance between them is less than $d_{\mathit{min}}$, the minimum required distance. The situation can be modeled as the following binary programming problem:

$$\begin{array}{c}\hfill \begin{array}{cc}\text{max}\hfill & \sum _{i=1}^n{x}_i\hfill \\ \text{s.}\text{t.}\hfill & x_i+x_j\le 1,\forall i,j\in \{1,\cdots ,n\}:i<j,d_{\mathit{ij}}\le d_{\mathit{min}}\hfill \\ \hfill & x_i\in \{0,1\},\forall i\in \{1,\cdots ,n\}.\hfill \end{array}\end{array}$$ 1

Other models for the d-separation problem, also called r-separation problem or anti-cover problem, are shown in (Moon and Chaudhry 1984; Erkut et al. 1996; Church and Murray 2018). In these works, the authors present formulations with tighter linear relaxations and/or reducing the number of constraints. With these strategies, the computational time to solve the problem is significantly reduced. On the other hand, the use of such techniques requires the implementation of considerably more complex problem-specific solvers, while our focus is to use free, well-established solvers.

We now consider the problem of allocating a fixed amount of students, denoted by p, so that they are as far from each other as possible. This type of problem is known as the p-dispersion problem and has many applications when the allocation points do not necessarily represent a place but a list of attributes, so that one wants to choose the most heterogeneous group possible (Erkut 1990). Unlike the d-separation problem, the most common formulations of the p-dispersion problem are non-linear. We use a well known mixed-integer linear model that, again, can be solved by off-the-shelf optimization tools. Many authors suggest solving this linear approach instead of applying advanced strategies to its non-linear version. See Kudela (2020), for more details.

Let $x_i$ and $d_{\mathit{ij}}$ be the same as in (1). Also let d be the variable that represents the shortest distance between two occupied seats and M a big number, greater than or equal to the largest distance between two seats in the room. The allocation of the p students in the room, maximizing the minimum distance between them is given by the following model:

$$\begin{array}{c}\hfill \begin{array}{cc}\text{max}\hfill & d\hfill \\ \text{s.}\text{t.}\hfill & d\le M(2-x_i-x_j)+d_{\mathit{ij}},\forall i,j\in \{1,\cdots ,n\}:i<j\hfill \\ \hfill & \sum _{i=1}^n{x}_i=p,\hfill \\ \hfill & d\in \mathbb{R},x_i\in \{0,1\},\forall i\in \{1,\cdots ,n\},\hfill \end{array}\end{array}$$ 2

where the first group of constraints guarantee that $d\le d_{\mathit{ij}}$ is enforced only if seats i and j are occupied.

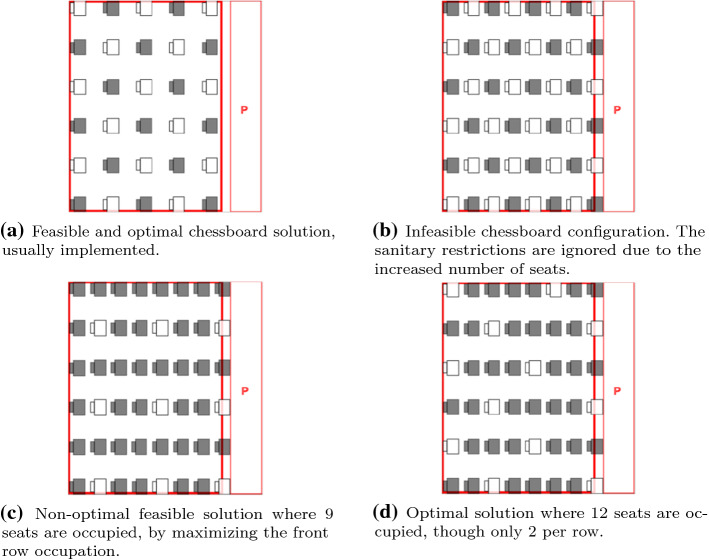
The optimization problems related to the student’s allocation considering fixed seats are solved using Google OR-Tools (Google 2020). The OR-Tools package, developed by Google, uses the Coin CBC algorithm, which is a Branch-and-Cut solver written in C++. The processing time to solve the instances received on the website was relatively short, meeting users’ expectations for an online tool. For example, using the Federal University of São Paulo (UNIFESP) server1 it takes, on average, about 0.01 seconds to solve problem (1), defined by a $5m\times 7m$ room, with 6 rows of 5 seats each, uniformly distributed $0.5m\times 0.5m$ sized seats and minimum distance of 1.5m, whose solution is shown in Fig. 1a. In the figure, white seats represent occupied seats and the “P” space is reserved to the teacher (not included in the $5\times 7$ size of the room). A more complete description of the tool is given in Sect. 5. Bearing in mind that the answer is immediate when the problem is already stored in the database, we believe that it would not be necessary to dedicate greater efforts to build a better model.

Fig. 1.

Three feasible solutions (a,c,d) and one infeasible configuration (b) for the problem defined by a $5m\times 7m$ room with $0.5m\times 0.5m$ seats and a minimum distance of $1.5m$. White seats represent occupied seats and “P” is the space reserved to the teacher. Here, increasing the number of seats may reduce the number of occupied seats

To illustrate an interesting situation, let us return to the problem of maximizing the number of occupied seats, using model (1), in the classroom described in the previous paragraph. The solution presented in Fig. 1a is the usually employed chessboard configuration. If, under the same settings, we increase the number of chairs in each row to 8 instead of 5, interleaving the occupied seats, as shown in Fig. 1b, is not a feasible configuration anymore, since there would be occupied seats whose distance between them is 1.36m. It is not uncommon to see this type of solution implemented in practical situations. Another type of solution usually implemented in these situations is to skip the minimum number of seats in the row so that the minimum distance is respected. However, this strategy can prevent the use of neighboring rows if we are committed to respect sanitary restrictions, as illustrated in Fig. 1c. Finally, the solution found by our tool is shown in Fig. 1d.

Looking at Figure 1, we notice an interesting situation in which, by increasing the number of seats in the room from 30 to 48, the maximum number of students drops from 15 to 12. Moreover, an increase of 3 seats (i.e. a third of the total) in the optimal solution compared with a common sense strategy, shows the importance of a tool such as the one proposed here. For example, a group of 48 students could rotate every 4 classes adopting the optimal solution, but using only 9 places in the room, the rotation would have to be every 6 meetings if we consider fixed groups. This represents a 50% increase in the number of face-to-face classes that each student would have throughout the year.

When solving model (2), we observed that the processing times were, on average, 50 times higher than solving (1). In this case, an important question would be whether the configuration obtained by maximizing the number of students in the room using (1) also guarantees a good dispersion between them. To verify this, we consider 4000 valid fixed-seat configurations that we had in our database on July 21, 2021. For this collection of problems, we obtain p as a solution to (1) and use this value as input to solve (2). In 84% of the cases, the distance found by solving (1) was also found by (2) (ignoring differences smaller than 1cm), indicating a good dispersion obtained in (1) and, therefore, in practical situations, there would be no need to re-optimize after obtaining the maximum capacity of a room. In addition, according to Sun and Zhai (2020), the probability of exposure to the virus decreases logarithmically as the distance increases, following the relation $P(d)=(-18.19ln(d)+43.226)/100$. If $d=1.5$, then a 1 cm perturbation changes the probability by only $0.1\%$. The larger the required social distancing is, the smaller is such change in the probability.

The free positioning problem

In this section, we consider the case where N seats can move freely in a rectangular room. We start by developing strategies to solve the social distancing problem for a given number N of seats, which is detailed in Sects 3.1 and 3.2. In Sect. 3.3, we describe how to extend the algorithms to solve the problem of finding the maximum number N of seats in a rectangular room.

Truncated penalization strategy

Let us address the problem of allocating N students within a classroom so that they are as separate as possible, considering now that each seat can move freely in the room. In this work, this problem is modeled as the packing of N identical circles in a rectangular container. The position of each student corresponds to the center of a circle whose coordinates are denoted by $(c_i^x,c_i^y)$, $i=1,\cdots ,N$, and must be contained in a rectangle determined by the dimensions of the room, reduced by half the width of a seat on each side and half the length of a seat at the bottom. The top of the room is not reduced, since we assume that the space of the teacher has already been considered and, therefore, is not a physical barrier. See Sect. 5 for more information about the hypotheses assumed for the tool.

We will denote the width and length of the rectangle actually considered in the problem by h and b, respectively, and, without loss of generality, we assume that it is placed in the first quadrant with its lower left vertex at the origin. Also, we denote $d_{\mathit{min}}$ as the maximum between the radius of the smallest circle containing the seat and the social distancing required by authorities. Let d be the variable associated with the smallest distance between seats. The problem of interest can be modeled as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}\text{min}\hfill & -d\hfill \\ \text{s.}\text{t.}\hfill & {(c_i^x-c_j^x)}^2+{(c_i^y-c_j^y)}^2\ge d^2,\hfill & \forall i,j\in \{1,\cdots ,N\}:j>i,\hfill \\ \hfill & 0\le c_i^x\le b,0\le c_i^y\le h,\hfill & \forall i\in \{1,\cdots ,N\},\hfill \\ \hfill & d_{\mathit{min}}\le d.\hfill \end{array}\end{array}$$ 3

The first group of constraints states that the Euclidean distance between two seats is at least d. They are usually denoted as “non-overlapping constraints”. The second group ensures that seats are inside the room. The third constraint is just a technical constraint to avoid uninteresting values of d.

Problem (3) is a well-known non-linear optimization approach to circle packing (Birgin et al. 2005; Birgin and Sobral 2008; Birgin and Gentil 2010), recently used in Ugail et al. (2021) under the COVID-19 context. It is a particular case of general non-linear programming problems, usually written in the following format:

$$\begin{array}{c}\hfill \begin{array}{cc}\underset{x\in \Omega }{\text{min}}\hfill & f(x)\hfill \\ \text{s.}\text{t.}\hfill & h(x)=0,g(x)\le 0,\hfill \end{array}\end{array}$$ 4

where $\Omega$ is given by the so-called lower level constraints, for example an n-dimensional box, which can be easily treated by optimization algorithms and $f:{\mathbb{R}}^n\to \mathbb{R}$, $h:{\mathbb{R}}^n\to {\mathbb{R}}^m,g:{\mathbb{R}}^n\to {\mathbb{R}}^p$ have continuous first derivatives on ${\mathbb{R}}^n$.

A well-established method to solve this type of problem, especially when the number of constraints is large, as could be the non-overlapping constraints, is the Augmented Lagrangian method. A comprehensive review can be found in Birgin and Martínez (2014). This type of method can be seen as a shifted penalization method, where the shifts are defined by estimates of the Lagrange multipliers. More precisely, for fixed values of multiplier estimates ${\lambda }^k$ and ${\mu }^k$, associated with constraints h and g, respectively, and a penalty parameter ${\rho }_k$, at iteration k the function

$$\begin{array}{c}\hfill \mathcal{L}(x,{\lambda }^k,{\mu }^k,{\rho }_k)=f(x)+\frac{{\rho }_k}{2}{∥h,(x),+,\frac{{\lambda }^k}{{\rho }_k}∥}_2^2+\frac{{\rho }_k}{2}{∥{\left(g,(x),+,\frac{{\mu }^k}{{\rho }_k}\right)}_{+}∥}_2^2\end{array}$$ 5

is minimized subject to $x\in \Omega$. Afterwards, ${\lambda }^k$, ${\mu }^k$ and ${\rho }_k$ are updated and a new external iteration is started.

Algencan (Andreani et al. 2008; Martínez and Birgin 2020) is a solver based on this type of method, that uses Gencan (Birgin and Martínez 2002) to solve the subproblems, employing Newtonian techniques, spectral projected gradients and active-set strategies. Algencan and Gencan have successfully solved non-linear programming problems associated with packing circles in rectangles (Birgin et al. 2005; Birgin and Sobral 2008; Birgin and Gentil 2010) and several other packing problems in more general contexts (Martínez et al. 2009; Birgin et al. 2013; Birgin and Lobato 2019). For this reason, they were chosen to solve the non-linear optimization problems used in the present tool.

Problem (3) has $n=2N+1$ variables, $p=N(N-1)/2$ inequality constraints (the non-overlapping constraints), $m=0$ equality constraints and $\Omega =\{(c,d)=((c_1^x,c_1^y),\cdots ,(c_N^x,c_N^y),d)\mid 0\le c_i^x\le b\text{and}0\le c_i^y\le h,i=1,\cdots ,N\}$. Birgin and Sobral (2008) proposed to group the non-overlapping constraints into the following single constraint

$$\begin{array}{c}\hfill \overline{h}(c,d)\equiv \frac{1}{2}\sum _{i=1}^{N-1}\sum _{j=i+1}^{N}max{\{d^2-{(c_i^x-c_j^x)}^2-{(c_i^y-c_j^y)}^2,0\}}^2=0.\end{array}$$ 6

This approach allows a complexity reduction from $O(N^2)$ to O(N) when calculating non-overlapping constraints and their gradients. To do this, it is necessary to construct a mesh of width d in the plane, then map each center $(c_i^x,c_i^y)$ to a position in this mesh and verify whether $(c_i^x,c_i^y)$ and $(c_j^x,c_j^y)$ belong or not to neighboring positions. If they are not neighbors, then we skip their associated term in (6). In practice, we only need to construct the mesh around the room. Since $d\ge d_{\mathit{min}}$, a matrix can be previously allocated to represent the mesh. At each entry, a linked list is used to efficiently store items and locate neighbors, which also allows for a fast computation of (6) that increases linearly with N. In Birgin and Sobral (2008), the value of d is fixed, but for our application we adapt it for a variable d. This does not result in loss of efficiency, since the mesh is never explicitly constructed and the mapping procedure has to be run every time $\overline{h}$ has to be evaluated.

In Birgin and Gentil (2010), it is reported that an earlier version of Algencan had difficulties in finding very precise solutions using the formulation of the non-overlap constraints given by (6). In Bueno et al. (2019), it is argued that this difficulty may be associated with an increase in the non-linearity inherent in the reformulation. In addition, the gradient of (6) is null at any feasible point, which shows a lack of regularity in the constraint and may imply worse convergence rates of computational methods. In the context of this work, we are not concerned with highly accurate solutions, since there is no need to consider decimal places beyond centimeters to place a seat. Anyway, concerned with the strong non-linearity and the non-regularity imposed by the use of (6), we propose a strategy to accelerate the computational performance.

Let us see what happens if we apply the Augmented Lagrangian method to solve problem (3). Denoting $x=(c,d)$, using null Lagrange multipliers, an initial penalty parameter ${\rho }_0$ and the function $\overline{h}$ defined in (6), the objective function of the subproblems would be given by

$$\begin{array}{c}\hfill \mathcal{L}((c,d),0,{\rho }_0)=-d+{\rho }_0\overline{h}(c,d).\end{array}$$ 7

In this way, we can use Gencan to solve the subproblem while still taking advantage of the fast strategy adapted from Birgin and Sobral (2008). Unfortunately, once we have the introduction of the Lagrange multipliers, there would be different shifts for each one of the non-overlapping constraints and so the use of the fast evaluation strategy would not be so immediate. For this reason, it is not straightforward to complete the entire optimization process with Algencan using model (3) if we want to take advantage of the structure from Birgin and Sobral (2008) .

On the other hand, as increasing the radii of the circles is associated with leaving their centers as far apart as possible, in a certain way the objective function (7) is not entirely in conflict with the non-overlapping constraints. Hence, we hope that the centers obtained by minimizing $\mathcal{L}((c,d),0,{\rho }_0)$ over $\Omega$ can be very good approximations of the solutions of the original problem, even if relatively low penalty parameters are used. Once the values of c are found, we can define the value of d as being the smallest distance between two different centers, which is more reliable than the value obtained by the optimization. Since this procedure is equivalent to performing only one iteration of the Augmented Lagrangian method to find c, we use this strategy, which we call the truncated penalization strategy, to estimate promising solutions.

Multi-start strategy

Packing problems have several non-global local minima and infeasible stationary points, so it is usual to apply a multi-start strategy in the search for a good solution. In our implementation, instead of the traditional approach of generating random centers inside the room, we create random perturbations of a feasible solution returned by the heuristic procedure described in Sect. 4. As we show in Sect. 4, the heuristic generates high quality initial guesses with very low computational effort. The perturbation strategy is coupled with the truncated penalization strategy described before to form the basis of the multi-start algorithm for the free-layout problem, which is given by Algorithm 1 and discussed in the next paragraphs.

In Algorithm 1, ntrials is the number of trials that will be used by the truncated strategy, to find promising solutions, which are stored in set S. The optimization processes at steps 4 and 7 of Algorithm 1 use different stopping criteria. At Step 4, we require a loose tolerance when calling Gencan (epsfeas and epsopt, the feasibility and optimality tolerances, respectively, are set to 0.01 and the number of iterations is limited to 2000, more details on those parameters see Birgin and Martínez (2014)). We select at most $S_{\mathit{max}}$ most promising feasible solutions and only for these we complete the process more accurately, at Steps 6 and 7. To refine the solution, at Step 7 we use Algencan with tolerances epsfeas and epsopt set to ${10}^{-8}$.

To clarify the gain in using the strategy of selecting promising points by minimizing (7) in $\Omega$, we compared the results obtained against running only Algencan with the same tolerances of Step 7 and the same starting points. We generated an artificial set of 87 problems by considering valid combinations of the problem’s parameters: $b\in \{7,12,20\}$, $h=t·b$ for $t\in \{0.2,0.4,0.5,0.6,0.8,1\}$ and $N\in \{5,10,15,20,30,50,100\}$. All the possible combinations generate 126 problems. By asking for 1.5m as the minimum distance, only 87 of them are actually feasible. We considered $\mathrm{ntrials}=100$ for both strategies and limited |S| to a maximum of $S_{\mathit{max}}=5$ for Algorithm 1. The average CPU time per successful trial (one that produces a feasible solution) was reduced by 75% when the truncated penalized strategy was used, while only in 2 small instances (with $N=15$) the distances obtained differ by more than 1 cm.

Extension to maximizing the number of seats

Let us now consider the case where the user wants to maximize N, the number of seats. This problem can be seen as a problem of inserting the maximum number of circles of the same radius (defined by the minimum distance) in a rectangle. This problem was addressed in Birgin et al. (2005), where the authors start from $N=1$ and increase the value of N, whenever the resolution of the packing problem is successful. When it is not possible to solve the packing problem for a certain value of N, using a pre-fixed amount of starting points, the previous value of N is indicated as a solution. To solve the packing problem with each fixed N value, the authors use Gencan to minimize the function $\overline{h}(c,d_{\mathit{min}})$, where constant $d_{\mathit{min}}$ is the same as before and the centers given by c must belong to the rectangular container. In other words, this is exactly our strategy to find promising points described in Sect. 3.1, if we consider d as constant.

To search for the maximum value of N, we follow closely the strategy used in Birgin et al. (2005), but starting from a lower bound and limited by an upper bound. The lower bound is obtained by organizing the circles so that their centers form a mesh of square elements, that is, $\left(\lfloor ,b,/,d_{\mathit{min}},\rfloor ,+,1\right)\left(\lfloor ,h,/,d_{\mathit{min}},\rfloor ,+,1\right)$. By dividing the enlarged area of the room with the area of a circle with minimum radius we determine an upper bound for N, given by $\lceil (b+d_{\mathit{min}}/2)(h+d_{\mathit{min}})/(\pi {(d_{\mathit{min}}/2)}^2)\rceil$. Motivated by the intuition that distancing the circles leads to no overlapping, we use the truncated penalization strategy with fixed N to obtain the position of the circles. After that, we check if the shortest distance between the centers is greater than or equal to $d_{\mathit{min}}$ to decide if the problem was successfully solved. If the answer is positive, we increment N, otherwise we use a new starting point to try to solve the problem, until a limit of ntrials attempts (the same of Algorithm 1). If none of the starting points is successful, then the previous value of N is declared as the solution. Once N is obtained, we apply Algorithm 1 to obtain the configuration where the N students are as far apart as possible.

We compared this strategy against a bisection search strategy, where at each iteration the search interval of N is reduced by 2. Although the number of problems solved by the bisection strategy is smaller, we observed that the number of problems with values of N higher than the solution is larger. For such problems, Gencan takes much more CPU time than for solving problems with small N. As observed in Birgin and Lobato (2010), if N is the maximum number of students, the time for packing all problems from 1 up to $N-1$ is much smaller that solving one packing problem for values greater or equal than N. In our experiments, we used the same artificial set as before, but without setting N, resulting in only 18 problems. The bisection strategy takes, on average, twice the time to find the best value of N than the strategy described in Birgin et al. (2005) and used in this work.

A geometric heuristic

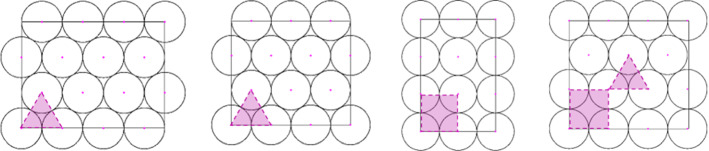
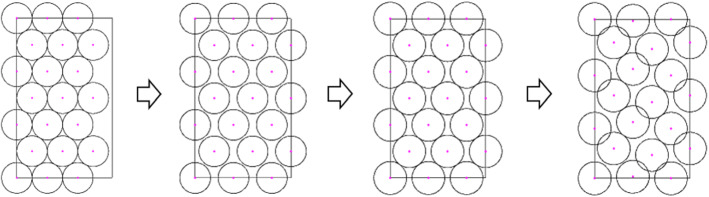
In this section, we propose a heuristic based on geometric arguments with low computational cost, which can be used to generate starting points for the multi-start strategy described in the previous section. It also can be used to quickly generate feasible solutions in rows, if seats can move freely in the room. The ideas were developed by associating the allocation problem with the problem of packing circles in rectangles. First, N points, representing the center of N circles, are distributed in the room, following several patterns. Then, the radius is computed, such that the circles are inside the rectangle and do not overlap. The pattern that provides the largest radius is returned. The heuristic is given by Algorithm 2 and its steps are fully detailed in this section.

The heuristic begins by creating several patterns by distributing the points as vertices of equilateral triangles and/or squares, as shown in Fig. 2. The distribution of points as vertices of an equilateral triangle gives us the best fill rate in a plane (Tóth 1953). On the other hand, the square-based format appears in optimal solutions in some cases, for example, when packing 9 circles in a unitary square (Schaer 1965). The patterns that result in circles with larger radius are considered as promising configurations for the next processes described latter in this section.

Fig. 2.

From left to right, distributions examples of Z, X, I and D-type patterns. In the Z and X patterns, the points are placed as vertices of an equilateral triangles. In the I-type pattern, the points are organized as vertices of squares. In D-type, there are two parallel rows such as in the I-type pattern and the other rows are organized as the X-type pattern

Using the nomenclature proposed by Dowsland (1991), we will divide the equilateral triangle pattern into two sub-patterns, Z-type and X-type. When the rows always have the same amount of points, organized in “zig-zag” lines, we call it Z-type pattern and when the number of points alternates, the even lines having one point less that the odd ones, we call it X-type pattern. Also following Dowsland (1991), the pattern in which the points are organized as vertices of squares is called I-type pattern. Here we introduce a new hybrid pattern, called D-type, which uses two parallel rows of I-type and is then followed by the X-type pattern. The idea is that, in this configuration, we could place one more circle than in the X-type pattern, at the cost of increasing the difference between the side of the square and the height of the equilateral triangle with the same edge. Note that combining types Z and I would not result in benefits, as we would not be able to insert a new circle. The patterns are shown in Fig. 2.

The rows in each pattern can be organized horizontally or vertically. However, the I-type pattern does not change substantially when considering different orientations. Thus, we consider seven possible patterns: two orientations for Z-, X- and D-type patterns, whereas the I-type pattern always follows the horizontal orientation.

Given a pattern, we have to determine the number f of lines to be built and the number q of elements in the first line to calculate the maximum possible radius. We do this by generating, in each pattern, all possible values of f and, for each value of f, its respective value of q and the maximum radius to accommodate at least N circles. In the cases where the number of points is large, we can estimate an interval that contains promising values of f, so that the distribution fill an rectangular area with sides ratio close to the proportion between the sides of the room. One possible way of estimating such interval is considering $f\approx \sqrt{\frac{\mathit{Nh}}{b}}$ if considering an I-type pattern and $f\approx \sqrt{\frac{2Nh}{\sqrt{3}b}}$ or $f\approx \sqrt{\frac{2Nb}{\sqrt{3}h}}$ for the other patterns, whenever they are horizontal or vertical. Figure 3 illustrates all the seven patterns for the distribution of 20 points in a $10\times 6$ rectangle. For each one of them, we report the configuration associated with the value of f, and the corresponding q, that results in the best radius.

Fig. 3.

The seven initial patterns generated to distribute 20 points in a $10\times 6$ rectangle. From left to right, Z-type and X-type patterns, each one with their respective orientations, followed by I-type with horizontal orientation and D-type with also two orientations. The respective best distances for each pattern are 1.9245, 2.2222, 2, 2, 2, 2 and 2

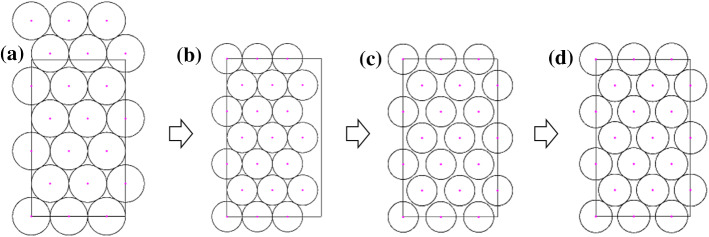
By fixing a pattern p and the number of lines f, we can compute q, denoted by $q_f^p$, as shown in Step 1 of Algorithm 2. Then, it is possible to calculate the maximum possible distance $d_f^p$ of the points so that they fill one side of the rectangle. This is performed by Step 2 of Algorithm 2. Using $d_f^p$ and f, we calculate the height of the triangles and squares to check if any point would be left out the rectangular region. If this happens, as shown in step a) of Fig. 4, the algorithm resizes $d_f^p$, ensuring that the last row would be internal to the rectangle, as shown in step b) of Fig. 4. After that, a spacing towards the region of the rectangle that is not yet occupied is considered, as we can see in step c) of Fig. 4. In some cases, this spacing can result in an increase in the $d_f^p$ value, as shown in d) of Fig. 4. This process is described by Step 3 of Algorithm 2. We observe that the resizing in the else part of Step 3 is such that all the steps of Fig. 4 are performed at once.

Fig. 4.

An example of the steps for adjusting and spacing the points in a Z-type horizontal pattern with $f=7$ and $q=3$

An interesting issue is that different patterns can generate the same final result after the adjustment and spacing procedures. In Fig. 5, we can see the same configuration generated in step d) of Fig. 4 considering now the X-type pattern with $q=4$ (alternating between 4 and 3 points) and $f=6$.

Fig. 5.

For 21 points and using the same rectangle, a Z-type pattern with $f=7$ and $q=3$ generates the same configuration of a X-type pattern with $f=6$ and $q=4$, after the adjustment and spacing procedures

There are also cases of patterns where, after being spaced out, some circles remain tangent to each other, and no improvement in $d_f^p$ is possible. I-type and D-type patterns are examples in which this fact always happens, as we can see in Fig. 6. This also occurs in other patterns, when $d_f^p$ is not updated in Step 3 of Algorithm 2. However, in Step 4 when the coordinates are calculated, the heuristic still performs the spacing processes in all cases, resulting in a more uniform distribution across the rectangle.

Fig. 6.

When the circles do not lose the points of tangency after spacing, there is no improvement in the distance value

So, in Step 4, using only the information of the pattern p, f, and $q_f^p$, the coordinates can be constructed by a loop that places the first point at one of the vertexes of the rectangle and follows increasing horizontal and vertical spacing values, which can be calculated considering the number of elements in each line and the dimensions of the rectangle. This process allows the coordinates to be generated only for the best distance value found or for the best values of each pattern. In fact, $d_f^p$ could even be computed using this approach, although some of the geometric motivation is lost in this case.

The solutions found by Algorithm 2 are always given in (horizontal or vertical) rows, which is a very welcome pattern to implement in practice. The tool offers the possibility to sacrifice optimality in exchange to quickly obtain solutions in rows, as discussed in Sect. 5. Usually the configuration obtained by the heuristic is very good, but it can be improved using the optimization process described in Sect. 3, as shown in Fig. 10. In this way, it is natural to consider the layout that resulted in the largest distance as a starting point of the optimization process. Similarly, in Stoyan and Yaskov (2012), triangular lattice configurations are used to build a good starting point for the optimization process. However, the inherent symmetries of the heuristic layout generate some stationarity for the optimization algorithm. Therefore, it is necessary to perturb the generated layout to be used as a starting point. We propose a perturbation strategy that also takes geometric aspects into account to obtain more chances of success, which is given by Algorithm 3.

Fig. 10.

Results for a $6m\times 8m$ room with $0.5m\times 0.5m$ desks and minimum distance of 1.5m between desks. We can see that the “non-row” positioning solution (b) is harder to implement, but it offers a 5cm increase in distancing over the solution obtained by rows (a)

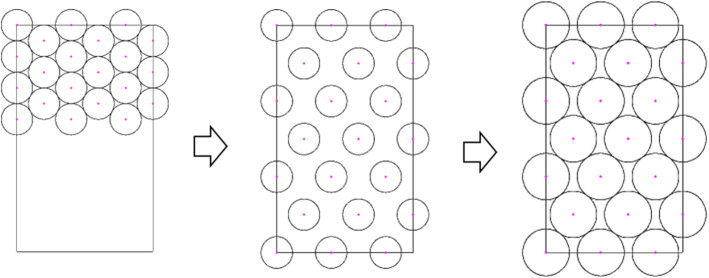
In horizontally-oriented patterns, Algorithm 3 adds or subtracts a uniformly generated random fraction of the distance $d_f^p$ to the y coordinate of some points. The idea is based on the algorithm being more likely to make better use of the space by avoiding the row formation and reorganizing the points. In this way, we alternate in each row which points should be moved up or down. To do this, we enumerate the circles from left to right in each line and across the lines. The fraction that defines the quantity to be added or subtracted in the y coordinate of the points is associated with a perturbation factor Q. For the even points in the first row, we add $d_f^p\xi Q/2$, where $\xi$ follows the uniform distribution in [0, 1] and is computed for each perturbation. Thus, some of the points in the first row are moved to the interior of the rectangle. Something similar is done in the last row, moving down half of the points by subtracting the y coordinates by $d_f^p\xi Q/2$. For the remaining points, which are not in the first or last lines, their y coordinates are changed by adding to the even points or subtracting from the odd ones, the value of $d_f^p\xi Q$. Figure 7 illustrates the process of obtaining the starting point used by the optimization algorithm described in Sect. 3. Namely, starting with a pattern that uses the entire height of the rectangle, first the circles are spread horizontally, then the radius is enlarged and finally the perturbation is done. For vertically constructed patterns the process is analogous, perturbing the x coordinate instead.

Fig. 7.

From left to right we start with a pattern that uses the entire height of the rectangle, so the circles are spread horizontally, then the radius is enlarged and finally the perturbation is done

To clarify the gain in using random perturbations of a heuristic promising point against pure random points, we use the same artificial set from Sect. 3. Again, the minimum distance was fixed as 1.5. The only difference between Algorithm 1 and the algorithm based on pure random generation of centers is that, for the random generation, Step 1 is removed and Step 3 is replaced by “Compute random centers $\widehat{c}$ inside the room and a random initial radius $\overline{d}$ ”. All the other steps of the algorithm remain the same.

The comparison between the use of random and heuristic starting points is shown in the respective lines in Table 1. We set $\mathrm{ntrials}=100$ and |S| is not allowed to exceed 5. In Table 1, NSolv is the number of solved problems, PSucc is the percentage of the problems for which Gencan has converged to feasible solutions, AvgIMD is the average number of trials necessary to generate the starting point with maximum distance, AvgTMD is the average time per successful trial to find such points, and PBest is the percentage of the problems where each strategy found solutions whose distance is greater or equal than 0.01 (one centimeter). We can see that the heuristic procedure usually generates very good starting points. It is necessary, on average, to run 4 trials to find the best distance during the candidate selection. Also, we observe that most of the starting points result in feasible solutions, while using the random strategy near 65% of the points converge to feasible ones. The heuristic perturbation is able to solve one problem ($7\times 7$ room with $N=30$) more than pure random strategy, while only in 14 problems it finds smaller distances with more than 1cm, the maximum being no greater than 5cm. Finally, we observed that the problems where the random strategy was better are small problems (N up to 30), while the heuristic perturbation performs better on larger ones ($N=50,100$).

Table 1.

Comparison between random generating 100 points in the room and using 100 random perturbations of the solution found by the heuristic procedure

	NSolv	PSucc	AvgIMD	AvgTMD	PBest
Random	86	0.652209	19.232558	0.023853	14
Heuristic	87	0.982299	4.149425	0.006539	12

The previous results encourage us to use the heuristic perturbation to reduce the number of trials. The first obvious improvement would be to use only the heuristic point and eliminate the optimization strategy of Algorithm 1. Using the results from the previous test, we observed that in 50% of the problems, the improvement is smaller than 1cm. However, the best improvement is greater than 37 cm. On average, the improvement is near 3 cm. The computational cost of using Algorithm 1 increases almost linearly as N and ntrial increase. In our tests, the most expensive trial iteration took 0.84 seconds per successful trial, while the most expensive optimization iteration took 0.81 s. Therefore, if only one successful trial is considered, it would increase the response time of the application by at most 2 seconds, in this test, where N up to 100 was considered. We also observed that 75% of the problems needed only 2 trial iterations to find the best trial point. Also, in 56 problems, the best trial point was responsible for the solution of the problem (we recall that |S| best distinct trial points can be stored in Algorithm 1). Hence, we can speed up the execution of the application by drastically reducing the number of trial iterations, if the perturbed heuristic points are used as starting points, without losing too much quality of the solution.

Description of the tool

In this section, we discuss the full implementation details and main functionalities of the tool. First, it is worth noting that although the focus of the tool is on classrooms, it can also be used to distribute tables in restaurants and offices, seats in amphitheaters and airplanes, chairs in waiting rooms, etc. Therefore, in addition to the benefits related to public health, there is the possibility of an economic return by employing a configuration that increases the capacity of physical spaces.

The code of the tool is separated into two projects. The first project implements all techniques of Sects 3 and 4 in Fortran 90, and is available at https://github.com/fsobral/studentpack. The second part concerns the models described in Sect. 2, the whole back-end of the tool and also the website (front-end), and is available at https://github.com/MMagueta/ClassPack. The back-end is implemented in Python using the Flask2 framework. The information of the requests and the implementation of the cache uses the CouchDB3 database and its interface to Python. The website is coded in HTML and uses strongly the Bootstrap and jQuery JavaScript libraries. We have also implemented our own JavaScript library to handle errors, requests, drawings and translations. The communication between front-end and back-end uses the widely accepted JSON format. The tool was designed to be simple and easy to use, but the implementations in each project can be run individually with more complex parameters. For the fixed layout, it is possible to add individual spacing between rows, instead of uniform-distributed ones. For the free layout, there is the possibility to add obstacles, representing doors, windows, columns, cornerstones, furniture, etc.

To run the application, we use the UNIFESP’s computational resources. An Intel 2.4 GHz virtual machine with 4 cores and 4 GB of RAM running Ubuntu 20.04 currently hosts the full application. Therefore, it is possible to process up to 4 problems simultaneously, for which we limit the processing time to 2 min. The idea is to avoid instances with incorrect input data to block the application. For example, seats with dimensions 0.5 mm $\times$ 0.5 mm in a regular-size room may incorrectly result in an instance with hundreds or even thousands of seats. Due to the possibility of several simultaneous accesses to the website, we established a waiting list to solve the requested problems and also set up a database where the solutions are stored. The answer time for already stored solutions is instantaneous and requires no further processing. This is particularly useful in our application, because there are several guidelines from authorities about the number of students and the dimensions of a classroom, which cause the same entries to be not uncommon.

As stated earlier, this work arose from the need to quickly provide a friendly system to assist educational managers in planning the distribution of students within a classroom. The entry point of the tool is shown in Fig. 8. It asks for the “net” dimensions of the room, assuming that the space for the teacher has already been removed. It also asks for the dimensions of the desks, whether it is possible or not to move the desks and the minimum distance between the students. Another important option concerns whether one wants the maximum number of students or the largest possible distance for a fixed number of students, both respecting the minimum expected distance. As already mentioned in Sect. 3, it can be seen in Fig. 8 that one of the constraints that define the room is not physical, since we assume that there is space for the teacher. Therefore, the tool allows the seats to be allocated “over” the right wall of the room. This behavior is observed in Figs. 9 and 10. To avoid such placement, it is necessary to manually reduce the dimension of the desk from the width of the room.

Fig. 8.

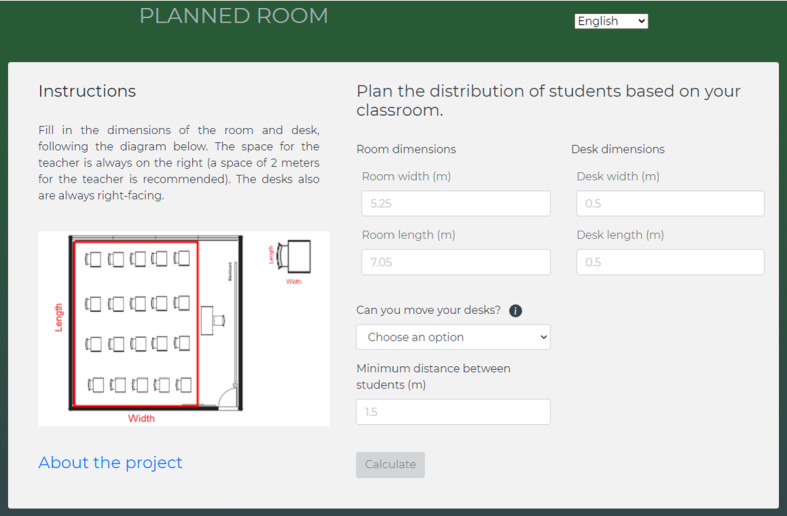
Data input screen in the web application

Fig. 9.

Student distribution result, with the fixed chairs option selected. This example was generated in a $6m\times 8m$ room, with 8 rows of 6 chairs, measuring $0.5m\times 0.5m$ each, maximizing the number of students considering a $1.5m$ distance between them. We can see that, in this case, 12 students can be accommodated, as shown by the white chairs

In rooms such as amphitheaters, the desks are usually fixed on the floor. Another situation in which the fixed layout may be interesting is when there is an interest in maintaining the original layout of the environment. This may happen when, for example, the room is used by multiple groups for short periods of time or when there is no space to store the surplus desks. By choosing the fixed layout option, a map of the positions of the fixed chairs must be created so that the tool can indicate which ones should be occupied, such as in Fig. 9, where the white desks represent the occupied ones. To do this, the number of rows and the number of chairs per row is requested. The tool uniformly distributes the chairs to occupy the entire room. Once the map is generated, we apply the models and solution strategies discussed in Sect. 2. We recall that the tool has the ability to handle non-uniformly distributed rows, but this option was removed from the web application, to keep it simple.

In the free layout option, the tool applies the techniques discussed in Sects. 3 and 4. As a by-product of the process that generates the heuristic initial point, we obtain a feasible configuration for allocating students where they are arranged in rows. This type of solution has the advantage of being fast to obtain and easy to implement, and, therefore, is an extra option of the tool. Obviously, without the restriction of presenting a solution in rows, it is possible to find better results, in terms of distance or number of seats. This can be seen in Fig. 10, where a 5cm increase in the distance was obtained when distribution in rows is not required. Algorithm 1 is run with ntrials set to 100 and $|S|\le 5$. The tool shows the solution and at most other 4 sub-optimal ones, so it is possible to select different layouts. It is also possible to download the position of each desk in a CSV file.

Also considering the option in which the seats can be moved freely, it may happen that the user informs a number of students N and a minimum distance $d_{\mathit{min}}$ for which the problem (3) does not admit a solution. In these cases, the Augmented Lagrangian method often converges to a minimizer of the objective function subject to minimal infeasibility (see (Birgin et al. 2015)). In this situation, the penalty parameter goes to infinity and the algorithm behaves like a pure penalty method. Thus, we believe that the truncated penalty strategy continues to provide a good estimate for the (infeasible) best possible configuration. However, unlike what happens in feasible problems, in various situations the constraint $d\ge d_{\mathit{min}}$, which is not penalized, can not prevent the algorithm from finding configurations where two seats are placed at the same position. For this case, the solution in rows produced by Algorithm 2 is a good infeasible option. In any case, the infeasible solution may still be of interest to the user, so the tool provides it, along with a clear notice that the requested specifications have not been met.

In addition to the web interface, the tool also provides an API, which is the recommended way for planning a large number of rooms. The API is accessed by performing a GET request to a specific address. It can also be used to provide classroom planning for other applications, such as computer programs and smartphone apps. Throughout the API, we were able to perform simulations and provide hundreds of thousands layouts to help the largest national high school exam in Brazil to implement social distancing for more than 130,000 classrooms.

Final remarks

In this paper, we show how Operations Research techniques can contribute to a better allocation of people considering the social distancing protocols inherent to the COVID-19 pandemic. For the case of fixed seats in classrooms we show that integer optimization simple models can be used. For the free positioning case, we use models and non-linear optimization techniques associated with the circle packing problem, that showed good results. In addition, we propose a new heuristic that has also been proved effective not only to provide good layouts by rows, but also to be used as a hot starting point for the optimization problem. The tool is freely available online and, by the end of July 2021, about 500,000 (non-unique) layouts had been generated, which shows a considerable impact on the community.

The problem of fixed seats can be naturally extended to allocation of people in movie theaters or stadiums, for example. For these cases, it would be interesting to consider a not necessarily uniform distribution among all seats. In fact, our program is already prepared to deal with the case in which the distances between the rows are not always the same, although this is not available in the online version. These issues can be easily handled by the model used here, since only the information of the distance between places is used, regardless of the shape of the enclosure and the layout of the seats. However, the user interface would not be so straightforward and a further discussion would be needed to collect the information. In addition, for problems with a very large number of seats, the use of tighter models should be considered. Another very important point to address in the present application is that, within some groups of people, for example, from the same family, social distancing would not be necessary. In this case, perhaps the groups in a certain way can be thought as bigger objects in a binpack problem and a combination with the techniques that we present may be used.

Regarding the situation of free positioning the seats, we highlight the fact that the problem is reasonably well solved with a penalty strategy using a moderate penalty parameter. In fact, it is not difficult to show that, if the Lagrange multipliers for the penalized active constraints are the same, then the penalty parameter does not need to be increased. Therefore, in this situation, the quadratic penalty method becomes an exact penalty method. This fact is valid for general minmax problems and can possibly be better explored. For the case of the application involved in this work, we detected examples where this hypothesis is valid, although it is not always true. It seems reasonable that exploring further the identification of Lagrange multiplier clusters and developing algorithms that use this information could be promising paths.

Another point that deserves attention in future research is to compare the numerical performance of the algorithm when considering different ways of writing non-overlapping constraints. For example, problem (3) would be equivalent if we replace $d^2$ by d in the constraints. In fact, problem’s (3) non-overlapping constraints could be rewritten by applying the square root of both sides of the inequality. Non-differentiation in origin should not be a problem of this formulation, if we consider non-overlapping starting points and impose a positive lower bound for d. In Bueno et al. (2020), it was shown that for linear programming problems, first order estimates for Lagrange multipliers can guarantee an exact solution in a finite number of iterations using an Augmented Lagrangian algorithm. Therefore, since the aforementioned reformulations would reduce the non-linearity of the problem, it may improve the estimate of Lagrange multipliers and consequently the efficiency of the methods.

Just as when dealing with the fixed seats problem, we can also consider rooms with more general formats when it is possible to freely move the seats. If we neglect the size of the desks, we could consider any room format that is described by inequalities. This could be done because we would not have the constraint that the circles must be completely inserted in the container, but only that the center is in the space of interest. To consider the seats dimensions, we would need to know the region where the center should be to ensure a valid position. This could be done, for example in regions defined as the intersection of sets described by polygons and quadratics (Birgin et al. 2013). Other functionalities could also be incorporated, such as allowing the allocation of an individual to a specific fixed place or the assignment of obstacles indicating regions that cannot be occupied. Once again, our tool can deal with these situations but, due to the simplicity required for the application, it is not available online.

Another point that can be better examined is the possibility of adapting the data structure of Birgin and Sobral (2008) within the Augmented Lagrangian function in a way that it does not need to use the formulation given in (6) for taking a single non-overlapping constraint. Still following this line, using the row arrangement given by the heuristic proposed in this work maybe we could eliminate pairs of items that are certainly not touching in the optimal solution. Lastly, we believe that perhaps the incorporation of the dispersion term helps to avoid overlapping constraints and therefore it could be used in some way to solve classic packing problems. In this case, some of the techniques proposed here could be used in the more general context of packing problems.

Finally, it is important to emphasize that the developed tool does not solve other problems inherent to the return of activities, which are equally fundamental variables to guarantee everyone’s safety. Thus, the results pointed out by our work were not intended to be used in isolation, but as a tool to support decision-making, requiring managers to plan accordingly to the general environment context.