Skip to main content
. 2021 Nov 4;118(45):e2105646118. doi: 10.1073/pnas.2105646118

Fig. 2.

Fig. 2.

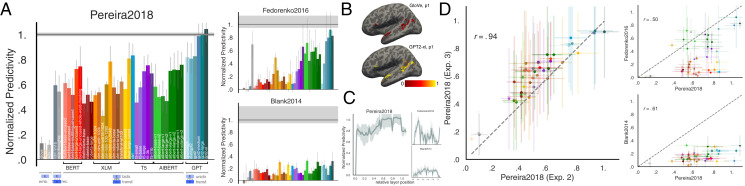
Specific models accurately predict neural responses consistently across datasets. (A) We compared 43 computational models of language processing (ranging from embedding to recurrent and bi- and unidirectional transformer models) in their ability to predict human brain data. The neural datasets include fMRI voxel responses to visually presented (sentence-by-sentence) passages (Pereira2018), ECoG electrode responses to visually presented (word-by-word) sentences (Fedorenko2016), and fMRI ROI responses to auditorily presented ∼5-min-long stories (Blank2014). For each model, we plot the normalized predictivity (“brain score”), i.e., the fraction of ceiling (gray line; Methods, section 7 and SI Appendix, Fig. S1) that the model can predict. Ceiling levels are 0.32 (Pereira2018), 0.17 (Fedorenko2016), and 0.20 (Blank2014). Model classes are grouped by color (Methods, section 5 and SI Appendix, Table S1). Error bars (here and elsewhere) represent median absolute deviation over subject scores. (B) Normalized predictivity of GloVe (a low-performing embedding model) and GPT2-xl (a high-performing transformer model) in the language-responsive voxels in the left hemisphere of a representative participant from Pereira2018 (also SI Appendix, Fig. S3). (C) Brain score per layer in GPT2-xl. Middle-to-late layers generally yield the highest scores for Pereira2018 and Blank2014 whereas earlier layers better predict Fedorenko2016. This difference might be due to predicting individual word representations (within a sentence) in Fedorenko2016, as opposed to whole-sentence representations in Pereira2018. (D) To test how well model brain scores generalize across datasets, we correlated 1) two experiments with different stimuli (and some participant overlap) in Pereira2018 (obtaining a very strong correlation) and 2) Pereira2018 brain scores with the scores for each of Fedorenko2016 and Blank2014 (obtaining lower but still highly significant correlations). Brain scores thus tend to generalize across datasets, although differences between datasets exist which warrant the full suite of datasets.