Table 1.

Supervised machine learning techniques exemplified for binary classification and univariate regression. For ease of interpretation, all examples use a low-dimensional feature space. However, the same principle holds when adding features towards higher-dimensional feature spaces.

Method	Description	Visualization
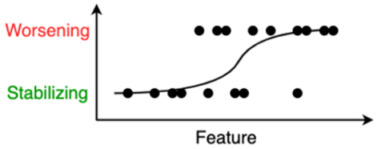
Logistic Regression	Logistic regression identifies the optimal sigmoid curve between the two labels to be predicted, yielding a probability of belonging to either of the two groups. In the illustration: the probability that a person will worsen or stabilize over time.
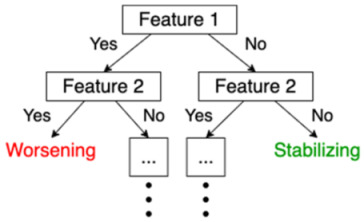
Decision Tree	A decision tree is a sequence of decisions that are made on certain criteria. The last leaves of the tree indicate one of the class labels that are to be predicted.
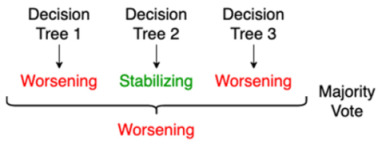
Random Forest	This is an example of “ensemble learning”, meaning that learning, and thus the resulting model, relies on multiple learning strategies, aiming to average the error out [15]. In this case, a random forest consists of multiple decision trees, mitigating the bias introduced by relying on one single decision tree. The ultimate prediction of a random forest classifier is the majority vote of the predictions of the individual decision trees in the random forest.
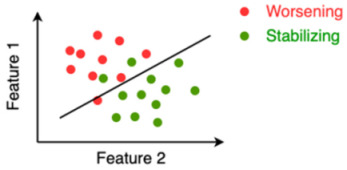
SVM	In case of two features, a support vector machine (SVM) tries to find a line or a curve that separates the two classes of interest. It does so by maximizing the distance between the line and the data-points on both sides of the line, thus maximally separating both classes.
ANN	An artificial neural network (ANN) was inspired by the neural network of the brain and consists of nodes (weights) and edges that connect the nodes. Input data in either raw form or a feature representation enters the ANN on the left (input layer) and gets modified by the ANN in the hidden layers using the nodes’ weights learned during the training phase, so that the input is optimally reshaped, or “mapped”, to the endpoint that needs to be predicted on the right (output layer).
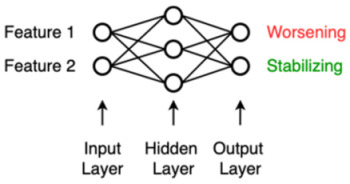
Linear Regression	Linear regression is a technique in which the weight of every input feature is learned, which is multiplied with their respective feature and summed together with the so-called “bias” (also a learned weight but not associated to a feature, i.e., a constant), yielding a prediction that minimizes the error with the ground-truth. In the 2D case, this is the line that minimizes the sum of the squared vertical distances of individual points to the regression line. The learned weights in this case are the slope (β1) and intercept (β0, bias) of the line.
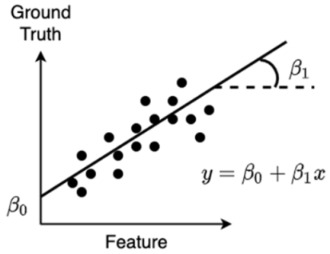