Abstract
In the first phase of axon growth, axons sprout from neuron bodies and are extended by the pull of the migrating growth cones towards their targets. Thereafter, once the target is reached, a lesser known second phase of axon growth ensues as the mechanical forces from the growth of the animal induce extension of the integrated axons in the process of forming tracts and nerves. Although there are several microscopic physics based models of the first phase of axon growth, to date, there are no models of the very different second phase. Here we propose a mathematical model for stretch growth of axon tracts in which the rate of production of proteins required for growth is dependent on the membrane tension. We assume that growth occurs all along the axon, and are able to predict the increase in axon cross-sectional area after they are rapidly stretched and held at a constant length for several hours. We show that there is a length dependent maximum stretching rate that an axon can sustain without disconnection in steady state when the axon length is primarily increased near the cell body. Our results could inform better design of stretch growth protocols to create transplantable axon tracts to repair the nervous system.
Keywords: Stretch growth, Mechano-sensitive channels, Polymerization
1. Introduction
We have previously developed tissue-engineering techniques that exploit a natural “second phase” of axon growth creating long tracts of axons spanning two populations of neurons (Smith et al., 2001; Pfister et al., 2004, 2006) (see Fig. 1). Although generally ignored in the literature, this axon growth mechanism is perhaps the most remarkable of all, allowing axons to extend at seemingly impossible rates without the aid of chemical cues or even growth cones. In the well known “first phase” of axon growth, axons sprout from neurons guided by chemotactic and haptotactic factors and typically extend only up to a few millimeters to reach their targets (Dickson, 2002; Tessier-Lavigne and Goodman, 1996; Wolf et al., 2001; Franze and Guck, 2010). Thereafter, the second phase of purely mechanically stimulated, “stretch growth of integrated axon tracts,” begins as the animal’s body grows. Here, integrated axons spanning body regions that progressively move further apart undergo continuous mechanical tension (Smith, 2009). These forces appear to trigger growth somewhere along the center lengths of the axons, otherwise they would be stretched to the point of disconnection.
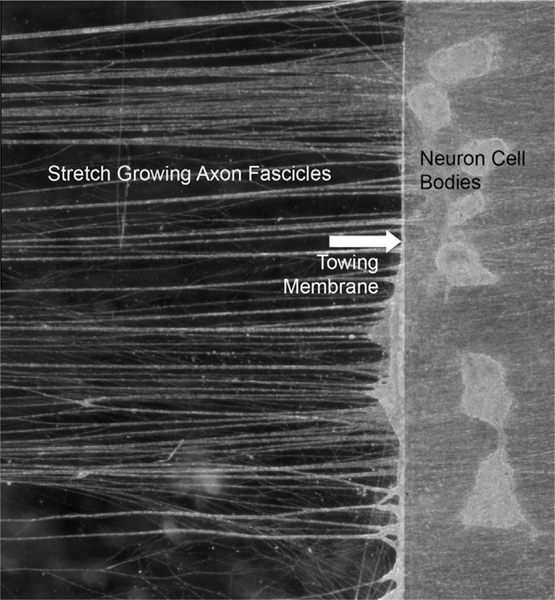
Fig. 1.
Example of the process of stretch growth of integrated axons. Two populations of neurons are plated on two adjacent substrates, one of which serves as a towing membrane (swine dorsal root ganglia neurons shown on towing membrane, arrow). Over a few days, axons sprout and connect the two neuron populations. A microstepper motor system then pulls the towing membrane away from the adjacent substrate at accelerating rates. This induces tensile forces on the spanning axons, which respond by growing in length to mitigate the stress. This process also causes axons to coalesce and become organized into relatively straight large fascicles spanning the two neuron populations (fascicles extending to and from towing membrane shown on left). This extreme axon growth mechanism can produce fascicles of at least 10 cm in culture, and many meters in animals. Shown is approximately 0.5 cm of axon fascicles that were grown to 5 cm in total length.
While relatively unknown, this important form of axon growth occurs in white matter tracts and nerves, and represents a unique form of tissue expansion that does not involve cell division. For example, our calculations of the growth of blue whale spinal cord during development show that axons can increase an astonishing 3 cm in length per day (Smith, 2009), presumably to match the growth of the vertebrae. This increase in volume in the axon is likely more than doubling the volume of the entire neuron cell body each day as well, rivaling the growth capacity of the most aggressive cancer cells (Smith, 2009). The exceptionally elongated geometry of axons must pose a huge challenge for transport of cellular building materials, especially at the extremes, such as in the 30 m long spinal axons of blue whales (Smith, 2009).
We demonstrated this natural extreme growth mechanism in the laboratory using bioreactors that can progressively separate two integrated populations of neurons in culture at accelerating rates (Smith et al., 2001; Pfister et al., 2004). Opposing current dogma of the limitations of axon growth, this process has produced tracts containing over 1 million axons grown up to 10 cm long at rates of up to 1 cm per day (Pfister et al., 2004, 2006). Yet, despite this rapid stretching, we have found that the axon tracts maintained a normal lengthwise morphological appearance and that their internal ultra-structure was completely normal. In particular, a normal complement of microtubules and neurofilaments was found per cross section area for rapidly stretch grown axons. Surprisingly, however, the average diameter of these axons had even increased compared to non-stretched axons (Pfister et al., 2004, 2006).
To explore the cellular dynamics and boundaries of axon extension during the first phase of axon growth, several groups have developed computational models, with a focus on polymerization of microtubules as axon cytoskeleton building blocks. In most of these models, as the growth cone is guided forward, tensile forces are induced at the axon terminal or tip, just behind the growth cone (Heidemann and Buxbaum, 1994; Heidemann et al., 1990, 1995). In turn, it is assumed that these forces trigger building of the microtubule selectively in this region (Van Veen and Van Pelt, 1994; Samuels et al., 1996; Nguyen et al., 2013). However, once the target is reached typically not more than a few millimeters away, integration and synapse formation essentially abolish the growth cone. Also, recent work has shown that growth occurs over the entire length of a towed axon causing an increase in axon diameter when stretching at high rates causes a reduction in the axon cross-sectional area (Lamoureux et al., 2010; Holland et al., 2015). Therefore, current mathematical models do not appear to account for mechanical influences during the extreme second phase of axon growth and expansion of tracts over tens of centimeters for humans and even many meters for very large animals. Furthermore a model of O’Toole et al. (2008) suggests that growth is dependent on tension through viscosity and adhesions. However, the specific role of stretch activated ion channels in axon stretch growth has not been explored (Franze and Guck, 2010; Sigurdson and Morris, 1989; Franze et al., 2009). Here, we propose a model for stretch growth of integrated axon tracts based on overall mechanical stimulation resulting in very regional microtubule polymerization (in steady state) and relative contribution of stretch activated channels in the process.
2. A new model for stretch growth of integrated axon tracts
We assume that the polymerization reaction (of microtubules) in stretch growth occurs at the base of the axon near its junction with the cell body, to change the axon length L(t) (see Fig. 2(a)), and possibly also along the axon, to change the cross-sectional area A(t) (Lamoureux et al., 2010). Hence, the total mass M(t) of the polymerized species (microtubules) is proportional to AL. If the concentration of the monomer species is m(t) (assumed uniform over the volume of a reaction chamber) then one can write kinetic equations for and as described in Michael et al. (2016), for example. However, this does not suffice for us since we wish to know the evolution of both L(t) and A(t) separately, while an equation for is proportional to the sum . Furthermore, the monomer concentration is not uniform everywhere due to active transport of building materials, and the reactions that increase L(t) are assumed to be localized at the axon hillock (Lamoureux et al., 2010), so we write separate equations for and . To account for polymerization at the base of the axon we note that if the concentration of monomers in the soma is Qs then d
| (1) |
where t is time, and , where e is the length of one monomer, kon is an on-rate and koff is an off-rate. is the number of connected monomers making up a linear polymer and . Eq. (1) for the kinetics of polymerization is applicable to linear polymers, including microtubules and F-actin, as summarized in Howard (2001). It has been used in models for growth of neurites since at least the 1980s as described in Van Veen and Van Pelt (1994). Samuels et al. (1996) use a similar equation for capturing the rate of change of length, but they drop the off-rate β1 and assume that polymerization occurs at the tip of the axon near the growth cone which advances to extend the axon while the cell body, or soma, is stationary. In the experiments of Pfister et al. (2004, 2006) the growth cone is abolished and the tip of the axon is stationary after two sets of neurons growing toward each other have formed a junction. One set of neuronal cell bodies is then pulled away, so that increase in length L(t) of the microtubules likely occurs at the axon hillock. Evidence for polymerization at (and near) the axon hillock can be found in the “reverse towing” experiments described in Lamoureux et al. (2010). This is why Qs enters Eq. (1) for the kinetics. Now, for the rate of growth to be positive we must have (Boal, 2002). Let us assume that the monomers are produced in the soma at a rate I (in units of number of monomers per second). These monomers are being consumed by the polymerization reaction given by Eq. (1), transport of monomers away from the soma by active and passive processes and by spontaneous diffusion into the axon. We are assuming here that the polymerized microtubules do not diffuse and are not transported, consistent with the assumptions of Van Veen and Van Pelt (1994) and Samuels et al. (1996). If we assume that the concentration of monomers at the tip of the axon is Qt, then the diffusive flux of monomers away from the soma can be written as , where D is a diffusion constant and we have approximated the concentration gradient of the monomers as being constant (Van Veen and Van Pelt, 1994; Samuels et al., 1996). So, the rate of change of monomer concentration in the soma is given by:
| (2) |
where A is the axon cross-sectional area which possibly depends on time, Vs is a small volume in the soma where the polymerization reaction occurs, a is the cross-sectional area occupied by a single micro-tubule, M is a growth independent transport coefficient and F is a growth dependent transport coefficient. Once again, the production and diffusion terms on the RHS are the same as in Van Veen and Van Pelt (1994) and Samuels et al. (1996) and the transport terms are the same as in Samuels et al. (1996). But, the sign of the term multiplying F in the above equation is different from that in Samuels et al. (1996) because in stretch growth the tip of the axon is stationary with the soma being pulled away, while in the situation analyzed by Samuels et al. (1996) the soma is stationary and the tip moves away due to the advancing growth cone. is the number of microtubules in a cross-section of area A, so is the rate of disappearance of the number of monomers at the axon hillock (near the soma) due to the polymerization reaction. To convert this to a rate of change of monomer concentration we divide by the small volume Vs and this gives the third term on the RHS. This term is not present in the equation for in Van Veen and Van Pelt (1994) and Samuels et al. (1996) because polymerization is assumed to occur at the axon tip in these papers, not at the axon hillock.
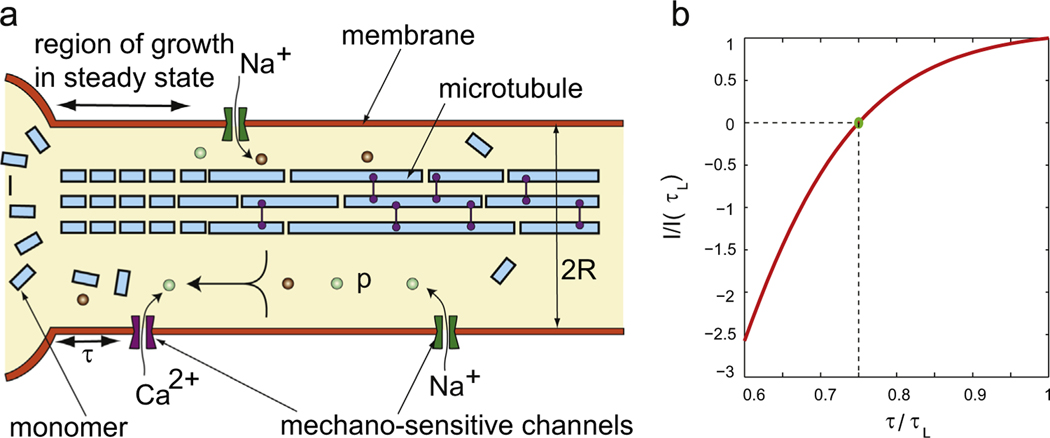
Fig. 2.
A schematic of a neuron undergoing stretch growth. The polymerization occurs at the junction of the axon and soma as well as all along the axon. The production of monomers in the soma depends on the probability of mechanosensitive channels in the membrane being open. This probability depends on the membrane tension, which, in turn, depends on how fast the neuron is being stretched. Thus membrane tension indirectly determines how fast a neuron can grow.
When the axon is stretched up to twice or thrice its original length in a few hours, initially its area of cross-section becomes smaller because growth cannot keep up. But, after 10–20 h the axon recovers its original cross-sectional area (Holland et al., 2015; Lamoureux et al., 2010). Neither Van Veen and Van Pelt (1994) nor Samuels et al. (1996) accounted for the change in axon cross-sectional area, but Samuels et al. (1996) did account for active transport of building materials which are required for assembly away from the soma through growth dependent and independent active transport terms. We assume that A is proportional to the number of microtubules in the cross-section. Hence, rate of change of A is given by
| (3) |
where γ and are constants. The first term on the RHS quantifies creation of new microtubules from monomers and the second term quantifies disappearance of existing microtubules in the cross-section. The second term on the RHS should be proportional to the local number of microtubules, but since we assume that the cross-sectional area is proportional to the number of microtubules we insert A into the second term. Qt enters the kinetic equation above because it represents monomer concentration away from the soma which is increased by active and passive transport towards the tip due to which the increase in area A occurs.
In the models of Van Veen and Van Pelt (1994) and Samuels et al. (1996) the concentration of monomers away from the soma was Qt and its rate of change was affected by polymerization at the tip which caused an increase in L(t). In the stretch growth experiments modeled here the increase in L(t) happens due to polymerization at the axon hillock and affects the concentration of monomers Qs(t). In the stretch growth experiments of Pfister et al. (2004, 2006) the tip is stationary, so we will assume that the rate of change of Qt(t) is affected by the change in A(t), not L(t), as quantified by the second term on the RHS of Eq. (4). Hence, the equation for the concentration of monomers at the tip of the axon is:
| (4) |
where Vt is a small volume at the tip of the axon. Monomers arrive at the tip by diffusion and transport and could be consumed there if polymerization/depolymerization of microtubules occurs causing a change in cross-sectional area A(t). Since A is assumed constant in Van Veen and Van Pelt (1994) and Samuels et al. (1996) the second term in the RHS above does not appear in their equations. Also note that the transport term which is proportional to the local pulling speed does not appear in the equation for because the tip is stationary. This is in accordance with a linear (in a coordinate x along the axon) stretch flux given in O’Toole and Miller (2011). Also, as in O’Toole and Miller (2011) and Lamoureux et al. (2010) we assume that the area A is the same for the entire length of the axon.
Finally, we make a few more remarks to contrast our model against those of Van Veen and Van Pelt (1994) and Samuels et al. (1996). We will assume where A0 is the equilibrium cross-sectional area of the axon (for example, the cross-sectional area before stretching begins), so that there is a net flux of building materials toward the tip of the axon only if axon cross-sectional area becomes smaller and needs to be restored to its equilibrium value. By choosing this form for M we get M = 0 when A = A0 which is consistent with the assumptions (M = 0, A = A0, fixed) of Samuels et al. (1996). If we identify with G in Samuels et al. (1996) then a constant G in Samuels et al. (1996) is again consistent with a constant A = A0. If we hold A(t) constant for all t then our equations reduce to those of Samuels et al. (1996) with only one modification pertaining to the location where the increase in length occurs (axon hillock in this work, axon tip in Van Veen and Van Pelt, 1994; Samuels et al., 1996). In Table 1 we list our variables and the corresponding variable names in the model of Samuels et al. (1996) with N=1. Following Samuels et al. (1996) we can write our equations for stretch growth in non-dimensional form and identify the few dimensionless groups that control the process. This exercise is done in Section 4 for the special case when A = A0.
Table 1.
Our list of variable names compared to Samuels et al. (1996).
| This work | Qs | Qt | D | A | L | α | β | I | A/ae | F | M | Vs | Vt |
| Samuels et al.(1996) | C 0 | C 1 | D | A | L 1 | α | - | S | G | F | I 1 | Vsoma | Vtip |
2.1. Steady-state solution
It is possible that I depends on external factors. For example, increasing tension will cause mechanosensitive channels in the membrane to open causing an influx/outflux of Na+, K+, Ca2+ and other ions. These could carry a signal to the soma either directly in the form of calcium waves or through active transport by motors to cause a change in I. We will admit this possibility into our analysis later and treat I as a constant for now. The differential equations above need to be solved numerically. But, since in stretch growth L(t) is linear in time (with a constant pulling rate C1 specified) we will try to get a simple solution by plugging in the following ansatz into the differential equation:
| (5) |
If we assume that the axon is long enough so that diffusion can be neglected we find that all equations are satisfied if
| (6) |
Thus, for given pulling rate C1, I, A = A0, Qs and Qt are all constants at steady state. Neglecting diffusion is justified because the solution to the non-dimensional equations with constant A = A0 hardly changes in response to a change in D over a few orders of magnitude (see sensitivity analysis in appendix). This means that the concentration gradient produced by the above solution is so small that diffusion plays a very minor role in stretch growth. The last expression above can be rearranged by solving the quadratic equation for C1 in terms of I and other quantities. Thus, if I is given then C1 in steady-state depends on the growth dependent flux term proportional to F which has been shown to make a major contribution to transport of materials in the axon in O’Toole and Miller (2011) as we confirm in the sensitivity analysis performed in the appendix. If F=0 then the production rate I and the pulling velocity C1 are linearly related in steady state. In particular, if in steady state C1 = 0, I must also be zero. For such an axon we expect , since otherwise there will be diffusion which violate equilibrium. Hence, we require
| (7) |
For given α, β, γ and this is an equation that sets the value of A0. There are several other points to be noted about this steady state solution. First, if C1 > 40 then , as required for polymerization driven growth. If (which happens when C1 < 0) then depolymerization will happen and the axon will shorten. Second, there is a concentration gradient of building materials along a long axon in steady state stretch growth with concentration being higher at the soma. Hence, diffusion plays a role in transport, albeit small. On the other hand, net active transport due to molecular motors is zero in steady state, since . In other words, in steady state there is very regional microtubule polymerization near the cell body. Third, if C1>0 the concentration of building materials all along the axon is higher than the critical value required for polymerization and growth to occur all along the axon. This ensures that if the axon is damaged somewhere along the length then it can be repaired.
2.2. Application to experiments quantifying evolution of axon cross-sectional area
Now consider the stretch and hold experiments of Holland et al. (2015) and Lamoureux et al. (2010) in which the axons are stretched for 1–5 h and then held at constant length for up to 20 h. We will focus on experiments in which axons are stretched up to 1.6 (or less) times their original length. The area A decreases initially so that the total volume of the axon remains fixed. Let us set t=0 when stretching is stopped and call . As time progresses, the axons are held at constant length and the cross-sectional area comes back to A0 over several hours. Recall that when C1 = 0, the steady state (or equilibrium) value of A is A0. We now want to determine how A(t) evolves to equilibrium using our differential equations above. Since , . Since the axon has only been stretched to 1.6 times its original length we assume that diffusion quickly causes Qt to become equal to Qs, so that . Note that a protein of radius 3 nm has a diffusion constant μm2/s in water at room temperature. Thus, it takes of 1 monomer about 1 min to diffuse a distance of 100 μm (see Howard, 2001). This is negligible in comparison to the few hours it takes the axon cross-sectional area to reach its equilibrium value; hence, our assumption that Qt quickly reaches is justified. Then, from the last three differential equations we get
| (8) |
| (9) |
| (10) |
The first and second equations together imply that all the monomers actively transported from the soma assemble to increase the area A of the axon. Solving the second equation for A gives
| (11) |
where we can determine p from the initial condition at t = 0. Hence, the solution for A is
| (12) |
Solving the first equation and using the initial condition for A gives
| (13) |
The constant in the exponential must be the same in the two different expressions for A(t). Thus,
| (14) |
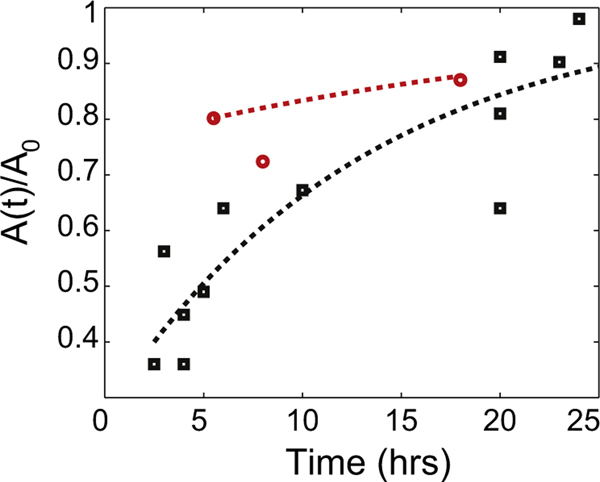
This means that , or active transport of building materials is linked with the growth in axon cross-sectional area. Now, the third equation says that the production rate I must depend on t as during recovery to the equilibrium cross-sectional area. We can estimate from the stretch and hold experiments of Holland et al. (2015) and the “reverse towing” experiments of Lamoureux et al. (2010). Data from five stretch and hold experiments extending to more than 20 h in Fig. 3 of Holland et al. (2015) and from neuron 1 in Table 2 of Lamoureux et al. (2010) appear in Fig. 3. In the same figure we plot two curves using Eq. (12) – the red dashed line capturing the trend in Lamoureux et al. (2010) has h, and the black dashed line roughly capturing the trends in Holland et al. (2015) has h. In reality, each neuron in Fig. 3 of Holland et al. (2015) has a different , so 13 h is an estimate of the average for these neurons. Fig. 3 shows that Eq. (12) is a good first approximation to the recovery of axon caliber seen in stretch and hold experiments. We know from Howard (2001) that moles/m3. We take a = A0/100, meaning there are about 100 microtubules in an axon cross-section (Yu and Baas, 1994). So, from (14) we find that m ≈ 10/A0 in SI units (the units of m are m/s, same as velocity).
Fig. 3.
Experimental data on recovery of axon cross-sectional area from Lamoureux et al. (2010) (red circles) and Holland et al. (2015) (black squares) compared with Eq. (12) from our model. h for the black dashed line and h for the red dashed line. (For interpretation of the references to color in this figure caption, the reader is referred to the web version of this paper.)
2.3. Application to stretch-growth experiments
Now, let us determine how steady state is reached when an axon is pulled at a constant speed C1. We will assume diffusion to be negligible again, but we will not assume because the soma is moving away from the tip so that transport toward the tip will be hindered due to a stretch flux in the opposite direction. Then, from (1) . We differentiate (3) once with respect to time t and plug in from (2) for to get a differential equation for A(t) alone:
| (15) |
Call y = A − A0, then the above equation is
| (16) |
and its solution is
| (17) |
where C5 and C6 are constants and λ1 and λ2 are given by
| (18) |
| (19) |
Note that when C1 = 0, and . Recalling that , in SI units, and it is easy to see that the term will die out in a very short time. Thus
| (20) |
where λ1 depends on the stretching speed C1 through (18). Also, if and then we can express λ1 as
| (21) |
If we apply the initial condition that then we can find C5, so that
| (22) |
As , and . Since A(t) is known, Qt(t) can be computed from (2) and I(t) can be computed using (4) as follows:
| (23) |
The first two terms represent the steady state value of I and the last term proportional to shows how I(t) reaches its steady state for given C1.
3. Membrane tension dependent production rate
Although our analysis above shows how the axon cross-sectional area A changes during stretch growth, it puts no limit on the velocity C1 at which the axons can be pulled for growth to keep up. The resolution of this difficulty lies in determining how the rate of monomer production I depends on the tension τ in the axonal membrane. We show in the appendix that tension τ in the membrane will be isotropic for long cylindrical axons if rate effects can be neglected. The equilibrium equation for the cylindrical membrane of an axon of radius R shows that the isotropic tension τ is related to the hydrostatic pressure difference p between the inside and outside of the axon through (see the appendix):
| (24) |
The cell must, of course, ensure that the tension τ remains below the failure tension τL of the axonal membrane. A stretched neuron might do this on short time scales by releasing the reservoirs of invaginated plasma membrane (caveolae), thereby decreasing the membrane tension and axon radius as observed by Holland et al. (2015) (see also Dennerll et al. (1988) and Siechen et al. (2009). Alternatively, the volume and membrane could be redistributed during stretch, resulting in longer, but thinner axons. In fact, the membrane of the axon is a viscoelastic material which when stretched along the length will contract along the circumferential direction at short times if no growth takes place (see the appendix). However, if stretching continues over long times then the cell must produce materials to the build the axon, otherwise τ will increase beyond the failure tension and the cell will rupture. As such, the cell must “sense” the increasing membrane tension and increase the rate of production I so that growth keeps up with the stretching. Furthermore, our previous in vitro studies demonstrated that the cells appeared to be conditioned to anticipate that accelerating stretch rates would continue, thereby accelerating the production of building materials (Pfister et al., 2004).
A potential source of this cell signaling during stretch growth is likely mechanosensitive channels in cell membranes that have been shown to open in other circumstances when the tension increases (Sigurdson and Morris, 1989; Franze et al., 2009; Nelson, 2004). Of course, signaling of the mechanical state of the axon to the soma could also occur due to cytoskeletal remodeling which happens in many types of cells in response to stretch (Tojkander et al., 2012). Thus, the proposed signaling mechanism based on ion channels is one of many possibilities. Opening of these channels can cause an influx of ions such as Na+ and Ca2+. While Na+ influx can initiate an action potential for fast signaling, increases in intracellular Ca2+ concentration can play an important role in phosphorylation of proteins and activation of transcription factors, which in turn can influence production of tubulin monomers in the soma. Calcium waves could also carry a message to the soma (Rishal and Fainzilber, 2014) that can lead to increased I. While the exact mechanism may not be known it is reasonable to assume that I depends linearly on the probability popen of the mechanosensitive channels being open. The quantitative dependence of this probability on the membrane tension has been documented in the literature (Wiggins and Phillips, 2005; Haselwandter and Phillips, 2013). Using those expressions we assume that the monomer production rate I is a monotonic function of the tension τ. We will assume that I is linearly related to the probability popen of channels being open. For simplicity, we will take this probability as (Haselwandter and Phillips, 2013)
| (25) |
Here, C3 and C4 are constants, is the free energy difference between the closed and open states of the channel and is the difference in cross-sectional area between the open and closed states. ΔG is usually on the order of several kBT while ΔA is several tens of nm2. Note that increases when the tension τ increases but it saturates at 1. We could determine C4 in terms of the other constants by insisting that I = 0 when the tension τ = τ0 the rest tension of the axon membrane. If we do so then
| (26) |
Going back to our equations we notice that in steady state we must have , so that
| (27) |
This equation relates the pulling velocity to the tension in the axonal membrane in steady state. As C1 increases τ also increases. This result has some implications; (27) sets a limit on the maximum C1 at which polymerization can keep up with the pulling. This maximum is reached when which happens as , and is given by . is not realistic because if the tension τ reaches the failure tension τ = τL then the membrane will rupture. The C1 at which the failure tension τ = τL is reached is
| (28) |
We will try to make some estimates using this model. For simplicity, let us take
| (29) |
Of these, ΔG and ΔA values have been obtained from Haselwandter and Phillips (2013), Haswell et al. (2011), and Phillips et al. (2009). As for the failure tension, Dai et al. (1998) report it to be 10−2 N/m for molluscan neurons. However, Hategan et al. (2003) point out that high tensions around 10−2 N/m cause lysis within a very short time (on the order of seconds), where as tensions on the order of 10−3 N/m or lower can be sustained by cells before lysis for more than an hour. Since axons are stretched for several days without lysis we take τL = 10−3 N/m. Hategan et al. (2003) report that for spread red cells on substrates (coated with poly-L-lysine) the static tension is 0.8 mN/m. Since the axons described in Pfister et al. (2004, 2006) were cultured on poly-L-lysine and collagen coated Aclar film we expect that their membranes will have a static tension similar to the red cells described in Hategan et al. (2003), so we take τ0 = 0.75τL. According to Smith (2009) (or about 30 nm/s). Hence, we get m/s (in SI units). Finally, an explicit expression for I is
| (30) |
In the previous section we showed how I(t) evolves to reach steady-state for given pulling speed C1. In this section we have obtained an expression for the dependence of I on the membrane tension τ. Thus, we can now determine how τ(t) evolves to a steady state tension for given C1 by equating (30) to (23) (see Fig. 4 in which cross-sectional area and tension are plotted as functions of time). If we further assume that the tension τ in the membrane is related to the hydrostatic pressure difference p across the cylindrical axon through
| (31) |
then we find that p depends only on the pulling rate C1 because both τ and A depend only on the pulling rate C1. We do not compute an analytical form for the dependence of p on C1 here, but recall that a recent study (Fernandez and Pullarkat, 2011) combining osmotic shock experiments with theory concluded that a non-zero hydrostatic pressure difference between the outside and inside of a PC-12 cell is required to quantitatively capture its response to osmotic shock. They claimed that due to the viscoelastic nature of the cell cytoplasm this hydrostatic pressure difference should depend on the volumetric strain rate in a non-linear way. Rather interestingly, they say that this non-linear viscoelastic response has its origins in the microtubulues in the neurite. Our argument for the non-linear dependence of τ (and hence, p) on the pulling rate C1 is also connected to the presence of micro-tubules and other structural components in the axon cross-section.
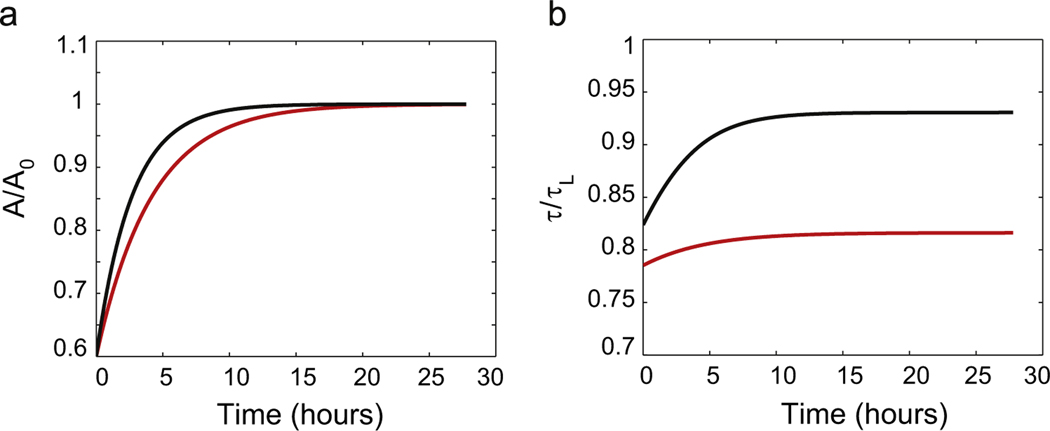
Fig. 4.
(a) Axon cross-sectional area as a function of time. We start with the initial condition A = 0.6A0 and apply two different stretching speeds (red curve) and (black curve) where . A(t) reaches the asymptotic value A0 in several hours in both cases. (b) Membrane tension as a function of time. For long times the membrane tension also tends to a constant that depends on the pulling speed. The higher the pulling speed, the higher the steady state tension. If the pulling speed is larger than the membrane tension exceeds the failure tension τL causing disconnection of the axon. (For interpretation of the references to color in this figure caption, the reader is referred to the web version of this paper.)
4. Limits on stretch-growth
Suppose during initial stretching the failure tension τL is reached due to purely mechanical stretching of the membranes. As a result the cell ramps up protein production I to its maximum. Growth starts, new membrane is added causing the tension to go down for any . Eventually, the cell settles into a steady state with τ < τL. The limit on L(t) is set by the requirement that τ remains at τL. If this is the case then I and A = A0 also remain constant (a constant A for growth over several days was reported in Lamoureux et al., 2010). We will find the limiting L(t) by integrating three ODEs with the assumption that τ = τL, so that I is at its maximum. For this it is convenient to use the non-dimensionalization that Samuels et al. (1996) applied. They chose the scales:
| (32) |
which lets us define non-dimensional quantities:
| (33) |
Now the non-dimensional ODEs for stretch growth are:
| (34) |
| (35) |
| (36) |
where we have neglected the contribution of koff (because it is expected to be small) and the constants , and are:
| (37) |
We integrated this system of ODEs in MATLAB. We used = 5.7 and = 5.2 following Wissner-Gross et al. (2011) and set = 0 for simplicity. The resulting curve for vs. looks very similar to the L(t) curve in the paper by Smith (2009) (see Fig. 5). This suggests that when τ = τL the time scale day and the length scale mm. For normal growth (not stretch growth) Wissner-Gross et al. (2011) give h and μm. Hence, it must be that α (or equivalently kon) for stretch growth is about 4 times smaller than that for normal growth, and I for stretch growth is about 3–5 times bigger than that for normal growth.
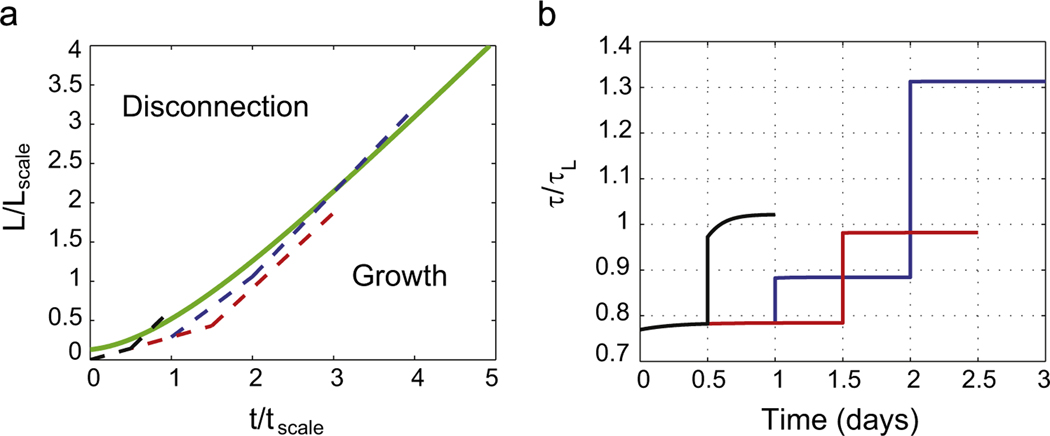
Fig. 5.
(a) The green line shows the limiting L(t) curve for = 5.7, = 5.2 and l(0) = 0.13. The blue dashed line has the following trajectory for day 1 for day 2 and for days 3 and 4. The red dashed line has the following trajectory for day 1 and 12 h on day 2, , thereafter. The black dashed line has the following trajectory for 12 h, thereafter. The evolution of the tension τ is plotted on the right. (b) The tension crosses τL for the blue and black curves, but not for the red curve. Therefore, the blue and black protocols lead to disconnection, but the red protocol does not. Note also that in the black protocol we could exceed for several hours without causing disconnection because it takes time for the tension to reach the failure value. We have mimicked the experiments shown in Fig. 4A of Smith (2009).
This approach also reveals that crossing the limiting L(t) curve from below using piecewise linear trajectories causes the tension to exceed τL and will result in disconnection. This is demonstrated for two different piecewise linear trajectories in Fig. 5(a) shown as blue and black dashed lines. For each of these trajectories we plot the tension in Fig. 5(b) as blue and black lines, respectively, with initial tension about 0.78τL. The tension eventually exceeds the value for lysis for both these trajectories. A piecewise linear trajectory that does not cross the limiting curve is also shown as the red dashed line in Fig. 5(a). For this trajectory the tension remains below the failure value. Similar trajectories can also be found in Fig. 4A of Smith (2009).
5. Discussion
We present the first analytical model to identify mechanisms that govern extreme stretch growth of integrated axon tracts during development and experimentally in vitro. Our findings differ greatly from those shown for first phase of axon growth, where polymerization of microtubules occurs at the tip of the axon (Heidemann and Buxbaum, 1994; Heidemann et al., 1990, 1995). Indeed, we find that once the axon reaches and integrates with its target, the second phase of very rapid axonal growth occurs at the opposite end of the axon, along the junction of the axon hillock and the soma. This is preceded by a short phase in which growth occurs all along the axon so that its cross-sectional area is restored to its equilibrium value after an initial reduction due to rapid stretching, consistent with the observations of Lamoureux et al. (2010).
The model also describes the dependence of microtubule monomer production rate in the soma on the tension in the axonal membrane. This allows us to quantitatively explain observations of axon stretch growth in vitro, such as apparent cellular conditioning to anticipate accelerating rates of growth by accelerating production of building materials. For the model, the conditioning that drives the rate of monomer production depends linearly on the probability of mechanosensitive channels being open. This probability has been shown to depend on the mechanical tension in the membrane in a quantitative way that accounts for the free energy differences between the open and closed states of the channel (Haselwandter and Phillips, 2013). By connecting this probability in a precise way to the rate of protein production in the soma we have given a mechanism for how tension can regulate the response of a growing cell. There have been other models in the literature that have quantitatively accounted for the tension dependence of growth (Franze et al., 2009), but they are phenomenological. In contrast, our model arrives at this dependence from the microscopic physics of the gating of ion-channels and the polymerization of microtubules. It is, however, important to remember that the model for signaling proposed above is one of many possibilities.
Moreover, the model partially accounts for the challenge of axonal growth exceeding the capacity of axonal transport. In the first phase of axon growth during development or regeneration shown in vivo and in vitro, there appears to be a consistent growth rate limitation of approximately 1 mm/day (Smith, 2009), which matches the slow axonal transport rate determined for a key cytoskeletal protein, neurofilament protein (Brown, 2003; Nixon, 1998; Brown, 2000). However, for the second phase of axon tract stretch growth, this slow transport rate can clearly be outpaced in large animals. At the extreme growth rate of the blue whale, even established limits of fast axonal transport at about 3 cm/day (Grafstein and Forman, 1980) for cargoes such as microtubule proteins would struggle to keep pace with stretch growing axons (Smith et al., 2001; Smith, 2009). An evolutionary solution to accommodate limitations of axonal transport during extreme stretch growth may be by extruding new axon structure directly from the cell body. In this scenario, the growth velocity reflects the sum of axonal transport plus extrusion, thereby exceeding conventional rates of transport. This mechanism of axon extrusion also mitigates the necessity of transporting all components needed for complete construction of up to centimeters of axon length per day very distant from the cell body.
Although we have previously demonstrated the boundaries of accelerating extreme axon stretch growth in vitro (Pfister et al., 2004), factors leading to growth verses rupture were not identified. The results of our mathematical model demonstrate that the neuron reaches a steady state growth rate after an initial transient. In this steady state the tension remains constant as the axon grows at a constant speed. We posit that the tension must remain below the rupture tension of the membrane at all times. If the growth program is designed in such a way as the membrane is exactly at rupture tension at all times then the neuron is pushed to its limits – stretching any faster than the rate dictated by this limiting growth program which results in disconnection.
While we have provided a microscopic physical model for stretch growth of neurons significant challenges still remain in our understanding of the process. For example, we do not have a quantitative model for how opening of ion channels sends the signal for the cell to change its rate of production of proteins. Such a model will allow us to quantify how other types of stimuli (e.g. chemical and electrical) could also influence stretch growth. It could also be that other signaling mechanisms, such as cytoskeletal remodeling, could cause the cell to change its rate of protein production and should certainly be explored. Again, tension in the axon surely depends on the nature of the neuron’s attachment to its substrate. We have not accounted for this in our model, but we anticipate that this can be accomplished by following the ideas of O’Toole et al. (2008). Such an extension of our model could explain how substrate mechanical properties influence stretch growth (Franze and Guck, 2010).
Overall, these findings may contribute to the general understanding of the nervous system morphogenesis during development by providing potential mechanisms that underlie very rapid growth of axon tracts and nerves. In addition, the new model provides considerations of the mechanical limitations and potential of stretch growth of axon tracts that can be used to refine input parameters for nervous tissue engineering. Indeed, as engineered nervous tissue constructs have shown promise for repairing nervous system damage in experimental models, optimized growth methods to create long transplantable axon tracts may accelerate the path to clinical application (Pfister et al., 2006, Iwata et al., 2006; Huang et al., 2008, 2009).
Supplementary Material
Acknowledgments
We thank Ms. Rashmi Pujari for help with some of the figures. P.K.P. acknowledges partial support through a grant from the University Research Foundation at the University of Pennsylvania.
Footnotes
Conflict of interest statement
None declared.
Appendix A. Supplementary data
Supplementary data associated with this article can be found in the online version at http://dx.doi.org/10.1016/j.jbiomech.2016.11.045.
References
- Boal D, 2002. Mechanics of the Cell. Cambridge University Press, Cambridge, UK. [Google Scholar]
- Brown A, 2000. Slow axonal transport: stop and go traffic in the axon. Nat. Rev. Mol. Cell Biol 1 (2), 153–156. [DOI] [PubMed] [Google Scholar]
- Brown A, 2003. Axonal transport of membranous and nonmembranous cargoes: a unified perspective. J. Cell Biol 160 (6), 817–821. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dai J, Sheetz MP, Wan X, Morris CE, 1998. Membrane tension in swelling and shrinking molluscan neurons. J. Neurosci 18 (17), 6681–6692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dennerll TJ, Joshi HC, Steel VL, Buxbaum RE, Heidemann SR, 1988. Tension and compression in the cytoskeleton of PC-12 neurites. II: Quantitative measurements. J. Cell Biol 107(2), 665–674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dickson BJ, 2002. Molecular mechanisms of axon guidance. Science 298 (5600), 1959–1964. [DOI] [PubMed] [Google Scholar]
- Fernandez P, Pullarkat PA, 2011. The role of the cytoskeleton in volume regulation and beading transitions in PC12 neurites. Biophys. J 99, 3751–3759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franze K, Gerdelmann J, Weick M, Betz T, Pawlizak S, Lakadamyali M, Bayer J, Rillich K, Gogler M, Lu YB, Reichenbach A, Janmey P, Kas J, 2009. Neurite branch retraction is caused by a threshold-dependent mechanical impact. Biophys. J 97 (7), 1883–1890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franze K, Guck J, 2010. The biophysics of neuronal growth. Rep. Prog. Phys 73, 9. 10.1088/0034-4885/73/9/094601 (Art no. 094601). [DOI] [Google Scholar]
- Grafstein B, Forman DS, 1980. Intracellular transport in neurons. Physiol. Rev 60 (4), 1167–1283. [DOI] [PubMed] [Google Scholar]
- Haselwandter CA, Phillips R, 2013. Connection between oligomeric state and gating characteristics of mechanosensitive ion channels. PLoS Comput. Biol 9 (5), e1003055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haswell ES, Phillips R, Rees DC, 2011. Mechanosensitive channels: what can they do and how do they do it. Structure 19, 1356–1369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hategan A, Law R, Kahn S, Discher DE, 2003. Adhesively-tensed cell membranes: lysis kinetics and atomic force microscopy probing. Biophys. J 85, 2746–2759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heidemann SR, Lamoureux P, Buxbaum RE, 1990. Growth cone behavior and production of traction force. J. Cell Biol 111 (5 (Pt 1)), 1949–1957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heidemann SR, Buxbaum RE, 1994. Mechanical tension as a regulator of axonal development. Neurotoxicology 15 (1),95–107. [PubMed] [Google Scholar]
- Heidemann SR, Lamoureux P, Buxbaum RE, 1995. Cytomechanics of axonal development. Cell Biochem. Biophys 27 (3), 135–155. [DOI] [PubMed] [Google Scholar]
- Holland MA, Miller KE, Kuhl E, 2015. Emerging brain morphologies from axonal elongation. Ann. Biomed. Eng 43, 1640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Howard J, 2001. Mechanics of Motor Proteins and the Cytoskeleton. Sinauer Associates, Inc., Sunderland, Massachusetts. [Google Scholar]
- Huang JH, Zager EL, Zhang J, Groff RF, Pfister BJ, Cohen AS, Grady MS, Maloney-Wilensky E, Smith DH, 2008. Harvested human neurons engineered as live nervous tissue constructs: implications for transplantation. Laboratory investigation. J. Neurosurg 108 (2), 343–347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang JH, Cullen DK, Browne KD, Groff R, Zhang J, Pfister BJ, Zager EL, Smith DH, 2009. Long-term survival and integration of transplanted engineered nervous tissue constructs promotes peripheral nerve regeneration. Tissue Eng. Part A 15 (7), 1677–1685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iwata A, Browne KD, Pfister BJ, Gruner JA, Smith DH, 2006. Long-term survival and outgrowth of mechanically engineered nervous tissue constructs implanted into spinal cord lesions. Tissue Eng. 12 (1), 101–110. [DOI] [PubMed] [Google Scholar]
- Lamoureux P, Heidemann SR, Martzke NR, Miller KE, 2010. Growth and elongation within and along the axon. Dev. Neurobiol 70, 135–149. [DOI] [PubMed] [Google Scholar]
- Michael TCT, Cohen SIA, Vendruscolo M, Dobson CM, Knowles TPJ, 2016. Hamiltonian dynamics of protein filament formation. Phys. Rev. Lett 116, 038101. [DOI] [PubMed] [Google Scholar]
- Nelson P, 2004. Biological Physics: Energy, Information, Life. W.H. Freeman and Company, New York. [Google Scholar]
- Nguyen TD, Hogue IB, Cung K, Purohit PK, McAlpine MC, 2013. Tension-induced neurite growth in microfluidic channels. Lab Chip 13 (18), 3735–3740. [DOI] [PubMed] [Google Scholar]
- Nixon RA, 1998. The slow axonal transport of cytoskeletal proteins. Curr. Opin. Cell Biol 10 (1),87–92. [DOI] [PubMed] [Google Scholar]
- O’Toole M, Lamoureux P, Miller KE, 2008. A physical model of axonal elongation: force, viscosity, and adhesions govern the mode of outgrowth. Biophys. J 94 (7), 2610–2620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Toole M, Miller KE, 2011. The role of stretching in slow axonal transport. Biophys. J 100, 351–360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pfister BJ, Iwata A, Meaney DF, Smith DH, 2004. Extreme stretch growth of integrated axons. J. Neurosci 24, 7978–7983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pfister BJ, Iwata A, Taylor AG, Wolf JA, Meaney DF, Smith DH, 2006. Development of transplantable nervous tissue constructs comprised of stretchgrown axons. J. Neurosci. Methods 153(1), 95–103. [DOI] [PubMed] [Google Scholar]
- Phillips R, Kondev J, Theriot J, 2009. Physical Biology of the Cell. Garland Science, New York. [Google Scholar]
- Rishal I, Fainzilber M, 2014. Axon–soma communication in neuronal injury. Nat. Rev. Neurosci 15 (1),32–42. [DOI] [PubMed] [Google Scholar]
- Samuels DC, Hentschel HG, Fine A, 1996. The origin of neuronal polarization: a model of axon formation. Philos. Trans. R. Soc. Lond. Ser. B: Biol. Sci 351 (1344), 1147–1156. [DOI] [PubMed] [Google Scholar]
- Siechen S, Yang S, Chiba A, Saif T, 2009. Mechanical tension contributes to clustering of neurotransmitter vesicles at presynaptic terminals. Proc. Natl. Acad. Sci. U. S. A 106 (31), 12611–12616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sigurdson WJ, Morris CE, 1989. Stretch-activated ion channels in growth cones of snail neurons. J. Neurosci.: Off. J. Soc. Neurosci 9 (8), 2801–2808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith DH, Wolf JA, Meaney DF, 2001. A new strategy to produce sustained growth of central nervous system axons: continuous mechanical tension. Tissue Eng. 7 (2), 131–139. [DOI] [PubMed] [Google Scholar]
- Smith DH, 2009. Stretch growth of integrated axon tracts: extremes and exploitations. Prog. Neurobiol 89 (3), 231–239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tessier-Lavigne M, Goodman CS, 1996. The molecular biology of axon guidance. Science 274 (5290), 1123–1133. [DOI] [PubMed] [Google Scholar]
- Tojkander S, Gateva G, Lappalainen P, 2012. Actin stressfibers–assembly, dynamics and biological roles. J. Cell Sci 125, 1855–1864. [DOI] [PubMed] [Google Scholar]
- Van Veen MP, Van Pelt J, 1994. Neuritic growth rate described by modeling microtubule dynamics. Bull. Math. Biol 56 (2), 249–273. [DOI] [PubMed] [Google Scholar]
- Wiggins P, Phillips R, 2005. Membrane–protein interactions in mechanosensitive channels. Biophys. J 88, 880–902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wissner-Gross ZD, Scott MA, Ku D, Ramaswamy P, Fatih Yanik M, 2011. Large-scale analysis of neurite growth dynamics on micropatterned substrates. Integr. Biol.: Quant. Biosci. Nano Macro 3 (1),65–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolf JA, Stys PK, Lusardi T, Meaney D, Smith DH, 2001. Traumatic axonal injury induces calcium influx modulated by tetrodotoxin-sensitive sodium channels. J. Neurosci 21 (6), 1923–1930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu W, Baas PW, 1994. Changes in microtubule number and length during axon differentiation. J. Neurosci 14 (5), 2818–2829. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.