Abstract
In the aftermath of stock market crash due to COVID-19, not all sectors recovered in the same way. Recently, a stock price model is proposed by Mahata et al. (2021) that describes V- and L-shaped recovery of the stocks and indices, but fails to simulate the U- and Swoosh-shaped recovery that arises due to sharp fall, continuation at the low price and followed by quick recovery, slow recovery for longer period, respectively. We propose a modified model by introducing a new parameter to quantify investors’ positive, neutral and negative sentiments, respectively. The model explains movement of sectoral indices with positive financial anti-fragility () showing U- and Swoosh-shaped recovery. Simulation using synthetic fund-flow with different shock lengths, , negative sentiment period and portion of fund-flow during recovery period show U- and Swoosh-shaped recovery. It shows that recovery of indices with positive becomes very weak with extended shock and negative sentiment period. Stocks with higher and fund-flow show quick recovery. Simulation of Nifty Bank, Nifty Financial and Nifty Realty show U-shaped recovery and Nifty IT shows Swoosh-shaped recovery. Simulation results are consistent with stock price movement. The estimated time-scale of shock and recovery of these indices are also consistent with the time duration of change of negative sentiment from the onset of COVID-19. We conclude that investors need to evaluate sentiment along with before investing in stock markets because negative sentiment can dampen the recovery even in financially anti-fragile stocks.
Keywords: COVID-19, Stock market model, Sentiment, U- and swoosh-shaped recovery, Time scale, Hilbert–Huang transform
1. Introduction
Modeling stock price dynamics is an important objective for the stock market, and a reasonably accurate prediction can result in a good profit [1]. Various models, algorithms and data mining techniques are often developed and applied to predict the behavior of stock prices [1], [2], [3], [4], [5], [6], [7], [8]. While models have been developed with parameters like return and dividend [9], [10], [11], others that adjust for seasonal stock trading are also available to create a profitable trading strategy [12]. Due to the complex nature of the stock markets, modeling the complete dynamics is very difficult [13], [14], [15], [16], [17], [18]. However, modeling the stock market dynamics to study the effect of a crisis like the COVID-19 may be possible and useful [19].
The COVID-19 pandemic shook the stock market around the globe severely [20], [21], [22], [23], [24], [25]. The panic among the investors due to the pandemic was so severe that the market crashed beyond justification within few days [25], [26], [27]. During the COVID-19 crisis, there were many quality stocks and sectors, which were resilient to the crisis and outperformed the overall market [27], [28], [29], [30], [31]. These quality stocks recovered very quickly from the crash, i.e., showing V-shaped recovery. On the other hand, many stressed stocks did not show signs of speedy recovery [26], [28].
Recently, the stock price dynamics during the COVID-19 pandemic is modeled by A. Mahata et al. [28]. They considered financial anti-fragility of the company and fund-flow by the foreign and domestic institutional investors as the main parameter and variable of the model, respectively. The parameter financial anti-fragility shows the financial strength of a company to fulfill its short term liabilities. It acts as a survival indicator of a company during a crisis. Hence, investors look for such financially anti-fragile stocks to get higher returns during a crisis [28], [29], [30], [31], [32], [33], [34]. Institutional investors also play an important role in the price movement as they are (a) responsible for huge fund inflow/outflow in the market; (b) they influence the smaller investors significantly [28], [35], [36], [37], [38], [39], [39], [40], [41], [42]. However, in the sectors like banking, finance, realty and IT, the stocks and indices even with positive financial anti-fragility took longer time to recover during the COVID-19 pandemic, i.e., they displayed U-shaped and Swoosh-shaped recovery during the prolonged COVID-19 pandemic [27]. The reason for U-shaped recovery is that after the sharp crash, many factors like Government strict measures, relaxation in loan payment, closure of construction sites lead to a prolonged drop and late recovery. The IT sector showed a Swoosh-shaped recovery as after the sharp crash, the recovery was slow due to less inflow of funds. The study of the dynamics of these recoveries are important. Hence, the model proposed by A. Mahata et al. [28] needs to be modified to describe such dynamics.
While A. Mahata et al. [28] describe the V- and L-shaped recoveries in stocks and indices, they fail to explain the U- and Swoosh-shaped recoveries in other stocks and indices. First, the V-shaped represents a sharp drop followed by a quick and almost immediate recovery. In the U-shaped, the sharp recovery after the sharp drop comes after some time. Second, the L-shaped and the Swoosh-shaped represent slow and gradual recovery after the sharp drop. In any chosen time-frame, the stocks and indices that gradually recover to the initial trend exhibits Swoosh-shape, and those that never fully recover fall into the L-shaped . We show that all the four curves can be explained if investors’ sentiment is taken into account in the model. When the COVID-19 pandemic was announced in March 2020, stock prices plummeted as panic set in, following which recoveries were witnessed. The various shapes can be understood through the details below-
-
1.
V-shaped — Financially anti-fragile stocks on which investors’ positive sentiment does not change with the crash, recovers almost immediately.
-
2.
U-shaped — Financially anti-fragile stocks on which investors’ sentiment turn negative with the crash, but recover quickly when the sentiment change into positive.
-
3.
Swoosh-shaped — Stocks on which investors’ sentiment turn negative with the crash and took some time to turn positive after easing of lockdown norms.
-
4.
L-shaped — Stocks on which investors’ sentiment turn negative with the crash and took longer time to turn neutral or somewhat positive in our chosen time frame.
In the present study, we take investors’ sentiment into account, we do not consider the V-shape and the L-shape because, for both, the investor sentiment is not expected to change within our chosen time frame.
A study on investors’ expectations following the stock market crash in March 2020 revealed that the investors largely became pessimistic about stock market returns in the short run (less than 1 year) even when their long run (10 years) expectations of the economy and stock markets remained largely unaltered [43]. A similar study on households’ stock market outlook observed that individuals who have experienced loss during past stock market crashes expect slower recovery [44]. In response to the rapid spread of the COVID-19, strict lockdown measures were implemented in different countries. These factors lead to negative sentiment among the investors, that was reflected in the stock prices of various indices and companies [20], [45]. Generally, if the sentiment of the investors remain negative, recovery becomes slow. However, announcements of certain measures by the Governments helped to change the sentiment of the investors towards the stock market that lead to the recovery [46].
In India, on 26th March 2020, the finance minister(FM) announced the Pradhan Mantri Garib Kalyan Yojana of Rs. 1.7 trillion [47], [48], [49]. On the following day, the Reserve Bank of India (RBI) reduced the repo rate by 75 basis points to 4.40 percent, lowered the cash reserve ratio by 100 basis points to 3.00 percent, and announced other measures that together aimed at injecting liquidity of Rs. 4.74 trillion into the system. On 12th May 2020, the Prime Minister announced the comprehensive Atmanirbhar package for the Indian economy that worked out to 10 percent of the Indian GDP, making it among the largest in the world [50]. The package, after including the previous announcements by the FM and the RBI, promised for a economic stimulus of Rs. 20 trillion in multiple tranches. Given the unabated spread of the COVID-19, additional relief measures of Rs. 2.65 trillion was announced on 14th November 2020. In addition to these relief measures, the decrease in the COVID cases and easing of the lockdown rules lead to the positive change in the investors sentiment that resulted in the recovery of the stock price. Hence, in order to simulate the stock price, the existing model needs to be modified to include the investor’s sentiment.
The main aim of this paper is to propose an updated model incorporating investors’ sentiment in the existing model formulated by A. Mahata et al. [28]. Our proposed model simulates the stock price movement of the sectoral indices that showed U-shaped and Swoosh-shaped recovery during the COVID-19 pandemic. We have considered the normalized net fund-flow due to institutional investors, sentiment and financial anti-fragility as the variable and parameters in the modified model, respectively. The simulation have been done for the real normalized fund-flow data () and also for artificially generated fund-flow (). The simulation results are consistent with the real stock price movement during the pandemic. We have also identified the time-scale of shock and recovery of the sectoral indices. is used to analyze the effects of different shock lengths, anti-fragility, negative sentiment lengths and fund-flow during recovery on the stock price movement.
The rest of the paper is organized as follows: Section 2 describes the model studied in this paper. Section 3 represents the technique used for the estimation of the time-scale. Section 4 represent the results obtained. Finally, we have concluded the results in Section 5.
2. Model formulation
A modified model for the stock price has been developed for the shock and recovery period during the COVID-19 pandemic. The Section 2.1 states the existing model and Section 2.2 describes the formulation of the modified model using the sentiment variable.
2.1. Existing model
A stock price model developed by A. Mahata et al. [28] can explain V-shaped and L-shaped recovery of the stock market during the COVID-19 crisis. by the foreign institutional investors and domestic institutional investors is considered as the main variable of the model. The basis for consideration of as a variable is due to the facts that institutional investors are (a) responsible for huge fund inflow/outflow in the market; (b) the influence of institutional investors on the retail investors are significant [28], [35], [36], [37], [38], [39], [39], [40], [41], [42], [51]. is defined as the difference between the fund inflow and fund outflow by the Foreign Institutional Investor (FII) and Domestic Institutional Investor (DII). Let be the net fund-flow (inflow or outflow) due to FII and DII combined at time t.
| (1) |
is the normalized net fund-flow that is used for stock price updation.
An important parameter of the model is the financial anti-fragility () which is defined as the ratio of the difference between current assets () and current liabilities () to operating expenses (). signifies the company’s ability to mitigate the current liabilities with their current assets. Current assets are those assets that can be converted in liquidity during the current operating cycle to meet up with the current liabilities. of th company is calculated as
| (2) |
The for a sectoral index can be written as
| (3) |
where is number of company in any sectoral index. acts as the control parameter for the price movement.
Finally, the model is defined as
| (4) |
| (5) |
During the shock period, the model simulation is independent of as the investors try to sell their holding irrespective of the fundamentals of the company to increase the cash holding. For Indian stocks, the value of is usually in the range .
is the coefficient of which shows the portion of net fund-flow towards a particular sector/company by the institutional investors. is different for different sectors. Though this model explains the V- and L-shaped recoveries of stocks, it fails to explain the U- and Swoosh-shaped recoveries that depends mainly on the sentiment. Sentiment-based modification is discussed below.
2.2. Modification of the existing model: Sentiment based analysis
There are many stocks with positive anti-fragility in sectors like banking, finance, realty and IT that did not show V-shaped recovery during the COVID-19 pandemic. They rather remained in L-shaped for a long period. The main reason is that the sentiment regarding these sectors remained negative or neutral for a considerable period of time because of grim business outlook and strict lockdown measures. However, the sentiment turned positive due to various measures taken by the Government. In India, different measures like decrease in repo rate and cash reserve ratio by the RBI, economic stimulus packages by the Indian Government, decrease in the COVID cases and easing of lockdown measures helped to change the sentiment positively towards the stock market. The effect of such measures in stock market is observed during the second financial quarter of 2020. After that, the above sectors rallied for a prolonged period. Hence, sentiment of the investors is one important factor that plays an important role in the stock price movement [52], [53].
The sentiment variable () can be negative sentiment, neutral sentiment and positive sentiment. When the investors are bearish towards the market or a particular sector, we assign a negative sentiment in the model. In a similar way, positive sentiment is assigned when the investors are bullish. A neutral sentiment describes a situation where the investors have no interest in the sector/company. Neutral sentiment is an ideal case as there will always be buying and selling of stocks. Mathematically, is defined as
So, the modified model can be written as
| (6) |
| (7) |
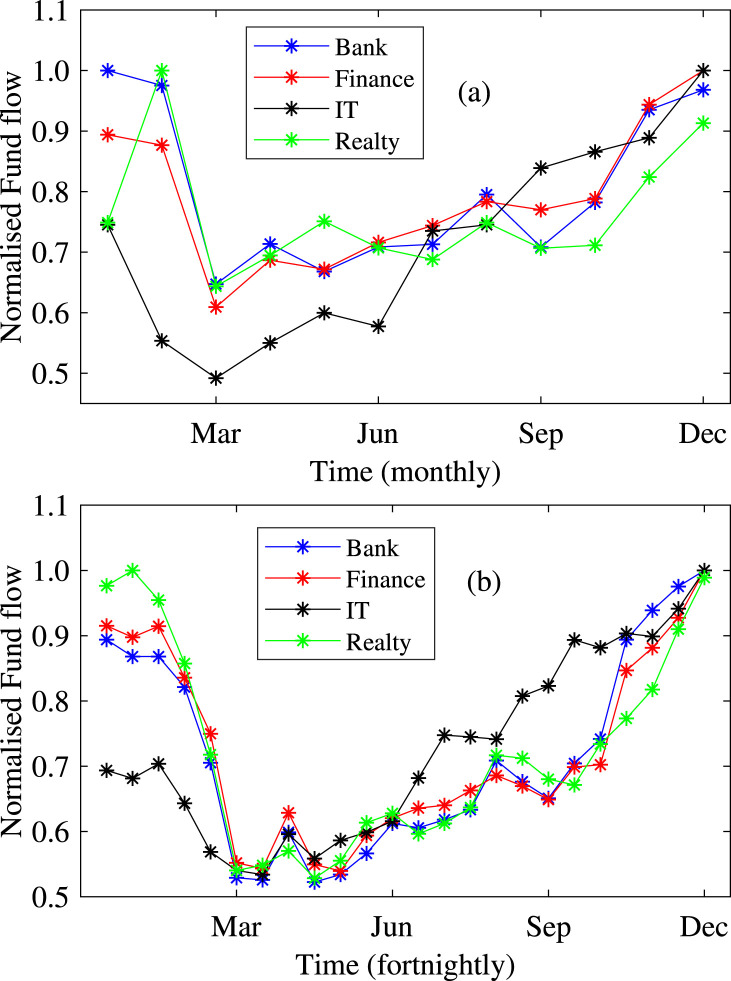
where , , are the net normalized fund-flow by the institutional investors, financial anti-fragility and coefficient of , respectively which is discussed in detail in Section 2.1. The value of is guessed on the basis of the real normalized net fund-flow due to mutual fund (MF) and foreign portfolio investor (FPI) which is shown in Fig. 1. For Indian market, the time duration of negative is from 3 months to 7 months.
Fig. 1.
Plot (a) represents the monthly data of the normalized fund-flow due to mutual fund in the Bank, Finance, Realty and Information Technology (IT) sectors. Plot (b) represents the fortnightly data of the normalized fund-flow due to FPI in the Bank, Finance, Realty and Information Technology (IT) sectors.
In Section 4.1, we have simulated the stock price movement from Eqs. (6)–(7) using to study the dynamics of stock price during COVID like shocks. Further, in Section 4.2, we have studied the stock price dynamics using the and of the sectoral indices in Eqs. (6)–(7).
2.2.1. COVID-like shock
In order to understand the effect of COVID like crisis on the stock price, we need to study the model under different shock lengths (), negative sentiment lengths (), financial anti-fragility () and fund-flow during the recovery period. We have divided the fund-flow distribution into five segments, i.e., normal, shock, negative sentiment, recovery and post recovery periods. We have taken the distribution of for those periods as , , , , and , respectively. The distribution is similar to the distribution of real fund-flow data. The values of are chosen from Fig. 1 in ad-hoc basis depending on the portion of fund-flow in various sectors. In the present study, the values of during normal, shock, negative sentiment, recovery and post recovery period are , respectively.
In order to understand the U-shaped and Swoosh-shaped recovery of stocks during different crisis, we have carried out the simulation considering different possibilities. Firstly, we have fixed and period of negative sentiment, day (D), and varied D, 30 D, 45 D, and 60 D, respectively. Secondly, for fix D and D, ’s are varied as and 1.2. Thirdly, we have varied the negative sentiment periods as D, 50 D, 75 D, and keeping and D. Finally, we have varied the fund-flow during the recovery period by changing the value as keeping , and at 0.9, 25 D and 0 D, respectively. The detailed analyses results are discussed in Section 4.1.
2.2.2. COVID-19 shock
The model simulation of stock price during the COVID-19 has been done considering , and for the Indian stock market. represents the sentiment of the investors. is the real net normalized fund-flow due to the institutional investors. The daily fund-flow data is available in the Moneycontrol website [54]. of a company is estimated using Eq. (2). The current assets, current liabilities and operating expenses are taken from the financial report of a company that is available in Bombay Stock Exchange Ltd [55].
The coefficient is estimated from the fund-flow to a particular sector due to the DIIs and Foreign portfolio investors (FPIs). In this study, the sectoral fund-flow data due to Mutual fund investor (MFI) is taken as DII data. Fig. 1(a) represents the MFI normalized monthly fund-flow in Realty (Green), Information Technology (Black), Finance (Red) and Bank (Blue). These sectoral fund-flow data are obtained from Securities and Exchange Board of India (SEBI) [56]. Fig. 1(b) represents the FPI normalized fortnightly fund-flow in Realty (Green), Information Technology (Black), Finance (Red) and Bank (Blue). The data are taken from National Securities Depository Ltd. (NSDL), India [57]. The plots clearly show that the fund-flow decreased drastically during the onset of the COVID-19 pandemic. It shows that after the crash, the infusion of funds was not rapid in the above sectors. This indicates that the investors are cautious to invest in these sectors. Further, the plots show that the fund-flow in the IT sector increased gradually compared to the other sectors. The inflow of funds may be due to the change in sentiment from bearish to bullish as compared to other sectors. The sectors like Bank, Finance and Realty took longer time to recover due to less inflow of funds. The main reason of less fund-flow in these sectors is negative sentiment. Considering the proportionality of fund-flow in various sectors, we have chosen the value of as for the Nifty Bank, for the Nifty Financial and for the Nifty Realty during pre-covid, shock, negative sentiment, recovery and post recovery period, respectively. As there was no negative sentiment towards the Nifty IT, we have chosen for pre-covid, shock, recovery and post recovery period, respectively. The results of the analysis is given in Section 4.2.
The negative sentiment in banking, finance, realty sectors during the COVID-19 pandemic can be confirmed by estimating the time scales of shock and recovery of these sectors. The time scale of shock and recovery of the IT sector is also calculated to confirm that it did not have a negative sentiment, but its recovery was not swift. Section 3 describes the technique used in the calculation of the time-scale of the above sectoral indices. The results of the time-scale analysis is given in Section 4.3.
3. Techniques for time-scale analysis
In order to identify and analyze the different relevant time-scales () that our data-set inherits, we employ the Hilbert–Huang transform (HHT) [58]. HHT consists of two parts; (a) Empirical mode decomposition (EMD) and (b) Hilbert spectrum. For a time-series that is either stationary or linear, its intrinsic time-scale can easily be computed. In the face of non-stationary and nonlinear behavior presented by the data, such an inference becomes non-trivial. It is evident that our stock-market data is far from being adherent to the assumptions of linearity and weak-stationarity; see [15], [58] for the assumptions. Empirical mode decomposition is one of the handful of successful data analysis tools available for such time-series data. In this subsection, we give a very brief overview of how the method has been designed to work, along with a statistical treatment to discern which intrinsic time-scales are particularly relevant and statistically significant.
3.1. Empirical mode decomposition (EMD)
As discussed in [58], the EMD method uses the sifting process to decompose an empirical time-series into simple oscillatory modes, each of them is called an intrinsic mode function (IMF).
More specifically, one can write
where is the th IMF and is the residue which is usually a monotone function capturing the average trend of the data. Each IMF satisfies to following properties:
-
1.
In the entire data-set, the number of extrema (maxima and minima) and zero crossings should be equal or differ by one, and
-
2.
At any point, the mean value of the envelope defined by the local maxima and the envelope defined by the local minima should be zero.
For more details on the sifting process and the mathematical properties of IMFs, the reader is encouraged to consult [58].
Despite the analogy with simple oscillations, an IMF can have time-varying amplitude and frequency. The instantaneous frequency of any IMF, , can be computed using its Hilbert transform:
where denotes the Cauchy principal value of the integral. By the nature of Hilbert transform, we can have an analytic signal,
where
The instantaneous frequency of the IMF is then calculated by: . To each IMF, we can also associate its time-scale by averaging over the entire data length. The time-scale of IMFs are particularly important to identify relevant events, such as shock, recovery, etc., and their persistence. It is worth noting that the sifting process picks out the IMFs in the increasing order of their time-scale.
3.2. Statistical significance test (SST)
Our analysis also entails a statistical treatment of the data-set, assuming that our data might be erroneous. As with any physical signal, the true stock-price data is also inevitably mixed with different types of noise. The non-linear and non-stationary nature of the data makes it difficult to filter the noise from the true signal. However, we can assign statistical significance to the computed IMFs to decide whether they are just white noise, or they really carry some information/trend [59], [60]. To build context for comparison, we follow [59] to briefly discuss the probability distribution of the IMFs and their energy density, when computed from white noise.
The energy density of the th IMF, , is defined by
where denotes the number of data points. We also define the notion of mean period of to be the number of local maxima and diving it by , the total length. As empirically observed in [59], the IMFs (except for ) from a normalized Gaussian white noise data-set have the identical spectral shape in terms of the -axis. The observation leads to the following relation for the th IMF () of a Gaussian white noise series:
| (8) |
where
is the spectrum-weighted mean period and is the mean energy density. For very large , the and are good estimators of and , respectively.
Using Eq. (8), the probability distribution of the energy density of the IMFs of a Gaussian white noise data-set is also established. The distribution of has been shown to approximately follow , where . As a consequence, one can derive the energy spread lines at different level of significance using the following formula:
where a for 99% confidence interval as an example. The pair for the th IMF that contains information is expected to lie outside the spread lines at 99% confidence level [59].
4. Results and discussion
We have presented the simulation result of COVID-like shock using in Section 4.1. In Section 4.2, we analyze the simulated stock price obtained using during the COVID-19 pandemic for the (1) Nifty Bank, (2) Nifty Financial, (3) Nifty Realty and (4) Nifty IT. The result of time-scale analysis of these indices is presented in Section 4.3. The daily stock price data are downloaded for the period of 1st July 2019 to 31st May 2021 from NSE website [61].
4.1. Simulation of COVID-like shock
Fig. 2(a) represents the plot of U-shaped recovery of stock price for different using for a fix =25 D and =130 D. The plots show the simulated stock price for in red, green, blue and black color, respectively. During the negative sentiment period, they did not show any signs of recovery even though . When the sentiment becomes positive, the stocks with positive starts recovering. The figure shows that the stocks with the highest recovers rapidly and outperforms its peer. The rate of recovery decreases with decrease in the value of . These analyses show that the recovery rate directly depends on the when the sentiment is positive.
Fig. 2.
Plot (a) shows the U-shaped recovery using synthetic data for fixed and and 1.2. Plot (b) represents the Swoosh-shaped recovery for fixed , and during the recovery period. represents day and represents the financial anti-fragility. For the simulation, initial condition is taken as 0.5.
In order to understand the Swoosh-shaped recovery, we have considered , and . Fig. 2(b) represents the Swoosh-shaped recovery for different portion of fund allocated () during the recovery period. The plots in red, green, blue and black represent the stock price for as 0.05, 0.15, 0.25 and 0.35 during the recovery period, respectively. The figure shows that when there is no negative sentiment, price starts recovering after the shock period is over. The recovery depends only on the fund-flow by the investors. Fig. 2(b) shows that the stock with highest , i.e., 0.35 recovers rapidly. The recovery of stocks with is slow. The rate of recovery is directly proportional to the fund-flow. Hence, the recovery not only depends on the sentiment but is also dependent on the portion of fund allocated.
Fig. 3(a) represents the U-shaped recovery for different with and . The plots show the simulated stock price for in red, green, blue and black, respectively. The figure shows that the stocks with shortest shock length, i.e., recovers quickly to its initial level after the sentiment turns positive. An extended will also affect the recovery period. The stock with the least will have maximum recovery period. The recovery period will decrease as the increases. This is clearly seen in Fig. 3(a) for stocks with . Hence, the recovery of positive stocks also gets affected with the increase in .
Fig. 3.
Plot (a) represents the U-shaped recovery using the synthetic data for fixed and and . Plot (b) represents the U-shaped recovery using synthetic fund-flow data for fixed and with and . For the simulation, initial condition is taken as 0.5. and represent day and financial anti-fragility.
Fig. 3(b) represents the U-shaped recovery for different with and . The plots show the simulated stock price for in red, green, blue and black, respectively. The figure shows that for a fix , the recovery of stocks depend on the . Fig. 3(b) shows that the stocks with shows faster recovery than the stocks with . The recovery starts only after the sentiment becomes positive. A long affects the recovery period which can be seen in Fig. 3(b). The recovery period decreases with an increase in . It clearly shows that the sentiment of the investors is very important for the stocks to recover. Until the sentiment becomes positive, no fundamentally strong company can recover and performs well. It is important to mention that the V-shaped and L-shaped recovery of stocks as mentioned in Ref. [28] can be reproduced by taking in the modified model.
4.2. Simulation of the COVID-19 shock
Figs. 4(a) and 4(b) represent the model simulated stock price ( line) using and original stock price (solid line) of the Nifty Bank and Nifty Financial, respectively during the COVID-19 pandemic. The simulation results show that the stock price crash started from the 1st week of March 2020 and fell for around 20-25 D till 1st week of April 2020. After a severe crash, they did not show the signs of recovery for a considerable period as the investors had a very bearish/negative sentiment towards these sectors. Hence, these stocks could not recover though they were financially anti-fragile. In order to give a boost to reviving the economy, the Indian government announced a COVID relief package of Rs. 20 trillion on May 12, 2020 [47]. This amount was to be invested in different sectors in different tranches including a special liquidity facility for Mutual Funds for Rs. 50,000 crore. The stock market’s sentiment turned bullish, however, this sentiment did not last for long in the banking and financial sectors. Though, a slight recovery during the month of May is seen in these sectors due to the change of sentiment of the investors which is captured in both Original and Simulated stock price as shown in Fig. 4(a) and 4(b). From the 4th week of September 2020, strong recoveries in these sectors were seen due to the positive sentiment of the investors. During this period, the fund inflow towards these sectors was increased significantly as shown in Fig. 1. The inflow of funds may also be due to the expectation of the investors that the government might announce some stimulus package for the recovery of economy. The government’s announcement of a stimulus package of Rs. 2.65 lakh crore during the 2nd week of November 2020 [48] and the decrease in the number of COVID cases made the investors even more bullish. As a result, there was regular inflow of funds which lead to the recovery of these sectors. The model simulation shows a U-shaped recovery which is consistent with the original stock price movement of the Nifty Bank and Nifty Financial. It may be due to the negative sentiment of the investors that led to these financially strong sectors for U-shaped recovery.
Fig. 4.
Plot (a) represents the original stock price movement of the Nifty Bank (  ) and its corresponding model simulated stock price movement () with and . Plot (b) represents the original stock price movement of Nifty Financials (
) and its corresponding model simulated stock price movement () with and . Plot (b) represents the original stock price movement of Nifty Financials (  ) and its corresponding model simulated stock price movement () with and .
) and its corresponding model simulated stock price movement () with and .
Figs. 5(a) and 5(b) represent the original stock price (solid line) and simulated price (line) for the Nifty IT and Nifty Realty, respectively. Fig. 5(a) shows that after the shock period, the IT sector recovers slowly showing Swoosh-shaped recovery. Though there was no negative sentiment towards IT sectors, the fund-flow in this sector was less compared to the Pharma and FMCG sectors [28]. As a result, we have seen slow recovery in the IT sector. Fig. 5(a) shows that there is some deviation between simulated and original stock price during the months of August–September 2020. During this period, was negative though the fund-flow towards the IT sector was positive [ Fig. 1]. Simulation using may have created such deviation. Similar to the Nifty Bank and Nifty Financial, the Nifty Realty also shows U-shaped recovery as seen in Fig. 5(b). Though the stocks with U-shaped showed some initial recovery during the month of May 2020 due to the announcement of COVID relief package, the sentiment of investors did not last long. Hence, their recovery did not last long as seen in Fig. 5(b). A steady recovery was seen from the month of November 2020 due to the stimulus package announcement by the Indian government and decrease in the COVID cases in India. These reasons lead to the change of the sentiment which resulted in the steady recovery of stock price.
Fig. 5.
Plot (a) shows the original stock price movement of the Nifty IT(  ) and its corresponding model simulated stock price movement () with and . Similarly, plot (b) shows the original stock price movement of Nifty Realty (
) and its corresponding model simulated stock price movement () with and . Similarly, plot (b) shows the original stock price movement of Nifty Realty (  ) and its corresponding model simulated stock price movement () with and .
) and its corresponding model simulated stock price movement () with and .
We have also calculated the correlation coefficient () between original stock price and the simulated stock price which is shown in Table 1. values show that there is a high correlation between the real data and our model simulated data for all the four sectors. The -value is also calculated for the same which is within a 95% confidence level, i.e., less than 0.05.
Table 1.
The table shows the correlation coefficient () and the -value between the Original data (OD) and the simulated data (SD).
| Nifty bank | Nifty financial | Nifty realty | Nifty IT | |
|---|---|---|---|---|
| P-val | ||||
| 0.930 | 0.911 | 0.848 | 0.948 |
These analyses show that the stock price recovers only after the sentiment becomes positive. It shows that the reasons for change in sentiment should be monitored carefully even though the sectors or stocks are financially anti-fragile. Investors should monitor the change in the sentiment to enter in the stocks for investment or trading. The analyses of COVID-like crisis may help the investors to plan their investments during different crises. The model simulation is consistent with the real stock price movement during the COVID-19 pandemic. Hence, the model will be helpful to identify and explain certain complex behavior such as crash, recovery and negative sentiment period in the stock market. It is pertinent to mention that due to the unavailability of the daily fund-flow data, we are unable to simulate other stock markets. Hope this model may also be able to simulate other stock markets.
4.3. Time-scale analysis
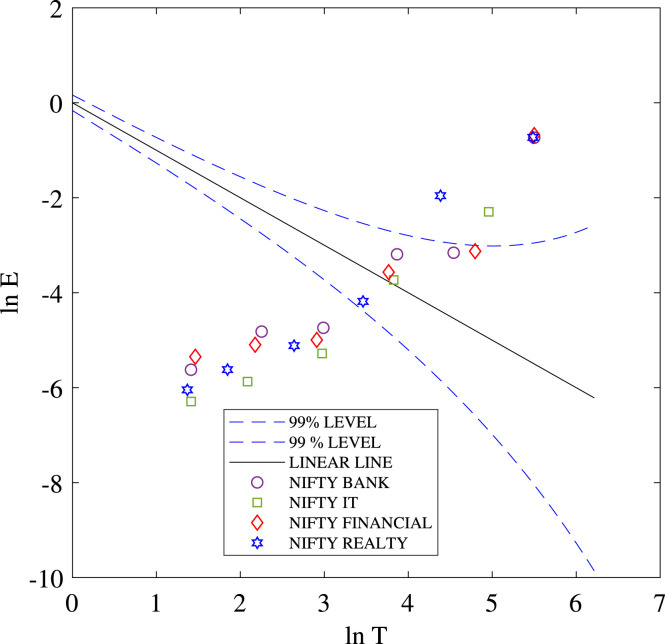
HHT technique is applied to calculate the time-scale () of shock and recovery of sectoral indices during the COVID-19 pandemic. Fig. 6 represents the original data (OD) of the Nifty Bank, its six IMFs and residue obtained from the EMD technique. The residue represents the overall trend of the OD. A statistical significance test (SST) of the decomposed IMFs of all the indices are carried out and are represented in Fig. 7. The plot shows the SST at 99% significance level. IMFs which lie within the significance level may contain noise. In case of Nifty Bank and Nifty Financial all the IMFs contain information except IMF4 and IMF5, i.e., IMF4 and IMF5 are inside the significance level. For Nifty IT, IMF4 lies within the significance level and for Nifty Realty, IMF5 is within the confidence level.
Fig. 6.
Plot represents the original data (OD) of the Nifty Bank and its -. Residue represents the overall trend of the original data.
Fig. 7.
Plot represents the significance test of the IMFs of the Nifty Bank, Nifty Financials, Nifty Realty and Nifty IT sectoral indices with 99% significance level.
We have calculated the , i.e., time-scale from shock till recovery, of U-shaped and Swoosh-shaped sectoral indices during the COVID-19 by identifying the dominant IMF. For this, we have calculated the correlation coefficient () and -value between the original stock price and all the IMFs. Table 2 contains the , and -value of all the IMFs. Considering this, and the result of the SST we have identified the dominant IMF. Figs. 8(a)–8(d) represent the original data (solid line) and their dominant IMF ( line) of Nifty IT, Nifty Bank, Nifty Financial and Nifty Realty, respectively. In case of the Nifty Bank, Nifty Financial and Nifty Realty, IMF6 is the dominant IMF and for the Nifty IT, IMF5 is dominant. The estimated for Nifty IT, Nifty Bank, Nifty Financial and Nifty Realty are 142 D, 244 D, 244 D and 241 D, respectively. The obtained ’s are consistent with the real time taken by the indices to recover during the COVID-19 pandemic.
Table 2.
Measure of events correlation coefficient () between original data (OD) and its IMFs. Significance test of the correlation coefficient of all the IMFs with the OD have been performed. shows the maximum correlation with the OD for Nifty Bank, Nifty Financial and Nifty Realty, whereas, in case of Nifty IT gives maximum correlation. The -value of the are also calculated for all the four indices. represents the time-scale of the shock and recovery in days (D)
| IMF | Nifty bank |
Nifty financial |
Nifty realty |
Nifty IT |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P-val | P-val | P-val | P-val | |||||||||
| IMF1 | 4 | 0.095 | 0.102 | 4 | 0.189 | 0.079 | 4 | 0.503 | 0.040 | 4 | 0.462 | 0.057 |
| IMF2 | 10 | 0.311 | 9 | 0.253 | 0.0696 | 6 | 0.712 | 0.023 | 8 | 0.525 | 0.0488 | |
| IMF3 | 20 | 0.011 | 0.153 | 18 | 0.159 | 0.086 | 14 | 0.741 | 0.020 | 20 | 0.990 | −0.001 |
| IMF4 | 48 | 0.020 | 0.141 | 43 | 0.215 | 32 | 0.086 | 0.104 | 46 | 0.041 | 0.156 | |
| IMF5 | 94 | 0.012 | 0.152 | 121 | 0.003 | 0.177 | 80 | 0.166 | 0.084 | 142 | 0.804 | |
| IMF6 | 245 | 0.912 | 245 | 0.919 | 241 | 0.819 | ||||||
Fig. 8.
Plot (a), (b), (c) and (d) represent the original data (  line) and its dominant IMF ( line) of the Nifty IT, Nifty Bank, Nifty Financials and Nifty Realty, respectively.
line) and its dominant IMF ( line) of the Nifty IT, Nifty Bank, Nifty Financials and Nifty Realty, respectively.
5. Conclusion
In this paper, we have modified an existing model of stock price dynamics to explain the U-shaped and Swoosh-shaped recovery during the COVID-19 pandemic. In our simulation, we have considered net fund-flow by the institutional investors () as the main variable, and financially anti-fragility () and sentiment of the investors () as the main parameters. In our simulation, we have considered that stock price crash is totally governed by . Whereas, and are important parameters during the recovery of stock price. The model simulates the stock price considering different , , and during the recovery period. The model simulated result and the real stock price are also consistent during the COVID-19 pandemic. We have also identified the from the original data using the HHT technique.
We have obtained U-shaped recovery of stocks for using the synthetic fund-flow data () with and . After the sentiment of the investor changes to positive, the stock with a higher outperforms the others. We have also obtained U-shaped recovery of stocks with for different . When and , the stock price recovers to its pre-shock value after the is over. However, with an extended the recovery of positive stocks also becomes difficult. The recovery of stock under different is also studied. We have obtained U-shaped recovery for different with and . The stock price recovers for and showing U-shaped recovery. When the is extended beyond 50 D the recovery of positive stocks also becomes difficult. Lastly, we have obtained Swoosh-shaped recovery of stocks for different values during the recovery period with , and . When the stock price recovers to its pre-COVID price showing Swoosh-shaped recovery. However, for the recovery is very slow. With the decrease in value during recovery, the rate of recovery also decreases.
We have obtained U-shaped and Swoosh-shaped recovery of stock price from the model simulation using the real normalized net fund-flow data (). We have calculated the for Bank, Financial, Realty and IT sectoral indices. The Nifty Realty, Nifty Bank, Nifty Financial show U-shaped recovery from our simulation result and Nifty IT shows a Swoosh-shaped recovery. We observe that the model simulation results are consistent with the real stock price movement. Finally, we have estimated the for the above indices and they are consistent with the real time taken by these indices to recover during the COVID-19 pandemic. This study shows that the stock price recovers when the sentiment becomes positive. We conclude that investors, especially who are risk-aversive, will need to evaluate sentiment along with financial anti-fragility before investing in the stock markets because negative sentiment can dampen the recovery even in the financially anti-fragile stocks. Thus, this study may help the investors to take investment decisions during crisis.
CRediT authorship contribution statement
Anish Rai: Conceptualization, Writing – original draft, Software, Validation, Formal analysis, Resources. Ajit Mahata: Formal analysis, Methodology, Investigation, Resources, Validation. Md Nurujjaman: Supervision, Conceptualization, Writing – original draft, Software, Validation, Formal analysis, Resources. Sushovan Majhi: Writing – original draft, Methodology, Validation, Formal analysis. Kanish Debnath: Writing – original draft, Validation, Formal analysis.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
We would like to thank Om Prakash, Salam Rabindrajit Luwang and Sandeep Parajuli for their help in data analysis. NIT Sikkim is appreciated for allocating doctoral research fellowships to A.R. and A.M.
References
- 1.Ballings M., Van den Poel D., Hespeels N., Gryp R. Evaluating multiple classifiers for stock price direction prediction. Expert Syst. Appl. 2015;42(20):7046–7056. [Google Scholar]
- 2.Naimzada A., Pireddu M. A financial market model with endogenous fundamental values through imitative behavior. Chaos. 2015;25(7) doi: 10.1063/1.4926326. [DOI] [PubMed] [Google Scholar]
- 3.Naimzada A., Pireddu M. Introducing a price variation limiter mechanism into a behavioral financial market model. Chaos. 2015;25(8) doi: 10.1063/1.4927831. [DOI] [PubMed] [Google Scholar]
- 4.Barak S., Modarres M. Developing an approach to evaluate stocks by forecasting effective features with data mining methods. Expert Syst. Appl. 2015;42(3):1325–1339. [Google Scholar]
- 5.Ou P., Wang H. Prediction of stock market index movement by ten data mining techniques. Modern Appl. Sci. 2009;3(12):28–42. [Google Scholar]
- 6.Oh K.J., Kim K.-j. Analyzing stock market tick data using piecewise nonlinear model. Expert Syst. Appl. 2002;22(3):249–255. [Google Scholar]
- 7.Huang W., Nakamori Y., Wang S.-Y. Forecasting stock market movement direction with support vector machine. Comput. Oper. Res. 2005;32(10):2513–2522. [Google Scholar]
- 8.Kim K.-j. Financial time series forecasting using support vector machines. Neurocomputing. 2003;55(1–2):307–319. [Google Scholar]
- 9.Ding Z., Granger C.W., Engle R.F. A long memory property of stock market returns and a new model. J. Empir. Financ. 1993;1(1):83–106. [Google Scholar]
- 10.Marsh T.A., Merton R.C. Dividend behavior for the aggregate stock market. J. Bus. 1987;60(1):1–40. [Google Scholar]
- 11.Marsh T.A., Merton R.C. Dividend variability and variance bounds tests for the rationality of stock market prices. Am. Econ. Rev. 1986;76(3):483–498. [Google Scholar]
- 12.Booth A., Gerding E., McGroarty F. Automated trading with performance weighted random forests and seasonality. Expert Syst. Appl. 2014;41(8):3651–3661. [Google Scholar]
- 13.Kwapień J., Drożdż S. Physical approach to complex systems. Phys. Rep. 2012;515(3–4):115–226. [Google Scholar]
- 14.Mantegna R.N., Stanley H.E. Cambridge University Press; 1999. Introduction To Econophysics: Correlations and Complexity in Finance. [Google Scholar]
- 15.Huang N.E., Wu M.-L., Qu W., Long S.R., Shen S.S. Applications of Hilbert–Huang transform to non-stationary financial time series analysis. Appl. Stoch. Models Bus. Ind. 2003;19(3):245–268. [Google Scholar]
- 16.Nurujjaman M., Mahata A. Time scales and characteristics of stock markets in different investment horizons. Front. Phys. 2020;8:498. [Google Scholar]
- 17.Sornette D. Princeton University Press; 2009. Why Stock Markets Crash. [Google Scholar]
- 18.Mahata A., Bal D.P., Nurujjaman M. Identification of short-term and long-term time scales in stock markets and effect of structural break. Physica A. 2020;545 [Google Scholar]
- 19.Charles A., Darné O. Large shocks in the volatility of the Dow Jones Industrial Average index: 1928–2013. J. Bank. Financ. 2014;43:188–199. [Google Scholar]
- 20.Ashraf B.N. Economic impact of government interventions during the COVID-19 pandemic: International evidence from financial markets. J. Behav. Exp. Finance. 2020;27 doi: 10.1016/j.jbef.2020.100371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Topcu M., Gulal O.S. The impact of COVID-19 on emerging stock markets. Finance Res. Lett. 2020;36 doi: 10.1016/j.frl.2020.101691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Baker S.R., Bloom N., Davis S.J., Kost K., Sammon M., Viratyosin T. The unprecedented stock market reaction to COVID-19. Rev. Asset Pricing Stud. 2020;10(4):742–758. [Google Scholar]
- 23.Zhang D., Hu M., Ji Q. Financial markets under the global pandemic of COVID-19. Finance Res. Lett. 2020;36 doi: 10.1016/j.frl.2020.101528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.https://www.bbc.com/news/business-51796806.
- 25.Rai A., Mahata A., Nurujjaman M., Prakash O. Statistical properties of the aftershocks of stock market crashes revisited: Analysis based on the 1987 crash, financial-crisis-2008 and COVID-19 pandemic. Internat. J. Modern Phys. C. 2021 [Google Scholar]
- 26.Mahata A., Rai A., Nurujjaman M., Prakash O., Prasad Bal D. Characteristics of 2020 stock market crash: The COVID-19 induced extreme event. Chaos. 2021;31(5) doi: 10.1063/5.0046704. [DOI] [PubMed] [Google Scholar]
- 27.Mazur M., Dang M., Vega M. COVID-19 And the march 2020 stock market crash. Evidence from S&P1500. Finance Res. Lett. 2021;38 doi: 10.1016/j.frl.2020.101690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Mahata A., Rai A., Nurujjaman M., Prakash O. Modeling and analysis of the effect of COVID-19 on the stock price: V and L-shape recovery. Physica A. 2021;574 doi: 10.1016/j.physa.2021.126008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Asness C.S., Frazzini A., Pedersen L.H. Quality minus junk. Rev. Account. Stud. 2019;24(1):34–112. [Google Scholar]
- 30.Bouchaud J.-P., Ciliberti S., Landier A., Simon G., Thesmar D. 2016. The excess returns of“ quality” stocks: a behavioral anomaly. arXiv preprint arXiv:1601.04478. [Google Scholar]
- 31.Novy-Marx R. The other side of value: The gross profitability premium. J. Financ. Econ. 2013;108(1):1–28. [Google Scholar]
- 32.Castro N.R., Chousa J.P.n. An integrated framework for the financial analysis of sustainability. Bus. Strategy Environ. 2006;15(5):322–333. [Google Scholar]
- 33.Lee D.D., Faff R.W. Corporate sustainability performance and idiosyncratic risk: A global perspective. Financ. Rev. 2009;44(2):213–237. [Google Scholar]
- 34.https://www.wsj.com/articles/investors-rush-into-quality-stocks-11570413961.
- 35.Cao C., Chang E.C., Wang Y. An empirical analysis of the dynamic relationship between mutual fund flow and market return volatility. J. Bank. Financ. 2008;32(10):2111–2123. [Google Scholar]
- 36.Coval J., Stafford E. Asset fire sales (and purchases) in equity markets. J. Financ. Econ. 2007;86(2):479–512. [Google Scholar]
- 37.Ülkü N., Weber E. Identifying the interaction between foreign investor flows and emerging stock market returns. Rev. Finance. 2014;18(4):1541–1581. [Google Scholar]
- 38.Kling G., Gao L. Chinese institutional investors’ sentiment. J. Int. Financ. Mark. Inst. Money. 2008;18(4):374–387. [Google Scholar]
- 39.Edelen R.M., Warner J.B. Aggregate price effects of institutional trading: a study of mutual fund flow and market returns. J. Financ. Econ. 2001;59(2):195–220. [Google Scholar]
- 40.KP P. Dynamics of foreign portfolio investment and stock market returns during the COVID-19 pandemic: Evidence from India. Asian Econ. Lett. 2020;1(2) doi: 10.46557/001c.17658. [DOI] [Google Scholar]
- 41.Edelen R.M. Investor flows and the assessed performance of open-end mutual funds. J. Financ. Econ. 1999;53(3):439–466. [Google Scholar]
- 42.Warther V.A. Aggregate mutual fund flows and security returns. J. Financ. Econ. 1995;39(2–3):209–235. [Google Scholar]
- 43.Giglio S., Maggiori M., Stroebel J., Utkus S. The joint dynamics of investor beliefs and trading during the COVID-19 crash. Proc. Natl. Acad. Sci. 2021;118(4) doi: 10.1073/pnas.2010316118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Hanspal T., Weber A., Wohlfart J. Exposure to the COVID-19 stock market crash and its effect on household expectations. Rev. Econ. Stat. 2020:1–45. [Google Scholar]
- 45.Alexakis C., Eleftheriou K., Patsoulis P. COVID-19 Containment measures and stock market returns: An international spatial econometrics investigation. J. Behav. Exp. Finance. 2021;29 doi: 10.1016/j.jbef.2020.100428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Narayan P.K., Phan D.H.B., Liu G. COVID-19 Lockdowns, stimulus packages, travel bans, and stock returns. Finance Res. Lett. 2021;38 doi: 10.1016/j.frl.2020.101732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.https://indianexpress.com/article/explained/atmanirbhar-package-full-break-up-of-rs-20-lakh-crore-nirmala-sitharaman-lockdown-6414044/.
- 48.https://home.kpmg/xx/en/home/insights/2020/04/india-government-and-institution-measures-in-response-to-covid.html.
- 49.Ghosh J. A critique of the Indian government’s response to the COVID-19 pandemic. J. Ind. Bus. Econ. 2020;47(3):519–530. [Google Scholar]
- 50.https://economictimes.indiatimes.com/news/economy/finance/latest-stimulus-package-among-largest-in-the-world/articleshow/75701976.cms.
- 51.Barber B.M., Odean T., Zhu N. Do retail trades move markets? Rev. Financ. Stud. 2008;22(1):151–186. [Google Scholar]
- 52.Guo K., Sun Y., Qian X. Can investor sentiment be used to predict the stock price? Dynamic analysis based on China stock market. Physica A. 2017;469:390–396. [Google Scholar]
- 53.Baker M., Wurgler J. Investor sentiment and the cross-section of stock returns. J. Finance. 2006;61(4):1645–1680. [Google Scholar]
- 54.https://www.moneycontrol.com/.
- 55.https://www.bseindia.com/.
- 56.https://www.sebi.gov.in/.
- 57.https://nsdl.co.in/.
- 58.Huang N.E., Shen Z., Long S.R., Wu M.C., Shih H.H., Zheng Q., Yen N.-C., Tung C.C., Liu H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998;454(1971):903–995. [Google Scholar]
- 59.Wu Z., Huang N.E. A study of the characteristics of white noise using the empirical mode decomposition method. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2004;460(2046):1597–1611. [Google Scholar]
- 60.Wu Z., Huang N.E. Hilbert-Huang Transform and Its Applications. World Scientific; 2005. Statistical significance test of intrinsic mode functions; pp. 107–127. [Google Scholar]
- 61.https://www1.nseindia.com/.