FIGURE 3.

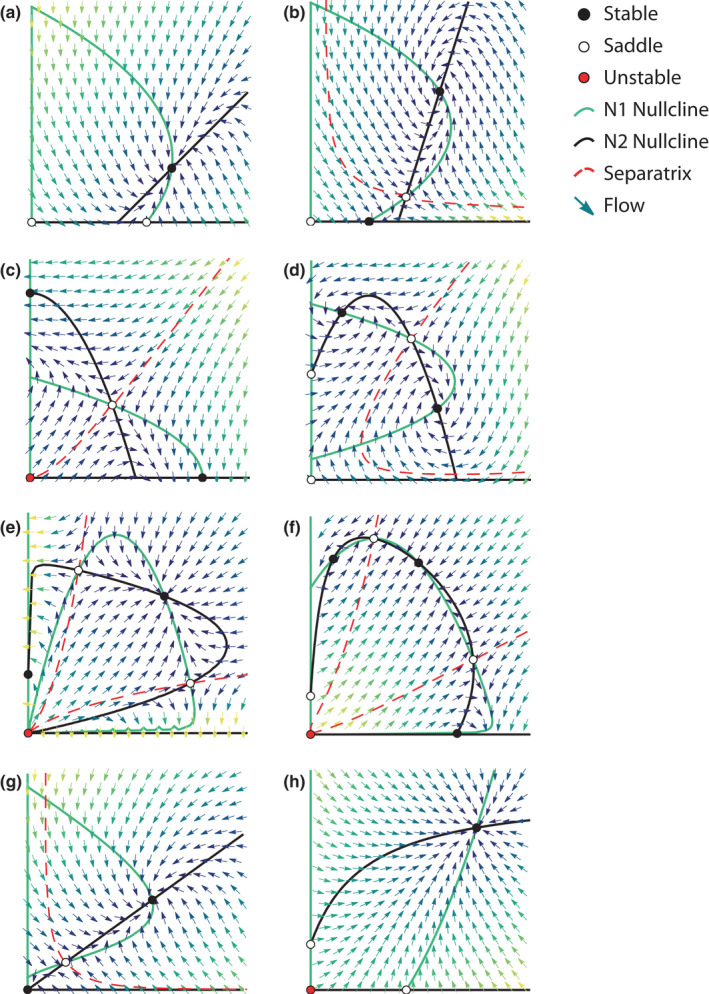
Characteristic dynamics for shifting net effects and consumer‐resource models. Models that investigated shifts in net effects as a balance of costs and benefits (“context‐dependency”) led to a synthesis of mutualism into a consumer‐resource framework. Models with saturating benefit functions and linear costs (a‐b) tend to display stable coexistence (a) and threshold effects (b) like earlier models (Figure 2). Stable coexistence is “mutualistic” if the nullclines intersect such that both species achieve higher density than they would alone, or if increasing the density of one species from equilibrium permit growth of its partner. Otherwise, the interaction is “parasitic.” Linear costs can make the coexistence equilibrium a stable spiral, with damped oscillations toward equilibrium (b, d, f, g). Models with unimodal benefit response that allow negative effects (net costs) at high density (c, d) or that include both separately saturating costs and benefits (e, f) display more complex dynamics. Depending on its parameterization, the mutualism‐competition model by Zhang (2003) displays mutualistic stable coexistence (not shown), competitive exclusion (c), or competitive dominance (d), with dominant species dependent on initial densities (i.e., system initialized to the left or right of the separatrix). The consumer‐resource model by Holland and DeAngelis (2010) also displays a range of dynamics depending on parameterization (e, f), including multiple stable coexistence equilibria (f). Mutualistic coexistence occurs when the ratio of consumers to their resources is not above a certain threshold (i.e., to the left of the left separatrix, or below the bottom separatrix). Otherwise, consumers overexploit their resources (causing more costs than provided benefits), leading to system collapse. Recent works use a consumer‐resource approach with system‐specific mechanisms (g, h), but often exhibit the simpler qualitative dynamics of saturating benefit models (Figure 2) with the potential for oscillations (g). Panels show the following models: (a–b) Neuhauser & Fargione, 2004, plant‐mycorrhizae; (c, d) Zhang, 2003, competitor‐mutualists; (e, f) Holland & DeAngelis, 2010, bidirectional consumer‐resource mutualism (e.g., corals); (g) Kang et al. 2011, ant‐fungal garden; (h) Hale et al. 2021, plant‐seed disperser