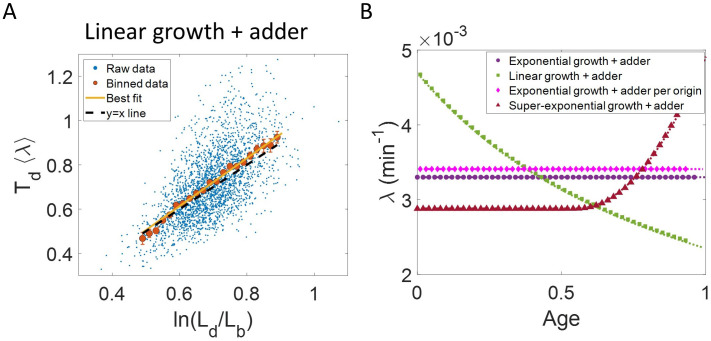
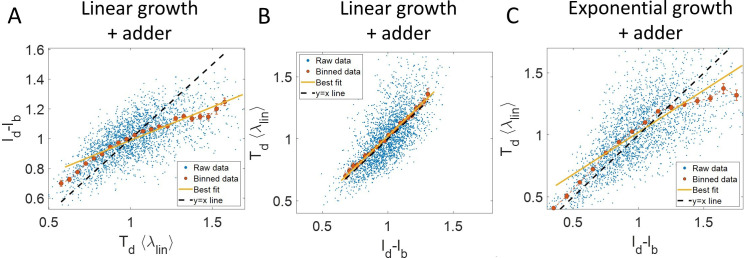
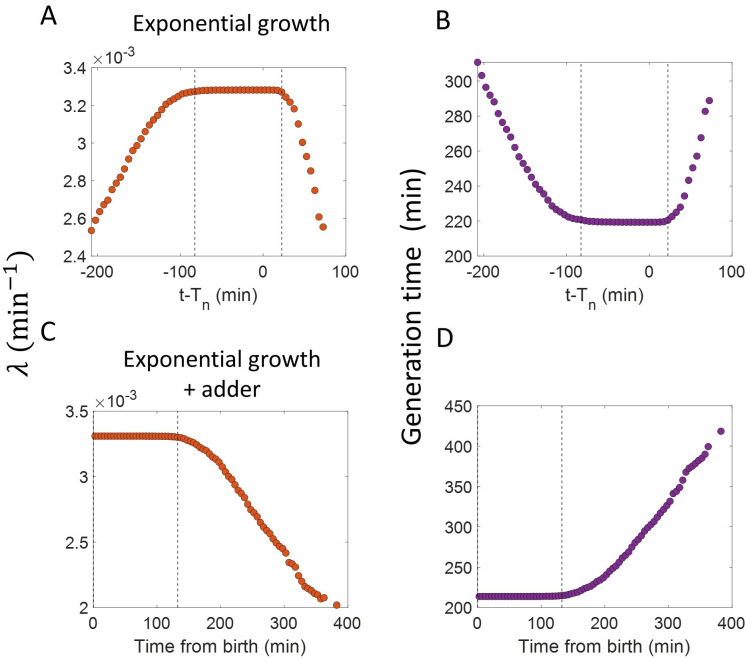
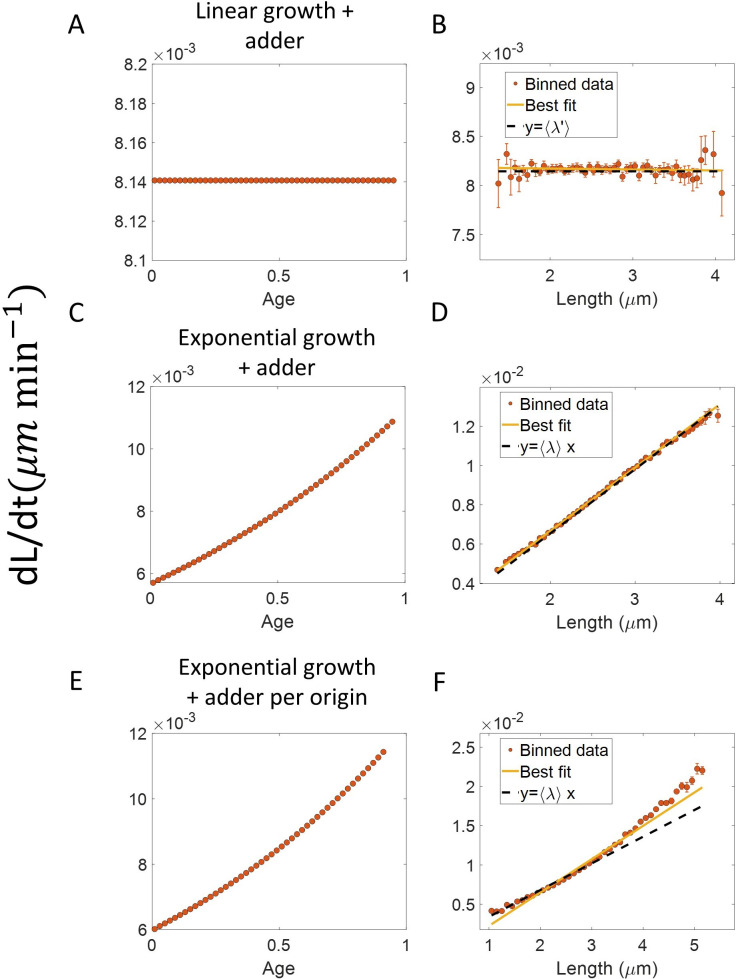
Figure 3. Differentiating linear growth from exponential growth.

(A) ${\displaystyle ⟨\lambda ⟩T_d}$ vs $\ln (\frac{L_d}{L_b})$ plot is shown for simulations of linearly growing cells following the adder model for N = 2500 cell cycles. The binned data (red) and the best linear fit on raw data (yellow) closely follows the y = x trend (black dashed line) which could be incorrectly interpreted as cells undergoing exponential growth. (B) The binned data trend for growth rate vs age plot is shown as purple circles for simulations of N = 2500 cell cycles of exponentially growing cells following the adder model. We observe the trend to be nearly constant as expected for exponential growth (purple dotted line). Since the growth rate is fixed at the beginning of each cell cycle in the above simulations, we do not show error bars for each bin within the cell cycle. Also shown as green squares is the growth rate vs age plot for simulations of N = 2500 cell cycles of linearly growing cells following the adder model. As expected for linear growth, the binned growth rate decreases with age as $\lambda \propto \frac{1}{1+age}$ (green dotted line). The binned growth rate trend (shown as magenta diamonds) is also found to be nearly constant as expected (shown as magenta dotted line) for the simulations of exponentially growing cells following the adder per origin model. We also show that the binned growth rate trend (red triangles) increases for simulations of the adder model with the cells undergoing faster than exponential growth. The trend is in agreement with the underlying growth rate function (shown as red dotted line) used in the simulations of super-exponential growth. Thus, the plot growth rate vs age provides a consistent method to identify the mode of growth. Parameters used in the above simulations of exponential, linear and super-exponential growth are derived from the experimental data in alanine medium. Details are provided in the Simulations section.

Figure 3—figure supplement 1. Predicting statistics based on a model of linear growth.

(A-B) Simulations of linearly growing cells following the adder model are carried out for N = 2500 cell cycles. (A) $l_d-l_b$ vs $⟨{\lambda }_{lin}⟩T_d$ plot is shown. The raw data is shown as blue dots. The binned data (in red) and the best linear fit on raw data (in yellow) deviate from the y = x line (black dashed line). Such a deviation can be predicted based on a model as discussed in detail in the Linear growth section. (B) $⟨{\lambda }_{lin}⟩T_d$ vs $l_d-l_b$ plot is shown. The binned data (in red) and the best linear fit on raw data (in yellow) agree with the y = x line (in black). (C) Simulations of exponentially growing cells following the adder model are carried out for N = 2500 cell cycles. $⟨{\lambda }_{lin}⟩T_d$ vs $l_d-l_b$ plot is shown. The binned data (in red) and the best linear fit on raw data (in yellow) deviate from the y = x line (in black) as expected for exponential growth. Parameters used in the simulations above are provided in the Simulations section.

Figure 3—figure supplement 2. Inspection bias in the growth rate vs time plots obtained from simulations.

(A) The binned growth rate trend as a function of time from the onset of constriction (t- $T_n$) is shown in red. Time t- $T_n=$ 0 corresponds to onset of constriction. The plot is shown for simulations of exponentially growing cells carried out over N = 2500 cell cycles. Constriction length is determined by a constant length addition from birth and division occurs after a constant length addition from constriction. (B) The average generation time for the cells present in each bin of (A) is shown. (C) For simulations of exponentially growing cells following the adder model (N = 2500), the binned growth rate (in red) vs time from birth plot is shown. (D) The average generation time for the cells present in each bin of (C) is shown. The vertical dashed lines show the time range in which the generation times are approximately constant and hence, the effects of inspection bias are negligible. Within that time range, the growth rate trend is found to be constant, consistent with the assumption of exponential growth.

Figure 3—figure supplement 3. Differential methods of quantifying growth.

(A-B) Simulations of linearly growing cells following the adder model are carried out for N = 2500 cell cycles. Cell size ($L$) data is recorded as a function of time within the cell cycle. (A) The red dots show the binned data for elongation speed as a function of age. The trend is almost constant in agreement with the linear growth assumption. (B) Elongation speed is also constant with cell size as expected for linear growth. The intercept value of the best linear fit on raw data (in yellow) provides the average elongation speed. (C-D) Simulations of exponentially growing cells following the adder model are carried out for N = 2500 cell cycles. (C) Elongation speed trend (in red) increases with age in agreement with the exponential growth assumption. (D) Elongation speed trend (in red) increases linearly with size. The slope of the best linear fit on raw data (in yellow) is equal to the average growth rate. (E-F) Simulations of exponentially growing cells following the adder per origin model are carried out for N = 2500 cell cycles. (E) Again, the elongation speed trend (in red) increases with age in agreement with the exponential growth assumption. (F) Elongation speed trend (in red) and the best linear fit on raw data (in yellow) deviates from the expected linear trend (black dashed line). This could be misinterpreted as non-exponential growth. Thus, we find that the binned data trend for the plot elongation speed vs size is model-dependent.