An uncertainty-aware, shareable, and transparent neural network architecture for brain-age modeling

A network-based quantification of brain aging uncovers and fixes a fundamental problem of all previous approaches.

Abstract

The deviation between chronological age and age predicted from neuroimaging data has been identified as a sensitive risk marker of cross-disorder brain changes, growing into a cornerstone of biological age research. However, machine learning models underlying the field do not consider uncertainty, thereby confounding results with training data density and variability. Also, existing models are commonly based on homogeneous training sets, often not independently validated, and cannot be shared because of data protection issues. Here, we introduce an uncertainty-aware, shareable, and transparent Monte Carlo dropout composite quantile regression (MCCQR) Neural Network trained on N = 10,691 datasets from the German National Cohort. The MCCQR model provides robust, distribution-free uncertainty quantification in high-dimensional neuroimaging data, achieving lower error rates compared with existing models. In two examples, we demonstrate that it prevents spurious associations and increases power to detect deviant brain aging. We make the pretrained model and code publicly available.

INTRODUCTION

Although aging is ubiquitous, the rate at which age-associated biological changes in the brain occur differs substantially between individuals. Building on this, the so-called “brain-age paradigm” (1) aims to estimate a brain’s “biological age” (2) and posits that brain age may serve as a cumulative marker of disease risk, functional capacity, and residual life span (3). In a typical brain-age study, a machine learning model is trained on neuroimaging data—usually whole-brain structural T₁-weighted magnetic resonance imaging (MRI) data—to predict chronological age. This trained model is then used to evaluate neuroimaging data from previously unseen individuals and evaluated on the basis of the “brain-age gap” (BAG) as defined by the difference between predicted and chronological age.

A decade after its inception, this approach has developed into a major component of biological age research with a plethora of publications linking individual differences between chronological and brain age to genetic, environmental, and demographic characteristics in health and disease [for a comprehensive review, see (4)]. For example, a higher brain age compared to chronological age has been associated with markers of physiological aging (e.g., grip strength, lung function, walking speed), cognitive aging (5), life risk (6), and poor future health outcomes including progression from mild cognitive impairment to dementia (7, 8), mortality (5), and a range of neurological diseases and psychiatric disorders [reviewed in (9)].

However, despite its scientific relevance and popularity, brain-age research faces numerous challenges, which hamper further progress and the translation of findings into clinical practice. First, the quantity and quality of the neuroimaging data upon which the underlying brain-age models are trained differ widely across studies, with only more recent studies training on more than 100 samples. Given the large number of voxels measured by modern structural MRI and the complexity of the multivariate machine learning models used in brain-age modeling, these small training sample sizes may lead to low-performance models with comparatively large errors. While studies drawing on larger training samples exist, historical models are of limited value as they cover only a certain age range [cf., for example, the UK Biobank (3) dataset including subjects older than 45 years only]. In contrast, more recent studies train on several publicly available datasets that have reached training sample sizes of up to N = 2001 covering the full adult age range (10). Also, more recent studies [enhancing neuro imaging genetics through meta-analysis (ENIGMA) (11) or Kaufmann et al. (12)] have reached very good performance in large training and validation datasets despite focusing on a limited set of morphological features. These studies clearly provide major improvements with regard to previous studies.

Second, the assessment of the performance of the trained model is often severely hampered by small validation datasets. With so-called leave-one-out cross validation—a validation scheme that relies on averaging performance across N models using a validation dataset size of N = 1 in each iteration—the norm rather than the exception, performance estimates are often highly variable. If independent model validation on previously unseen datasets is conducted at all, validation samples are often small. Since validation sample sizes below N = 100 may yield a substantial percentage of spuriously inflated performance estimates, the stability of brain-age estimates underlying many brain-age studies might be questioned (13). Further, validation on large independent datasets including data from multiple recruitment centers and imaging sites has only improved recently with studies such as Bashyam et al. (14), who used a cross-disorder sample comprising N = 11,729 participants. Also, brain-age models are regularly not evaluated regarding potential biases such as gender, for which fitting separate models might be beneficial.

Third, although the initial brain-age framework suggested linear relevance vector regression (RVR), algorithms commonly used today also include (nonlinear) support vector machines (SVMs) and, more recently, Gaussian process regressors (4). Often, the choice of algorithm is not justified, and empirical comparisons of different approaches are rare. Especially problematic is the fact that Gaussian process regression (GPR) and RVR runtimes scale cubically with the number of samples, rendering training on large datasets difficult. Also, models trained using these algorithms cannot be shared among researchers because of data protection issues as they allow for a partial or even complete reconstruction of the training data, thereby hampering external validation. Moreover, the lack of publicly available brain-age models forces researchers to use a large portion of their data for brain-age model training and validation—either vastly decreasing statistical power for subsequent analyses or introducing additional variation because of cross-validation.

Fourth, an analysis regarding which characteristics of the brain drive brain-age predictions is either not conducted at all, or results are not comparable across studies because of different preprocessing and algorithm-specific importance score mapping. For example, mapping SVM weights as a proxy for feature importance may yield vastly different results, compared with deriving Gaussian process g-maps (15), rendering results incomparable. In addition, studies investigate the properties and performance of the machine learning model, not the interaction with single-subject data underlying predictions, thereby disregarding individual differences driving predictions. With ever-growing samples allowing for the application of ever more sophisticated machine learning algorithms, this underscores the need for a principled approach to transparency [cf. explainability (16)] that is comparable across algorithms.

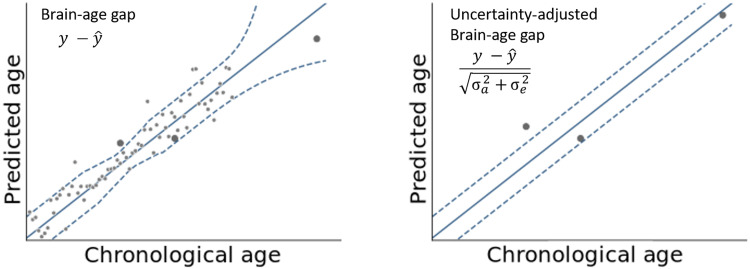
The core metric of the field—i.e., the difference between chronological and predicted brain age (commonly referred to as BAG)—does not account for uncertainty in model predictions. Not adjusting the BAG for uncertainty, however, renders findings of altered aging confounded with data density and variability [cf. the concept of normative modeling (17) for an introduction]. Specifically, deviations between chronological age and BAG may arise not only from neural changes as intended but also erroneously from high uncertainty. Therefore, failing to properly model uncertainty may lead to spurious results, which depend on the characteristics of the training sample and properties of the model rather than on the underlying association of a variable with BAG. Uncertainty arising from noise inherent in the observations (i.e., aleatory uncertainty) and uncertainty arising from the model itself (i.e., epistemic uncertainty) must be considered. Figure 1 illustrates the concept of adjusting the BAG by individual uncertainty.

Fig. 1. Example data illustrating the effects of adjusting the BAG for individual uncertainty.

Left: Regression model (solid line) with uncertainty estimate (e.g., 95% predictive interval; dotted lines) trained on toy data with varying density and variability (light grey) was applied to three test samples (dark gray). BAG is defined as a test sample’s distance from the regression line. Right: Uncertainty adjustment increases BAG in areas of low uncertainty (left-most test sample) and decreases it in areas of high uncertainty (right-most test sample). σ_a, aleatory uncertainty; σ_e, epistemic uncertainty.

While not commonly used in brain-age research, algorithms often used in brain-age modeling such as RVR and the GPR are, in principle, capable of modeling aleatory and epistemic uncertainty. For high-dimensional inputs, however, uncertainty estimation becomes exceedingly difficult using these methods. This has sparked a plethora of research into alternative approaches, especially for neural networks (18–20). While interesting, most of these approaches do not consider aleatory and epistemic uncertainty together, and none have been applied to brain-age research.

Here, we address these issues by (i) introducing a robust Monte Carlo dropout composite quantile regression (MCCQR) Neural Network architecture capable of estimating aleatory and epistemic uncertainty in high-dimensional data; (ii) training our model on anatomical MRI data of N = 10,691 individuals between 20 and 72 years of age from the German National Cohort (GNC); (iii) validating the resulting model using leave-site-out cross-validation across 10 recruitment centers and 3 additionally independent, external validation sets comprising a total of N = 4004 samples between 18 and 86 years of age; (iv) benchmarking the MCCQR model against the five most commonly used algorithms in brain-age modeling with regard to predictive performance and quantification of uncertainty; (v) systematically assessing model bias for gender, age, and ethnicity; and (vi) developing a unified explainability approach based on the combination of occlusion-sensitivity mapping and generalized linear multilevel modeling to identify brain regions driving brain-age predictions. Building on data from the GNC study, we apply the MCCQR model to predict uncertainty-adjusted brain-age gaps and investigate their association with body mass index (BMI) and major depressive disorder. As training data cannot be reconstructed from the MCCQR model, we make the pretrained model publicly available for validation and use in future research.

RESULTS

Model performance

We evaluated our MCCQR Neural Network model against five commonly used algorithms in brain-age modeling—namely, the RVR, linear SVM, SVM with a radial basis function kernel (SVM-rbf), GPR, and least absolute shrinkage and selection operator (LASSO) regression—regarding predictive performance. For comparison, we also evaluated a version of our neural network model without uncertainty quantification but with an otherwise identical network structure and hyperparameters [artificial neural network (ANN)].

We iteratively trained our model on data of patients recruited by 9 of the 10 recruitment centers contributing MRI data to the GNC (N = 10,691) and predicted brain age for all samples from the remaining center. This leave-site-out cross-validation showed a median absolute error (MAE) across all 10 recruitment centers of 2.94 years (SD = 0.22) for the MCCQR model. Performance of the other algorithms ranged from 3.05 (SD = 0.22) for both GPR and SVM to 4.25 (SD = 0.30) for LASSO regression. Results of 10-fold cross-validation corroborate this ranking of performance with the MCCQR, reaching an MAE of 2.95 years (SD = 0.16) with GPR and SVM MAE = 3.09 (SD = 0.11) and LASSO regression MAE = 4.19 (SD = 0.11). The ANN obtained MAE = 3.10 (SD = 0.14) for leave-site-out cross-validation and MAE = 3.02 (SD = 0.15) for 10-fold cross-validation.

While cross-validation performance—particularly across recruitment centers—usually provides good estimates of generalization performance, it does not consider additional sources of variability such as different data acquisition protocols, alterations in recruitment, or sample characteristics. Therefore, we validated all models in three independent samples (N = 4004), namely, the BiDirect study, the Marburg-Münster Affective Disorders Cohort Study (MACS), and the Information eXtraction from Images (IXI) dataset. To assess stability under real-world conditions of later use, these samples covered a larger age range than the training data (20 to 86 years versus 20 to 72 years in the GNC sample) as well as less restrictive exclusion criteria (for a detailed description, see Materials and Methods): For the BiDirect sample (N = 1460), the MCCQR model reached an MAE of 3.45 years. Performance of the other models ranged from 3.60 for the RVR to 4.79 for the SVM-rbf. The ANN reached an MAE of 3.76 years. In the MACS sample (N = 1986) (21), the MCCQR model reached an MAE of 3.92, while the other models obtained generalization performance between 4.15 (GPR and SVM) and 9.92 (SVM-rbf). The ANN reached MAE = 3.76 years. Last, we evaluated performance on the publicly available IXI dataset (www.brain-development.org, N = 561). The MCCQR model and the ANN reached an MAE of 4.57 and 4.48 years, respectively. The other models’ performances ranged between MAE = 4.91 years (RVR) and MAE = 8.10 (SVM-rbf). Table 1 shows individual model performance for leave-site-out, 10-fold cross-validation, and the three independent validation samples. The MCCQR achieves lower MAE compared with all other algorithms commonly used in brain-age research. The ANN displays lower MAE than the MCCQR in two of five cases, indicating a slight advantage for the neural network architecture disregarding uncertainty in these cases.

Table 1. MAE for all models, cross-validation schemes, and independent validation samples.

CV, cross-validation. For cross-validation, SD across folds is given in parentheses.

Model	Leave-site- out CV	10-Fold CV	BiDirect	MACS	IXI
RVR	3.37 (0.16)	3.32 (0.13)	3.60	5.07	4.91
GPR	3.05 (0.22)	3.09 (0.11)	3.74	4.15	5.03
SVM	3.05 (0.22)	3.09 (0.11)	3.74	4.15	5.03
SVM-rbf	4.19 (0.27)	4.16 (0.16)	4.79	9.92	8.10
LASSO	4.25 (0.30)	4.19 (0.12)	4.44	8.35	6.94
ANN	3.10 (0.14)	3.02 (0.15)	3.56	3.76	4.48
MCCQR	2.94 (0.22)	2.95 (0.16)	3.45	3.91	4.57

Uncertainty quantification

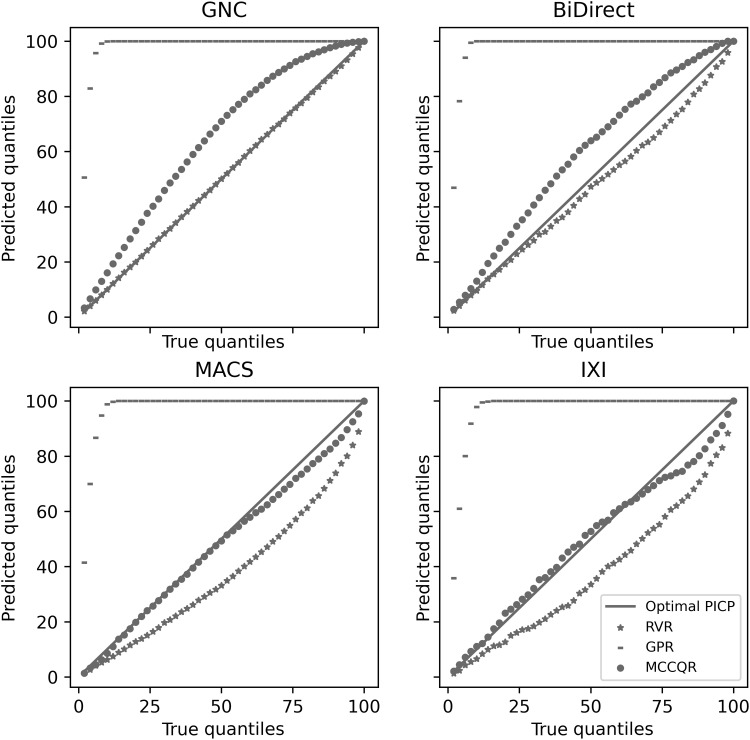
Adjusting BAG for aleatory and epistemic uncertainty is crucial as findings of altered aging may otherwise be driven by, e.g., training data density and variability. While algorithms such as RVR and GPR are, in principle, capable of modeling aleatory and epistemic uncertainty, performance on high-dimensional data may be problematic. To evaluate the quality of the uncertainty quantification, we estimated uncertainty using the MCCQR, RVR, and GPR (note that the other algorithms do not readily provide uncertainty estimates). Then, we assessed prediction interval coverage probability (PICP), i.e., the probability that a sample’s true value is contained within the predictive interval. Figure 2 depicts PICPs for given quantile values for cross-validation and the three independent validation datasets. Note that underestimation of uncertainty is highly problematic as samples may be erroneously characterized as deviants from the normal brain-aging trajectory. Overestimation of uncertainty decreases the ability to detect outliers, rendering the approach more conservative. While the GPR substantially overestimates uncertainty in all datasets, RVR and MCCQR provide high-quality uncertainty estimations for GNC and BiDirect datasets. MCCQR outperforms RVR in the MACS and IXI datasets. Note that incorporating epistemic or aleatory uncertainty alone—as has recently been suggested (20) for brain-age models—systematically underestimates uncertainty (see fig. S1).

Fig. 2. PICP for leave-site-out GNC and independent validation samples (BiDirect, MACS, and IXI) for the RVR, the GPR, and our MCCQR Neural Network.

Underestimation (overestimation) of uncertainty occurs if empirical PICPs are below (above) optimal PICP as indicated by the solid line.

Relevance of uncertainty adjustment

As outlined above, brain-age gaps may arise not only from brain changes as intended but also erroneously from high uncertainty, i.e., a person may have a large BAG not only due to actual changes in the brain but also due to properties of the underlying machine learning model that arise from characteristics of the training data such as data density and variability. Here, we empirically demonstrate two such cases.

First, we investigated the association of BAG and BMI in the GNC study data. On the basis of this, we find a significant association between BMI and BAG (F_1,10,344 = 7.06, P = 0.008). However, this effect is no longer observed if uncertainty is considered by scaling BAG with the SD of the individual predictive distribution (F_1,10,344 = 0.15, P = 0.697). Correspondingly, effect size (partial η²) was reduced by 98%.

Second, we investigated the difference in BAG between a population sample (N = 1612) and patients suffering from major depressive disorder (N = 1541) from the MACS and the BiDirect sample. While the standard analysis based on BAG failed to reveal a significant difference (F_1,3148 = 1.61, P = 0.204), the same analysis based on uncertainty-corrected BAG detected a significant effect (F_1,3148 = 5.59, P = 0.018). Likewise, partial η² was increased by 247%.

Bias assessment

As machine learning models are not programmed but trained, they will mimic systematic biases inherent in their training data (22). While this potential algorithmic bias must be carefully investigated with regard to performance differences in specific subgroups to determine for which populations it yields robust estimates, it is often neglected in brain-age research [for an in-depth discussion, see (23)]. Here, we investigated model performance differences for gender, ethnicity, and age.

We found that model performance of the MCCQR did not substantially differ with regard to gender, reaching a standardized MAE of 0.459 for females and a standardized MAE of 0.456 for males in the BiDirect dataset (due to different age ranges between males and females, we standardized MAE to make results comparable). In the MACS dataset, standardized MAE reached 0.298 in females and 0.264 in males. For the IXI dataset, the model reached a standardized MAE of 0.264 in females and 0.300 in males. Note that we defined gender as male and female as no further information on other genders was available. Regarding ethnicity, we tested our model on a publicly available dataset from Beijing Normal University (N = 179) between 18 and 28 years of age. Despite the low age range, the MCCQR failed to provide reasonable brain-age predictions with an MAE = 8.39. Last, we investigated model performance across different ages. As commonly reported in brain-age studies, we observed a correlation between BAG and age (r = −0.39) and between uncertainty-corrected BAG and age (r = −0.43) in the BiDirect sample. The same is true for the MACS dataset (BAG, r = −0.36; uncertainty-corrected BAG, r = −0.40) and the IXI dataset (BAG, r = −0.70; uncertainty-corrected BAG r = −0.75), implying that in all three validation datasets, performance is better in older participants (see fig. S2). Thus, we included age as a covariate in all statistical analyses involving the BAG in the “Relevance of uncertainty adjustment” section.

Explainability

Combining occlusion-sensitivity mapping and generalized linear multilevel modeling, we investigated which brain regions are relevant for accurate brain-age prediction in the MACS sample (N = 1986). We show that occlusion—i.e., the exclusion of data—of any of the 116 regions of the Automated Anatomical Labeling brain atlas significantly affected model performance (largest P < 0.001; see table S1). Occlusion of five regions leads to increased BAG, while occlusion of 107 regions decreased BAG. Strongest BAG-increasing effects were observed for left and right putamen and left Heschl’s gyrus. Strongest BAG-decreasing effects were observed for right inferior temporal gyrus, left middle temporal gyrus, and left middle frontal gyrus (see fig. S3).

DISCUSSION

We trained an uncertainty-aware, shareable, and transparent MCCQR Neural Network on N = 10,691 samples from the GNC. This model achieves lower error rates compared with existing models across 10 recruitment centers and in three additional, independent validation samples (N = 4004). The model thus generalized well to independent datasets with larger age range than the training data. In contrast to currently used algorithms—which either do not provide uncertainty estimates or over- or underestimate uncertainty—the MCCQR model provides robust, distribution-free uncertainty quantification in high-dimensional neuroimaging data. Building on this, we show in N = 10,691 subjects from the GNC that a spuriously inflated brain-age deviation effect for BMI is found if uncertainty is ignored. Likewise, we demonstrate in the BiDirect sample that correcting for uncertainty also increases power to detect altered aging in major depressive disorder (N = 688) as compared with a population sample (N = 719). These findings underscore the need to adjust brain-age gaps for aleatory and epistemic uncertainty. Nonadjustment for these uncertainty components led to false-positive and false-negative findings in our studies.

While the importance of uncertainty quantification has been discussed at length in the context of normative modeling [cf. (17) for a discussion of the relevance of including aleatory and epistemic uncertainty] and two of the algorithms commonly used in brain-age research (mainly GPR) provide uncertainty quantification, it has largely been ignored in the brain-age literature to date. This could be due to several reasons: First, GPR and RVR do not scale well to large datasets as they require the inversion of the kernel matrix, and more scalable GPRs based on variational Bayes are still an active area of research. Second, reasonable uncertainty estimation for GPR models becomes exceedingly difficult in situations in which the number of features far exceeds the number of samples as is the case in virtually all MRI studies. This issue also arose in our study, leading to unreasonable uncertainty estimates (cf. Fig. 2). Third, GPR and RVR models require the full training sample to make predictions. While scalable GPR approaches only require a subset of the training data, the quality of predictions directly depends on the number and representativity of these so-called induction points. Note that in our study, the RVR algorithm’s uncertainty quantification was of high quality in the GNC and BiDirect data but decreased in comparison to the MCCQR in the MACS and IXI datasets. This performance might render it a viable alternative with regard to uncertainty quantification in some cases. However, as literally the entire training dataset is required to make predictions using RVR, the data protection issues arising from this largely prohibit model sharing and thus independent validation.

A recent study also recognized the issue of uncertainty quantification for brain-age modeling and used quantile regression (QR) to estimate aleatory uncertainty in brain-age prediction (20). While this approach accounts for aleatory uncertainty induced by, e.g., measurement error, it does not consider epistemic uncertainty, i.e., uncertainty in the model weights. Empirically, we showed that accounting for aleatory uncertainty only substantially underestimated true uncertainty (cf. fig. S1). If data density differs over age groups, seemingly uncertainty-corrected brain-age gaps may still be confounded. Thereby, deviant brain ages might spuriously arise from differential training data density—an effect especially problematic given the relatively small training sample sizes used in most brain-age studies. In addition, it may be difficult to detect as only subsets of BAGs of a given sample are affected.

As mentioned above, our approach is intimately related to normative modeling (17). In contrast to this approach, however, we do not seek to quantify voxel-wise deviation, but deviation on the level of the individual. Hence, we do not predict single voxel data from chronological age, but chronological age from the multivariate pattern of whole-brain data. While this directly yields brain-age predictions on the level of the individual—hence circumventing the need to estimate individual-level predictions based on extreme value statistics or the combination of deviations across voxels as has been suggested for normative modeling—it cannot directly be used as a brain mapping method. To this end, we adopted an occlusion-sensitivity mapping approach, which quantifies regional importance as the reduction in BAG when features from a specific region are withheld (24). Compared with other approaches to explainability such as the visualization of the network weights using, e.g., layer-wise relevance propagation (25), occlusion-sensitivity mapping comes with the benefit of yielding relevant features for each individual. From a methodological point of view, the multilevel model used in this study holds crucial advantages over the commonly used mass-univariate approach. First, in the mass-univariate approach, estimates for the effect of the predictors on BAG are only informed by one region. In the multilevel framework, however, each estimate is informed not only by its region but also by all other regions. Second, the multilevel model enables us to include theoretically necessary control variables, which vary over brain regions, but not over samples, such as the size of each region of interest (ROI). Third, the multilevel approach controls for dependency within the model, alleviating the need for multiple comparison correction as required in the mass-univariate case (26). This analysis revealed that occlusion of any region resulted in a significant change of brain-age predictions, underscoring the multivariate, distributed nature of aging in the brain. Also, our results mitigate concerns that high-performance brain-age models might focus on a small subset of features not affected by pathology (14).

Machine learning models are trained on data and may thus mimic systematic biases inherent in their training data. Investigating performance in specific subgroups revealed that the MCCQR performed comparably for females and males. As is the case for most brain-age models, we observed a correlation between BAG and age. This behavior is not unexpected, as errors in regression modeling will always tend toward the mean (age in this case) of the training set. Nonetheless, it requires modeling age as a covariate in all analyses aiming to associate BAG with variables of interest [for an introduction to age-bias correction approaches in brain-age modeling, see (27)]. Investigating ethnicity bias, we showed that our model fails to accurately predict age in a Chinese sample. On the one hand, this limitation was to be expected given the GNC aims to recruit a random population sample of Germany. One the other hand, this effect underscores the need for systematic bias assessment. The MCCQR also offers an opportunity to remedy this issue (see below).

The MCCQR—in contrast to most approaches used in brain-age research—does not allow for the reconstruction of individual samples from the training sample. Thus, we make it publicly available. This is beneficial for three reasons: First, it allows others to independently assess MCCQR model performance. Second, it may markedly increase power and robustness of smaller brain-age studies by circumventing the need to train a brain-age model and test associations with variables of interest in the same dataset. Third, it enables researchers to continue training the model with more data. For example, fine-tuning the MCCQR model with data from other ethnic groups—e.g., Asian—would help the model generalize better. In this regard, future studies using additional data from ethnic groups ought to clarify whether it is ethnicity per se or, e.g., different MRI scanning protocols that have led to lower performance. In the same vein, our model could be extended by adding, e.g., three-dimensional convolution layers [as done, e.g., in (10, 14)] to the MCCQR to allow predictions directly from raw MRI data without the need for preprocessing. While this study constitutes a first step toward incorporating uncertainty in brain-age modeling, it is limited in several ways. First, we evaluated the model neither on a large sample of older participants (>72 years) nor on a sample of adolescents. Second, we did not explicitly model GNC imaging sites during training, and a benchmark against state-of-the-art deep learning approaches is missing. Future studies could therefore not only evaluate the model but also increase generalization and usability by training on more diverse datasets and developing model architecture. We facilitate this research by making the pretrained model publicly available with this publication.

In light of this, we provide the uncertainty-aware, shareable, and transparent MCCQR architecture and pretrained model with the intention to stimulate further research and increase power for small-sample analyses. The pretrained PHOTON-AI model and code can be downloaded from the PHOTON AI model repository (www.photon-ai.com/repo).

MATERIALS AND METHODS

Training and validation samples

Whole-brain MRI data from five sources were used. We trained the MCCQR on the GNC sample. Results for leave-site-out and 10-fold cross-validation are also based on the GNC sample. Independent validation was based on the BiDirect sample, the MACS data, and the IXI dataset. Ethnicity bias assessment was conducted using the Beijing Normal University dataset (see below). In the following, we describe each dataset in more detail. Also, table S2 provides further sample characteristics, including sample sizes, gender distribution, age minimum and maximum, and SD.

German National Cohort

This cohort is one of the population-based “megacohorts” and examines 205,000 Germans, aged 20 to 72 years, in 18 study centers across Germany between 2014 and 2019 using a comprehensive program. Specifically, this included a 3.0-Tesla whole-body MRI (T₁w-MPRAGE) in 30,000 participants, performed in five GNC imaging centers equipped with dedicated identical magnets (Skyra, Siemens Healthineers, Erlangen, Germany) examining participants from 11 of the centers. This analysis is based on the “data freeze 100K” milestone for the first 100,000 participants, which also included the first 10,691 participants with completed MRIs of sufficient quality [for a detailed protocol, see (28, 29)]. We calculated BMI from directly measured height and weight (kg/m²; mean Becks Depression Inventory (BDI) = 26.82; SD BDI = 4.76). To ensure that our models were not driven by data quality or total intracranial volume (TIV), we assessed the predictive power of the three data quality parameters provided by the Cat12 toolbox and TIV. We show that TIV, bias, noise, and weighted average interquartile range combined explain only 9.06% of variation in age using a linear SVM with 10-fold cross-validation compared to the 86% achieved by the MCCQR model.

BiDirect

The BiDirect study is an ongoing study that comprises three distinct cohorts: patients hospitalized for an acute episode of major depression, patients 2 to 4 months after an acute cardiac event, and healthy controls randomly drawn from the population register of the city of Münster, Germany. Baseline examination of all participants included a structural MRI of the brain, a computer-assisted face-to-face interview about sociodemographic characteristics, a medical history, an extensive psychiatric assessment, and collection of blood samples. Inclusion criteria for the present study were availability of completed baseline MRI data with sufficient MRI quality. All patients with major depressive disorder had an episode of major depression at the time of recruitment and were either currently hospitalized (>90%) or had been hospitalized for depression at least once during the 12 months before inclusion in the study (<10%). Further details on the rationale, design, and recruitment procedures of the BiDirect study have been described elsewhere (30).

Marburg-Münster Affective Disorder Cohort Study

Participants were recruited through psychiatric hospitals or newspaper advertisements. Inclusion criteria included mild, moderate, or partially remitted major depressive disorder episodes in addition to severe depression. Patients could be undergoing inpatient, outpatient, or no current treatment. The MACS was conducted at two imaging sites: University of Münster, Germany, and University of Marburg, Germany. Further details about the structure of the MACS (31) and MRI quality assurance protocol (21) are provided elsewhere. Inclusion criteria for the present study were availability of completed baseline MRI data with sufficient MRI quality [see (21) for details].

Information eXtraction from Images

This dataset comprises images from normal, healthy participants, along with demographic characteristics, collected as part of the IXI project available for download (https://brain-development.org/ixi-dataset/). The data have been collected at three hospitals in London (Hammersmith Hospital using a Philips 3T system, Guy’s Hospital using a Philips 1.5T system, and Institute of Psychiatry using a GE 1.5T system). Inclusion criteria for the present study were availability of completed baseline MRI data.

Beijing Normal University

This dataset includes 180 healthy controls from a community (student) sample at Beijing Normal University in China. Inclusion criteria for the present study were availability of completed baseline MRI data. Further details can be found online (http://fcon_1000.projects.nitrc.org/indi/retro/BeijingEnhanced.html).

MRI preprocessing

MRI data were preprocessed using the CAT12 toolbox (built 1450 with SPM12 version 7487 and Matlab 2019a; http://dbm.neuro.uni-jena.de/cat) with default parameters. Images were bias corrected, segmented using tissue classification, normalized to MNI-space using DARTEL normalization, smoothed with an isotropic Gaussian Kernel (8 mm FWHM), and resampled to 3-mm isomorphic voxels. Using the PHOTON AI software (see “Model training and validation” section below), a whole-brain mask comprising all gray matter voxels was applied, data were vectorized, features with zero variance in the GNC dataset were removed, and the scikit-learn Standard Scaler was applied.

MCCQR model

Commonly, regression models f^W(x) are used to describe the relationship of features X = (x,…,x_n) and a target variable y = (y₁,…,y_n). We denote model predictions $\widehat{y}=f^W(x)$ with W the model parameters. Commonly, these regression models provide predictions as point estimates rather predictive distributions. We thus consider two types of uncertainty in accordance with Kendall and Gal (32). The first—aleatory uncertainty—captures noise inherent in the observations. The second—epistemic uncertainty—accounts for uncertainty in the model. While the former is irreducible for a given model, the latter depends on data availability and training and is thus affected by data density and can be reduced by training (i) the model based on the loss function and (ii) with additional data. While numerous approaches to uncertainty quantification have been suggested, no commonly accepted approach exists. While Bayesian approaches such as GPR provide a mathematically elegant framework, such approaches often fail in high-dimensional settings or are not scalable to large datasets (33). In particular, capturing aleatory and epistemic uncertainty within the same neural network model remains challenging (34). Here, we suggest to combine composite QR and Monte Carlo dropout to model aleatory and epistemic uncertainty within a single framework, respectively.

Composite QR

QR provides an estimate not only of the conditional mean (as is done when optimizing for mean absolute error) but also of any quantile in the data. This comes with two advantages. First, we can estimate the median (instead of the mean), thereby obtaining a prediction more robust to potential outliers. Second, predicting quantiles can yield predictive intervals, thereby modeling aleatory uncertainty. For example, we cannot only predict a sample’s target value but also the 95% confidence bounds of this prediction. This makes QR interesting whenever percentile curves are of interest, e.g., when screening for abnormal growth.

Commonly, conditional quantiles for predetermined quantile probabilities are estimated separately by different regression equations. These are then combined to build a piecewise estimate of the conditional response distribution. As this approach is prone to “quantile crossing,” i.e., QR predictions do not increase with the specified quantile probability τ, composite QR was introduced (35). In composite QR, simultaneous estimates for multiple values of τ are obtained, and the regression coefficients are shared across the different QR models. In essence, we aim to approximate a single τ-independent function that best describes the function to be learned. Structurally, composite QR differs from QR only in that the QR error (tilted loss) function is summed over many, usually equally spaced values of τ. Specifically, QR is implemented using the QR error function (36) to optimize a neural network via

$$E_{\mathrm{\tau }}=\frac{1}{N}{\displaystyle \sum _{t=1}^N}{\mathrm{\rho }}_{\mathrm{\tau }}(y(t)-\widehat{y}(t))$$

with the tilted loss function ρ

$${\mathrm{\rho }}_{\mathrm{\tau }}(\mathrm{\epsilon })=\mathrm{\tau }·\mathrm{\epsilon } \text{if} \mathrm{\epsilon }\ge 0,\text{else} (1-\mathrm{\tau })\mathrm{\epsilon }$$

Composite QR extends this idea to estimating multiple quantiles simultaneously. This is not only more stable but also computationally more efficient as fewer coefficients and fewer operations during weight updating are required. To achieve this, we modified the QR error function (above) to

$$E_{C\mathrm{\tau }}=\frac{1}{\mathrm{KN}}{\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{t=1}^N}{\mathrm{\rho }}_{{\mathrm{\tau }}_k}(y(t)-{\widehat{y}}_{{\mathrm{\tau }}_k}(t))$$

where τ_k are usually equally spaced, for example, ${\mathrm{\tau }}_k=\frac{k}{K+1}$ for k = 1,2,…, K as suggested by Cannon (18). Specifically, we calculate 101 equally spaced quantile values for 0 < τ < 1. To allow for continuous sampling during prediction, we linearly interpolated these quantile values. Note that while this approach does not formally guarantee the absence of quantile crossover, composite QR reduced the likelihood so much that we never empirically observed quantile crossover for any of the more than 1.48 billion quantiles (arising from 101 quantiles, 14,695 samples, and 1000 draws from the predictive distribution per sample) estimated during independent and cross-validation in this study.

Monte Carlo dropout

While composite QR captures aleatory uncertainty, it does not account for epistemic uncertainty, i.e., uncertainty in the model parameters. For example, epistemic uncertainty should be higher in regions of the input space where little data are available, whereas it should be lower in regions with high data density. While we could, in principle, model each weight of a neural network as distribution from which to sample weight values during prediction, estimating these probabilistic models remains challenging for high-dimensional data. Following Gal and Ghahramani (19), we therefore adopted a Monte Carlo dropout approach. While dropout is commonly used for regularization during neural network training, the Monte Carlo dropout approach enforces dropout during training and at test time. Thus, dropout can be used to obtain T predictions for the same input with different active neurons. This allows the estimation of p(y|f^W(x)), the mean probability of a prediction given a test input X = (X₁,…,X_n) for the neural network f with the according weights W. We therefore define our likelihood as a Gaussian with mean given by the model output according to Gal and Ghahramani (19)

$$p(y\mid f^W(x))=N(f^W(x),{\mathrm{\sigma }}^2)$$

We can then calculate the mean probability using Monte Carlo dropout performing T forward passes using randomly sampled weight values W_i from the neural network using dropout as

$$p(y\mid f^W(x))=\frac{1}{T}{\displaystyle \sum _{i=1}^T}p(f^W(x)=k\mid x,W_i)$$

Monte Carlo dropout composite QR

To model epistemic and aleatory uncertainty simultaneously within the same framework, we combined Monte Carlo dropout and composite QR described above. Specifically, we implemented the resulting MCCQR Neural Network consisting of one hidden layer with 32 rectified linear units using Tensorflow 2.0 together with tensor flow probability for robust median MAE calculation over batches. Note that we used MAE instead of the more common mean absolute error as the median is more robust to outliers compared to the mean. We trained for 10 epochs with a learning rate of 0.01, a batch size of 64, and a dropout rate of 0.2 using the Adam Optimizer with default settings. Predictions were obtained by sampling 1000 times from each sample’s predictive distribution with random τ values and dropout enabled. A sample’s brain-age prediction was computed as the median of the resulting values. Likewise, uncertainty was computed as the SD of the resulting values.

Reconstruction of individual-level data

Machine learning models traditionally used in brain-age modeling allow for the reconstruction of individual-level data. For our model, however, only saving model parameters and network architecture is required. Reconstructing individual-level data from this information alone is not possible for quantitative and conceptual reasons: Considering the quantity of information, our final model contains 1,269,701 parameters, 64 of which are not trainable. The complete training dataset consists of 10,696 images containing 39,904 voxels each, resulting in 426,733,376 parameters in the dataset. This amounts to about 336 times the number of parameters in our model, rendering it incapable of “memorizing” the data. Considering the conceptual nature of the training process, our model applies the Monte Carlo dropout. This method—used to counter overfitting and to estimate epistemic uncertainty—randomly reduces the number of active units during a forward pass. As the network parameters are optimized for inference across the whole training set, the network is not capable of compressing the images. Thus, we cannot recover individual trainings samples from the network.

Benchmarking alternative machine learning models

We evaluated our MCCQR Neural Network model against five commonly used algorithms in brain-age modeling—namely, the RVR, linear SVM, SVM-rbf, GPR, and LASSO regression. We used the fast-rvm implementation from sklearn-bayes (https://github.com/AmazaspShumik/sklearn-bayes) and used SVM, GPR, and LASSO implementations from sci-kit learn (37) with default settings. For comparison, we also evaluated a version of our neural network model without uncertainty quantification but with an otherwise identical network structure and hyperparameters optimizing mean absolute error over predictions instead of the tilted loss function used for the MCCQR model.

Model training and validation

All models were trained and cross-validated using the PHOTON AI software (www.photon-ai.com) for leave-site-out and 10-fold cross-validation on the GNC sample. Independent validation was conducted using PHOTON AI’s .photon format for pipeline-based prediction with the BiDirect, MACS, IXI, and Beijing Normal University samples.

Generalized linear multilevel modeling for occlusion-sensitivity mapping

Occlusion-sensitivity mapping—in analogy to occlusion-based approaches for two-dimensional images (24)—quantifies regional importance as the reduction in performance when features from a specific region are withheld. Occlusion was implemented by sequentially setting all voxels within each of the 116 ROIs of the AAL brain atlas (38) to zero. Occlusion sensitivity is widely used to gain insight into which regions of an image a machine learning model uses for prediction. A region is considered more important if model performance decreases more strongly when information from this region is withheld.

To quantify this notion of importance, we combined occlusion-sensitivity mapping with generalized linear multilevel modeling. Specifically, we used multiple linear regression using the R packages lme4 to model the difference between BAG based on whole-brain data and BAG if information from a specific atlas region is withheld.

To investigate regionally specific effects, we computed uncertainty-corrected BAG estimates for each individual and ROI (i.e., 116 regions from the AAL atlas distributed with statistical parametric mapping (SPM); www.fil.ion.ucl.ac.uk/spm/) independently. Then, we predicted uncertainty-corrected BAG from a group factor with AAL regions as factor levels, controlling for chronological age, site (where appropriate), gender, and ROI size. The ROI group factor was defined as treatment contrast with the whole-brain (no occlusion) level as reference factor. This way, ROI effect estimates can easily be interpreted as difference in BAG from the full model. P values for ROI factor level effects were computed using the Kenward-Roger approximation (39) as implemented in the afex R package. This approach allows us to test whether the occlusion of a given region results in an above-chance change of predictive performance. While beyond the scope of this paper, the combination of occlusion-sensitivity mapping and generalized linear multilevel modeling also allows for the investigation of regional effects between clinical groups.

More generally, our approach can be considered a form of model-independent explainable AI: In recent years, a large number of methods have been proposed that aim to shed light on the contribution of variables or groups of variables on a model prediction [for a review and best practice, see (40)]. Among those are algorithm-specific approaches such as layer-wise relevance propagation that work with deep neural networks or the weight mapping for SVMs. In essence, these techniques provide (qualitative) heatmaps, i.e., help to understand the informational flow in the network. In contrast, more general approaches ask how the prediction for a single sample/participant would change if the data changed (e.g., if we did not have variable x or if its single-to-noise ratio changes). As we aimed to quantify the effect of omitting/occluding ROIs independent of a specific training sample, we opted for occlusion mapping here.

Supplementary Materials

This PDF file includes:

Supplementary Text

Figs. S1 to S3

Tables S1 and S2

View/request a protocol for this paper from Bio-protocol.