Abstract
One key feature of proteins that form liquid droplets by phase separation inside a cell is multivalency—the presence of multiple sites that mediate interactions with other proteins. We know little about the variation of multivalency on evolutionary time scales. Here, we investigated the long-term evolution (∼600 million years) of multivalency in fungal mRNA decapping subunit 2 protein (Dcp2), and in the FET (FUS, EWS and TAF15) protein family. We found that multivalency varies substantially among the orthologs of these proteins. However, evolution has maintained the length scale at which sequence motifs that enable protein–protein interactions occur. That is, the total number of such motifs per hundred amino acids is higher and less variable than expected by neutral evolution. To help explain this evolutionary conservation, we developed a conformation classifier using machine-learning algorithms. This classifier demonstrates that disordered segments in Dcp2 and FET proteins tend to adopt compact conformations, which is necessary for phase separation. Thus, the evolutionary conservation we detected may help proteins preserve the ability to undergo phase separation. Altogether, our study reveals that the length scale of multivalent interactions is an evolutionarily conserved feature of two classes of phase-separating proteins in fungi and vertebrates.
Keywords: phase separation, evolution, multivalency, RNA binding, FUS, P-body
Introduction
Proteins that undergo liquid–liquid phase separation in a cell have various features that facilitate their condensation into liquid droplets. The presence of multiple interaction sites (multivalency) is one of these features. (Li et al. 2012; Brangwynne et al. 2015; Banani et al. 2017). Despite the pivotal role of multivalency, we know little about its evolution. The reason is that multivalency can take different forms, including the presence of interacting patches on a protein surface, short linear amino acid motifs, and specific amino acids within the intrinsically disordered regions of phase-separating proteins (Posey et al. 2018).
We investigated the evolution of multivalency in two well-known classes of multivalent phase-separating proteins during ∼600 million years of evolution. The first class comprises orthologs of the fungal mRNA decapping subunit 2 protein (Dcp2). Dcp2 is one of the scaffold proteins that help RNA processing bodies (P-bodies) self-assemble by liquid–liquid phase separation (Parker and Sheth 2007; Kroschwald et al. 2015; Rao and Parker 2017; Xing et al. 2020). P-bodies are conserved membrane-less eukaryotic organelles that contribute to the regulation of gene expression by participating in RNA decay and degradation (Anderson and Kedersha 2009). They also serve as mRNA storage depots when cells are stressed (Aizer et al. 2014). Dcp2 undergoes multivalent interactions using short helical leucine-rich motifs (HLMs) in its disordered C-terminal domain (Jonas and Izaurralde 2013). HLMs form 8 out of 12 identified interactions between Dcp2 and other core proteins in P-bodies (Xing et al. 2020).
The second class of proteins comprises orthologs of six members of the FET family of RNA-binding proteins, including FUS, EWS, HNRNPA1, HNRNPA3, HNRNPR, and TAF15. These proteins have a common domain architecture that consists of a prion-like domain (PLD), and other domains with RNA/DNA binding affinities (Hoell et al. 2011; Aizer et al. 2014; Schwartz et al. 2015; Svetoni et al. 2016). They contribute to DNA damage repair, transcriptional control, and the regulation of the life-time of RNAs in metazoan species (Schwartz et al. 2015). The PLD of these proteins has low sequence complexity and is enriched in few amino acids, such as asparagine, glutamine, tyrosine, and glycine (Aguzzi and Calella 2009; Franzmann and Alberti 2019). The aromatic residues within the PLD, particularly tyrosine, and arginine in RNA-binding domains, are responsible for the multivalency of these proteins (Burke et al. 2015; Patel et al. 2015; Hofweber et al. 2018). Interactions between these residues drive the phase separation of FET proteins (Wang et al. 2018).
We use the stickers-and-spacers representation (Choi et al. 2020) of phase-separating proteins throughout this work. Stickers are specific amino acids, motifs, or protein domains whose interactions drive phase separation. Spacers are the sequences that separate the stickers. The HLMs in Dcp2 and the aromatic residues in FET proteins are such stickers. For the FET proteins, we particularly focus on tyrosine residues, because their number and patterning in the sequence modulate the phase-separation propensity of these proteins (Wang et al. 2018; Martin et al. 2020; Bremer et al. 2021).
Methods
Data compilation and the generation of neutrally evolved sequences
In this study, we used 48 orthologous coding sequences of fungal Dcp2, and ∼200–300 orthologs of six members of the FET family of proteins (FUS, EWS, HNRNPA1, HNRNPA3, HNRNPR, and TAF15; overall 1480 sequenced). We downloaded these sequences from the NCBI (Pruitt et al. 2006), ENSEMBL (Hubbard et al. 2002), and KEGG (Kanehisa 2002) databases. Throughout, we worked with the amino acid sequences of these proteins, except for the simulation of neutral evolution, where we represented protein sequences on the level of DNA.
Simulation of neutrally evolved sequences
We simulated protein evolution using the Evolver package within the PAML suite (Yang 2007). In brief, Evolver uses Monte Carlo simulations to generate codon sequences using a specified phylogenetic tree with given branch lengths, nucleotide frequencies, transition/transversion bias (), and the ratio of the rate of nonsynonymous to synonymous substitutions (dN/dS; Yang 2007). To simulate neutral sequence evolution, we used the standard genetic code with codon frequencies from our study proteins sequences. Specifically, we used codon frequencies from FUS orthologs for neutral evolution in vertebrate proteins, and we used codon frequencies from the set of 48 Dcp2 sequences to model neutral evolution in fungal Dcp2. In our simulations of Dcp2 evolution, we assumed a protein length of 600 codons because the median length of C-terminal disordered domain of Dcp2 and the length of mammalian FET proteins are ∼619 and ∼518 amino acids, respectively. We used a consensus phylogenetic tree for the fungal species from the yeast genome browser (Byrne and Wolfe 2005) and for the vertebrate species from the TimeTree database (Hedges et al. 2006). In our phylogenetic trees, the branch lengths represent the expected number of nucleotide substitutions per codons. To model neutral evolution, we set dN/dS to 1 and used a transition/transversion rate ratio of 2.3 and 2.9 for fungal and mammalian sequences. We estimated these values by fitting the codon model M1 to the phylogenetic tree and the sequences of these proteins. This model assumes that all branches of the phylogenetic tree have the same rate of evolution. We evaluated the number of neutrally evolved HLMs for various values of dN/dS and the transition/transversion rate ratio to ensure that our results do not depend on the choice of these parameters (Supplementary Table S1). Overall, we generated 104 evolved sequences using this sequence evolution model.
Detection of HLMs and their distinct flanking regions
We used regular expression matching to search for HLMs that matched the LL-xφ-L pattern, where φ is a hydrophobic residue (one of the amino acids L, I, V, A, P, and F), and x represents any amino acid. To distinguish HLMs from HLM-like patterns we used the classification approaches of logistic regression and random forests implemented in the Python package scikit-learn. In these classifications, positive and the negative sets correspond to the flanking regions of HLMs and HLM-like motifs, respectively. The size of the training and the test set was 80% and 20% of the whole dataset.
Random forest classification of spacers
We used the random forest algorithm to develop a classifier of spacer conformation from the protein sequence. To this end, we used the average deviation of inter-residue distances of a spacer sequence from the same distances in a Flory Random Coil as the measure for the prediction of spacer types (Harmon et al. 2017). This deviation, known as the Δ parameter, can take positive and negative values. Disordered sequences with Δ 0.1 have the propensity to form compact conformations. We used a binary classification and classified proteins into a positive set (Δ 0.1) and a negative set (Δ 0.1). To train our classifier we used a dataset of 256 disordered sequences for which we had Δ values that had been calculated by molecular simulations (Harmon et al. 2017).
To build features for the classification, we calculated the average value of 500 physicochemical properties for each sequence in the positive and the negative sets. This yielded two feature matrices, one for sequences with Δ 0.1, and another for sequences with Δ 0.1. To apply random forest classification, we used the randomForest package of R (Liaw and Wiener 2002) and evaluated the best number of trees (nTree) and the number of variables randomly sampled at each split (mtry) in the random forest algorithm. To do so, we systematically varied nTree and mtry, and calculated the accuracy of classification with 10-fold cross-validation in three replicates. We defined accuracy as the percentage of correctly identified classes of spacers (Δ 0.1 and Δ 0.1) out of all spacers. The combination of nTree = 5000 trees and mtry = 10 variables achieved the highest accuracy of ∼88%. Here, we define accuracy as the ratio of the number of true positives to the sum of true positives and false negatives. We then used these parameters to perform 100 random forest clusterings, in which we randomly assigned proteins to the training and the testing datasets. To quantify the accuracy of classification we counted the number of true positive and false positive predictions and calculated the area under the curve. We represented these values by receiver operating characteristic curves in Supplementary Figure S2.
Phylogenetic generalized least square regression
To study the statistical association between the length of the C-terminal domain of Dcp2 sequences and the number of HLMs in this domain, we performed phylogenetic generalized least square regression. To this end, we used a consensus phylogenetic tree of 48 fungal species, as described earlier in the section “simulation of neutrally evolved sequences,” and performed the regression based on the Brownian motion process of evolution along this tree (Revell 2010; Revell 2012). We found that the slope of the number of HLMs as a function of the length of the C-terminal domain is ∼0.08 [t-value = 9.47; P(>|t|) < 10−16] compared to ∼0.09 [t-value = 76.31; P(>|t|) ∼ 0] without phylogenetic correction. We performed all statistical analyses using R.
Results and discussion
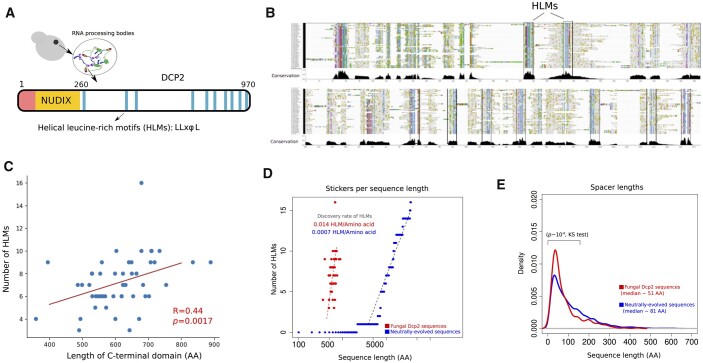
We first investigated the evolution of HLMs in 48 Dcp2 proteins of the phylum Ascomycota (Supplementary Dataset S1). HLMs lie within the disordered C-terminal domain of Dcp2 (Figure 1A, residues 229–930 in Saccharomyces cerevisiae), and take the form LL-xφ-L, where L stands for leucine, φ is a hydrophobic residue, and x represents any amino acid. We identified 347 motifs in these sequences that exactly matched the LL-xφ-L pattern (Supplementary Figure S1). As shown in Figure 1B, HLMs are the most conserved sequence segments within the intrinsically disordered C-terminal domain of Dcp2. However, their number substantially varies from a minimum of three in Lodderomyces elongisporus to a maximum of 16 in Kuraishia capsulata (Supplementary Table S1). Importantly, the number of HLMs increases with the length of the disordered C-terminal domain of a Dcp2 sequence (Figure 1C; Spearman correlation, R = 0.44, P = 0.0017). The average and median length of the spacer segments that separate HLMs are ∼70 and ∼51 amino acids. Based on these observations, we hypothesized that the scaling between the number of HLMs and the length of the disordered domain (1 HLM in ∼70 residues) reflects a requirement for a characteristic sequence length that separates sticker motifs. We tested this hypothesis by asking whether this characteristic sequence length may be subject to natural selection.
Figure 1.
The length scale of multivalent interactions is evolutionary conserved in fungi species Dcp2. (A) Architecture of Dcp2 in S. cerevisiae with the regulatory domain (in red), the NUDIX catalytic domain (in orange), and the disordered C-terminal domain (in white). Within the disordered C-terminal domain helical leucine-rich short linear motifs are responsible for the multivalency of Dcp2. (B) Multiple sequence alignment of the C-terminal domain of Dcp2 in 48 fungal species within the phylum of Ascomycota spanning ∼600 million years of evolution. HLMs, shown as blue columns, are highly conserved within the C-terminal domain of Dcp2. (C) The number of HLMs positively correlates with the length of the C-terminal domain of Dcp2 in fungi (Spearman correlation; R = 0.44, P = 0.0017). (D) The incidence of HMLs in biological sequences (shown in red) is ∼35 times higher than that of neutrally evolved sequences (shown in blue). (E) The distribution of spacer lengths (sequences that separate HLMs) in real Dcp2 sequences (shown in red), and in neutrally evolved sequences (shown in blue). We compared the two distributions and calculated the P-value for rejecting the null hypothesis that these distributions are indistinguishable by Kolmogorov–Smirnov (KS) test.
To understand the evolutionary forces that shape the scaling between the number of HLMs and the length of the C-terminal domain in Dcp2, we determined the likelihood that HLMs arise by chance through neutral evolution. To this end, we simulated neutral protein sequence evolution using realistic divergence times of real Dcp2 sequences (see Methods for details). We found that neutral evolution can indeed create motifs that exactly match known HLMs (Supplementary Figure S2 and Dataset S2), but the fraction of these neutrally evolved HLMs per unit sequence length was much lower than that of HLMs in real sequences. Specifically, neutral evolution creates only one HLM per ∼1500 amino acids. In other words, HLMs in neutrally evolving sequences are ∼35 times less frequent than in real Dcp2 sequences (Figure 1D). We recalculated the fraction of HLMs per unit of sequence length for various codon frequencies, nonsynonymous substitution rates, and values of transition/transversion bias (Supplementary Dataset S2). In all these calculations, we found a substantially higher incidence of HLMs per unit of sequence length in biological sequences compared to sequences evolved by neutral evolution (Supplementary Table S2).
We also compared the distribution of spacer lengths (segments that separate HLMs) in the C-terminal domain of Dcp2 orthologs with that of neutrally evolved sequences. The median length of spacers is 81 amino acids in neutrally evolved sequences, significantly higher than the 51 amino acids in biological Dcp2 sequences (P ∼ 10−6; Wilcoxon ran-sum test; Figure 1E). In addition, spacer lengths are significantly more variable in neutrally evolved sequences compared to the biological Dcp2 proteins (P ∼ 10−7, one-sided F-test for the equality of variances), and their length distributions are significantly different (P ∼ 10−8; Kolmogorov–Smirnov test). Altogether, these results show that evolution has not only increased the incidence of HLMs in Dcp2 sequences but also has stabilized the lengths of sequences that separate HLMs.
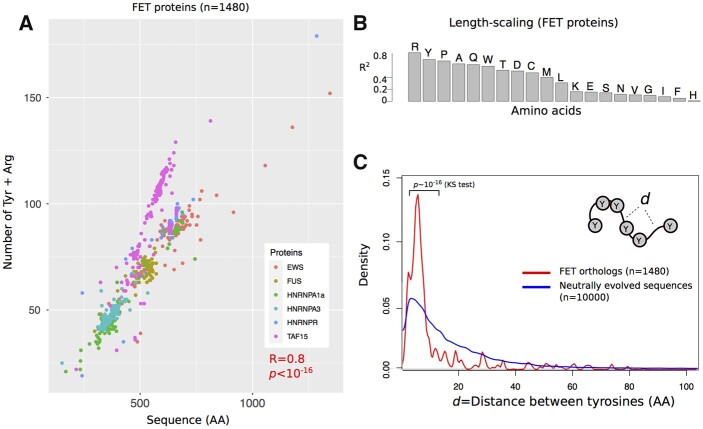
To find out whether the scaling of sticker number with the length of a disordered region is a more general property, we next studied the FET family of proteins in vertebrates. We identified ∼200–300 orthologs for each of the six FET proteins and compiled a set of 1480 sequences of these proteins (Supplementary Dataset S3). Analogous to Dcp2 and its HLMs, we observed that longer FET proteins have more arginine (R) and tyrosine (Y) sticker residues in their PLD (Figure 2A, Spearman correlation, R = 0.8, P < 10−16). Importantly, among all 20 amino acids, the number of Rs and Ys showed the highest correlation with sequence length (Figure 2B; adjusted R2 ∼ 0.81, and 0.70 in a linear model with fivefold cross-validation and 10 replicates). In sum, the scaling of multivalency with the lengths of disordered domains is not unique to Dcp2 in fungi. It also exists in the FET protein family of vertebrates.
Figure 2.
The length scale of multivalent interactions is evolutionary conserved in the FET family of vertebrate proteins. (A) The number of arginine (R) and tyrosine (Y) residues of six different FET family members and their orthologs in vertebrate species (1180 proteins overall) vs their sequence length. (B) The coefficient of determination (R2) between the number of different amino acids and the length of FET proteins and their orthologs. For a robust estimation of R2, we used a linear regression model with fivefold cross-validation that we repeated 10 times. (C) The distribution of distances between tyrosine residues in FET proteins (shown in red), and in neutrally evolved sequences (shown in blue). We compared the two distributions and calculated the P-value for rejecting the null hypothesis that these distributions are indistinguishable by Kolmogorov–Smirnov (KS) test.
We further examined the spacer lengths that separate Ys and Rs in the sequence of FET proteins to find out whether natural selection has influenced the number of stickers per unit sequence length. We compared the distance distribution of both R and Y residues in FET proteins with that of neutrally evolved sequences (see Methods for details). For both amino acids, the distribution of distances between tyrosine residues in FET proteins is significantly less variable than that of neutrally evolved sequences (see Figure 2C for spacers between tyrosine residues; P < 10−16; Kolmogorov–Smirnov test, and Supplementary Figure S3 for spacers between arginine residues). The median distance between tyrosine residues is seven amino acids for FET proteins, which is significantly less than the corresponding distance of 13 amino acids in neutrally evolving proteins (P ∼ 10−6; Wilcoxon rank-sum test). In addition, the distance distribution of FET proteins is much more sharply peaked (leptokurtic, Figure 2C) and significantly differed from neutrally evolved sequences (P ∼ 10−8; Kolmogorov–Smirnov test).
Our next analyses studied two further factors that are important in protein evolution. The first one is variation in the length of proteins caused by indels. To find out what role such length variation may play, we generated new sets of simulated sequences with two widely used models, namely the Qian–Goldstein model (Qian and Goldstein 2001) and the Zipfian model (Chang and Benner 2004), to represent the distribution of indels in evolving proteins more realistically. The Qian–Goldstein and the Zipfian models use a multiexponential distribution with four distinct components and a Zipf distribution, respectively, to model newly arising indels in protein sequences. The second factor we studied is variation in the evolutionary rates of protein residues, also known as among-site-rate-variation (Yang 1996). We used a gamma distribution with the shape parameters of 0.5 and 1 to model the variation of evolutionary rates among protein sites. In the resulting simulated sequences, spacer length varied from ∼ 28 ± 28 to 30 ± 29 amino acids, and was thus substantially greater than spacer length for FET proteins (∼13 ± 18). The distributions of spacer length were also broader (Supplementary Figure S5), and distinct from the sharply peaked distribution of spacer lengths in naturally occurring FET proteins (Supplementary Table S4, P < 10−16; Kolmogorov–Smirnov test). Altogether, these results suggest that natural selection has likely stabilized this distance distribution in FET proteins.
Next, we asked why the scaling of the number of stickers may be conserved, focusing on the hypothesis that it helps maintain a network of protein interactions that is necessary for condensation and phase separation (Harmon et al. 2017). To maintain this interaction network, it can often be energetically favorable for disordered sequences to adopt compact conformations. The reason is that this type of conformation substantially increases the chance of interactions between stickers (Harmon et al. 2017). We thus wanted to find out whether this ability exists in our proteins.
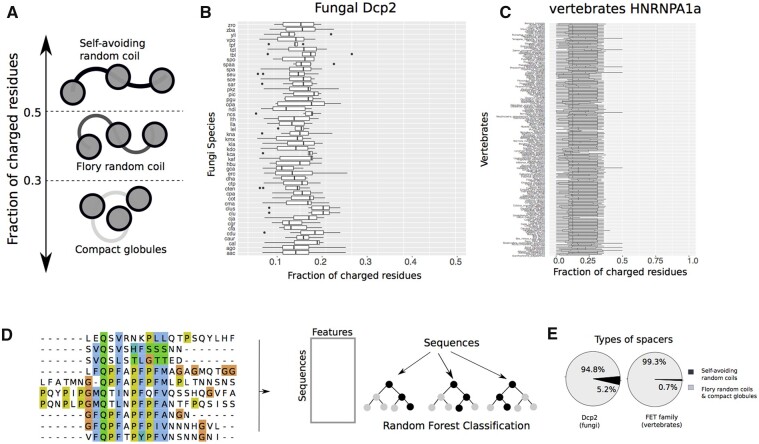
To this end, we first calculated the fraction of charged residues (FCR) in the spacers that separate HLMs in Dcp2 in the PLD of FET proteins. The FCR is a proxy for effective solvation and hence for the conformation of disordered spacers (Harmon et al. 2017). Previous studies have suggested that spacers where fewer than half of the residues are charged can self-associate, and drive the formation of a condensation-promoting network of interactions, although the determinants of spacer dimensions are inherently complex and multifaceted (Pappu et al. 2008; Das and Pappu 2013; Harmon et al. 2017; Choi et al. 2020; Bremer et al. 2021; Figure 3A). As shown in Figure 3, B and C, we found that almost all spacers in Dcp2 and FET proteins have a FCR between 0.2 and 0.4, indicating that they are able to adopt compact conformations.
Figure 3.
The disordered spacers in fungal Dcp2 and vertebrates FET proteins adopt conformations that promote phase-separation. (A) The FCR can distinguish the conformations of spacer segments in multivalent proteins. Proteins with FCR >0.5 preferentially adopt extended conformations like idealized self-avoiding random coils. Proteins with FCR <0.3 can form compact globules. Sequences with intermediate values of FCR form conformations similar to Flory random coils, where the net attractive and repulsive forces between residues and solvent molecules are in balance. The FCR for (B) fungal Dcp2 sequences, and (C) vertebrate HNRNPA1a, a member of the FET family. (D) Schematic for machine-learning random-forest classification to classify spacer types from their amino acid sequence. In brief, we used the sequences of naturally occurring disordered sequences that connect different domains, calculated the average of 500 amino acid properties for each sequence, and used this dataset to classify these sequences into the two categories of self-avoiding random coils, and Flory-random coils and compact globules. (E) The fraction of spacers that adopt compact conformations (Flory random coils, and compact globules), and those that adopt extended conformations (self-avoiding random coils) in fungal Dcp2 and vertebrate FET proteins.
To complement our analysis of the fraction of charge residues in Dcp2 sequences, we further identified the molecular features of Dcp2 that have likely evolved under selection using the method proposed by Zarin et al. (2017, 2019) In brief, this method compares the distribution of different molecular features to a null expectation that is generated by simulating the evolution of disordered proteins. In this method, deviations in each molecular feature between naturally occurring orthologs of a protein of interest and a set of simulated sequences (measured by a z-score) indicate that selection has likely acted on that specific molecular feature. Consistent with our observations thus far, we found that the FCR is under selection in the evolution of Dcp2 (Supplementary Figure S6, z-score = −11.35, P < 10−16; standard normal distribution).
Second, we predicted a structural feature of disordered sequences known as the Δ-parameter. This parameter is the average difference between the inter-residue distances of a disordered sequence and the corresponding distances of a typical Flory random coil (Harmon et al. 2017). It is calculated by molecular simulations (see Harmon et al. 2017) for a comprehensive description of the relevant procedures). Flory random coils are an idealized kind of disordered sequences in which the attractive and repulsive forces between residues and solvent molecules are at balance. Spacers that self-associate and promote phase separation are characterized by Δ 0.1. As Δ increases beyond 0.1, spacers adopt more extended conformations, resembling another type of idealized sequence known as a self-avoiding random coil (Figure 3A).
We developed a sequence-based classifier of Δ using a random forest algorithm (Figure 3D), which classifies spacers based on their amino acid properties into two classes, those with Δ > 0.1, and those with Δ 0.1 (see Methods for details). We trained this classifier on a dataset of 256 naturally occurring disordered sequences whose Δ values had been previously calculated by molecular simulations (Harmon et al. 2017).
This classifier achieved an accuracy of ∼0.88 in 100 independent runs with the data split into a training set (80% of the data) and a testing set (20%) (Supplementary Figure S4, see Methods for details). It revealed three most important amino acid features for classifications. The first is the similarity of the composition of spacers to the composition of mitochondrial proteins. The second is the propensity to form beta-structures. The third is the transfer free energy of peptides from bilayer interfaces to water (Supplementary Table S4). The compositions of compact spacers, i.e., spacers with Δ 0.1, were on average more like those of mitochondrial proteins (with a higher fraction of N, L, I, L, S, T, F, Y). In addition, such spacers had a higher propensity to form beta structures, and a lower propensity to leave bilayer interfaces and enter aqueous solutions.
Note that our classification of spacer conformations using amino acid propensities was substantially more accurate (accuracy ∼88%) than that of classification with the FCR alone (accuracy ∼50%). This result further supports the notion that sequence determinants of chain compaction are complex and not just a function of the FCR (Das and Pappu 2013). Indeed, sequences with a FCR far below 0.5 (Fuertes et al. 2017; Riback et al. 2017), and even sequences without charged residues, such as Gly-Ser linkers (Sørensen and Kjaergaard 2019; Dyla and Kjaergaard 2020; Tsang et al. 2020), can behave as Flory random coils.
Using our random forest classifier, we found that ∼94.8% of all spacers in Dcp2 have a predicted value of Δ below 0.1. We repeated this analysis for the spacers in the PLD of the FET proteins and found that in these proteins too, most spacers (∼99.3%) have a predicted Δ 0.1. Altogether, these results indicate that both fungal Dcp2 sequences and vertebrate FET proteins have spacers that can self-associate and promote phase separation in these proteins.
In summary, our work reveals that evolution has maintained a characteristic length scale of multivalent sticker sequences in two classes of multivalent proteins during ∼600 million years of evolution. Our results extend previous observations that the number and patterning of stickers, as well as the composition of spacers within intrinsically disordered domains of phase-separating proteins, are important features and likely conserved in their evolution. For example, Martin et al. showed that a uniform patterning of tyrosine residues in some FET proteins promotes phase separation, and inhibits the aggregation of these proteins (Martin et al. 2020). A further compositional analysis of the PLD of hnRNPA1 shows that the compositional biases of this protein domain are similar across PLDs of its distant homologs (Bremer et al. 2021). Also, Schmidt et al. (2019) demonstrated that the number and spacing of sticker hydrophobic clusters in TDP-43, another member of the FET family, are evolutionary conserved. Such conservation reflects the optimal condition for condensate formation and localization of this protein to the nucleus.
The substantial variation in the sequence length and multivalency of both of our phase-separating protein classes seems surprising from the standpoint of polymer physics, if one assumes that the saturation concentration of our phase-separating proteins is under selection. Increasing the length of associative polymers while keeping the density of stickers fixed will decrease the driving force for phase separation, because a longer polymer face a higher entropic barrier to phase separate. Therefore, longer multivalent proteins should have a lower propensity to phase separate. However, this lower propensity can be compensated in other ways, such as a change in gene expression, the composition of spacers, or post-translational modifications. Indeed, such compensation between the length of an intrinsically disordered protein and its composition has been observed recently in the adenovirus early gene 1A protein (Gonzalez-Foutel et al. 2021). In addition, it is also possible that the saturation concentration of phase-separating proteins is not under selection, and that the phase-separation behavior of our proteins deviates from that of homo-polymers. Future computational and experimental work will be needed to study the consequences of variation in multivalency.
Dcp2 plays an important role in the assembly of RNA P-bodies, and FET proteins play such a role in the assembly of stress granules. Biomolecular condensates like these are sensitive to environmental stressors such as heat shock and energy depletion (O’Connell et al. 2014; Boeynaems et al. 2018; Franzmann and Alberti 2019; Zarin et al. 2019). Our results thus also raise the intriguing possibility that evolution may have modulated the multivalency of proteins in membrane-less organelles to help organisms cope with new environments. Two recently studied proteins that support this possibility are the fungal translation initiation factor Ded1p, and the plant prion-like protein FLOE1, which regulates seed germination when plants face water stress. Specifically, the temperature onset of phase separation of Ded1p correlates with the maximum growth temperature of three fungal species (Iserman et al. 2020). FLOE1, which phase separates upon hydration in Arabidopsis thaliana, shows natural variation in this propensity that correlates with enhanced germination. The molecular causes of such adaptations pose an exciting problem for future work.
Data availability
Scripts and input files for classification, evolutionary simulations, and statistical analyses are available at: https://github.com/dasmeh/multivalency_evolution
Supplementary material is available at GENETICS online.
Supplementary Material
Acknowledgments
The authors would like to thank Simon Alberti for careful reading of the manuscript and for helpful discussions on the evolution of liquid–liquid phase separation. The authors thank the anonymous reviewers for their careful reading of our manuscript and their constructive and insightful comments.
Funding
This project has received funding from the European Research Council under Grant Agreement No. 739874. We would also like to acknowledge support by Swiss National Science Foundation grant 31003A_172887 and by the University Priority Research Program in Evolutionary Biology at the University of Zurich.
Conflicts of interest
The authors declare that there is no conflict of interest.
Literature cited
- Aguzzi A, Calella AM. 2009. Prions: protein aggregation and infectious diseases. Physiol Rev. 89:1105–1152. [DOI] [PubMed] [Google Scholar]
- Aizer A, Kalo A, Kafri P, Shraga A, Ben-Yishay R, et al. 2014. Quantifying mRNA targeting to P-bodies in living human cells reveals their dual role in mRNA decay and storage. J Cell Sci. 127:4443–4456. [DOI] [PubMed] [Google Scholar]
- Anderson P, Kedersha N. 2009. RNA granules: post-transcriptional and epigenetic modulators of gene expression. Nat Rev Mol Cell Biol. 10:430–436. [DOI] [PubMed] [Google Scholar]
- Banani SF, Lee HO, Hyman AA, Rosen MK. 2017. Biomolecular condensates: organizers of cellular biochemistry. Nat Rev Mol Cell Biol. 18:285–298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boeynaems S, Alberti S, Fawzi NL, Mittag T, Polymenidou M, et al. 2018. Protein phase separation: a new phase in cell biology. Trends Cell Biol. 28:420–435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brangwynne CP, Tompa P, Pappu RV. 2015. Polymer physics of intracellular phase transitions. Nature Phys. 11:899–904. [Google Scholar]
- Bremer A, Farag M, Borcherds WM, Peran I, Martin EW, et al. 2021. Deciphering how naturally occurring sequence features impact the phase behaviors of disordered prion-like domains. doi:10.1101/2021.01.01.425046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burke KA, Janke AM, Rhine CL, Fawzi NL. 2015. Residue-by-residue view of in vitro FUS granules that bind the C-terminal domain of RNA polymerase II. Mol Cell. 60:231–241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Byrne KP, Wolfe KH. 2005. The Yeast Gene Order Browser: combining curated homology and syntenic context reveals gene fate in polyploid species. Genome Res. 15:1456–1461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang MS, Benner SA. 2004. Empirical analysis of protein insertions and deletions determining parameters for the correct placement of gaps in protein sequence alignments. J Mol Biol. 341:617–631. [DOI] [PubMed] [Google Scholar]
- Choi J-M, Holehouse AS, Pappu RV. 2020. Physical principles underlying the complex biology of intracellular phase transitions. Annu Rev Biophys. 49:107–133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Das RK, Pappu RV. 2013. Conformations of intrinsically disordered proteins are influenced by linear sequence distributions of oppositely charged residues. Proc Natl Acad Sci U S A. 110:13392–13397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dyla M, Kjaergaard M. 2020. Intrinsically disordered linkers control tethered kinases via effective concentration. Proc Natl Acad Sci U S A. 117:21413–21419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franzmann TM, Alberti S. 2019. Prion-like low-complexity sequences: key regulators of protein solubility and phase behavior. J Biol Chem. 294:7128–7136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fuertes G, Banterle N, Ruff KM, Chowdhury A, Mercadante D, et al. 2017. Decoupling of size and shape fluctuations in heteropolymeric sequences reconciles discrepancies in SAXS vs. FRET measurements. Proc Natl Acad Sci U S A. 114:E6342–E6351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gonzalez-Foutel NS, Borcherds WM, Glavina J, Barrera-Vilarmau S, Sagar A, et al. 2021. Conformational buffering underlies functional selection in intrinsically disordered protein regions. doi:10.1101/2021.05.14.444182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harmon TS, Holehouse AS, Rosen MK, Pappu RV. 2017. Intrinsically disordered linkers determine the interplay between phase separation and gelation in multivalent proteins. Elife. 6:e30294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hedges SB, Dudley J, Kumar S. 2006. TimeTree: a public knowledge-base of divergence times among organisms. Bioinformatics. 22:2971–2972. [DOI] [PubMed] [Google Scholar]
- Hoell JI, Larsson E, Runge S, Nusbaum JD, Duggimpudi S, et al. 2011. RNA targets of wild-type and mutant FET family proteins. Nat Struct Mol Biol. 18:1428–1431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hofweber M, Hutten S, Bourgeois B, Spreitzer E, Niedner-Boblenz A, et al. 2018. Phase separation of FUS is suppressed by its nuclear import receptor and arginine methylation. Cell. 173:706–719.e13. [DOI] [PubMed] [Google Scholar]
- Hubbard T, Barker D, Birney E, Cameron G, Chen Y, et al. 2002. The Ensembl genome database project. Nucleic Acids Res. 30:38–41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iserman C, Altamirano CD, Jegers C, Friedrich U, Zarin T, et al. 2020. Condensation of Ded1p promotes a translational switch from housekeeping to stress protein production. Cell. 181:818–831.e19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jonas S, Izaurralde E. 2013. The role of disordered protein regions in the assembly of decapping complexes and RNP granules. Genes Dev. 27:2628–2641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kanehisa M, Goto, S. 2000. KEGG: Kyoto Encyclopedia of Genes and Genomes. Nucleic Acids Res. 28, 27–30. [DOI] [PMC free article] [PubMed]
- Kroschwald S, Maharana S, Mateju D, Malinovska L, Nüske E, et al. 2015. Promiscuous interactions and protein disaggregases determine the material state of stress-inducible RNP granules. Elife. 4:e06807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li P, Banjade S, Cheng H-C, Kim S, Chen B, et al. 2012. Phase transitions in the assembly of multivalent signalling proteins. Nature. 483:336–340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liaw A, Wiener M. 2002. Classification and regression by randomForest. R News. 2:18–22. [Google Scholar]
- Martin EW, Holehouse AS, Peran I, Farag M, Incicco JJ, et al. 2020. Valence and patterning of aromatic residues determine the phase behavior of prion-like domains. Science. 367:694–699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Connell JD, Tsechansky M, Royal A, Boutz DR, Ellington AD, et al. 2014. A proteomic survey of widespread protein aggregation in yeast. Mol Biosyst. 10:851–861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pappu RV, Wang X, Vitalis A, Crick SL. 2008. A polymer physics perspective on driving forces and mechanisms for protein aggregation. Arch Biochem Biophys. 469:132–141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parker R, Sheth U. 2007. P bodies and the control of mRNA translation and degradation. Mol Cell. 25:635–646. [DOI] [PubMed] [Google Scholar]
- Patel A, Lee HO, Jawerth L, Maharana S, Jahnel M, et al. 2015. A liquid-to-solid phase transition of the ALS protein FUS accelerated by disease mutation. Cell. 162:1066–1077. [DOI] [PubMed] [Google Scholar]
- Posey AE, Holehouse AS, Pappu RV. 2018. Phase separation of intrinsically disordered proteins. Methods Enzymol. 611:1–30. [DOI] [PubMed] [Google Scholar]
- Pruitt KD, Tatusova T, Maglott DR. 2006. NCBI reference sequences (RefSeq): a curated non-redundant sequence database of genomes, transcripts and proteins. Nucleic Acids Res. 35: D61–D65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qian B, Goldstein RA. 2001. Distribution of Indel lengths. Proteins. 45:102–104. [DOI] [PubMed] [Google Scholar]
- Rao BS, Parker R. 2017. Numerous interactions act redundantly to assemble a tunable size of P bodies in Saccharomyces cerevisiae. Proc Natl Acad Sci U S A. 114:E9569–E9578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Revell LJ. 2010. Phylogenetic signal and linear regression on species data. Methods Ecol Evolut. 1:319–329. [Google Scholar]
- Revell LJ. 2012. Phytools: an R package for phylogenetic comparative biology (and other things). Methods Ecol Evolut. 3:217–223. [Google Scholar]
- Riback JA, Katanski CD, Kear-Scott JL, Pilipenko EV, Rojek AE, et al. 2017. Stress-triggered phase separation is an adaptive, evolutionarily tuned response. Cell. 168:1028–1040.e19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmidt HB, Barreau A, Rohatgi R. 2019. Phase separation-deficient TDP43 remains functional in splicing. Nat Commun. 10:1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwartz JC, Cech TR, Parker RR. 2015. Biochemical properties and biological functions of FET proteins. Annu Rev Biochem. 84:355–379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sørensen CS, Kjaergaard M. 2019. Effective concentrations enforced by intrinsically disordered linkers are governed by polymer physics. Proc Natl Acad Sci U S A. 116:23124–23131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Svetoni F, Frisone P, Paronetto MP. 2016. Role of FET proteins in neurodegenerative disorders. RNA Biol. 13:1089–1102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsang B, Pritišanac I, Scherer SW, Moses AM, Forman-Kay JD. 2020. Phase separation as a missing mechanism for interpretation of disease mutations. Cell. 183:1742–1756. [DOI] [PubMed] [Google Scholar]
- Wang J, Choi J-M, Holehouse AS, Lee HO, Zhang X, et al. 2018. A molecular grammar governing the driving forces for phase separation of prion-like RNA binding proteins. Cell. 174:688–699.e16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xing W, Muhlrad D, Parker R, Rosen MK. 2020. A quantitative inventory of yeast P body proteins reveals principles of composition and specificity. Elife. 9:e56525. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Z. 1996. Among-site rate variation and its impact on phylogenetic analyses. Trends Ecol Evol. 11:367–372. [DOI] [PubMed] [Google Scholar]
- Yang Z. 2007. PAML 4: phylogenetic analysis by maximum likelihood. Mol Biol Evol. 24:1586–1591. [DOI] [PubMed] [Google Scholar]
- Zarin T, Strome B, Ba ANN, Alberti S, Forman-Kay JD, et al. 2019. Proteome-wide signatures of function in highly diverged intrinsically disordered regions. Elife. 8:e46883:1–26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zarin T, Tsai CN, Ba ANN, Moses AM. 2017. Selection maintains signaling function of a highly diverged intrinsically disordered region. Proc Natl Acad Sci U S A. 114:E1450–E1459. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Scripts and input files for classification, evolutionary simulations, and statistical analyses are available at: https://github.com/dasmeh/multivalency_evolution
Supplementary material is available at GENETICS online.