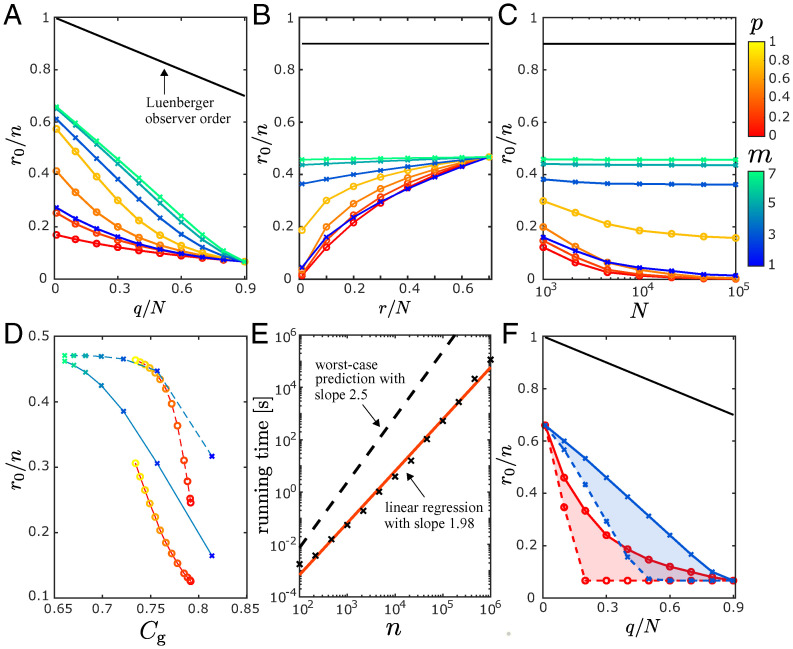
Fig. 3.

Minimum-order functional observer design in large-scale networks. (A–C) Minimum functional observer order r₀ (normalized by the system dimension $n=3N$) as a function of the normalized number of sensor nodes q / N (A), the normalized number of target nodes r / N (B), and the network size N (C). The results are shown for random placement of sensor and target nodes in directed SW and SF networks (color coded by the respective parameters p and m). The other parameters are set to $(N,r)=({10}^4,0.1N)$ for A, $(N,q)=({10}^4,0.3N)$ for B, and $(q,r)=(0.3N,100)$ for C. The black lines indicate the Luenberger observer order $(n-q)$ for comparison. (D) Normalized order $r_0/n$ in directed (solid lines) and undirected (dashed lines) SW and SF networks as a function of the generalized clustering of the corresponding undirected graph (Materials and Methods), color coded by p and m for $(N,q,r)=({10}^4,0.3N,0.1N)$. (E) Running time of Algorithm 2 as a function of n in directed SW networks for $(q,r,p)=(0.3N,0.1N,0.2)$. The simulations were implemented in MATLAB, and each network realization was run on a single core of an Intel Xeon Processor E7-8867 v4 at 2.4 GHz. (F) Normalized order $r_0/n$ as a function of q / N in undirected SW (red; p = 0) and SF (blue; m = 3) networks for randomly (solid lines) and optimally (dashed lines) placed sensors, where $(N,r)=(100,0.1N)$. In all panels, each data point corresponds to an average over 100 independent realizations of the network, target placement, and sensor placement (except for the optimal placement in F).