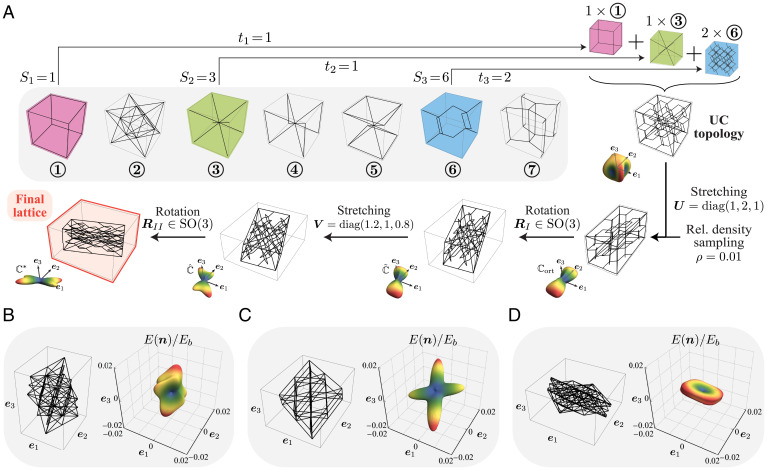
Fig. 1.

Generation of a diverse truss dataset. (A) Sequence of generating different lattice realizations, showing the corresponding elastic surfaces at each stage. First, a topology is randomly drawn by superimposing and tessellating up to three unique elementary topologies (45). Next, its geometry is transformed by four affine deformations to break the orthotropic symmetry and enable shear–shear and shear–normal coupling, while maintaining continuous design/stiffness spaces. Elastic surfaces were obtained by FE simulations and qualitatively illustrate the effective directional Young’s modulus $E(\mathit{n})$ for all directions $\mathit{n}\in S^2$ in the Cartesian basis $\{{\mathit{e}}_1,{\mathit{e}}_2,{\mathit{e}}_3\}$. (B–D) Examples of truss UC realizations, showcasing the diverse elastic responses (normalized by the base material’s Young’s modulus E_b). While all three shown examples have a relative density $\rho =0.05$, the actual dataset randomly samples ρ to cover a large range of stiffness responses.