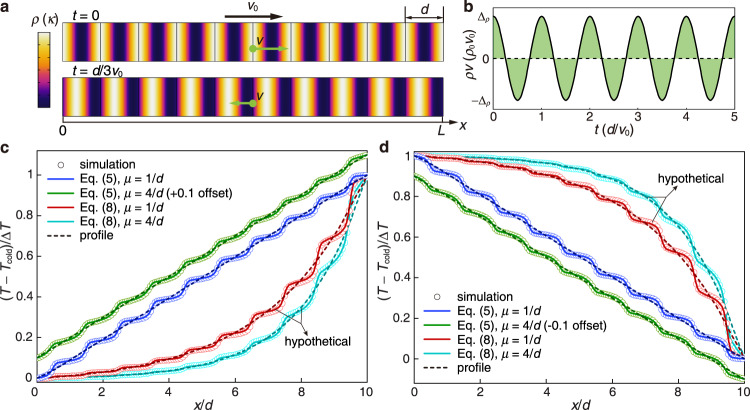
Fig. 2. Heat transfer under 1D density modulation.
a Density ρ and thermal conductivity κ (color maps) move as traveling waves at speed v0 with wavelength d. To achieve density modulation, actual mass movements (green arrows) at speed v must exist. b The total mass flux in a time period should be zero to keep a cyclic and close setup. c, d Backward (c) and forward (d) temperature distributions of the system (Eq. (5)) at t = Nd/v0 (N is a large enough integer to achieve time-harmonic steady state), compared with those of a virtual system without mass movements (Eq. (8)). Scatter points are simulated results, lines are analytical results, and dashed lines are analytical solutions of the homogenized profiles. For clarity, the results of Eq. (5) at modulating speed μ = 4/d are shifted to have ±0.1 offsets.