Figure 3:

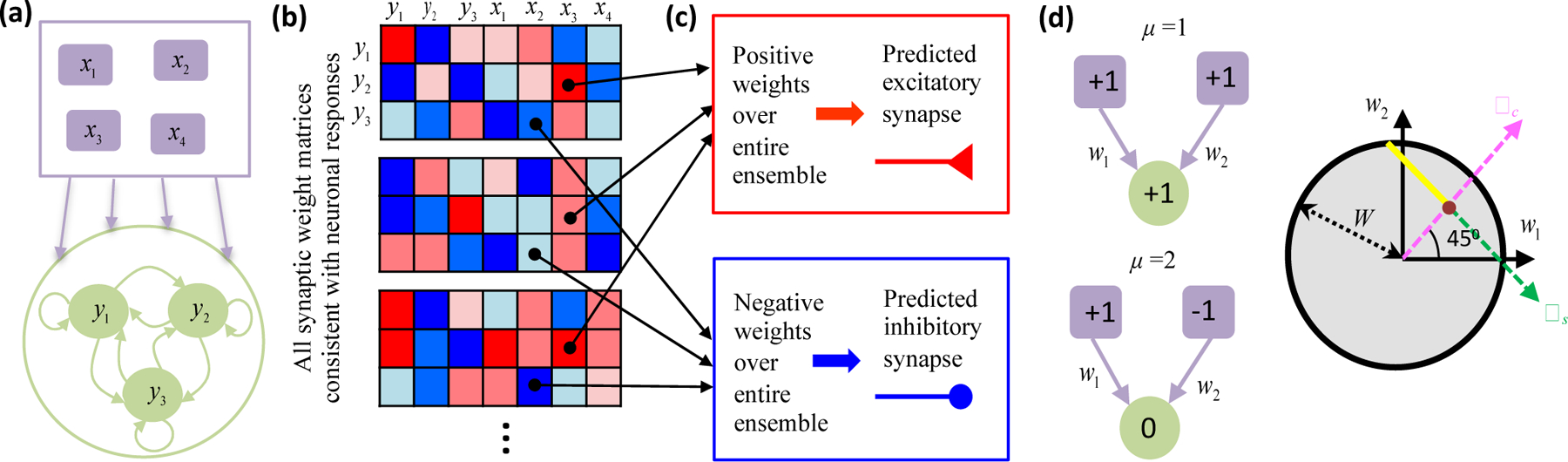
(a) Biswas and Fitzgerald [47] first specified steady-state responses of a recurrent threshold-linear neural network (green neurons) receiving feedforward input (purple neurons). (b) Assuming that the number of specified responses does not exceed the number of synapses onto each neuron, they then found all synaptic weight matrices having fixed points at the specified responses. Red (blue) matrix elements denote positive (negative) synaptic weights. (c) When a weight was consistently positive (or consistently negative) across all possibilities, then the model needed a nonzero synaptic connection to generate the responses. The model thus predicts that this synapse should exist experimentally. (d) The threshold nonlinearity provides flexibility, but some features of connectivity can nevertheless be definite. (d, left) Cartoon depicting steady state response patterns of a simple feedforward network under two stimulus conditions. The driven neuron responds in one stimulus condition (top) but is silent in the other (bottom). Numbers inside the neurons indicate activity levels. (d, right) The circle represents the two-dimensional space of allowed synaptic weights, assuming that the total weight norm is bounded by W. The two response conditions would uniquely determine the weight magnitudes in a linear neural network (brown dot, w₁ = w₂ = 1/2). However, the driven neuron’s silent response in the threshold-linear neural network only implies that the synaptic weight component along the ω_s direction is negative, because any sub-threshold input would suffice. All points on the semi-infinite yellow line thus reproduce the observed responses. Biswas and Fitzgerald refer to the ω_s direction as a “semi-constrained” dimension in the solution space. Despite this flexibility, all model solutions require w₂ > 0.