An introduction to inverse probability of treatment weighting in observational research

ABSTRACT

In this article we introduce the concept of inverse probability of treatment weighting (IPTW) and describe how this method can be applied to adjust for measured confounding in observational research, illustrated by a clinical example from nephrology. IPTW involves two main steps. First, the probability—or propensity—of being exposed to the risk factor or intervention of interest is calculated, given an individual’s characteristics (i.e. propensity score). Second, weights are calculated as the inverse of the propensity score. The application of these weights to the study population creates a pseudopopulation in which confounders are equally distributed across exposed and unexposed groups. We also elaborate on how weighting can be applied in longitudinal studies to deal with informative censoring and time-dependent confounding in the setting of treatment-confounder feedback.

Box 1. Key concepts

• Inverse probability of treatment weighting (IPTW) can be used to adjust for confounding in observational studies. IPTW uses the propensity score to balance baseline patient characteristics in the exposed and unexposed groups by weighting each individual in the analysis by the inverse probability of receiving his/her actual exposure.

• It is considered good practice to assess the balance between exposed and unexposed groups for all baseline characteristics both before and after weighting.

• An important methodological consideration is that of extreme weights. These can be dealt with either weight stabilization and/or weight truncation.

• To adjust for confounding measured over time in the presence of treatment-confounder feedback, IPTW can be applied to appropriately estimate the parameters of a marginal structural model. Weights are calculated at each time point as the inverse probability of receiving his/her exposure level, given an individual’s previous exposure history, the previous values of the time-dependent confounder and the baseline confounders.

• In time-to-event analyses, inverse probability of censoring weights can be used to account for informative censoring by up-weighting those remaining in the study, who have similar characteristics to those who were censored.

INTRODUCTION

Randomized controlled trials (RCTs) are considered the gold standard for studying the efficacy of an intervention [1]. Randomization highly increases the likelihood that both intervention and control groups have similar characteristics and that any remaining differences will be due to chance, effectively eliminating confounding. Any difference in the outcome between groups can then be attributed to the intervention and the effect estimates may be interpreted as causal. However, many research questions cannot be studied in RCTs, as they can be too expensive and time-consuming (especially when studying rare outcomes), tend to include a highly selected population (limiting the generalizability of results) and in some cases randomization is not feasible (for ethical reasons).

In contrast, observational studies suffer less from these limitations, as they simply observe unselected patients without intervening [2]. Observational research may be highly suited to assess the impact of the exposure of interest in cases where randomization is impossible, for example, when studying the relationship between body mass index (BMI) and mortality risk. However, because of the lack of randomization, a fair comparison between the exposed and unexposed groups is not as straightforward due to measured and unmeasured differences in characteristics between groups. Certain patient characteristics that are a common cause of both the observed exposure and the outcome may obscure—or confound—the relationship under study [3], leading to an over- or underestimation of the true effect [3].

To control for confounding in observational studies, various statistical methods have been developed that allow researchers to assess causal relationships between an exposure and outcome of interest under strict assumptions. Besides traditional approaches, such as multivariable regression [4] and stratification [5], other techniques based on so-called propensity scores, such as inverse probability of treatment weighting (IPTW), have been increasingly used in the literature. In short, IPTW involves two main steps. First, the probability—or propensity—of being exposed, given an individual’s characteristics, is calculated. This is also called the propensity score. Second, weights for each individual are calculated as the inverse of the probability of receiving his/her actual exposure level. The application of these weights to the study population creates a pseudopopulation in which measured confounders are equally distributed across groups. In this article we introduce the concept of IPTW and describe in which situations this method can be applied to adjust for measured confounding in observational research, illustrated by a clinical example from nephrology. We also demonstrate how weighting can be applied in longitudinal studies to deal with time-dependent confounding in the setting of treatment-confounder feedback and informative censoring.

Case study—Introduction

We will illustrate the use of IPTW using a hypothetical example from nephrology. In this example we will use observational European Renal Association–European Dialysis and Transplant Association Registry data to compare patient survival in those treated with extended-hours haemodialysis (EHD) (>6-h sessions of HD) with those treated with conventional HD (CHD) among European patients [6]. In this example, patients treated with EHD were younger, suffered less from diabetes and various cardiovascular comorbidities, had spent a shorter time on dialysis and were more likely to have received a kidney transplantation in the past compared with those treated with CHD. For these reasons, the EHD group has a better health status and improved survival compared with the CHD group, which may obscure the true effect of treatment modality on survival. These variables, which fulfil the criteria for confounding, need to be dealt with accordingly, which we will demonstrate in the paragraphs below using IPTW.

Propensity scores

The propensity score was first defined by Rosenbaum and Rubin in 1983 as ‘the conditional probability of assignment to a particular treatment given a vector of observed covariates’ [7]. In other words, the propensity score gives the probability (ranging from 0 to 1) of an individual being exposed (i.e. assigned to the intervention or risk factor) given their baseline characteristics. The aim of the propensity score in observational research is to control for measured confounders by achieving balance in characteristics between exposed and unexposed groups. By accounting for any differences in measured baseline characteristics, the propensity score aims to approximate what would have been achieved through randomization in an RCT (i.e. pseudorandomization). In contrast to true randomization, it should be emphasized that the propensity score can only account for measured confounders, not for any unmeasured confounders [8].

Assuming a dichotomous exposure variable, the propensity score of being exposed to the intervention or risk factor is typically estimated for each individual using logistic regression, although machine learning and data-driven techniques can also be useful when dealing with complex data structures [9, 10]. The calculation of propensity scores is not only limited to dichotomous variables, but can readily be extended to continuous or multinominal exposures [11, 12], as well as to settings involving multilevel data or competing risks [12, 13]. Although there is some debate on the variables to include in the propensity score model, it is recommended to include at least all baseline covariates that could confound the relationship between the exposure and the outcome, following the criteria for confounding [3]. In addition, covariates known to be associated only with the outcome should also be included [14, 15], whereas inclusion of covariates associated only with the exposure should be avoided to avert an unnecessary increase in variance [14, 16]. Any interactions between confounders and any non-linear functional forms should also be accounted for in the model. Importantly, prognostic methods commonly used for variable selection, such as P-value-based methods, should be avoided, as this may lead to the exclusion of important confounders. Instead, covariate selection should be based on existing literature and expert knowledge on the topic. Confounders may be included even if their P-value is >0.05. It should also be noted that, as per the criteria for confounding, only variables measured before the exposure takes place should be included, in order not to adjust for mediators in the causal pathway.

After correct specification of the propensity score model, at any given value of the propensity score, individuals will have, on average, similar measured baseline characteristics (i.e. covariate balance). The propensity score can subsequently be used to control for confounding at baseline using either stratification by propensity score, matching on the propensity score, multivariable adjustment for the propensity score or through weighting on the propensity score. Several weighting methods based on propensity scores are available, such as fine stratification weights [17], matching weights [18], overlap weights [19] and inverse probability of treatment weights—the focus of this article. These different weighting methods differ with respect to the population of inference, balance and precision. A thorough overview of these different weighting methods can be found elsewhere [20].

Case study—Propensity scores

In our example, we start by calculating the propensity score using logistic regression as the probability of being treated with EHD versus CHD. We include in the model all known baseline confounders as covariates: patient sex, age, dialysis vintage, having received a transplant in the past and various pre-existing comorbidities. In addition, as we expect the effect of age on the probability of EHD will be non-linear, we include a cubic spline for age. We also include an interaction term between sex and diabetes, as—based on the literature—we expect the confounding effect of diabetes to vary by sex. The logistic regression model gives the probability, or propensity score, of receiving EHD for each patient given their characteristics.

IPTW

IPTW uses the propensity score to balance baseline patient characteristics in the exposed (i.e. those who received treatment) and unexposed groups by weighting each individual by the inverse probability of receiving his/her actual treatment [21]. Weights are calculated for each individual as $1/\mathrm{propensity}\mathrm{ }\mathrm{score}$ for the exposed group and $1/(1-\mathrm{propensity}\mathrm{ }\mathrm{score})$ for the unexposed group. As such, exposed individuals with a lower probability of exposure (and unexposed individuals with a higher probability of exposure) receive larger weights and therefore their relative influence on the comparison is increased. Subsequent inclusion of the weights in the analysis renders ‘assignment’ to either the exposed or unexposed group independent of the variables included in the propensity score model. For example, suppose that the percentage of patients with diabetes at baseline is lower in the exposed group (EHD) compared with the unexposed group (CHD) and that we wish to balance the groups with regards to the distribution of diabetes. In patients with diabetes, the probability of receiving EHD treatment is 25% (i.e. a propensity score of 0.25). In order to balance the distribution of diabetes between the EHD and CHD groups, we can up-weight each patient in the EHD group by taking the inverse of the propensity score. In patients with diabetes this is $1/0.25 = 4$. Conceptually this weight now represents not only the patient him/herself, but also three additional patients, thus creating a so-called pseudopopulation. Similarly, weights for CHD patients are calculated as 1/(1 − 0.25) = 1.33. In this weighted population, diabetes is now equally distributed across the EHD and CHD treatment groups and any treatment effect found may be considered independent of diabetes (Figure 1). Conceptually IPTW can be considered mathematically equivalent to standardization.

FIGURE 1:

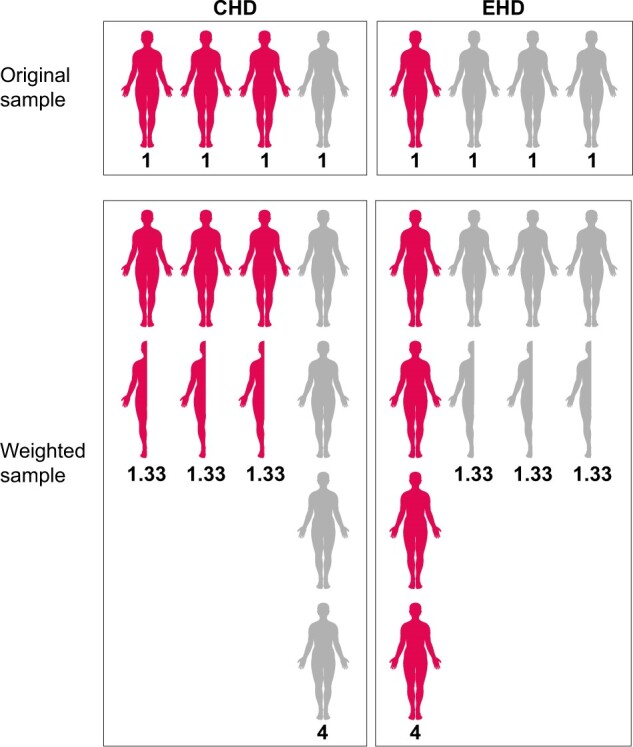
Example of balancing the proportion of diabetes patients between the exposed (EHD) and unexposed groups (CHD), using IPTW. In this example, the probability of receiving EHD in patients with diabetes (red figures) is 25%. The inverse probability weight in patients receiving EHD is therefore 1/0.25 = 4 and 1/(1 − 0.25) = 1.33 in patients receiving CHD. Conversely, the probability of receiving EHD treatment in patients without diabetes (white figures) is 75%. The inverse probability weight in patients without diabetes receiving EHD is therefore 1/0.75 = 1.33 and 1/(1 − 0.75) = 4 in patients receiving CHD. In the original sample, diabetes is unequally distributed across the EHD and CHD groups. After applying the inverse probability weights to create a weighted pseudopopulation, diabetes is equally distributed across treatment groups (50% in each group).

Percentage of diabetes	CHD	EHD
Original sample	3/4 = 75%	1/4 = 25%
Weighted sample	4/8 = 50%	4/8 = 50%

As IPTW aims to balance patient characteristics in the exposed and unexposed groups, it is considered good practice to assess the standardized differences between groups for all baseline characteristics both before and after weighting [22]. The table standardized difference compares the difference in means between groups in units of standard deviation (SD) and can be calculated for both continuous and categorical variables [23]. The advantage of checking standardized mean differences is that it allows for comparisons of balance across variables measured in different units. As a rule of thumb, a standardized difference of <10% may be considered a negligible imbalance between groups. P-values should be avoided when assessing balance, as they are highly influenced by sample size (i.e. even a negligible difference between groups will be statistically significant given a large enough sample size). If the standardized differences remain too large after weighting, the propensity model should be revisited (e.g. by including interaction terms, transformations, splines) [24, 25]. Besides having similar means, continuous variables should also be examined to ascertain that the distribution and variance are similar between groups. This can be checked using box plots and/or tested using the Kolmogorov–Smirnov test [25].

An important methodological consideration of the calculated weights is that of extreme weights [26]. In studies with large differences in characteristics between groups, some patients may end up with a very high or low probability of being exposed (i.e. a propensity score very close to 0 for the exposed and close to 1 for the unexposed). In these individuals, taking the inverse of the propensity score may subsequently lead to extreme weight values, which in turn inflates the variance and confidence intervals of the effect estimate. This may occur when the exposure is rare in a small subset of individuals, which subsequently receives very large weights, and thus have a disproportionate influence on the analysis. As these patients represent only a small proportion of the target study population, their disproportionate influence on the analysis may affect the precision of the average effect estimate. In such cases the researcher should contemplate the reasons why these odd individuals have such a low probability of being exposed and whether they in fact belong to the target population or instead should be considered outliers and removed from the sample. After all, patients who have a 100% probability of receiving a particular treatment would not be eligible to be randomized to both treatments. In addition, extreme weights can be dealt with through either weight ‘stabilization’ and/or weight truncation. Weight stabilization can be achieved by replacing the numerator (which is 1 in the unstabilized weights) with the crude probability of exposure (i.e. given by the propensity score model without covariates). In case of a binary exposure, the numerator is simply the proportion of patients who were exposed. Stabilized weights can therefore be calculated for each individual as $\mathrm{proportion}\mathrm{ }\mathrm{exposed}/\mathrm{propensity}\mathrm{ }\mathrm{score}$ for the exposed group and $\mathrm{proportion}\mathrm{ }\mathrm{unexposed}/(1-\mathrm{propensity}\mathrm{ }\mathrm{score})$ for the unexposed group. Stabilized weights should be preferred over unstabilized weights, as they tend to reduce the variance of the effect estimate [27]. It should also be noted that weights for continuous exposures always need to be stabilized [27]. As an additional measure, extreme weights may also be addressed through truncation (i.e. trimming). Weights are typically truncated at the 1st and 99th percentiles [26], although other lower thresholds can be used to reduce variance [28]. However, truncating weights change the population of inference and thus this reduction in variance comes at the cost of increasing bias [26].

After calculation of the weights, the weights can be incorporated in an outcome model (e.g. weighted linear regression for a continuous outcome or weighted Cox regression for a time-to-event outcome) to obtain estimates adjusted for confounders. IPTW estimates an average treatment effect, which is interpreted as the effect of treatment in the entire study population. Importantly, as the weighting creates a pseudopopulation containing ‘replications’ of individuals, the sample size is artificially inflated and correlation is induced within each individual. This lack of independence needs to be accounted for in order to correctly estimate the variance and confidence intervals in the effect estimates, which can be achieved by using either a robust ‘sandwich’ variance estimator or bootstrap-based methods [29].

Causal assumptions

Treatment effects obtained using IPTW may be interpreted as causal under the following assumptions: exchangeability, no misspecification of the propensity score model, positivity and consistency [30]. Exchangeability means that the exposed and unexposed groups are exchangeable; if the exposed and unexposed groups have the same characteristics, the risk of outcome would be the same had either group been exposed. Importantly, exchangeability also implies that there are no unmeasured confounders or residual confounding that imbalance the groups. In observational research, this assumption is unrealistic, as we are only able to control for what is known and measured and therefore only ‘conditional exchangeability’ can be achieved [26].

Related to the assumption of exchangeability is that the propensity score model has been correctly specified. Important confounders or interaction effects that were omitted in the propensity score model may cause an imbalance between groups. As described above, one should assess the standardized difference for all known confounders in the weighted population to check whether balance has been achieved.

The assumption of positivity holds when there are both exposed and unexposed individuals at each level of every confounder. If there are no exposed individuals at a given level of a confounder, the probability of being exposed is 0 and thus the weight cannot be defined. An almost violation of this assumption may occur when dealing with rare exposures in patient subgroups, leading to the extreme weight issues described above.

The last assumption, consistency, implies that the exposure is well defined and that any variation within the exposure would not result in a different outcome. Take, for example, socio-economic status (SES) as the exposure. SES is often composed of various elements, such as income, work and education. If we were to improve SES by increasing an individual’s income, the effect on the outcome of interest may be very different compared with improving SES through education. SES is therefore not sufficiently specific, which suggests a violation of the consistency assumption [31].

Case study—IPTW

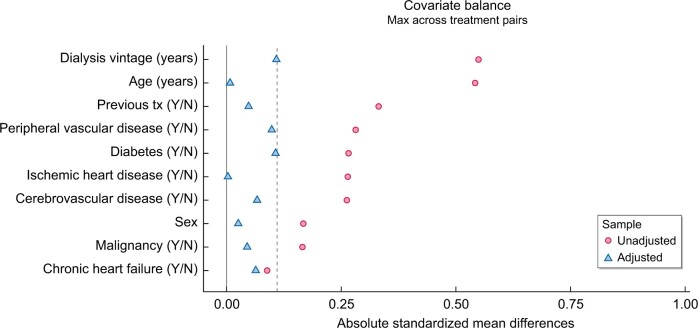
Using the propensity scores calculated in the first step, we can now calculate the inverse probability of treatment weights for each individual. Weights are calculated as $1/\mathrm{propensity}\mathrm{ }\mathrm{score}$ for patients treated with EHD and $1/(1-\mathrm{propensity}\mathrm{ }\mathrm{score})$ for the patients treated with CHD. After checking the distribution of weights in both groups, we decide to stabilize and truncate the weights at the 1st and 99th percentiles to reduce the impact of extreme weights on the variance. We then check covariate balance between the two groups by assessing the standardized differences of baseline characteristics included in the propensity score model before and after weighting. As depicted in Figure 2, all standardized differences are <0.10 and any remaining difference may be considered a negligible imbalance between groups. We can now estimate the average treatment effect of EHD on patient survival using a weighted Cox regression model.

FIGURE 2:

The standardized mean differences before (unadjusted) and after weighting (adjusted), given as absolute values, for all patient characteristics included in the propensity score model. The standardized difference compares the difference in means between groups in units of standard deviation. After adjustment, the differences between groups were <10% (dashed line), showing good covariate balance.

IPTW to account for time-dependent confounding

So far we have discussed the use of IPTW to account for confounders present at baseline. In longitudinal studies, however, exposures, confounders and outcomes are measured repeatedly in patients over time and estimating the effect of a time-updated (cumulative) exposure on an outcome of interest requires additional adjustment for time-dependent confounding. A time-dependent confounder has been defined as a covariate that changes over time and is both a risk factor for the outcome as well as for the subsequent exposure [32]. In certain cases, the value of the time-dependent confounder may also be affected by previous exposure status and therefore lies in the causal pathway between the exposure and the outcome, otherwise known as an intermediate covariate or ‘mediator’. Subsequently the time-dependent confounder can take on a dual role of both confounder and mediator (Figure 3) [33]. This situation in which the confounder affects the exposure and the exposure affects the future confounder is also known as ‘treatment-confounder feedback’. Adjusting for time-dependent confounders using conventional methods, such as time-dependent Cox regression, often fails in these circumstances, as adjusting for time-dependent confounders affected by past exposure (i.e. in the role of mediator) may inappropriately block the effect of the past exposure on the outcome (i.e. overadjustment bias) [32]. For example, we wish to determine the effect of blood pressure measured over time (as our time-varying exposure) on the risk of end-stage kidney disease (ESKD) (outcome of interest), adjusted for eGFR measured over time (time-dependent confounder). As eGFR acts as both a mediator in the pathway between previous blood pressure measurement and ESKD risk, as well as a true time-dependent confounder in the association between blood pressure and ESKD, simply adding eGFR to the model will both correct for the confounding effect of eGFR as well as bias the effect of blood pressure on ESKD risk (i.e. inappropriately block the effect of previous blood pressure measurements on ESKD risk).

FIGURE 3:

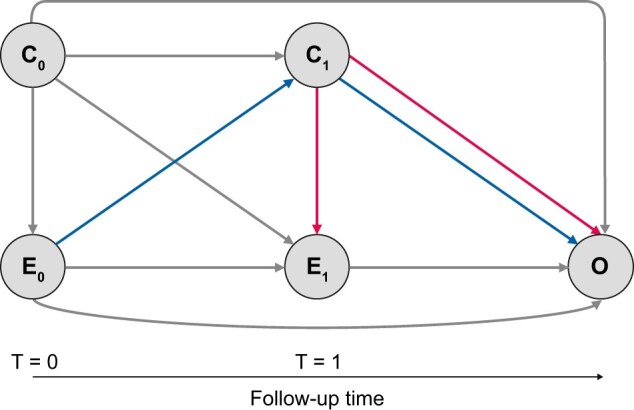
Directed acyclic graph depicting the association between the cumulative exposure measured at t = 0 (E₀) and t = 1 (E₁) on the outcome (O), adjusted for baseline confounders (C₀) and a time-dependent confounder (C₁) measured at t = 1. The time-dependent confounder (C₁) in this diagram is a true confounder (pathways given in red), as it forms both a risk factor for the outcome (O) as well as for the subsequent exposure (E₁). However, the time-dependent confounder (C₁) also plays the dual role of mediator (pathways given in purple), as it is affected by the previous exposure status (E₀) and therefore lies in the causal pathway between the exposure (E₀) and the outcome (O). This situation in which the exposure (E₀) affects the future confounder (C₁) and the confounder (C₁) affects the exposure (E₁) is known as treatment-confounder feedback. In this situation, adjusting for the time-dependent confounder (C₁) as a mediator may inappropriately block the effect of the past exposure (E₀) on the outcome (O), necessitating the use of weighting.

An additional issue that can arise when adjusting for time-dependent confounders in the causal pathway is that of collider stratification bias, a type of selection bias. This type of bias occurs in the presence of an unmeasured variable that is a common cause of both the time-dependent confounder and the outcome [34]. Controlling for the time-dependent confounder will open a non-causal (i.e. spurious) path between the unobserved variable and the exposure, biasing the effect estimate. An illustrative example of collider stratification bias, using the obesity paradox, is given by Jager et al. [34]. The obesity paradox is the counterintuitive finding that obesity is associated with improved survival in various chronic diseases, and has several possible explanations, one of which is collider-stratification bias. In this example, the association between obesity and mortality is restricted to the ESKD population. In this case, ESKD is a collider, as it is a common cause of both the exposure (obesity) and various unmeasured risk factors (i.e. lifestyle factors). Restricting the analysis to ESKD patients will therefore induce collider stratification bias by introducing a non-causal association between obesity and the unmeasured risk factors. As a consequence, the association between obesity and mortality will be distorted by the unmeasured risk factors.

Under these circumstances, IPTW can be applied to appropriately estimate the parameters of a marginal structural model (MSM) and adjust for confounding measured over time [35, 36]. As weights are used (i.e. a marginal approach), as opposed to regression adjustment (i.e. a conditional approach), they do not suffer from these biases. Unlike the procedure followed for baseline confounders, which calculates a single weight to account for baseline characteristics, a separate weight is calculated for each measurement at each time point individually. To achieve this, the weights are calculated at each time point as the inverse probability of being exposed, given the previous exposure status, the previous values of the time-dependent confounder and the baseline confounders. This creates a pseudopopulation in which covariate balance between groups is achieved over time and ensures that the exposure status is no longer affected by previous exposure nor confounders, alleviating the issues described above. Extreme weights can be dealt with as described previously. For the stabilized weights, the numerator is now calculated as the probability of being exposed, given the previous exposure status, and the baseline confounders. Although including baseline confounders in the numerator may help stabilize the weights, they are not necessarily required. If the choice is made to include baseline confounders in the numerator, they should also be included in the outcome model [26]. After establishing that covariate balance has been achieved over time, effect estimates can be estimated using an appropriate model, treating each measurement, together with its respective weight, as separate observations. This type of weighted model in which time-dependent confounding is controlled for is referred to as an MSM and is relatively easy to implement. For instance, a marginal structural Cox regression model is simply a Cox model using the weights as calculated in the procedure described above.

Inverse probability of censoring weighting to account for informative censoring

In time-to-event analyses, patients are censored when they are either lost to follow-up or when they reach the end of the study period without having encountered the event (i.e. administrative censoring). Methods developed for the analysis of survival data, such as Cox regression, assume that the reasons for censoring are unrelated to the event of interest. In the case of administrative censoring, for instance, this is likely to be true. In other cases, however, the censoring mechanism may be directly related to certain patient characteristics [37]. For instance, patients with a poorer health status will be more likely to drop out of the study prematurely, biasing the results towards the healthier survivors (i.e. selection bias). As these censored patients are no longer able to encounter the event, this will lead to fewer events and thus an overestimated survival probability. Similar to the methods described above, weighting can also be applied to account for this ‘informative censoring’ by up-weighting those remaining in the study, who have similar characteristics to those who were censored. To achieve this, inverse probability of censoring weights (IPCWs) are calculated for each time point as the inverse probability of remaining in the study up to the current time point, given the previous exposure, and patient characteristics related to censoring. In situations where inverse probability of treatment weights was also estimated, these can simply be multiplied with the censoring weights to attain a single weight for inclusion in the model. An illustrative example of how IPCW can be applied to account for informative censoring is given by the Evaluation of Cinacalcet Hydrochloride Therapy to Lower Cardiovascular Events trial, where individuals were artificially censored (inducing informative censoring) with the goal of estimating per protocol effects [38, 39].

Advantages and limitations of IPTW

IPTW has several advantages over other methods used to control for confounding, such as multivariable regression. The propensity score–based methods, in general, are able to summarize all patient characteristics to a single covariate (the propensity score) and may be viewed as a data reduction technique. These methods are therefore warranted in analyses with either a large number of confounders or a small number of events. IPTW also has some advantages over other propensity score–based methods. Compared with propensity score matching, in which unmatched individuals are often discarded from the analysis, IPTW is able to retain most individuals in the analysis, increasing the effective sample size. In addition, whereas matching generally compares a single treatment group with a control group, IPTW can be applied in settings with categorical or continuous exposures. Furthermore, compared with propensity score stratification or adjustment using the propensity score, IPTW has been shown to estimate hazard ratios with less bias [40]. In the longitudinal study setting, as described above, the main strength of MSMs is their ability to appropriately correct for time-dependent confounders in the setting of treatment-confounder feedback, as opposed to the potential biases introduced by simply adjusting for confounders in a regression model.

IPTW also has limitations. Some simulation studies have demonstrated that depending on the setting, propensity score–based methods such as IPTW perform no better than multivariable regression, and others have cautioned against the use of IPTW in studies with sample sizes of <150 due to underestimation of the variance (i.e. standard error, confidence interval and P-values) of effect estimates [41, 42]. The IPTW is also sensitive to misspecifications of the propensity score model, as omission of interaction effects or misspecification of functional forms of included covariates may induce imbalanced groups, biasing the effect estimate.

CONCLUSION

Conceptually analogous to what RCTs achieve through randomization in interventional studies, IPTW provides an intuitive approach in observational research for dealing with imbalances between exposed and non-exposed groups with regards to baseline characteristics. After careful consideration of the covariates to be included in the propensity score model, and appropriate treatment of any extreme weights, IPTW offers a fairly straightforward analysis approach in observational studies. Moreover, the weighting procedure can readily be extended to longitudinal studies suffering from both time-dependent confounding and informative censoring.

CONFLICT OF INTEREST STATEMENT

None declared.