Figure 1. LD and finite GWAS sample size introduce uncertainty into PRS estimation.

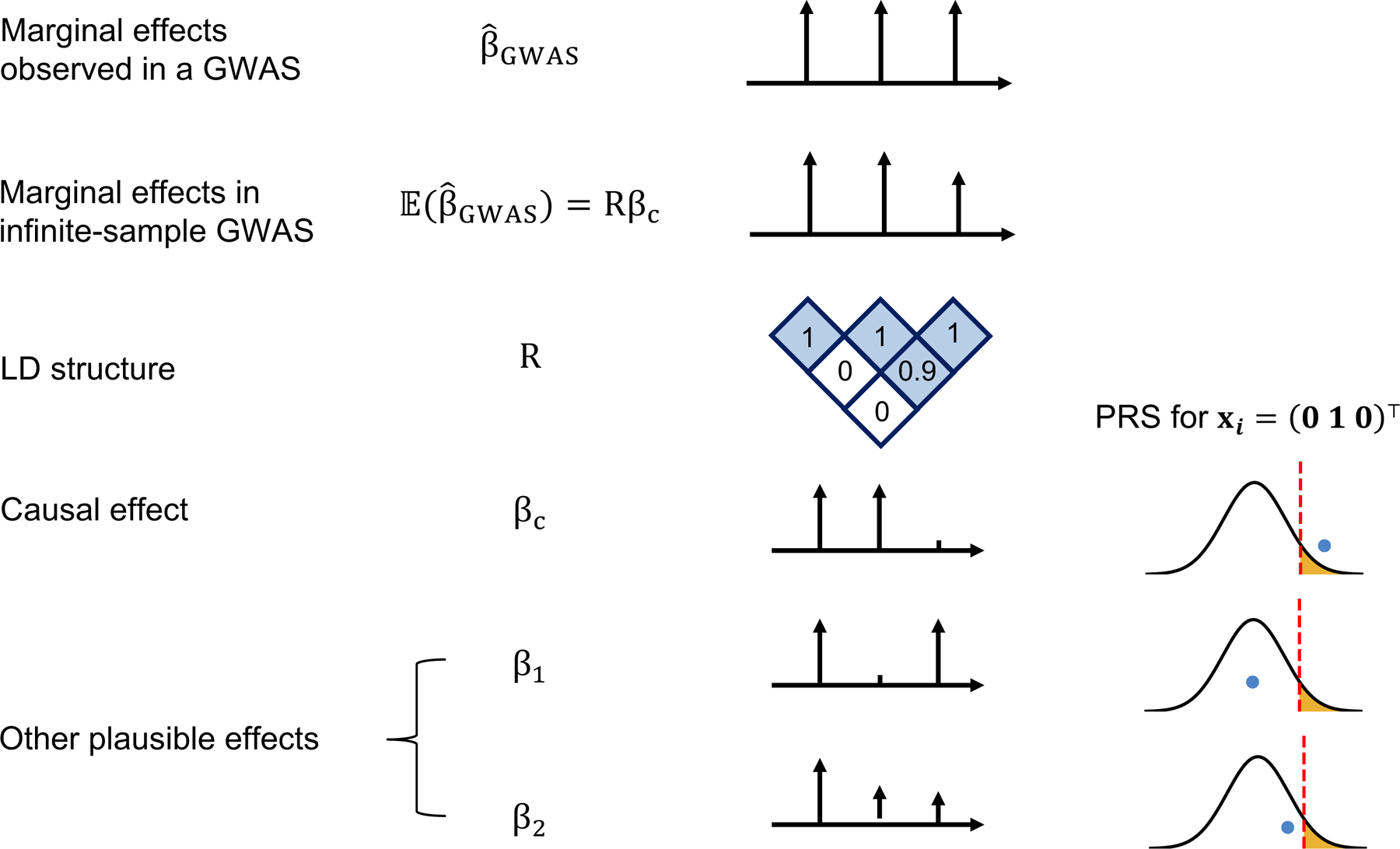
We simulated a GWAS of N individuals across 3 SNPs with LD structure R (SNP2 and SNP3 are in LD of 0.9 whereas SNP1 is uncorrelated to other SNPs) where SNP1 and SNP2 are causal with the same effect size β_c = (0.016, 0.016, 0) such that the variance explained by this region is var(x^⊤β_c) = 0.5/1000 corresponding to a trait with total heritability of 0.5 uniformly distributed across 1,000 causal regions. The marginal effects observed in a GWAS, ${\widehat{\beta }}_{\text{GWAS}}$, have an expectation of Rβ_c and variance-covariance $\left({\sigma }_{\text{e}}^2/\text{N}\right)R$, thus showcasing the statistical noise introduced by finite sample size of GWAS (N); for example, the probability of the marginal GWAS effect at tag SNP3 to exceed the marginal effect of true causal SNP2, although decreases with N, remains considerably high for realistic sample and effect sizes (12% at N=100,000 for a trait with h2=0.5 split across 1,000 causal regions, see Supplementary Figure 1). We consider one such observation for the effects observed in a GWAS: ${\widehat{\beta }}_{\text{GWAS}}=\left(0.016,0.016,0.016\right)$. Given such observation, in addition to the true causal effects (β_c), other causal configurations are probable β₁=(0.016, 0, 0.016) or β₂=(0.016, 0.008, 0.008). An individual with genotype x_i = (0 1 0)^⊤ will attain different PRS estimates under these different causal configurations. Most importantly, in the absence of other prior information, β₁ and β_c are equally probable given the data thus leading to different PRS estimates for individual x_i = (0 1 0)^⊤.