Table A2.

Explanation of different methods for estimating the relationship between animal AMU and human AMR at the population level.

Method	Description	Data Requirement	Reference Examples for the Case of AMU and AMR
Transmission dynamic mathematical models	Can take a number of forms; including individual-based models, difference equation models, and differential equation models. These simulation models attempt to track important OH sub-populations, their resistance carriage and antibiotic exposure, with transmission rates dependent on current prevalence (dynamic)	Inputs: antibiotic exposure, population sizes, infection rates To fit to: prevalence of AMR (colonising or infecting) over time for each sub-population. This can be used to infer transmission parameters and selection rates (per antimicrobial) exposure)	$$\begin{gathered} \frac{\delta H}{\delta t}=\gamma {\mathsf{\Lambda }}_H\left(1-H\right)+{\mathsf{\Lambda }}_H{\beta }_{HH}H\left(1-H\right)+{\mathsf{\Lambda }}_H{\beta }_{\mathsf{\Lambda }H}A\left(1-H\right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\mathsf{\Lambda }}_H{\beta }_{EH}E\left(1-H\right)-{\mu }_{H}H \end{gathered}$$ (Booton et al., 2021) [21] A single equation from this model of Thailand where t is time; H, A, and E are resistance prevalence in different sub-populations; xy is the transmission of resistance between sub-populations x and y; ΛH is human AMU; γ is the speed at which humans and animals are colonised by resistant bacteria; and μH is the natural rate of decay of resistance in humans
Decision-analytic hierarchical models	The prevalence of AMR in infections in humans is a specified function of a range of factors across the various OH compartments, which in turn are functions of other factors	Actual or approximate values for all of the parameters used across the three OH compartments: human (e.g., incidence of raw meat consumption), animal (e.g., prevalence of biosecurity measures in farms), and environment (e.g., prevalence of good manufacturing practices). AMR surveillance data for external validation
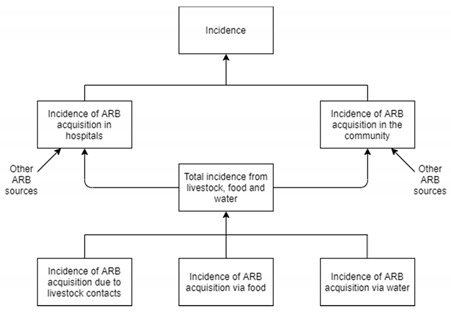
			(Opatowski et al., 2020) [61] The risk of human AMR acquisition in a representative Asian population is modelled using this multi-level causal model
Panel regression models	Data on AMR and AMU in humans and food-producing animals, as well as other relevant covariates, are collected over time and for multiple geographical units (e.g., countries or administrative areas). Human AMR is regressed against these covariates using a method such as fixed effects (static) or system GMM (dynamic)	Country-level surveillance data on AMR and AMU in humans and food-producing animals over time, as well as country-level data on appropriate controls, e.g., medical staffing, portion of employment in agriculture, population density, average annual temperature, and income per capita	$$\begin{gathered} lnAM{R}_{i,t}={\beta }_0+{\beta }_{1}lnM{S}_{i,t}+{\beta }_{2}lnV{P}_{i,t}+{\beta }_{3}lnHAM{C}_{i,t} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\beta }_{4}lnVAM{C}_{i,t}+u_i+{\theta }_t+{\epsilon }_{i,t} \end{gathered}$$ (Zhang, Cui and Zhang, 2018) [56] Where lnAMR is log AMR prevalence in humans, i denotes country and t denotes year; MS denotes the number of medical staff and VP denotes the number of veterinary professionals; and VAMC and HAMC denote veterinary and human antimicrobial consumption Fluoroquinolone resistance in E. coli and P. aeruginosa is regressed against a series of country-level factors for a panel of European countries